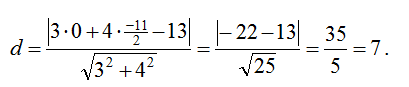Как найти площадь квадрата лежащего на прямых

Две стороны квадрата лежат на прямых 3x+4y+22=0 и 3x+4y-13=0. Вычислить его площадь.

Решение

Из заданных уравнений прямых следует, что они параллельны (коэффициенты A и B – одинаковы). Для нахождения длины стороны квадрата нужно найти расстояние от одной прямой до другой. Это можно сделать, взяв точку на одной прямой и определить расстояние от нее до другой прямой.

Возьмем первую прямую:

3x+4y+22=0, пусть x=0, подставив это значение в уравнение, получим уравнение относительно y, откуда найдем

Таким образом, получим точку, принадлежащую первой прямой:

Расстояние от точки с известными координатами до прямой определяем с помощью формулы:

Теперь определяем площадь:

Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Источник

Ученик

(166),
закрыт

12 лет назад

Татьяна

Просветленный

(40515)

12 лет назад

Поскольку данные прямые параллельны, то сторону квадрата можно найти как расстояние от произвольной точки одной прямой до другой прямой.
Найдем какую-нибудь точку на первой прямой. Пусть, например, х=1. тогда 1+2у+5=0, откуда у=-3. Теперь найдем расстояние от точки (1;-3) до прямой х+2у+3=0.
d=(|1*1+2*(-3)+3|)/V(1^2+2^2)=2/V5.
S квадрата=(2/V5)^2=4/5.

Карен Мартиросян

Гуру

(3668)

12 лет назад

Заметим, что условие задачи выполнимо лишь в случае, когда прямые параллельны (если прямые перпендикулярны, то квадрат не определён, а если пересекаются под острым углом, то квадрат не существует). Убедимся, что прямые параллельны. Уравнения прямых запишем в виде: (1) у = – 0,5х – 2,5 ;
(2) у = – 0,5х – 1,5. Действительно, прямые параллельны (угловые коэффициенты равны, свободные члены – нет). Сторона квадрата равна расстоянию между этими прямыми. На (1)-ой прямой возьмём произвольную точку: при х=1 ==> у=-3. Пусть прямая у = кх + в проходит через точку М (1;-3) и перпендикулярна прямой (2).
Тогда произведение их угловых коэффициентов = -1 (условие перпендикулярности двух прямых) : -0,5к = -1
к = 2. Т. к. точка М (1;-3) принадлежит прямой у=кх+в, то -3=2*1 + в, откуда в = -5. Таким образом, прямая
у=2х-5 проходит через точку М и перпендикулярна прямой (2).Найдём точку их пересечения:
2х-5=-0,5х-1,5 ; х=1,4 ==> у= -2,2. И так, точка пересечения: N(1,4 ; -2,2) Сторона квадрата равна отрезку MN.
MN^ =(1,4-1)^ + (-2,2+3)^ = 0,16 + 0,64 = 0,8. Sквадрат. = 0,8.

Источник

Светило науки – 9969 ответов – 46531 помощь

Найти расстояние между прямыми L1 и L2

L1: 6 x −4 y −12 =0 (1)

L2: 12 x −8 y + 16 =0 (2)

Решение.

Прямая L1 имеет свободный член C1=-12 и направляющий вектор

n1={A1, B1}={6, −4}

Прямая L2 имеет свободный член C2=16 и направляющий вектор

n2={A2, B2}={12, −8}

Уравнение прямой L2 не изменится, если его умножим на число 6/12.

L2: 6 x −4 y + 8 = 0 (2′)

Теперь, нормальный вектор прямой L2 равен n2={A2, B2}={6, −4}, а свободный член: C2=8.

Так как нормальные векторы прямых L1 и L2 совпадают, то расстояние между ними можно вычислить формулой:

d=|C1−C2|/√(A1² + B1²) (3)

Подставим значения A1, B1, C1, C2 в (3):

d=|−12−8|/√(6)²+(−4)²= 20/ √52 = 10/ √13 = 2,774. (4)

Расстояние между прямыми равно:

d= 2,774.

Это расстояние равно длине стороны квадрата.

Тогда площадь квадрата равна:

S = (10/ √13)² = 100/13 ≈ 7,69231 кв. ед.

Источник

Задать свой вопрос

*более 50 000 пользователей получили ответ на «Решим всё»

Задача 32546 найдите площадь квадрата стороны…

Условие

vk448340035

2019-01-05 12:14:17

найдите площадь квадрата стороны которого лежат на прямых 3х-4у+10=0 и 6х-8у-13=0

математика ВУЗ
922

Решение

sova

2019-01-05 15:10:44

★

Прямые параллельны.
3x-4y+10=0
3x-4y-6,5=0

d=|C_(2) – C_(1)|/sqrt(A^2+B^2)=| – 6,5 -10|/sqrt(3^2+(-4)^2)=16,5/5=3,1

a(квадрата)=d

S(квадрата)=a^2=3,1^2=9,61

Написать комментарий

Присоединяйся в ВК

Источник

Сообщение было отмечено Royal_X как решение

Решение

На прямой берем любую точку, например, точку .

Далее, ищем расстоянии от точки до прямой .

$https://www.cyberforum.ru/cgi-bin/latex.cgi?d = frac{left|a {P}_{x}+b {P}_{y}+c right|}{sqrt{{a}^{2}+{b}^{2}}}=frac{left|3cdot (-1)+2 cdot 1+(-6) right|}{sqrt{{3}^{2}+{2}^{2}}}=frac{7}{sqrt{13}}=frac{7sqrt{13}}{13}approx 1,94145$

Находим площадь квадрата:

$https://www.cyberforum.ru/cgi-bin/latex.cgi?S = {d}^{2} = 49/13 approx 3,76923$

Но есть еще одна интересная формула, по которой можно вычислить расстоянии между двумя параллельными прямыми:

Допустим есть параллельные прямые $https://www.cyberforum.ru/cgi-bin/latex.cgi?ax+by+{c}_{1}=0$ и $https://www.cyberforum.ru/cgi-bin/latex.cgi?ax+by+{c}_{2}=0$ . Тогда расстояние между ними равно:

$https://www.cyberforum.ru/cgi-bin/latex.cgi?d = frac{left|{c}_{2}-{c}_{1} right|}{sqrt{{a}^{2}+{b}^{2}}}$

В нашем случае это будет так:

$https://www.cyberforum.ru/cgi-bin/latex.cgi?d = frac{left|1-(-6) right|}{sqrt{{3}^{2}+{2}^{2}}}=frac{7}{sqrt{13}}=frac{7sqrt{13}}{13}$

Как видно, эта формула лучше, чем предыдущая, для которой мы должны потратить время еще для поиска точки.

Источник