Расчёт площади квадрата по радиусу описанной окружности
Калькулятор рассчитывает площадь квадрата по радиусу описанной окружности.
Формула площади квадрата по радиусу описанной окружности
Где S – площадь квадрата,
R – радиус описанной окружности
Вывод формулы площади квадрата по радиусу описанной окружности

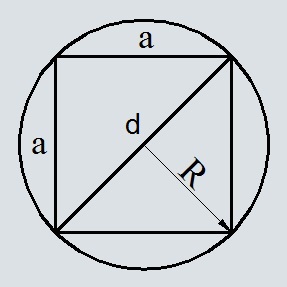
Диагональ квадрата равна диаметру окружности или двум радиусам
С помощью теоремы Пифагора выведем сторону a через диагональ
Подставим в формулу площади квадрата
Диагональ квадрата равна диаметру окружности или двум радиусам
Подставим и выведем формулу
Похожие калькуляторы

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону

S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ

S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности

S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности

S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр

S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Как определить площадь квадрата

О чем эта статья:
3 класс, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a 2 , где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d 2 : 2, где d — диагональ.
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r 2 , где r — это радиус вписанной окружности.
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R 2 , где R — это радиус описанной окружности.
У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р 2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Воспользуемся формулой: S = d 2 : 2.
Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .
Ответ: 4050 мм 2 .
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d
Диаметр окружности равен двум радиусам:
d = 2r
Получается, что сторона равна двум радиусам:
a = 2r
Используем формулу нахождения площади квадрата через сторону:
S = a 2
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2
Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2
Онлайн калькулятор площади вписанного в круг квадрата. Как узнать площадь вписанного в круг квадрата.






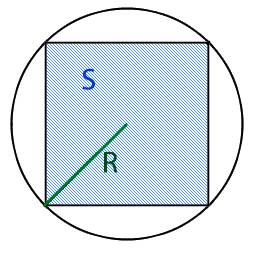
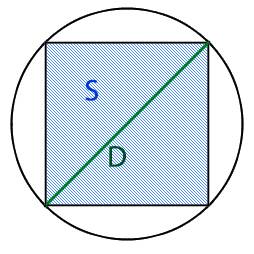
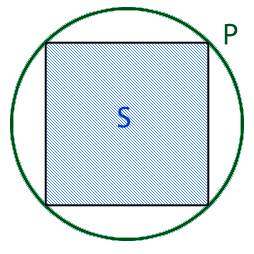
Вычислить площадь вписанного квадрата через:
Радиус круга R:
Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
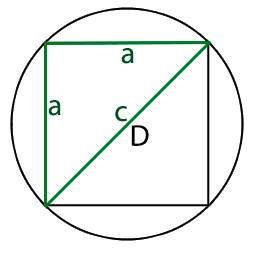
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
мы можем узнать длину сторон квадрата используя теорему Пифагора
после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.
Как найти площадь квадрата
Как найти площадь квадрата?
Площадь квадрата может быть найдена по его стороне, диагонали, радиусам вписанной и описанной окружности.
1. Площадь квадрата равна квадрату его стороны.
Формула для нахождения площади квадрата по его стороне:
Например, площадь квадрата ABCD можно найти как квадрат его стороны AB:
2. Площадь квадрата равна половине квадрата диагонали его стороны.
Формула для нахождения площади квадрата по его диагонали:
Например, площадь квадрата ABCD можно найти через его диагональ AC:
3. Площадь квадрата в четыре раза больше квадрата радиуса вписанной к него окружности.
Так как
то из формулы площади квадрата по стороне получаем
формулу для нахождения площади квадрата через радиус вписанной окружности:
4. Площадь квадрата равна удвоенному квадрату радиуса описанной около него окружности.
Так как
то из формулы площади квадрата по стороне вытекает
формула для нахождения площади квадрата через радиус вписанной окружности:
[spoiler title=”источники:”]
http://tamali.net/calculator/inscribed/square/area/
[/spoiler]
При помощи нашего калькулятора вы легко сможете узнать площадь квадрата описанного около окружности.
Для того, что бы узнать площадь квадрата описанного около окружности необходимо с тем что у этих двух фигур общее, а одной из общих величин у них является сторона квадрата которая равна диаметру круга.
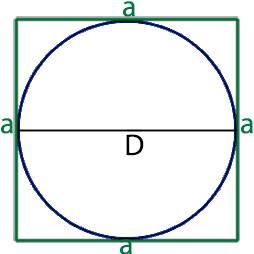
a=D
Таким образом для нахождения площади квадрата описанного около окружности, через этот круг, необходимо найти значение диаметра.
Для нахождения диаметра окружности нам необходимо знать одну из его величин а именно:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=P/π
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=2R
Соответственно если мы знаем диаметр круга который равен стороне описанного квадрата,
a=D
Теперь мы можем узнать площадь этого квадрата
p = a2
Площадь квадрата онлайн
С помощю этого онлайн калькулятора можно найти площадь квадрата. Для нахождения площади квадрата, введите известные данные в ячейку и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Площадь квадрата. Определение
Определение 1. Площадь квадрата − это величина той части плоскости, которую занимает квадрат.
Единицы измерения площади квадрата
За единицу измерения площадей применяют квадрат, сторона которого равна единице измерения отрезков. В качестве единицы измерения площадей принимают квадраты со сторонами 1мм, 1см, 1дм, 1м и т.д (Рис.1). Такие квадраты назыают квадратным миллиметром, квадратным сантиметром, квадратным дециметром, квадратным метром и т.д., соответственно. Обозначаются они мм2, см2, дм2, м2 и т.д., соответственно.
Если выбрана единица измерения, то площадь измеряемого объекта (квадрата, треугольника, прямоугольника, многоугольника и т.д.)определяется положительным числом, которая определяет сколько раз единица измерения и ее части укладываются в данном объекте.
Для измерения отдельных плоских фигур используются специальные формулы. В данной статье мы выведем формулу для вычисления площади квадрата.
Площадь квадрата. Доказательство
Теорема 1. Площадь S квадрата со стороной a равна 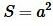 .
.
Доказательство. Пусть n целое неотрицательное число и пусть 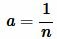 . Рассмотрим квадрат со стороной 1 (Рис.2). Разделим этот квадрат по ветрикали и по горизонлали на n равных частей. Получим
. Рассмотрим квадрат со стороной 1 (Рис.2). Разделим этот квадрат по ветрикали и по горизонлали на n равных частей. Получим 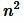 маленьких квадратов состоронами
маленьких квадратов состоронами 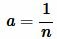 . Поскольку площадь большого квадрата равна 1 (так как является единицей измерения), то очевидно, что площадь маленького квадрата равна:
. Поскольку площадь большого квадрата равна 1 (так как является единицей измерения), то очевидно, что площадь маленького квадрата равна:
а поскольку 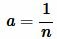 , то имеем:
, то имеем:
Пусть теперь a является конечной десятичной дробью, содержащую n знаков после запятой. (Если n=0, то a будет целым числом). Тогда a можно представить в виде обыкновенной дроби, умножив и делив на 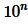 :
:
откуда
где m − целое число.
Возьмем квадрат со стороной a и разделим его по горизонлали и вертикали на m ровных частей. Получим m2 маленьких квадратов (Рис.3).
Тогда, учитывая (2), сторона каждого квадрата равна:
По формуле (1) площадь маленького квадрата равна:
Следовательно, площадь квадрата со стороной a равна:
Пусть, далее, число a представляет собой бесконечную десятичную дробь. Рассмотрим число an которая получается из a отбрасыванием всех десятичных знаков после запятой, начиная с (n+1)-го. Поскольку a отличается от an не более, чем на 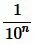 , то имеем:
, то имеем:
откуда
Из неравенства (4) следует, что площадь S квадрата со стороной a заключена между площадью квадрата со стороной an и площадью квадрата со стороной 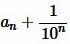 (Рис.4), т.е.
(Рис.4), т.е.
При неограниченном увеличении числа n, число 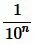 будет становиться сколь угодно малым и, следовательно, число
будет становиться сколь угодно малым и, следовательно, число 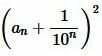 будет сколь угодно мало отличаться от
будет сколь угодно мало отличаться от 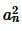 . Тогда из неравенства (5) следует, что число S будет мало отличаться от числа
. Тогда из неравенства (5) следует, что число S будет мало отличаться от числа 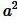 . Следовательно они равны, т.е.
. Следовательно они равны, т.е. 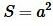 .
.
Площадь квадрата по стороне
Из вышеизложенного доказательства получили, что площадь квадрата равна:
где ( small a ) сторона квадрата.
Пример 1. Сторона квадрата равна 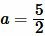 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (6). Подставляя 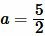 в (6), получим:
в (6), получим:
Ответ: 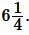
Площадь квадрата по диагонали
Пусть известна диагональ ( small d ) квадрата (Рис.5). Найдем площадь квадрата.
Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Для этого воспользуемся теоремой Пифагора:
Подставляя (7) в (6), получим:
то есть площадь квадрата по диагонали вычисляется из следующей формулы:
Пример 2. Диагональ квадрата равна 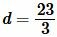 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (8). Подставляя 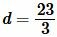 в (8), получим:
в (8), получим:
Ответ: 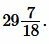
Площадь квадрата по радиусу вписанной окружности
Пусть известен ( small r ) радиус окружности вписанной в квадрат (Рис.6). Найдем площадь квадрата.
Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Нетрудно заметить, что радиус ( small r ) равна половине стороны ( small a ) квадрата, т.е.
Подставляя (9) в (6), получим:
или
Пример 3. Радиус вписанной в квадрат окружности равен 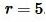 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (10). Подставляя 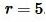 в (10), получим:
в (10), получим:
Ответ: 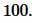
Площадь квадрата по радиусу описанной окружности
Пусть известен ( small R ) радиус окружности описанной около квадрата (Рис.7). Найдем площадь квадрата.
Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Восрользуемся теоремой Пифагора:
Подставляя (11) в (6), получим:
Пример 4. Радиус описанной окружности равен 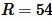 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения площади квадрата воспользуемся формулой (12). Подставляя 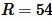 в (12), получим:
в (12), получим:
Ответ: 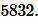
Площадь квадрата по периметру
Пусть известен периметр ( small P ) квадрата. Найдем площадь квадрата. По периметру можно найти сторону квадрата:
Подставляя (13) в (6), получим:
то есть площадь квадрата через периметр равна:
Пример 5. Периметр квадрата равен 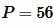 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения площади квадрата воспользуемся формулой (14). Подставляя 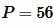 в (14), получим:
в (14), получим:
Ответ: 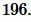
Смотрите также:
- Квадрат. Онлайн калькулятор
