Как найти площадь квадрата при помощи диагонали - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Наиболее распространенной формулой для вычисления площади квадрата является следующая: S = a². Но иногда в задаче дана только диагональ квадрата, то есть отрезок, соединяющий противоположные вершины. Если вы знакомы с прямоугольными треугольниками, для вычисления площади квадрата можно воспользоваться формулой, которая включает диагональ.

1

Нарисуйте квадрат. У квадрата четыре равные стороны.^[1] Допустим, что длина каждой стороны равна а.
2

Посмотрите на основную формулу для вычисления площади квадрата. Площадь квадрата равна произведению длины на ширину. Так как каждая сторона квадрата равна а, формула для вычисления площади квадрата: S = а х а = а². Эта формула понадобится далее.
3

Соедините два противоположных угла квадрата, чтобы провести диагональ. Допустим, что длина диагонали равна d. Диагональ делит квадрат на два прямоугольных треугольника.
4
К одному из треугольников примените теорему Пифагора. По теореме Пифагора^[2] можно найти гипотенузу (самую длинную сторону) прямоугольного треугольника: $a^{2}+b^{2}=c^{2}$ , где а и b — катеты, с — гипотенуза. Разделив квадрат на два прямоугольных треугольника, примените эту формулу к одному из них.
- Катетами прямоугольного треугольника являются стороны квадрата, каждая из которых равна а.
- Гипотенузой является диагональ квадрата, равная d.
- $a^{2}+a^{2}=d^{2}$
5
6

Воспользуйтесь этой формулой для решения задачи. Полученную формулу S = ${frac {d^{2}}{2}}$ можно применять к любым квадратам: просто подставьте в нее значение диагонали (вместо d).

Реклама

1

Найдите диагональ по стороне.^[3] Если сторона квадрата равна а, а диагональ равна d, теорема Пифагора запишется так: $2a^{2}=d^{2}$ . По этой формуле можно вычислить диагональ, если сторона квадрата известна.
2
3
Проверьте правильность формулы. Верность математического вывода формулы S = ${frac {d^{2}}{2}}$ не вызывает сомнений, но можно ли проверить правильность формулы наглядно? Допустим, что сторона второго квадрата равна d, то есть диагонали первого квадрата; тогда площадь второго квадрата равна $d^{2}$ . Так как формула для вычисления площади S = ${frac {d^{2}}{2}}$ , можно заключить, что площадь второго квадрата в два раза больше площади первого квадрата. Проверьте это наглядно:
- На бумаге нарисуйте первый квадрат. Убедитесь, что все стороны равны.
- Измерьте диагональ. Нарисуйте второй квадрат: каждая его сторона должна быть равна диагонали первого квадрата.
- Нарисуйте копию первого квадрата, а затем вырежьте три квадрата.
- Разрежьте два меньших квадрата так, чтобы они поместились в большем квадрате. Два меньших квадрата должны полностью покрыть больший квадрат, что доказывает, что площадь большего квадрата в два раза больше площади меньшего квадрата.
Реклама

Советы

Если калькулятора нет, но необходимо получить точное значение √2, извлеките корень вручную. Например, примените метод Ньютона-Рафсона.^[4]
Приведенная формула используется во многих областях, в том числе в кристаллографии, химии и технике. Например, при помощи этой формулы можно вычислить площадь ландшафта, который виден воочию или на фотографии/рисунке. Для этого измерьте пройденный путь, а затем проведите воображаемую диагональ.
Если вы предпочитаете изучать математику с наглядными примерами или хотите узнать, как использовать диаграммы и графики в искусстве, читайте статьи на сайте wikiHow (например, в категориях «Математика», «Графические программы», «Офисные программы» и других).

Об этой статье

Эту страницу просматривали 50 355 раз.

Была ли эта статья полезной?

Источник

Площадь квадрата (по диагонали): онлайн-калькулятор

Квадрат – это правильный четырёхугольник, у которого все стороны и углы равны. У квадрата две диагонали, соединяющие несмежные вершины фигуры. Расчет площади квадрата по диагонали онлайн-калькулятором производится по формуле S=12*d2, где d – диагональ квадрата

Чтобы найти площадь квадрата по диагонали онлайн, понадобится несколько простых действий:

указать размер диагонали и единицы измерения;
выбрать, в каких единицах необходимо рассчитать площадь;
получить ответ после нажатия на кнопку «Найти».

Вычисление площади квадрата по диагонали онлайн

При отсутствии данных о длине стороны квадрата можно найти площадь фигуры другим способом. В данном случае можно не прибегать к услугам программных средств и все действия произвести самостоятельно. Но если величина диагонали содержит несколько знаков, то при возведении ее в квадрат есть вероятность допустить ошибку.

Рассчитать площадь квадрата по диагонали онлайн понадобится:

школьникам, которые выполняют домашнее задание по геометрии;
родителям для быстрого контроля;
учителям, проверяющим работы класса;
студентам, которым важен точный ответ, на который опираются дальнейшие вычисления.

Сервис выдает последовательное решение задачи с точным ответом. С помощью сайта Zaochnik можно осуществлять подготовку к занятиям без привлечения репетиторов, траты средств и лишнего времени.

Источник

{S = a ^2}

На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.

Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.

Содержание:

калькулятор площади квадрата
формула площади квадрата через сторону
формула площади квадрата через диагональ
формула площади квадрата через радиус вписанной окружности
формула площади квадрата через радиус описанной окружности
формула площади квадрата через периметр
примеры задач

Формула площади квадрата через сторону

S = a ^2

a – сторона квадрата

Формула площади квадрата через диагональ

S=dfrac{d^2}{2}

d – диагональ квадрата

Формула площади квадрата через радиус вписанной окружности

S = 4r^2

r – радиус вписанной окружности

Формула площади квадрата через радиус описанной окружности

S = 2R^2

R – радиус описанной окружности

Формула площади квадрата через периметр

S = dfrac{P^2}{16}

P – периметр квадрата

Примеры задач на нахождение площади квадрата

Задача 1

Найдите площадь квадрата если его диагональ равна 1.

Решение

Для решения задачи воспользуемся формулой.

S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2

Ответ: 0.5 см²

Проверим ответ на калькуляторе .

Задача 2

Найдите площадь квадрата, описанного вокруг окружности радиуса 83.

Решение

Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.

S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2

Ответ: 13778 см²

Проверим ответ с помощью калькулятора .

Задача 3

Найдите площадь квадрата если его сторона равна 8 см.

Решение

Используем первую формулу.

S = a ^2 = 8 ^2 = 64 : см^2

Ответ: 64 см²

Проверим результат на калькуляторе .

Задача 4

Найдите площадь квадрата периметр которого равен 456 см.

Решение

Используем формулу для площади квадрата через периметр.

S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2

Ответ: 12996 см²

Проверка .

Задача 5

Найдите площадь квадрата со стороной 15 см.

Решение

Воспользуемся формулой площади квадрата через сторону.

S = a ^2 = 15 ^2 = 225 : см^2

Ответ: 225 см²

Проверка .

Источник

Download Article

The most common formula for the area of a square is simple: it’s the length of the side squared, or s².^[1] But sometimes you only know the length of the square’s diagonal, running between opposite vertices. If you’ve studied right triangles, you can find a new area formula that uses this diagonal as its only variable.

1

Draw your square. A square has four equal sides.^[2] Let’s say each one has a length of “s”.
2

Review the basic formula for a square’s area. A square’s area is equal to its length times its width. Since each side is s, the formula is Area = s x s = s². This will be useful later on.^[3]

Advertisement
3

Join any two opposite corners to make a diagonal. Let the measure of this diagonal be d units. This diagonal divides the square into two right-triangles.
4
Apply the Pythagorean Theorem to one of the triangles. The Pythagorean theorem^[4] is a formula for finding the hypotenuse (longest side) of a right triangle: (side one)² + (side two)² = (hypotenuse)², or $a^{2}+b^{2}=c^{2}$ . Now that the square is divided in half, you can use this formula on one of the right triangles:
- The two shorter sides of the triangle are the sides of the square: each one has a length of s.
- The hypotenuse is the diagonal of the square, d.
- $s^{2}+s^{2}=d^{2}$
5
6

Use this formula on an example square. These steps have proven that the formula Area = ${frac {d^{2}}{2}}$ works for all squares. Just plug in the length of the diagonal for d and solve.^[5]

1

Find the diagonal from the length of a side.^[6] The Pythagorean theorem for a square with side s and diagonal d gives you the formula $2s^{2}=d^{2}$ . Solve for d if you know the side lengths and want to find the length of the diagonal:
2
3

Add New Question

Question

A square has side lengths of 26.2 m, 21.4m, 27m, and 24.3m. How can I get the diagonal of square?

This shape is not a square, since it does not have equal sides. It is an irregular quadrilateral, either a trapezoid or an irregular shape with no name. Draw a right triangle inside the shape with the diagonal as the hypotenuse. If you have enough information to calculate the height and base of this right triangle (usually with trigonometry), you can use Pythagoras’ Theorem to find the diagonal. The two diagonals will be different lengths, since the shape is not symmetrical.
Question

What is the area of a school lawn with a width of 69 meters?

Assuming it is a square or rectangle, you have to know the other dimension, too.
Question

How did I find the length of side of each square?

LyKaxandra Caimoy

Community Answer

Suppose that the diagonal is 8. Square 8, so you will get 64. Now divide 64 by 2, you will get 32. Get the square root of 32. That is the length of the side of a square. The square root of 32 is equal to 4 square root of 2.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

If you don’t have a calculator and you need a more precise estimate for the square root of 2, there are ways to estimate it by hand. The Newton-Raphson method is one example.^[8]
This simple equation is used in many fields, including crystallography, chemistry, and art. For example, you can use it to calculate the area of landscape you can see when surveying, or when using perspective in photography or painting, by measuring the distance you’ve walked and imagining a grid with that distance as the diagonal.

About This Article

Article SummaryX

To find the area of a square using the length of its diagonal, use the formula area = d^2 divided by 2, where d is the length of the diagonal. Just square the length of the diagonal and then divide that number by 2 to find the square’s area. To learn how to find the length of a square’s sides using the diagonal, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,059,735 times.

Did this article help you?

Источник

Площадь квадрата через сторону или диагональ

Зная сторону

или диагональ квадрата, можно найти его площадь

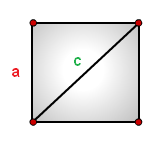
a – сторона квадрата

c – диагональ

Формула площади квадрата через сторону a, (S):

Калькулятор – вычислить, найти площадь квадрата:

Формула площади квадрата через диагональ c, (S):

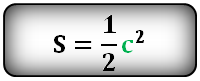
Подробности

Автор: Administrator

Опубликовано: 07 сентября 2011

Обновлено: 13 августа 2021

Источник

Советы

Об этой статье

Была ли эта статья полезной?

Площадь квадрата (по диагонали): онлайн-калькулятор

Вычисление площади квадрата по диагонали онлайн

Содержание:

Формула площади квадрата через сторону

Формула площади квадрата через диагональ

Формула площади квадрата через радиус вписанной окружности

Формула площади квадрата через радиус описанной окружности

Формула площади квадрата через периметр

Примеры задач на нахождение площади квадрата

Video

About This Article

Did this article help you?

Площадь квадрата через сторону или диагональ

Вам также может понравиться

Как найти стороны трапеции если известны биссектрисы

Как составить объявление на продажу дома в деревне

Как можно найти магнит в земле

Добавить комментарий Отменить ответ