Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
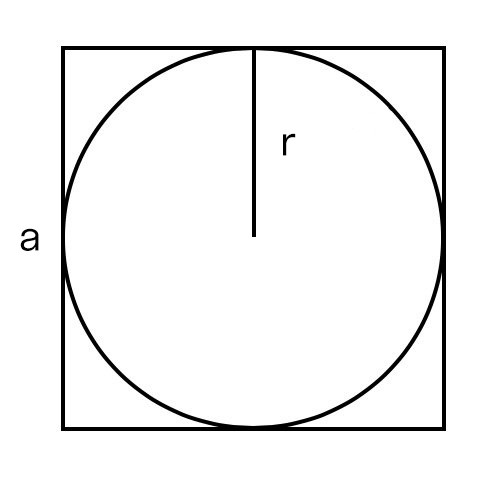
Cторона квадрата, диаметр вписанной окружности (L)
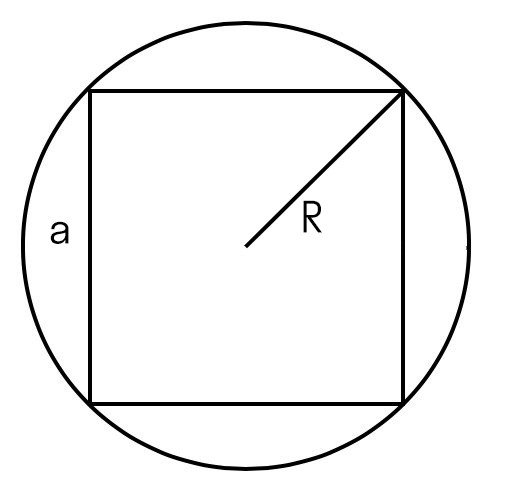
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Cторона, диаметр вписанной окружности (L) = 1
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*1^{2}}) = 1.41
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{1}{2}) = 0.5
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{1.41}{2}) = 0.71
Периметр (P) = (L*4) = (1*4) = 4
Площадь (S) = (L^{2}) = (1^{2}) = 1
Площадь квадрата равна квадрату длины стороны.
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a2, где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d2 : 2, где d — диагональ.
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r2, где r — это радиус вписанной окружности.
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R2, где R — это радиус описанной окружности.
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Важно!
Задачку не решить, если длина и ширина даны в разных единицах. Для правильного решения переведите все данные к одной единице измерения, и все получится.
Популярные единицы измерения площади:
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Как решаем:
-
Воспользуемся формулой: S = d2 : 2.
-
Подставим в формулу значение диагонали: S = 902 : 2 = 4050 мм2.
Ответ: 4050 мм2.
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Как решаем:
-
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d -
Диаметр окружности равен двум радиусам:
d = 2r -
Получается, что сторона равна двум радиусам:
a = 2r -
Используем формулу нахождения площади квадрата через сторону:
S = a2 -
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r)2
S = 4r2 -
Теперь подставим значение радиуса в формулу площади:
S = 4 × 242 = 2304 см2
Ответ: 2304 см2.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Cторона, диаметр вписанной окружности (L) = 1
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*1^{2}}) = 1.41
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{1}{2}) = 0.5
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{1.41}{2}) = 0.71
Периметр (P) = (L*4) = (1*4) = 4
Площадь (S) = (L^{2}) = (1^{2}) = 1
- Главная
- Справочник
- Как найти площадь квадрата
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь квадрата
Поможем сделать домашку Online
Первое занятие бесплатно
Перейти
Решение задачи по геометрии
Выполнение 1-3 дня
от 150 ₽
Заказать
Подробнее
Контрольные по геометрии
Выполнение 1–4 дня
от 310 ₽
Заказать
Подробнее
Контрольные по математике
Выполнение 1–4 дня
от 260 ₽
Заказать
Подробнее
Содержание:
- Формула
- Примеры вычисления площади квадрата
Формула
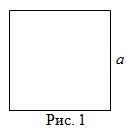
Чтобы найти площадь квадрата (рис. 1), надо длину его стороны возвести в квадрат, то есть
$$S=a^2$$
Напомним, что квадратом называется правильный четырехугольник, у которого все стороны и все углы равны.
Примеры вычисления площади квадрата
Пример
Задание. Найти площадь квадрата со стороной 3 см.
Решение. Площадь квадрата равна квадрату его стороны, то есть
$S=3^2=9$(см2)
Ответ. $S=3^2=9$ (см2)
Все формулы площади
Калькулятор площади квадрата

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Узнать стоимость
Пример
Задание. Найти площадь квадрата, диагональ которого равна 2 м.
Решение. Известно, что сторона
$a$ квадрата связана с его диагональю $d$ соотношением:
$$d=a sqrt{2}$$
тогда отсюда находим, что
$a=frac{d}{sqrt{2}}=frac{2}{sqrt{2}}=sqrt{2}$(м)
А тогда искомая площадь
$S=(sqrt{2})^{2}=2$ (м2)
Ответ. $S=2$ (м2)
Читать дальше: как найти площадь прямоугольника.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Поможем выполнить
любую работу
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Контрольные, курсовые, дипломные
Узнать подробнее
Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Краткая теория
- Формулы
- Теоремы
- Свойства
- Таблицы
Теоретический материал
- Формулы и свойства логарифмов
- Таблица интегралов
- Тригонометрические формулы
- Таблица степеней
- Формулы и свойства степеней
- Формулы площади
- Таблица Лапласа
- Формулы объема
Все еще сложно?
Наши эксперты помогут разобраться
Все услуги
Дипломные работы
Выполнение 2-3 недели
от 7000 ₽
Курсовые работы
Выполнение 5-7 дней
от 1500 ₽
Контрольные работы
Выполнение 1–4 дня
от 260 ₽
Написание рефератов
Выполнение 2-5 дней
от 650 ₽
Решение задач
Выполнение 1–3 дня
от 90 ₽
Написание диссертаций
Выполнение 2-3 месяца
от 19 000 ₽
Как найти площадь треугольника
Как найти площадь эллипса
Как найти площадь
Как найти площадь ромба
Не получается написать работу самому?
Доверь это кандидату наук!
Я даю согласие на обработку своих персональных данных в соответствии с Политикой
конфиденциальности и принимаю условия Договора публичной оферты
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
Прикрепить файл
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные