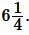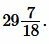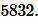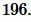Как найти площадь квадрата в квадратных миллиметрах

Онлайн калькулятор выразит площадь в квадратных миллиметрах. Введите любые из единиц измерения площади (целые или дробные) – Квадратные километры км², кв.км, km²; Гектары га, ha; Сотки ар, а; Квадратные метры м², кв.м, m²; Квадратные дециметры дм², кв.дм, dm²; Квадратные сантиметры см², кв.см, cm²; Квадратные миллиметры мм², кв.мм, mm². Нажав кнопку «вычислить» калькулятор выполнит расчёт, результат будет выражен в квадратных миллиметрах.

Например: вырази в квадратных миллиметрах 7 см² = 700 кв. мм.

Онлайн калькулятор. Площадь квадрата

Используя этот онлайн калькулятор, вы сможете найти площадь квадрата.

Воспользовавшись онлайн калькулятором для вычисления площади квадрата, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

Найти площадь квадрата

Выберите известную величину:

a =   

Площадь в   

Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.

Площадь квадрата онлайн

С помощю этого онлайн калькулятора можно найти площадь квадрата. Для нахождения площади квадрата, введите известные данные в ячейку и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Площадь квадрата. Определение

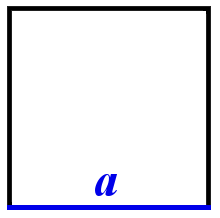
Определение 1. Площадь квадрата − это величина той части плоскости, которую занимает квадрат.

Единицы измерения площади квадрата

За единицу измерения площадей применяют квадрат, сторона которого равна единице измерения отрезков. В качестве единицы измерения площадей принимают квадраты со сторонами 1мм, 1см, 1дм, 1м и т.д (Рис.1). Такие квадраты назыают квадратным миллиметром, квадратным сантиметром, квадратным дециметром, квадратным метром и т.д., соответственно. Обозначаются они мм², см², дм², м² и т.д., соответственно.

Если выбрана единица измерения, то площадь измеряемого объекта (квадрата, треугольника, прямоугольника, многоугольника и т.д.)определяется положительным числом, которая определяет сколько раз единица измерения и ее части укладываются в данном объекте.

Для измерения отдельных плоских фигур используются специальные формулы. В данной статье мы выведем формулу для вычисления площади квадрата.

Площадь квадрата. Доказательство

Теорема 1. Площадь S квадрата со стороной a равна .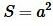

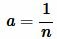
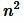
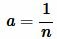
Доказательство. Пусть n целое неотрицательное число и пусть . Рассмотрим квадрат со стороной 1 (Рис.2). Разделим этот квадрат по ветрикали и по горизонлали на n равных частей. Получим маленьких квадратов состоронами . Поскольку 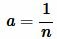площадь большого квадрата равна 1 (так как является единицей измерения), то очевидно, что площадь маленького квадрата равна:

а поскольку , то имеем:

Пусть теперь a является конечной десятичной дробью, содержащую n знаков после запятой. (Если n=0, то a будет целым числом). Тогда a можно представить в виде обыкновенной дроби, умножив и делив на :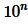

откуда

где m − целое число.

Возьмем квадрат со стороной a и разделим его по горизонлали и вертикали на m ровных частей. Получим m² маленьких квадратов (Рис.3).

Тогда, учитывая (2), сторона каждого квадрата равна:

По формуле (1) площадь маленького квадрата равна:

Следовательно, площадь квадрата со стороной a равна:

Пусть, далее, число a представляет собой бесконечную десятичную дробь. Рассмотрим число a_n которая получается из a отбрасыванием всех десятичных знаков после запятой, начиная с (n+1)-го. Поскольку a отличается от a_n не более, чем на 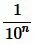, то имеем:

откуда

Из неравенства (4) следует, что площадь S квадрата со стороной a заключена между площадью квадрата со стороной a_n и площадью квадрата со стороной 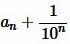(Рис.4), т.е.

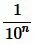
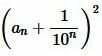
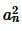
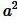
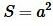
При неограниченном увеличении числа n, число будет становиться сколь угодно малым и, следовательно, число будет сколь угодно мало отличаться от . Тогда из неравенства (5) следует, что число S будет мало отличаться от числа . Следовательно они равны, т.е. .

Площадь квадрата по стороне

Из вышеизложенного доказательства получили, что площадь квадрата равна:

где ( small a ) сторона квадрата.

Пример 1. Сторона квадрата равна 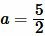. Найти площадь квадрата.

Решение. Для нахождения плошади квадрата воспользуемся формулой (6). Подставляя 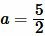в (6), получим:

Ответ:

Площадь квадрата по диагонали

Пусть известна диагональ ( small d ) квадрата (Рис.5). Найдем площадь квадрата.

Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Для этого воспользуемся теоремой Пифагора:

Подставляя (7) в (6), получим:

то есть площадь квадрата по диагонали вычисляется из следующей формулы:

Пример 2. Диагональ квадрата равна 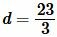. Найти площадь квадрата.

Решение. Для нахождения плошади квадрата воспользуемся формулой (8). Подставляя 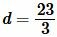в (8), получим:

Ответ:

Площадь квадрата по радиусу вписанной окружности

Пусть известен ( small r ) радиус окружности вписанной в квадрат (Рис.6). Найдем площадь квадрата.

Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Нетрудно заметить, что радиус ( small r ) равна половине стороны ( small a ) квадрата, т.е.

Подставляя (9) в (6), получим:

или

Пример 3. Радиус вписанной в квадрат окружности равен 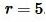. Найти площадь квадрата.

Решение. Для нахождения плошади квадрата воспользуемся формулой (10). Подставляя 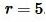в (10), получим:

Ответ:

Площадь квадрата по радиусу описанной окружности

Пусть известен ( small R ) радиус окружности описанной около квадрата (Рис.7). Найдем площадь квадрата.

Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Восрользуемся теоремой Пифагора:

Подставляя (11) в (6), получим:

Пример 4. Радиус описанной окружности равен 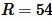. Найти площадь квадрата.

Решение. Для нахождения площади квадрата воспользуемся формулой (12). Подставляя 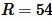в (12), получим:

Ответ:

Площадь квадрата по периметру

Пусть известен периметр ( small P ) квадрата. Найдем площадь квадрата. По периметру можно найти сторону квадрата:

Подставляя (13) в (6), получим:

то есть площадь квадрата через периметр равна:

Пример 5. Периметр квадрата равен 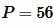. Найти площадь квадрата.

Решение. Для нахождения площади квадрата воспользуемся формулой (14). Подставляя 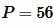в (14), получим:

Ответ:

Смотрите также:

• Квадрат. Онлайн калькулятор

Калькулятор для расчета площади

Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:

Прямоугольник; Параллелограмм; Круг; Сектор круга;

Треугольник; Правильный многоугольник; Эллипс; Трапеция.

Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.

Способ нахождения площади треугольника:

a=
b=
c=

Вычислить

Рассчитать площадь круга, если известен:

r=

Вычислить

Способ нахождения площади параллелограмма:

a=
h=

Вычислить

Рассчитать площадь сектора круга, если известен:

r=
θ=

Вычислить

Способ нахождения площади трапеции:

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.

Метрические единицы измерения площади:
Квадратный метр, производная единица системы СИ 1 м2 =	1 са (сантиар)
Квадратный километр – 1 км2 =	1 000 000 м2
Гектар – 1 га =	10 000 м2
Ар (сотка) – 1 а =	100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м)
Квадратный дециметр, 100 дм2 =	1 м2;
Квадратный сантиметр, 10 000 см2 =	1 м2;
Квадратный миллиметр, 1 000 000 мм2 =	1 м2.

Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.