Как найти площадь квадрата в метрах квадратных

Как найти площадь квадрата в метрах квадратных

Как рассчитать площадь квадрата

На данной странице калькулятор поможет рассчитать площадь квадрата онлайн. Для расчета задайте длину стороны или диагональ.

Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба.

Через сторону

Площадь квадрата через сторону

Формула для нахождения площади квадрата через сторону:

a – сторона квадрата.

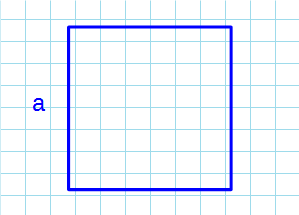
Через диагональ

Площадь квадрата через диагональ

Формула для нахождения площади квадрата через диагональ:

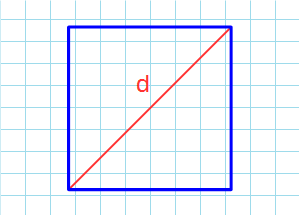
d – диагональ квадрата.

Источник
  1. Площадь квадрата по стороне
  2. Площадь квадрата по диагонали
  3. Площадь квадрата по периметру
  4. Площадь квадрата по радиусу описанной окружности
  5. Площадь квадрата по радиусу вписанной окружности
  6. Площадь квадрата вписанного в окружность, по известной длине окружности
  7. Площадь квадрата вписанного в окружность, по известной площади окружности
  8. Площадь квадрата через длину окружности, вписанной в этот квадрат
  9. Площадь квадрата через площадь окружности, вписанной в этот квадрат

Площадь квадрата по стороне

Площадь квадрата по стороне

Формула площади квадрата по стороне

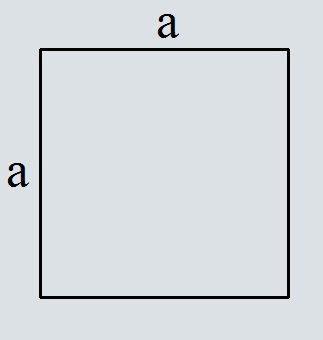
Где S – площадь квадрата,
a – сторона квадрата

Площадь квадрата по диагонали

Площадь квадрата по диагонали

Формула площади квадрата по диагонали

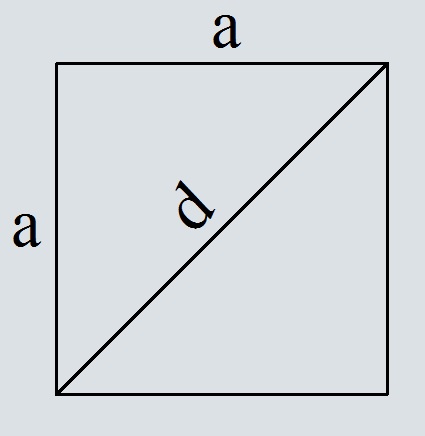
Где S – площадь квадрата,
d – диагональ квадрата

Площадь квадрата по периметру

Площадь квадрата по периметру

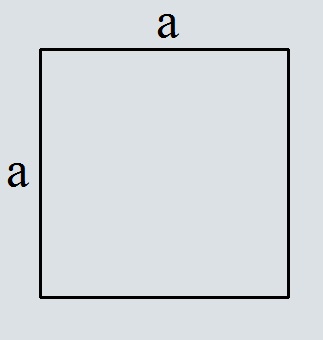
Формула площади квадрата по периметру

Где S – площадь квадрата,
P – периметр квадрата

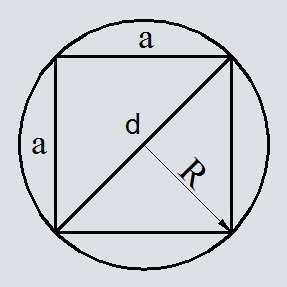
Площадь квадрата по радиусу описанной окружности

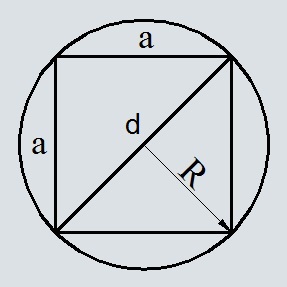
Площадь квадрата по радиусу описанной окружности

Формула площади квадрата по радиусу описанной окружности

Где S – площадь квадрата,
R – радиус описанной окружности

Площадь квадрата по радиусу вписанной окружности

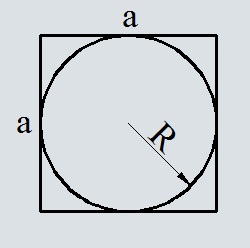
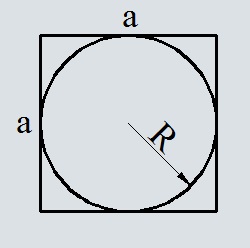
Площадь квадрата по радиусу вписанной окружности

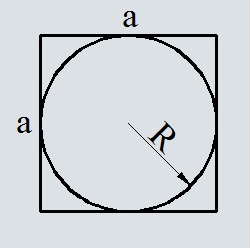
Формула площади квадрата по радиусу вписанной окружности

Где S – площадь квадрата,
R – радиус вписанной окружности

Площадь квадрата вписанного в окружность по известной длине этой окружности

Введите длину окружности l

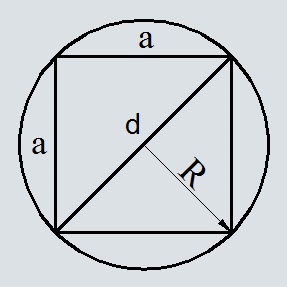
Площадь квадрата вписанного в окружность по известной длине этой окружности

Формула площади квадрата вписанного в окружность по известной длине этой окружности

Где S – площадь квадрата,
l – длина окружности

Площадь квадрата вписанного в окружность по известной площади этой окружности

Введите площадь окружности Sокр

Площадь квадрата вписанного в окружность по известной площади этой окружности

Формула площади квадрата вписанного в окружность по известной площади этой окружности

Где S – площадь квадрата,
Sокр – площадь окружности

Площадь квадрата через длину окружности вписанной в этот квадрат

Введите длину окружности l

Площадь квадрата через длину окружности вписанной в этот квадрат

Формула площади квадрата через длину окружности вписанной в этот квадрат

Где S – площадь квадрата,
l – длина окружности

Площадь квадрата через площадь окружности вписанной в этот квадрат

Введите площадь окружности Sокр

Площадь квадрата через площадь окружности вписанной в этот квадрат

Формула площади квадрата через площадь окружности вписанной в этот квадрат

Где S – площадь квадрата,
Sокр – площадь окружности

Источник

Площадь квадрата через сторону

{S = a ^2}

На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.

Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.

Содержание:
  1. калькулятор площади квадрата
  2. формула площади квадрата через сторону
  3. формула площади квадрата через диагональ
  4. формула площади квадрата через радиус вписанной окружности
  5. формула площади квадрата через радиус описанной окружности
  6. формула площади квадрата через периметр
  7. примеры задач

Формула площади квадрата через сторону

Площадь квадрата через сторону

S = a ^2

a – сторона квадрата

Формула площади квадрата через диагональ

Площадь квадрата через диагональ

S=dfrac{d^2}{2}

d – диагональ квадрата

Формула площади квадрата через радиус вписанной окружности

Площадь квадрата через радиус вписанной окружности

S = 4r^2

r – радиус вписанной окружности

Формула площади квадрата через радиус описанной окружности

Площадь квадрата через радиус описанной окружности

S = 2R^2

R – радиус описанной окружности

Формула площади квадрата через периметр

Площадь квадрата через периметр

S = dfrac{P^2}{16}

P – периметр квадрата

Примеры задач на нахождение площади квадрата

Задача 1

Найдите площадь квадрата если его диагональ равна 1.

Решение

Для решения задачи воспользуемся формулой.

S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2

Ответ: 0.5 см²

Проверим ответ на калькуляторе .

Задача 2

Найдите площадь квадрата, описанного вокруг окружности радиуса 83.

Решение

Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.

S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2

Ответ: 13778 см²

Проверим ответ с помощью калькулятора .

Задача 3

Найдите площадь квадрата если его сторона равна 8 см.

Решение

Используем первую формулу.

S = a ^2 = 8 ^2 = 64 : см^2

Ответ: 64 см²

Проверим результат на калькуляторе .

Задача 4

Найдите площадь квадрата периметр которого равен 456 см.

Решение

Используем формулу для площади квадрата через периметр.

S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2

Ответ: 12996 см²

Проверка .

Задача 5

Найдите площадь квадрата со стороной 15 см.

Решение

Воспользуемся формулой площади квадрата через сторону.

S = a ^2 = 15 ^2 = 225 : см^2

Ответ: 225 см²

Проверка .

Источник

Площадь квадрата, как посчитать площадь квадрата. Формула площади квадрата.

  • Формула площади квадрата.

    Площадь квадрата обозначается буквой – S.

    Сторона квадрата обозначается любой буквой, которая вам нравится, кроме занятой S.

    Обычно сторону обозначают буквой – “a”

    Формула площади квадрата : площадь квадрата равна стороне квадрата во второй степени.

    Либо может встречаться вот такая формулировка площади квадрата:

    Площадь квадрата равна произведению стороны квадрата на себя.

    Формула площади квадрата.

    S = a²

    Где S – площадь квадрата,

    a – длина одной из сторон.

  • Пример подсчета площади квадрата

    Как вычислить площадь квадрата?

    Для того, чтобы найти площадь квадрата – нужно знать длину стороны квадрата.

    Предположим, что у нас есть квадрат, площадь которого нам требуется узнать!

    Пусть это будет 10см.

    Условие задачи :

    Сколько будет площадь квадрата со стороной 10см.

    Решение задачи – найти площадь квадрата:

    Как вы помните из правила высчитывания площади квадрата – нужно сторону квадрата умножить на себя или возвести во вторую степень.

    S = a²

    Умножаем сторону квадрата 10, на себя, на 10 :

    10 * 10 = 100см2
    Ответ :
    Площадь квадрата со стороной 10см, будет равна 100см2
    100см2

  • Как найти площадь квадрата если известен периметр!?

    Условие задачи : найдите площадь квадрата, если известен периметр = 32см.

    Решение задачи – найти площадь квадрата:

    Для того, чтобы узнать площадь квадрата по его периметру нам понадобится формула подсчета периметра квадрата:

    P = 4a

    Решение задачи - найти площадь квадрата:

    Далее нам нужно 32 разделить на 4, мы найдем длину одной стороны квадрата.

    И далее по формуле площади квадрата узнаем его площадь :

    S = a² = 4² = 16см²

    Ответ задачи :

    Квадрат, у которого периметр 32 см, площадь равна 16см²

  • Как найти площадь квадрата если известна диагональ!?

    Условие задачи : найдите площадь квадрата, если известна диагональ квадрата = 8см.

    Решение задачи – найти площадь квадрата:

    Для того, чтобы найти диагональ квадрата, нам нужно вспомнить формулу пифагора :

    a² + a² = d²

    Решение задачи - найти площадь квадрата:

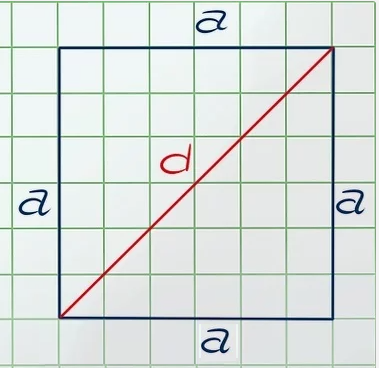
    Немного нужно преобразовать :

    a² + a² = d² -> 2a² = d² -> a² = d²/2

    А если S = a², то S = d²/2

    И далее нам нужно подставить нашу диагональ :

    S = 8²/2 = 64/2 = 32см².

    Ответ :

    Если диагональ квадрата равна – 8см, То площадь квадрата равна – 32см².

  • Какая единица измерения площади квадрата!?

    После того, как я написал страницу и началась выдача страницы, интересный поисковый вопрос : “площадь квадрата почему см2“.

    Человек, видимо, хотел спросить, откуда двойка в единице измерения площади квадрата!?

    Мы можем рассказать… о том, в какой единице измерения измеряются площадь квадрата и откуда там берется двойка!?

    Единица измерения площади квадрата

    Единица измерения площади квадрата – может быть, любая мера длины в квадрате.

    Если мера длины сантиметр, то площадь будет сантиметр в квадрате – см².

    Если мера длины метр, то площадь будет метр в квадрате – м².

    Если мера длины километр, то площадь будет километр в квадрате – км². и т.д…

    Почему единица измерения площади квадрата пишется с двойкой

    Обычно в младших классах, на единицу измерения не обращают внимания. Но уже в старших классах на это обращают некоторое внимание!

    Почему единица площади(и в том числе квадрата) обозначают двойкой чуть выше буквеного выражения!?

    Если мы вспомним, что площадь квадрата равна умноженной длины стороны на себя и напишем единицу измерения… то мы увидим откуда берется двойка…

    Давайте покажем на примере…

    Пусть надо найти площадь квадрата со стороной 12 см.

    Так и записываем в формулу :

    S = 12см * 12см

    Далее никуда единицу измерения не убираем, а умножаем их между собой, вот отсюда и получается квадратные сантиметры(или другая мера длины в квадрате) :

    12*12(см*см) = 12²см² = 144см²

  • Как найти площадь квадрата зная радиус вписанной окружности!?

    Задача :

    Как найти площадь квадрата зная радиус вписанной окружности!?

    Это очень простая задача!

    Диаметр вписанной окружности равна стороне квадрата.

    Диаметр окружности равен 2R.

    Значит сторона квадрата равна 2R.

    Далее вспоминаем формулу площади квадрата – S = a², где a – сторона квадрата, которая равна = 2R.

    Значит площадь квадрата равна S = (2R)²

    Как найти площадь квадрата зная радиус вписанной окружности!?

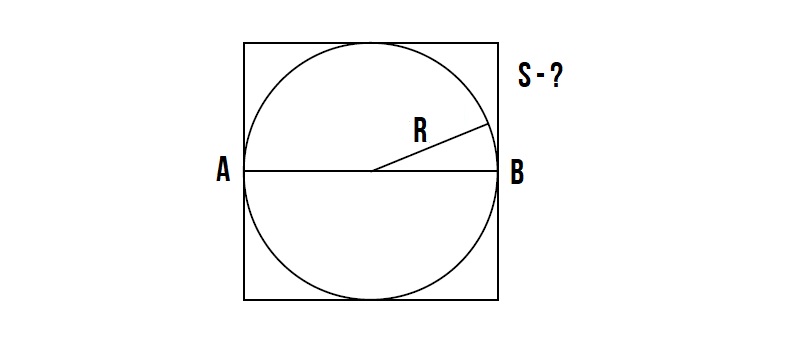
  • Как найти площадь квадрата зная радиус описанной окружности!?

    Задача :

    Как найти площадь квадрата зная радиус описанной окружности!?

    Данная задача такая же простая, как и выше описанная!

    У нас известен радиус окружности описанной вокруг квадрата.

    Диаметр окружности AB равен диагонали квадрата AB и мы знаем, что диаметр окружности равен двум радиусам d = 2R.

    По диагонали квадрата мы уже один раз высчитывали площадь здесь -> S = d²/2

    Далее подставляем S = (2R)²/2

    Как найти площадь квадрата зная радиус описанной окружности!?

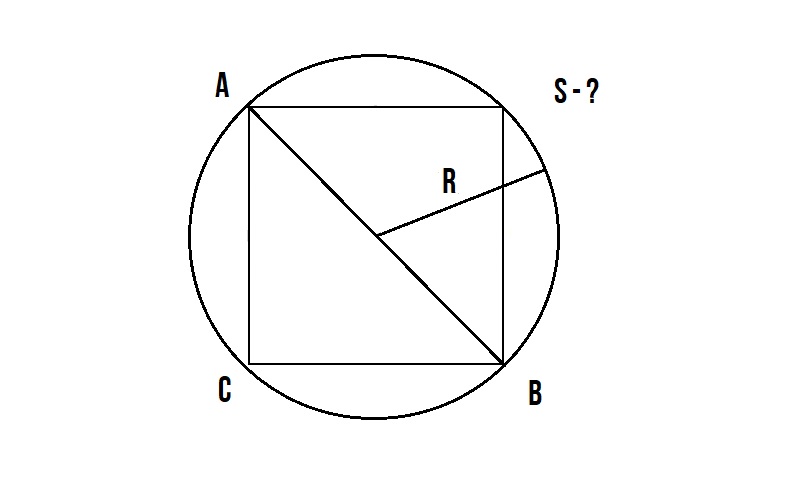
  • Найти площадь квадрата онлайн

    Для того чтобы посчитать площадь квадрата онлайн, вам требуется в поле :

    Сторона квадрата – заполнить значением стороны квадрата.

    И нажать кнопку посчитать.

    Источник

    Рассмотрим фигуру ниже:

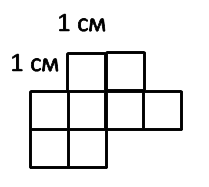
    определение площади

    Вся фигура состоит из 8 квадратов со стороной 1 см каждый.

    Площадь одного такого квадрата называют квадратным сантиметром и записывают:
    1 см2.

    Площадь всей фигуры 8 см2.

    Запомните!
    !

    Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.

    В математике для нахождения площади геометрических фигур используют специальные формулы,
    в которых площадь обозначается заглавной латинской буквой «S».

    Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.

    Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата,
    равна 1 м, то его площадь равна 1
    квадратному метру (1 м2); если длина
    его стороны равна 1 см, то его площадь
    равна 1 квадратному сантиметру
    (1 см2).

    Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.

    Как перевести квадратные единицы

    Рассмотрим квадрат со стороной 1 см.

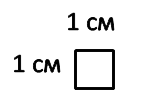
    квадратный сантиметр

    Его площадь равна:

    S = 1 см · 1 см = 1см2

    Рассмотрим квадрат со стороной 1 м.

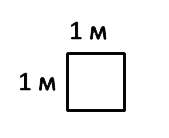
    квадратный метр

    Его площадь равна:

    S = 1 м · 1 м = 1 м2

    Известно, что: 1 м = 100 см

    1 м2 = 1 м · 1 м = 100 см · 100 см = 10 000 см2

    Увеличим сторону квадрата равную 1 м в
    10 раз. Получим квадрат со
    стороной 10 м.

    ap

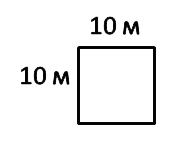
    Площадь такого квадрата называют ар или сотка.

    S = 10 м · 10 м = 100 м2

    В одном аре — сто квадратных метров.

    Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».

    1 ар (сотка) = 100 м2

    Чтобы выразить ар в cм2, вспомним, что 1 м2 = 10 000 см2.

    Значит: 1 ар (сотка) = 100 м2 = 100 · 10 000 см2 = 1 000 000 см2

    Увеличим сторону квадрата равную 10 м в 10 раз.
    Получим квадрат со
    стороной 100 м.

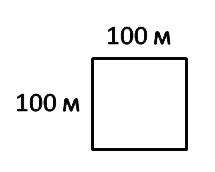
    гектар

    Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование
    проговаривается полностью.

    Выразим гектар в квадратных метрах.

    1 га = 100 м · 100 м = 10 000 м2

    Теперь определим, сколько в одном гектаре аров.

    1 ар = 100 м2

    Значит: 10 000 м2 : 100 м2 = 100 (ар)

    1 га = 100 ар

    Для измерения больших площадей, например, территорий государств, материков используют квадратный километр.
    То есть квадрат со стороной 1 км и
    площадью 1 км2.

    1 км = 1000 м

    1 км2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м2

    Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.

    Таблица переводов квадратных единиц

    Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.

    га ар м2 cм2
    1 км2 100 га 10 000 ар 1 000 000 м2 1 000 000 000 cм2
    1 га 1 га 100 ар 10 000 м2 100 000 000 cм2
    1 ар 0,01 га 1 ар 100 м2 1 000 000cм2
    1 м2 0,000 1 га 0,01 ар 1 м2 10 000 cм2

    Ваши комментарии

    Важно!
    Галка

    Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

    «ВКонтакте».

    Пришелец пожимает плечами

    Оставить комментарий:

    12 сентября 2018 в 20:57

    Дмитрий Мозговой
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 1

    (^-^)
    Дмитрий Мозговой
    Профиль
    Благодарили: 0

    Сообщений: 1

    Внутри большего квадрата расположен меньший квадрат площади 73. Известно, что длины отрезков, на которые сторона большего квадрата делится вершинами меньшего квадрата, — натуральные числа. Чему равна площадь большего квадрата?

    0
    Спасибоthanks
    Ответить

    14 октября 2018 в 20:45
    Ответ для Дмитрий Мозговой

    Дарья Тихая
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 1

    (^-^)
    Дарья Тихая
    Профиль
    Благодарили: 0

    Сообщений: 1


    146

    0
    Спасибоthanks
    Ответить

    21 октября 2018 в 15:44
    Ответ для Дмитрий Мозговой

    Владимир Шварцман
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 1

    (^-^)
    Владимир Шварцман
    Профиль
    Благодарили: 0

    Сообщений: 1


    Пусть отрезки большего квадрата  a и  в. Тогда  а2 + в2  =73 Сумма двух чисел нечётна если одно чёт., а второе нечёт. Это 1,9,25,49 и 4, 16,36.64 Легко видеть, что это числа 9 и 64.Т.е. а=3 и в=8 Пл. большого квадрата=112 =121 

    0
    Спасибоthanks
    Ответить

    12 ноября 2018 в 3:31
    Ответ для Дмитрий Мозговой

    Евгений Фёдоров
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 60

    (^-^)
    Евгений Фёдоров
    Профиль
    Благодарили: 0

    Сообщений: 60


    Неверно.

    0
    Спасибоthanks
    Ответить

    22 июня 2016 в 20:17

    Клара Чукаева
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 1

    (^-^)
    Клара Чукаева
    Профиль
    Благодарили: 0

    Сообщений: 1

    д вечер. у меня вопрос: как найти площадь таблички размером 50 см на 75 см? если перемножить, как нам предлагает школьная программа, то получается 3750 см2, разве это возможно? я ошибаюсь? напишите формулу для расчета пожалуйста?

    0
    Спасибоthanks
    Ответить

    24 июня 2016 в 12:18
    Ответ для Клара Чукаева

    Павел Асафов
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 2

    (^-^)
    Павел Асафов
    Профиль
    Благодарили: 0

    Сообщений: 2


    Здравствуйте! Все верно.
    Формула площади прямоугольника S=a · b
    (a)50 · (b)75=3750 см2
    Может вы спутали с периметром? Периметр будет равен 250 см
    a ·2+b · 2

    0
    Спасибоthanks
    Ответить

    16 января 2016 в 18:29

    Надюша Бисерова
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 1

    (^-^)
    Надюша Бисерова
    Профиль
    Благодарили: 0

    Сообщений: 1

    ширина прамоугольника 23 см. на сколько увеличиться площадь прамоугольника, если его длину увеличить на 3 см?
    подскажите решение пожалуйста

    0
    Спасибоthanks
    Ответить

    21 января 2016 в 16:17
    Ответ для Надюша Бисерова

    Сергей Фадеев
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 6

    (^-^)
    Сергей Фадеев
    Профиль
    Благодарили: 0

    Сообщений: 6



    на 3 см квадратных
    если я не ошибаюсь взависимости от длины

    0
    Спасибоthanks
    Ответить

    24 января 2016 в 13:50
    Ответ для Надюша Бисерова

    Инна Шабрашина
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 5

    (^-^)
    Инна Шабрашина
    Профиль
    Благодарили: 0

    Сообщений: 5


    увеличится на 69

    0
    Спасибоthanks
    Ответить

    12 октября 2015 в 17:22

    Мося Мося
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 1

    (^-^)
    Мося Мося
    Профиль
    Благодарили: 0

    Сообщений: 1

    найди площадь квадрата периметр которого 280см

    0
    Спасибоthanks
    Ответить

    1 июля 2016 в 14:20
    Ответ для Мося Мося

    Евгений Колосов
    (^-^)
    Профиль
    Благодарили: 12

    Сообщений: 197

    (^-^)
    Евгений Колосов
    Профиль
    Благодарили: 12

    Сообщений: 197


    Для нахождения площади квадрата в данном случае нам понадобятся две формулу, а именно:
    1) Формула периметра квадрата P=4a. Подробно про периметр читаем здесь http://math-prosto.ru/?page=pages/perimeter/perimeter.php 
    2) Формула площади квадрата S=a2. Подробно читать здесь http://math-prosto.ru/?page=pages/area/area_figures.php

    Приступим к решению. Выразим сторону квадрата из формулы периметра:
    P=4a
    a=P: 4
    a= 280: 4 = 70 (см)
    Теперь воспользуемся формулой площади квадрата: 
    S=a2
    S=702=4900 (см2)
    Ответ: площадь квадрата равна 4900 см2

    0
    Спасибоthanks
    Ответить

    4 сентября 2015 в 15:44

    Игорь Винников
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 2

    (^-^)
    Игорь Винников
    Профиль
    Благодарили: 0

    Сообщений: 2

       Площадь прямоугольника64мс2, одна из сторон 16см. Надо найти соседнюю сторону

    0
    Спасибоthanks
    Ответить

    1 сентября 2016 в 10:18
    Ответ для Игорь Винников

    Евгений Колосов
    (^-^)
    Профиль
    Благодарили: 12

    Сообщений: 197

    (^-^)
    Евгений Колосов
    Профиль
    Благодарили: 12

    Сообщений: 197


    Площадь прямоугольника рассчитывается по формуле S=a · b. Подставим значения в формулу и вычислим вторую сторону:
    64=16 · b
    b=64/16=4
    вторая сторона равна 4.
    проверка: 16 · 4 = 64.

    Ответ: Соседняя сторона прямоугольника равна 4 см.

    0
    Спасибоthanks
    Ответить

    6 июля 2015 в 17:48

    Дмитрий Рыжков
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 2

    (^-^)
    Дмитрий Рыжков
    Профиль
    Благодарили: 0

    Сообщений: 2

    Посмотрите, у вас не первый раз перепутаны буквы в примерах.Например посмотрите нм тему: площадь сложных фигур.там же треугольник обозначен одними буквами, а написано в примере другими совершенно. Никто не ответил по предыдущей теме.спасибо.

    0
    Спасибоthanks
    Ответить

    12 июля 2015 в 13:31
    Ответ для Дмитрий Рыжков

    Борис Гуров
    (^-^)
    Профиль
    Благодарили: 1

    Сообщений: 28

    (^-^)
    Борис Гуров
    Профиль
    Благодарили: 1

    Сообщений: 28


    Здравствуйте, Дмитрий.

    Благодарим Вас за указанное замечание. 

    Пожалуйста, укажите, более конкретно место ошибки.

    В уроке «Площадь сложных фигур» мы не нашли ошибку, о которой Вы написали.

    0
    Спасибоthanks
    Ответить

    17 мая 2015 в 10:59

    Соня Кизилова
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 1

    (^-^)
    Соня Кизилова
    Профиль
    Благодарили: 0

    Сообщений: 1

    Самостоятельная работа.
    Задание 3.
    На сколько частей разбивают плоскость 4 прямые, пересекающиеся в одное точке?
    Задание 2.
    Начертите угол MON. Отметьте точку K, лежащую внутри этого угла, и точку L, лежащую на отрезке NK.
    Задание 4.
    Постройте треугольник ABC со стороной AB= 6см,?ABC= 45градусов, ?BAC= 75 градусов.Помогите пожалуйстаcry… 

    0
    Спасибоthanks
    Ответить

    17 мая 2015 в 12:57
    Ответ для Соня Кизилова

    Ярослава Фесенко
    (^-^)
    Профиль
    Благодарили: 0

    Сообщений: 3

    (^-^)
    Ярослава Фесенко
    Профиль
    Благодарили: 0

    Сообщений: 3


    1.8 частей

    0
    Спасибоthanks
    Ответить

    Источник

    Добавить комментарий