Как найти площадь квадрата зная диаметр

Как найти площадь квадрата зная диаметр

Площадь квадрата через сторону

{S = a ^2}

На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.

Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.

Содержание:
  1. калькулятор площади квадрата
  2. формула площади квадрата через сторону
  3. формула площади квадрата через диагональ
  4. формула площади квадрата через радиус вписанной окружности
  5. формула площади квадрата через радиус описанной окружности
  6. формула площади квадрата через периметр
  7. примеры задач

Формула площади квадрата через сторону

Площадь квадрата через сторону

S = a ^2

a – сторона квадрата

Формула площади квадрата через диагональ

Площадь квадрата через диагональ

S=dfrac{d^2}{2}

d – диагональ квадрата

Формула площади квадрата через радиус вписанной окружности

Площадь квадрата через радиус вписанной окружности

S = 4r^2

r – радиус вписанной окружности

Формула площади квадрата через радиус описанной окружности

Площадь квадрата через радиус описанной окружности

S = 2R^2

R – радиус описанной окружности

Формула площади квадрата через периметр

Площадь квадрата через периметр

S = dfrac{P^2}{16}

P – периметр квадрата

Примеры задач на нахождение площади квадрата

Задача 1

Найдите площадь квадрата если его диагональ равна 1.

Решение

Для решения задачи воспользуемся формулой.

S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2

Ответ: 0.5 см²

Проверим ответ на калькуляторе .

Задача 2

Найдите площадь квадрата, описанного вокруг окружности радиуса 83.

Решение

Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.

S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2

Ответ: 13778 см²

Проверим ответ с помощью калькулятора .

Задача 3

Найдите площадь квадрата если его сторона равна 8 см.

Решение

Используем первую формулу.

S = a ^2 = 8 ^2 = 64 : см^2

Ответ: 64 см²

Проверим результат на калькуляторе .

Задача 4

Найдите площадь квадрата периметр которого равен 456 см.

Решение

Используем формулу для площади квадрата через периметр.

S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2

Ответ: 12996 см²

Проверка .

Задача 5

Найдите площадь квадрата со стороной 15 см.

Решение

Воспользуемся формулой площади квадрата через сторону.

S = a ^2 = 15 ^2 = 225 : см^2

Ответ: 225 см²

Проверка .

Источник

Как определить площадь квадрата

О чем эта статья:

3 класс, 8 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Формула нахождения площади квадрата

Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

S = a × a = a 2 , где S — площадь, a — сторона.

Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d 2 : 2, где d — диагональ.

Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

S = 4 × r 2 , где r — это радиус вписанной окружности.

Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

S = 2 × R 2 , где R — это радиус описанной окружности.

У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р 2 : 16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Популярные единицы измерения площади:

  • квадратный миллиметр (мм 2 );
  • квадратный сантиметр (см 2 );
  • квадратный дециметр (дм 2 );
  • квадратный метр (м 2 );
  • квадратный километр (км 2 );
  • гектар (га).

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Воспользуемся формулой: S = d 2 : 2.

Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .

Ответ: 4050 мм 2 .

Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.

Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d

Диаметр окружности равен двум радиусам:
d = 2r

Получается, что сторона равна двум радиусам:
a = 2r

Используем формулу нахождения площади квадрата через сторону:
S = a 2

Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2

Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2

Онлайн калькулятор площади вписанного в круг квадрата. Как узнать площадь вписанного в круг квадрата.

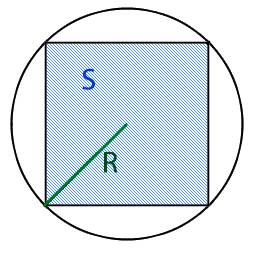
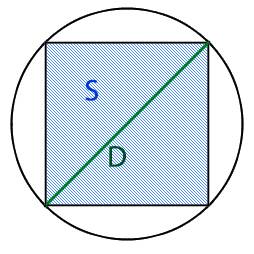
Вычислить площадь вписанного квадрата через:

Радиус круга R:

Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.

Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:

  1. либо площадь круга, обозначаемая буквой S,
  2. либо периметр круга, обозначаемый буквой P,
  3. либо радиус круга, обозначаемый буквой R,
  4. либо диаметр круга, обозначаемый буквой D.

Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой

Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,

мы можем узнать длину сторон квадрата используя теорему Пифагора

после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.

Формулы площадей всех основных фигур

1. Формула площади круга через радиус или диаметр

Зная диаметр или радиус круга, можно найти его площадь.

r – радиус круга

D – диаметр

Формула площади круга, (S):

2. Формула расчета площади треугольника

h – высота треугольника

a – основание

Площадь треугольника (S):

3. Площадь треугольника, формула Герона

a , b , c , – стороны треугольника

p– полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

4. Площадь прямоугольного треугольника по катетам

Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.

a , b – катеты треугольника

Формула площади прямоугольного треугольника, (S):

5. Как вычислить площадь равнобедренного треугольника ?

b – основание треугольника

a – равные стороны

h – высота

Формула площади треугольника через высоту h и основание b , ( S ):

Формула площади треугольника через, стороны a , b , (S):

6. Площадь равностороннего треугольника равна:

Формулы расчета, площади равностороннего треугольника.

a – сторона треугольника

h – высота

Площадь треугольника только через сторону a , (S):

Площадь треугольника только через высоту h , ( S ):

Площадь треугольника через сторону a и высоту h , (S):

7. Найти площадь треугольника, угол и две стороны

Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.

a , b , c – стороны треугольника

α , β , γ – углы

Формулы площади треугольника, через две стороны и угол между ними, ( S ):

8. Площадь треугольника по стороне и двум углам, формула.

a , b , c – стороны треугольника

α , β , γ – противолежащие углы

Площадь треугольника через сторону и два угла (S):

9. Формула расчета площади прямоугольника

b – длина прямоугольника

a – ширина

Формула площади прямоугольника, (S):

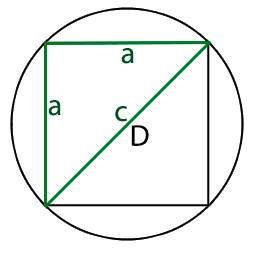
10. Как рассчитать площадь квадрата через диагональ или сторону

a – сторона квадрата

c – диагональ

Формула площади квадрата через сторону a , (S):

Формула площади квадрата через диагональ c , (S):

11. Формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма

α , β – углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма

H b – высота на сторону b

H a – высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ

d – меньшая диагональ

α , β – углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , (S):

12. Площадь произвольной трапеции

1. Формула площади трапеции через основания и высоту

b – верхнее основание

a – нижнее основание

m – средняя линия

h – высота трапеции

Формула площади трапеции, (S):

2. Формула площади трапеции через диагонали и угол между ними

d 1, d 2 – диагонали трапеции

α , β – углы между диагоналями

Формула площади трапеции, (S):

3. Формула площади трапеции через четыре стороны

b – верхнее основание

a – нижнее основание

c, d – боковые стороны

Формула площади трапеции, (S):

13. Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

b – верхнее основание

a – нижнее основание

c – равные боковые стороны

α – угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R – радиус вписанной окружности

D – диаметр вписанной окружности

O – центр вписанной окружности

H – высота трапеции

α , β – углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции

α , β – углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m – средняя линия трапеции

c – боковая сторона

α , β – углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b – верхнее основание

a – нижнее основание

h – высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

[spoiler title=”источники:”]

http://tamali.net/calculator/inscribed/square/area/

http://www-formula.ru/2011-09-19-02-39-24/2011-09-24-00-19-17

[/spoiler]

Источник

Площадь квадрата, как посчитать площадь квадрата. Формула площади квадрата.

  • Формула площади квадрата.

    Площадь квадрата обозначается буквой – S.

    Сторона квадрата обозначается любой буквой, которая вам нравится, кроме занятой S.

    Обычно сторону обозначают буквой – “a”

    Формула площади квадрата : площадь квадрата равна стороне квадрата во второй степени.

    Либо может встречаться вот такая формулировка площади квадрата:

    Площадь квадрата равна произведению стороны квадрата на себя.

    Формула площади квадрата.

    S = a²

    Где S – площадь квадрата,

    a – длина одной из сторон.

  • Пример подсчета площади квадрата

    Как вычислить площадь квадрата?

    Для того, чтобы найти площадь квадрата – нужно знать длину стороны квадрата.

    Предположим, что у нас есть квадрат, площадь которого нам требуется узнать!

    Пусть это будет 10см.

    Условие задачи :

    Сколько будет площадь квадрата со стороной 10см.

    Решение задачи – найти площадь квадрата:

    Как вы помните из правила высчитывания площади квадрата – нужно сторону квадрата умножить на себя или возвести во вторую степень.

    S = a²

    Умножаем сторону квадрата 10, на себя, на 10 :

    10 * 10 = 100см2
    Ответ :
    Площадь квадрата со стороной 10см, будет равна 100см2
    100см2

  • Как найти площадь квадрата если известен периметр!?

    Условие задачи : найдите площадь квадрата, если известен периметр = 32см.

    Решение задачи – найти площадь квадрата:

    Для того, чтобы узнать площадь квадрата по его периметру нам понадобится формула подсчета периметра квадрата:

    P = 4a

    Решение задачи - найти площадь квадрата:

    Далее нам нужно 32 разделить на 4, мы найдем длину одной стороны квадрата.

    И далее по формуле площади квадрата узнаем его площадь :

    S = a² = 4² = 16см²

    Ответ задачи :

    Квадрат, у которого периметр 32 см, площадь равна 16см²

  • Как найти площадь квадрата если известна диагональ!?

    Условие задачи : найдите площадь квадрата, если известна диагональ квадрата = 8см.

    Решение задачи – найти площадь квадрата:

    Для того, чтобы найти диагональ квадрата, нам нужно вспомнить формулу пифагора :

    a² + a² = d²

    Решение задачи - найти площадь квадрата:

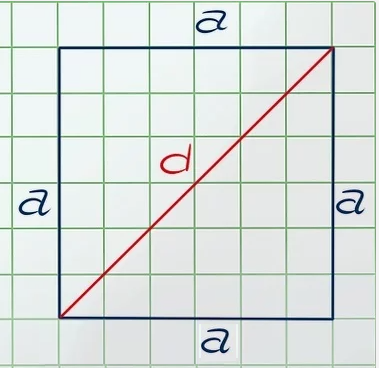
    Немного нужно преобразовать :

    a² + a² = d² -> 2a² = d² -> a² = d²/2

    А если S = a², то S = d²/2

    И далее нам нужно подставить нашу диагональ :

    S = 8²/2 = 64/2 = 32см².

    Ответ :

    Если диагональ квадрата равна – 8см, То площадь квадрата равна – 32см².

  • Какая единица измерения площади квадрата!?

    После того, как я написал страницу и началась выдача страницы, интересный поисковый вопрос : “площадь квадрата почему см2“.

    Человек, видимо, хотел спросить, откуда двойка в единице измерения площади квадрата!?

    Мы можем рассказать… о том, в какой единице измерения измеряются площадь квадрата и откуда там берется двойка!?

    Единица измерения площади квадрата

    Единица измерения площади квадрата – может быть, любая мера длины в квадрате.

    Если мера длины сантиметр, то площадь будет сантиметр в квадрате – см².

    Если мера длины метр, то площадь будет метр в квадрате – м².

    Если мера длины километр, то площадь будет километр в квадрате – км². и т.д…

    Почему единица измерения площади квадрата пишется с двойкой

    Обычно в младших классах, на единицу измерения не обращают внимания. Но уже в старших классах на это обращают некоторое внимание!

    Почему единица площади(и в том числе квадрата) обозначают двойкой чуть выше буквеного выражения!?

    Если мы вспомним, что площадь квадрата равна умноженной длины стороны на себя и напишем единицу измерения… то мы увидим откуда берется двойка…

    Давайте покажем на примере…

    Пусть надо найти площадь квадрата со стороной 12 см.

    Так и записываем в формулу :

    S = 12см * 12см

    Далее никуда единицу измерения не убираем, а умножаем их между собой, вот отсюда и получается квадратные сантиметры(или другая мера длины в квадрате) :

    12*12(см*см) = 12²см² = 144см²

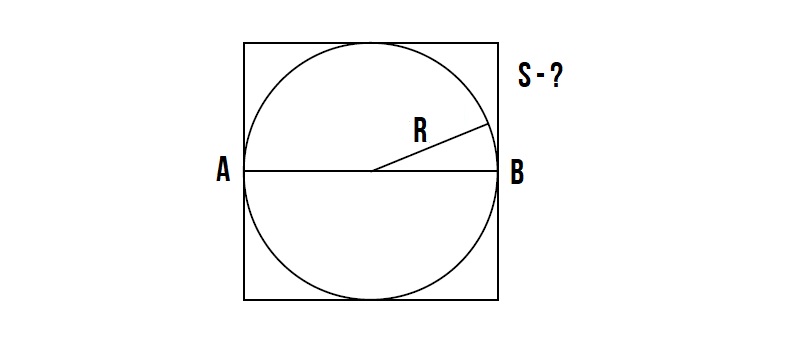
  • Как найти площадь квадрата зная радиус вписанной окружности!?

    Задача :

    Как найти площадь квадрата зная радиус вписанной окружности!?

    Это очень простая задача!

    Диаметр вписанной окружности равна стороне квадрата.

    Диаметр окружности равен 2R.

    Значит сторона квадрата равна 2R.

    Далее вспоминаем формулу площади квадрата – S = a², где a – сторона квадрата, которая равна = 2R.

    Значит площадь квадрата равна S = (2R)²

    Как найти площадь квадрата зная радиус вписанной окружности!?

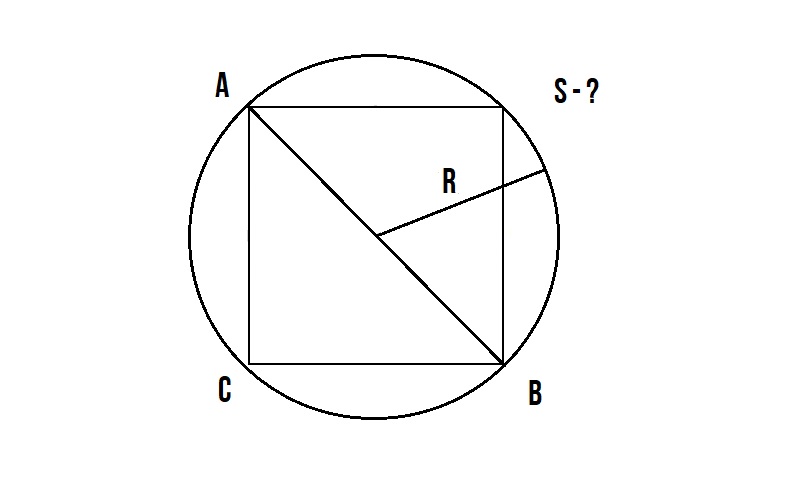
  • Как найти площадь квадрата зная радиус описанной окружности!?

    Задача :

    Как найти площадь квадрата зная радиус описанной окружности!?

    Данная задача такая же простая, как и выше описанная!

    У нас известен радиус окружности описанной вокруг квадрата.

    Диаметр окружности AB равен диагонали квадрата AB и мы знаем, что диаметр окружности равен двум радиусам d = 2R.

    По диагонали квадрата мы уже один раз высчитывали площадь здесь -> S = d²/2

    Далее подставляем S = (2R)²/2

    Как найти площадь квадрата зная радиус описанной окружности!?

  • Найти площадь квадрата онлайн

    Для того чтобы посчитать площадь квадрата онлайн, вам требуется в поле :

    Сторона квадрата – заполнить значением стороны квадрата.

    И нажать кнопку посчитать.

    Источник

    Калькулятор площади квадрата через диаметр вписанной окружности (круга)

    При помощи данного калькулятора можно вычислить площадь квадрата через диаметр вписанной окружности.

    Диаметр вписанной окружности в квадрат D

    Для того что бы вычислить площадь квадрата через диаметр вписанной окружности, нам необходимо понять какие общие параметры у диаметра вписанного круга и квадрата. И если обратить внимание на изображение вписанного квадрата, то можно заметить, что диаметр равен стороне квадрата.

    D = a

    Для вычисления площади квадрата нам необходимо длину стороны квадрата возвести в квадрат.

    Соответственно площадь квадрата вычисляется по следующей формуле:

    S = a*a = a2

    Где:
    S – площадь квадрата.
    a – сторона квадрата.
    D – диаметр круга.
    длина стороны квадрата = диаметру вписанной окружности (круга)

    Источник

    При помощи нашего калькулятора вы легко сможете узнать площадь вписанного в круг квадрата.

    Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.

    Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:

    1. либо площадь круга, обозначаемая буквой S,
    2. либо периметр круга, обозначаемый буквой P,
    3. либо радиус круга, обозначаемый буквой R,
    4. либо диаметр круга, обозначаемый буквой D.

    Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой

    c2 = 2a2,
    Таким образом
    a =

    √

    c2/2

    Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга

    D = c

    1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

    2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

    D=P/π

    3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

    D=2R

    Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,

    c=D

    мы можем узнать длину сторон квадрата используя теорему Пифагора

    после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.

    S = a2

    Источник

    Добавить комментарий