Онлайн калькулятор площади вписанного в круг квадрата. Как узнать площадь вписанного в круг квадрата.
Вычислить площадь вписанного квадрата через:
Радиус круга R:
Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
мы можем узнать длину сторон квадрата используя теорему Пифагора
после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.
Как определить площадь квадрата
О чем эта статья:
3 класс, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a 2 , где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d 2 : 2, где d — диагональ.
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r 2 , где r — это радиус вписанной окружности.
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R 2 , где R — это радиус описанной окружности.
У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р 2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Воспользуемся формулой: S = d 2 : 2.
Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .
Ответ: 4050 мм 2 .
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d
Диаметр окружности равен двум радиусам:
d = 2r
Получается, что сторона равна двум радиусам:
a = 2r
Используем формулу нахождения площади квадрата через сторону:
S = a 2
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2
Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2
Площадь квадрата через вписанную окружность
Как определить площадь квадрата
О чем эта статья:
3 класс, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a 2 , где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d 2 : 2, где d — диагональ.
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r 2 , где r — это радиус вписанной окружности.
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R 2 , где R — это радиус описанной окружности.
У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р 2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Воспользуемся формулой: S = d 2 : 2.
Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .
Ответ: 4050 мм 2 .
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d
Диаметр окружности равен двум радиусам:
d = 2r
Получается, что сторона равна двум радиусам:
a = 2r
Используем формулу нахождения площади квадрата через сторону:
S = a 2
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2
Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2
Онлайн калькулятор площади вписанного в круг квадрата. Как узнать площадь вписанного в круг квадрата.
Вычислить площадь вписанного квадрата через:
Радиус круга R:
Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
мы можем узнать длину сторон квадрата используя теорему Пифагора
после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.
Квадрат вписанный в окружность
Определение
Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.
На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.
Формулы
Радиус вписанной окружности в квадрат
- Радиус вписанной окружности в квадрат, если известна сторона:
Радиус вписанной окружности в квадрат, если известен периметр:
Радиус вписанной окружности в квадрат, если известна площадь:
Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:
Радиус вписанной окружности в квадрат, если известна диагональ:
Радиус описанной окружности около квадрата
- Радиус описанной окружности около квадрата, если известна сторона:
Радиус описанной окружности около квадрата, если известен периметр:
Радиус описанной окружности около квадрата, если известнаплощадь:
Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:
Радиус описанной окружности около квадрата, если известнадиагональ:
Сторона квадрата
- Сторона квадрата вписанного в окружность, если известнаплощадь:
Сторона квадрата вписанного в окружность, если известнадиагональ:
Сторона квадрата вписанного в окружность, если известен периметр:
Площадь квадрата
- Площадь квадрата вписанного в окружность, если известна сторона:
Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:
Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:
Площадь квадрата вписанного в окружность, если известен периметр:
Площадь квадрата вписанного в окружность, если известна диагональ:
Периметр квадрата
- Периметр квадрата вписанного в окружность, если известна сторона:
Периметр квадрата вписанного в окружность, если известна площадь:
Периметр квадрата вписанного в окружность, если известенрадиус вписанной окружности:
Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:
Периметр квадрата вписанного в окружность, если известна диагональ:
Диагональ квадрата
- Диагональ квадрата вписанного в окружность, если известна сторона:
Диагональ квадрата вписанного в окружность, если известна площадь:
Диагональ квадрата вписанного в окружность, если известен периметр:
Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:
Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности:
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/ploshad-kvadrata
http://b4.cooksy.ru/articles/ploschad-kvadrata-cherez-vpisannuyu-okruzhnost
[/spoiler]

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону

S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ

S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности

S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности

S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр

S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Расчёт площади квадрата через площадь окружности, вписанной в этот квадрат
Калькулятор рассчитывает площадь квадрата через площадь окружности вписанной в этот квадрат
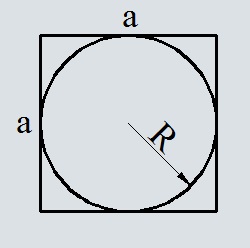
Введите площадь окружности Sокр
Формула площади квадрата через площадь окружности вписанной в этот квадрат
Где S – площадь квадрата,
Sокр – площадь окружности
Вывод формулы площади квадрата через площадь окружности вписанной в этот квадрат

Из формулы площади окружности выведем радиус
Сторона квадрата равна двум радиусам
Подставим в формулу площади квадрата
Подставим в формулу выведенный ранее радиус
Похожие калькуляторы
Калькулятор площади квадрата через диаметр вписанной окружности (круга)
При помощи данного калькулятора можно вычислить площадь квадрата через диаметр вписанной окружности.

Диаметр вписанной окружности в квадрат D
Для того что бы вычислить площадь квадрата через диаметр вписанной окружности, нам необходимо понять какие общие параметры у диаметра вписанного круга и квадрата. И если обратить внимание на изображение вписанного квадрата, то можно заметить, что диаметр равен стороне квадрата.
D = a
Для вычисления площади квадрата нам необходимо длину стороны квадрата возвести в квадрат.
Соответственно площадь квадрата вычисляется по следующей формуле:
S = a*a = a2
Где:
S – площадь квадрата.
a – сторона квадрата.
D – диаметр круга.
длина стороны квадрата = диаметру вписанной окружности (круга)
Читайте статью, чтобы знать, как находить площадь квадрата разными способами.
Содержание
- Как найти сторону квадрата, зная его площадь?
- Как найти диагональ квадрата, если известна его площадь?
- Как найти площадь квадрата через диагональ?
- Как найти площадь квадрата, зная его периметр?
- Как найти площадь квадрата вписанного в окружность с заданным радиусом?
- Как найти площадь квадрата описанного около окружности с заданным радиусом?
- Примеры решения задач на тему «Площадь квадрата»
- Видео: Вычисление площади квадрата
Квадрат — это равносторонний прямоугольник. У данного правильного и плоского четырехугольника равенство во всех сторонах, углах и диагоналях. Из-за того что существует такое равенство, формула для вычисления площади и других характеристик, немного видоизменяется по сравнению с иными математическими фигурами. Но это не делает задачи слишком сложными. Давайте разберем все формулы и решения задач в этой статье.
Как найти сторону квадрата, зная его площадь?
Площадь S прямого и квадратного угольников вычисляется по формуле: a умножить на b. Но так как у квадрата полное равенство сторон, то его площадь будет равна: S=(a) во второй степени. Как узнать величину стороны квадрата, зная его площадь?
- Если известна площадь квадратного угольника, то сторону находим путем исчисления площади из-под квадратного корня.
- К примеру, площадь угольника равна 49, то чему равняется сторона?
- 49=(а) во второй степени. Решение: а=корень из 49=7. Ответ: 7.
Если нужно найти сторону квадратного угольника, площадь которого состоит слишком длинного числа, тогда воспользуйтесь калькулятором. Наберите сначала число площади, а потом нажмите знак корня на клавиатуре калькулятора. Получившееся число и будет ответом.
Как найти диагональ квадрата, если известна его площадь?
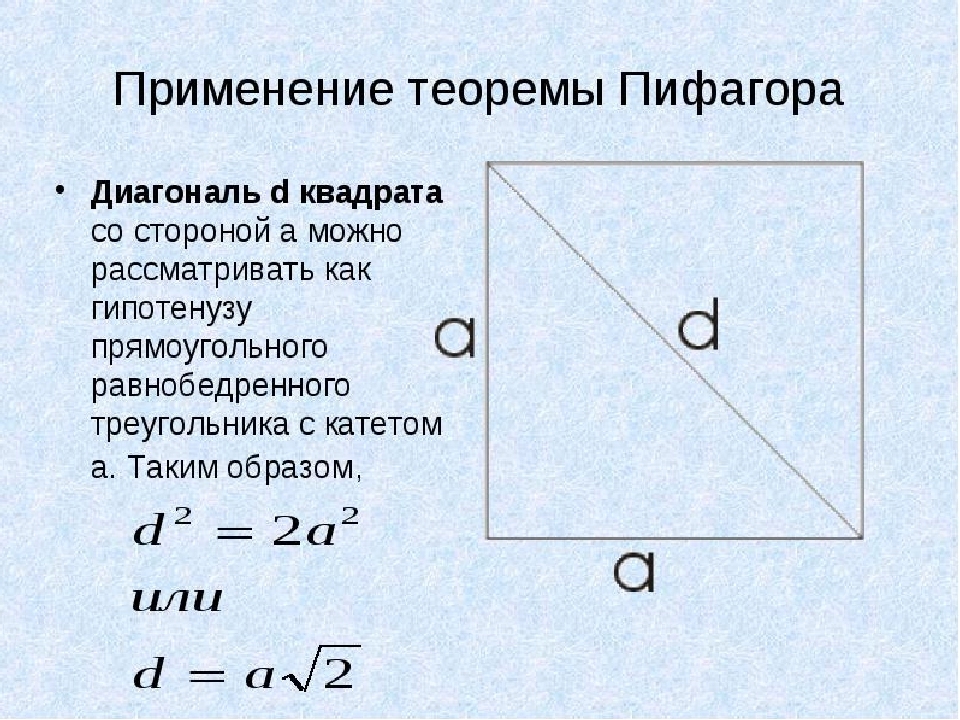
В этом примере будем использовать теорему Пифагора. У квадрата все стороны равны, а диагональ d мы будем рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Теперь находим диагональ квадрата, если известна его площадь:
- Чтобы не расписывать всю теорему Пифагора будем решать по второму варианту: d=a√2, где а — это сторона квадрата.
- Итак, нам известна площадь квадрата, например, она равна 64. Значит одна сторона а=√64=8.
- Получается d=8√2. Корень из 2 не получается целым числом, поэтому в ответе можно написать именно так: d=8√2. Но, если хочется вычислить значение, тогда воспользуйтесь калькулятором: √2= 1,41421356237 и умножьте на 8, получается 11, 3137084.
Важно: Обычно в математике не оставляют в ответе цифры с большим количеством чисел после запятой. Нужно округлять или оставить с корнем. Поэтому ответ на нахождение диагонали, если площадь равна 64 будет таким: d=8√2.
Как найти площадь квадрата через диагональ?
Формула нахождения площади квадрата через диагональ простая:
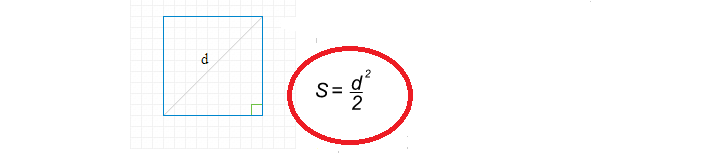
Теперь напишем решение по нахождению площади квадрата через диагональ:
- Диагональ d=8.
- 8 в квадрате равняется 64.
- 64 разделить на 2 равно 32.
- Площадь квадрата равна 32.
Совет: У этой задачи есть еще одно решение через теорему Пифагора, но оно более сложное. Поэтому используйте решение, которое мы рассмотрели.
Как найти площадь квадрата, зная его периметр?
Периметр квадратного угольника P — это сумма всех сторон. Чтобы найти его площадь, зная его периметр, нужно сначала вычислить сторону квадратного угольника. Решение:
- Допустим периметр равен 24. Делим 24 на 4 стороны, получается 6 — это одна сторона.
- Теперь используем формулу нахождения площади, зная чему равна сторона квадратного угольника: S=а в квадрате, S=6 в квадрате=36.
- Ответ: 36
Как видите, зная периметр квадрата, просто найти его площадь.
Как найти площадь квадрата вписанного в окружность с заданным радиусом?
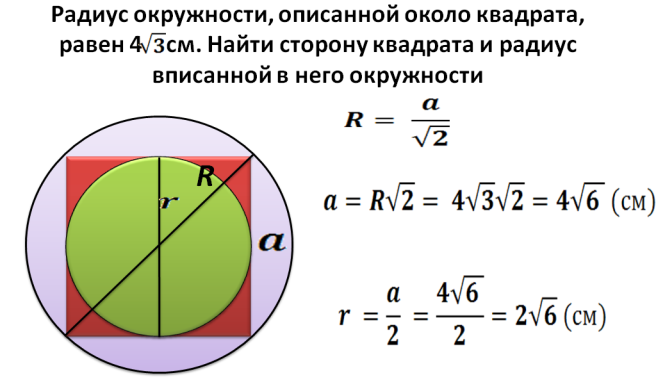
Радиус R — это половина диагонали квадрата, вписанного в окружность. Теперь можем найти диагональ по формуле: d=2*R. Далее находим площадь квадрата вписанного в окружность с заданным радиусом:
- Диагональ равна 2 умножить на радиус. Например радиус равен 5, тогда диагональ равна 2*5=10.
- Выше было описано, как находить площадь квадрата, если известна диагональ: S=диагональ в квадрате разделить на 2. S=10*10 и разделить на 2=50.
- Ответ — 50.
Эта задача немного сложнее, но тоже легко решаемая, если знать все формулы.
Как найти площадь квадрата описанного около окружности с заданным радиусом?
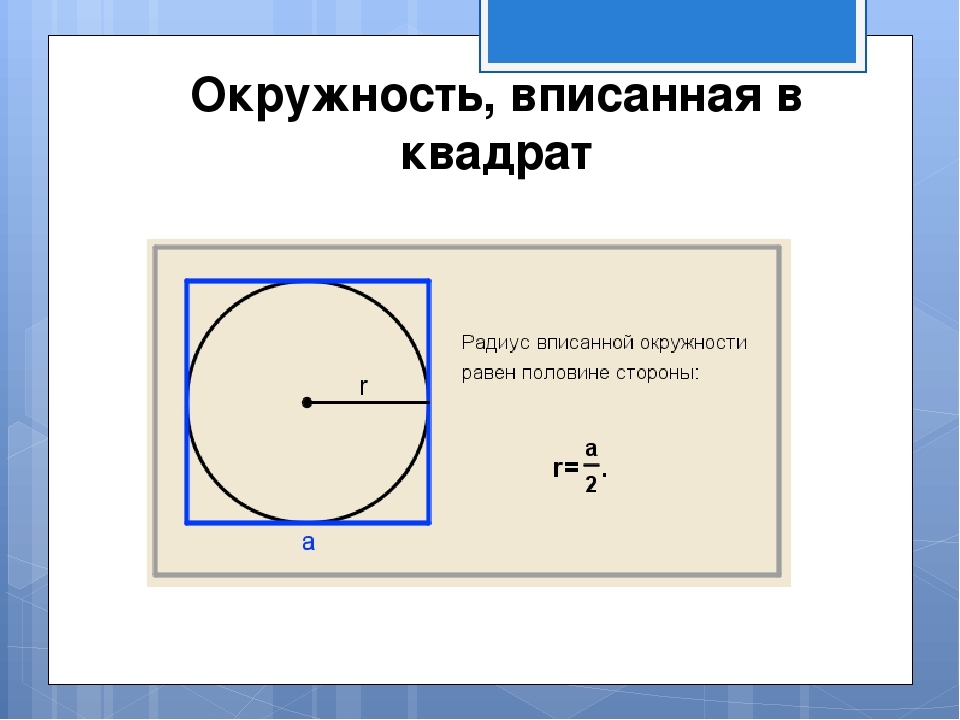
На картинке видно, что радиус вписанной окружности равен половине стороны. Сторона находится по формуле обратной той, которая изображена на картинке: а=2*r. Потом уже находим площадь квадрата описанного около окружности с заданным радиусом по формуле S=а в квадрате. Решение:
- Допустим, радиус равен 7. Сторона квадрата а равна 2*7=14.
- S=14 в квадрате=196.
Если понять суть решения подобных задач, то можно решать их быстро и просто. Давайте рассмотрим еще несколько примеров.
Примеры решения задач на тему «Площадь квадрата»
Чтобы закрепить пройденный материал и запомнить все формулы, необходимо решить несколько примеров задач на тему «Площадь квадрата». Начинаем с простой задачи и движемся к решению более сложных:



Теперь вы знаете, как пользоваться формулой площади квадрата, а значит, вам любая задача под силу. Успехов в дальнейшем обучении!
