Как рассчитать площадь квадрата
На данной странице калькулятор поможет рассчитать площадь квадрата онлайн. Для расчета задайте длину стороны или диагональ.
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба.
Через сторону
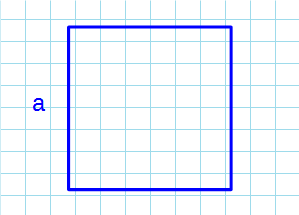
Формула для нахождения площади квадрата через сторону:
a – сторона квадрата.
Через диагональ
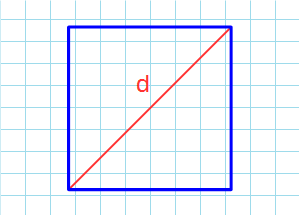
Формула для нахождения площади квадрата через диагональ:
d – диагональ квадрата.

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону
S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ
S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности
S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности
S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр
S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Что такое квадрат и понятие его площади
Квадрат — простейшая плоская геометрическая фигура. Является одновременно правильным четырёхугольником и прямоугольником, все стороны которого равны.
Состоит соответственно из четырёх равных сторон, четырёх вершин ABCD и прямых углов 90°.
Под площадью квадрата подразумевается пространство, ограниченное его сторонами (та часть плоскости, что внутри). Способов расчёта существует немного, а формулы для вычисления площади весьма простые.
Как найти площадь квадрата через сторону
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его сторон — введите его в соответствующее поле. В зелёном поле автоматически выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через периметр
Данный способ и калькулятор позволит найти площадь квадрата через значение его периметра — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через диагональ
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его диагонали — введите его в соответствующее поле. В зелёном поле получите результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус вписанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса вписанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус описанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса описанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат автоматически.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Ваша оценка?
[Оценок: 5 / Средняя: 4.6]
- Главная
- Справочник
- Как найти площадь квадрата
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь квадрата
Поможем сделать домашку Online
Первое занятие бесплатно
Перейти
Решение задачи по геометрии
Выполнение 1-3 дня
от 150 ₽
Заказать
Подробнее
Контрольные по геометрии
Выполнение 1–4 дня
от 310 ₽
Заказать
Подробнее
Контрольные по математике
Выполнение 1–4 дня
от 260 ₽
Заказать
Подробнее
Содержание:
- Формула
- Примеры вычисления площади квадрата
Формула
Чтобы найти площадь квадрата (рис. 1), надо длину его стороны возвести в квадрат, то есть
$$S=a^2$$
Напомним, что квадратом называется правильный четырехугольник, у которого все стороны и все углы равны.
Примеры вычисления площади квадрата
Пример
Задание. Найти площадь квадрата со стороной 3 см.
Решение. Площадь квадрата равна квадрату его стороны, то есть
$S=3^2=9$(см2)
Ответ. $S=3^2=9$ (см2)
Все формулы площади
Калькулятор площади квадрата

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Узнать стоимость
Пример
Задание. Найти площадь квадрата, диагональ которого равна 2 м.
Решение. Известно, что сторона
$a$ квадрата связана с его диагональю $d$ соотношением:
$$d=a sqrt{2}$$
тогда отсюда находим, что
$a=frac{d}{sqrt{2}}=frac{2}{sqrt{2}}=sqrt{2}$(м)
А тогда искомая площадь
$S=(sqrt{2})^{2}=2$ (м2)
Ответ. $S=2$ (м2)
Читать дальше: как найти площадь прямоугольника.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Поможем выполнить
любую работу
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Контрольные, курсовые, дипломные
Узнать подробнее
Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Краткая теория
- Формулы
- Теоремы
- Свойства
- Таблицы
Теоретический материал
- Формулы и свойства логарифмов
- Таблица интегралов
- Тригонометрические формулы
- Таблица степеней
- Формулы и свойства степеней
- Формулы площади
- Таблица Лапласа
- Формулы объема
Все еще сложно?
Наши эксперты помогут разобраться
Все услуги
Дипломные работы
Выполнение 2-3 недели
от 7000 ₽
Курсовые работы
Выполнение 5-7 дней
от 1500 ₽
Контрольные работы
Выполнение 1–4 дня
от 260 ₽
Написание рефератов
Выполнение 2-5 дней
от 650 ₽
Решение задач
Выполнение 1–3 дня
от 90 ₽
Написание диссертаций
Выполнение 2-3 месяца
от 19 000 ₽
Как найти площадь треугольника
Как найти площадь
Как найти площадь ромба
Как найти площадь эллипса
Не получается написать работу самому?
Доверь это кандидату наук!
Я даю согласие на обработку своих персональных данных в соответствии с Политикой
конфиденциальности и принимаю условия Договора публичной оферты
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
Прикрепить файл
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
|
Квадрат самая простая и красивая, после окружности конечно, геометрическая фигура. Для нахождения его периметра или площади надо всего лишь знать длину любой стороны – ведь у квадрата эти стороны одинаковые, да к тому же параллельны. Зная сторону квадрата его площадь находим как квадрат стороны: Периметр квадрата в этом случае равен длине четырех сторон или учетверенной длине одной стороны: Ну и наконец еще один способ определения площади квадрата – через его диагональ, которая по совместительству является гипотенузой прямоугольных равнобедренных треугольников, каждый из которых равен половине квадрата. Площадь квадрата через диагональ считается по формуле: автор вопроса выбрал этот ответ лучшим Winiki 2 года назад Начертив небольшой квадрат – дюжина на дюжину сантиметров, я как бы посмотрел на него со стороны и увидел для себя одно. Постоянные у него только углы – четыре угла по 90º. Если их поделить диагоналями, они уменьшатся вдвое – два по 45º. Но при измерении периметра и площади от них ничего не зависит. Всё напрямую зависит только от длины стороны (a). Значение это может быть не известно, но его можно без труда вычислить, зная длину диагонали (d). Таким образом мы можем выразить периметр (P) и площадь (S) через длины стороны или той самой диагонали квадрата. Всё так, но ведь на практике может сложиться такая ситуация, когда мы уже будем знать значение площади квадрата, а необходимо будет посчитать его периметр. Или, наоборот, потребуется вычислить значение площади, исходя из сведений о периметре. Стало быть для каждого из (P) и (S) нам потребуется определиться не с двумя, а с тремя формулами. Что же, давайте приступим. Только одно маленькое замечание: очень неудобно рисовать буквами знак “квадратный корень” и я предлагаю использовать функцию “Корень()”, как это делается в электронной таблице Excel, если вы не против. Тогда мы можем получить следующие записи формул: Периметр (P)
Площадь (S)
Вроде бы всё готово и можно было бы на этом остановиться. Но, друзья мои, как в таком деле обойтись без проверки? Я предлагаю подставить в качестве длины число 12, как в нашем квадрате на картинке. Тогда значение диагонали для него составит = Корень(2*a²) = 16,97. Тогда мы можем подставить эти данные в найденные формулы и получим следующие результаты: Вычисление через длину стороны:
Вычисление через длину диагонали:
Вычисление через площадь или периметр, соответственно:
Вот, теперь с чистой совестью можно отправляться на заслуженный отдых. И р и н а 6 лет назад Поскольку квадрат является геометрической фигурой, у которой все стороны равны, то для нахождения его площади достаточно знать длину всего одной его стороны. Как известно, чтобы найти площадь квадрата, нужно значение одной его стороны возвести в квадрат. Формула площади квадрата может выглядеть, например, вот так: , где S – площадь, а – сторона квадрата. Периметр квадрата равен сумме длин всех его сторон, а мы знаем, что у квадрата четыре стороны, значит просто берем длину одной из сторон квадрата и умножаем ее на четыре, так как это количество сторон. Формула нахождения периметра квадрата: ,где Р – обозначение периметра, а – длина стороны квадрата. Елена Шамсиева 9 лет назад Эти формулы мне сейчас проше вывести, чем вспомнить. У квадрата 4 грани или стороны. Если длину каждой из них назвать например, буквой h, то не долго думая можно записать формулы расчета: Площадь (S), прямоугольника любого равна произведению высоты на ширину, а квадрат- это и есть прямоугольник, у которого Высота равна ширине, то есть S=h*h= h в квадрате. Периметр (P) любого многоугольника- это сумма длин всех его сторон, у квадрата 4 стороны длиной h, то есть его периметр P= 4h Oleg74 8 лет назад Очень простой вопрос из курса школьной программы, ведь многие точно знают, как определить площадь и периметр квадрата, тем более, что у квадрата все стороны равны. Итак, площадь квадрата :
Периметр квадрата – это сумма всех четырех сторон квадрата :
88SkyWalker88 8 лет назад Периметром любой фигуры называют сумму длин всех его сторон. Как известно, у квадрата все стороны равны. Следовательно, чтобы найти периметр, достаточно длину одной стороны умножить на четыре. Формула такая: P = 4a, а – это длина стороны квадрата. Можно просто сложить все стороны. P = a + a + a + a Каролина Мельникова 9 лет назад S=a2 ,Р=4а. Других формул для нахождения площади не знаю)можно попробовать через площадь двух прямоугольных треугольников,проведя диагональ.Sпрямоугольного треугольника=половина произведения катетов,т.е. S=а2/2 Ksyusha26 8 лет назад Площадь квадрата, насколько я помню, находится достаточно просто. Для этого необходимо знать, сколько составляет сторона квадрата. И это число возвести в квадрат. Чтобы найти периметр квадрата, нужно сложить все его стороны, либо же попросту одну сторону умножить на 4 Чосик более года назад Периметр – это сумма длин всех сторон. Потому можно посчитать для квадрата периметр двумя способами:
Если речь о площади, то методов также несколько:
У квадрата все стороны равны. Это значит,что нужно знать,чему равна одна сторона и данное число просто возвести в квадрат, т.е. число умножить на само себя. Все! Это мы узнали площадь. Теперь о периметре. Точно также узнаем,чему равна сторона квадрата и умножаем данное число на 4.(стороны потому что 4 у квадрата. Знаете ответ? |