Рассмотрим фигуру ниже:
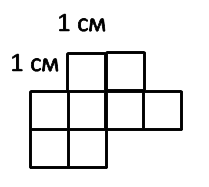
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.
Площадь одного такого квадрата называют квадратным сантиметром и записывают:
1 см2.
Площадь всей фигуры 8 см2.
Запомните!
![]()
Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.
В математике для нахождения площади геометрических фигур используют специальные формулы,
в которых площадь обозначается заглавной латинской буквой «S».
Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.
Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата,
равна 1 м, то его площадь равна 1
квадратному метру (1 м2); если длина
его стороны равна 1 см, то его площадь
равна 1 квадратному сантиметру
(1 см2).
Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.
Как перевести квадратные единицы
Рассмотрим квадрат со стороной 1 см.
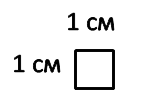
Его площадь равна:
S = 1 см · 1 см = 1см2
Рассмотрим квадрат со стороной 1 м.
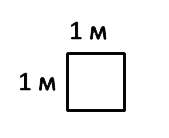
Его площадь равна:
S = 1 м · 1 м = 1 м2
Известно, что: 1 м = 100 см
1 м2 = 1 м · 1 м = 100 см · 100 см = 10 000 см2
Увеличим сторону квадрата равную 1 м в
10 раз. Получим квадрат со
стороной 10 м.
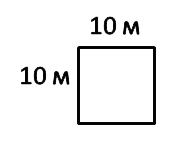
Площадь такого квадрата называют ар или сотка.
S = 10 м · 10 м = 100 м2
В одном аре — сто квадратных метров.
Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».
1 ар (сотка) = 100 м2
Чтобы выразить ар в cм2, вспомним, что 1 м2 = 10 000 см2.
Значит: 1 ар (сотка) = 100 м2 = 100 · 10 000 см2 = 1 000 000 см2
Увеличим сторону квадрата равную 10 м в 10 раз.
Получим квадрат со
стороной 100 м.
Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование
проговаривается полностью.
Выразим гектар в квадратных метрах.
1 га = 100 м · 100 м = 10 000 м2
Теперь определим, сколько в одном гектаре аров.
1 ар = 100 м2
Значит: 10 000 м2 : 100 м2 = 100 (ар)
1 га = 100 ар
Для измерения больших площадей, например, территорий государств, материков используют квадратный километр.
То есть квадрат со стороной 1 км и
площадью 1 км2.
1 км = 1000 м
1 км2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м2
Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.
Таблица переводов квадратных единиц
Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.
| га | ар | м2 | cм2 | |
|---|---|---|---|---|
| 1 км2 | 100 га | 10 000 ар | 1 000 000 м2 | 1 000 000 000 cм2 |
| 1 га | 1 га | 100 ар | 10 000 м2 | 100 000 000 cм2 |
| 1 ар | 0,01 га | 1 ар | 100 м2 | 1 000 000cм2 |
| 1 м2 | 0,000 1 га | 0,01 ар | 1 м2 | 10 000 cм2 |
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
12 сентября 2018 в 20:57
Дмитрий Мозговой

Профиль
Благодарили: 0
Сообщений: 1

Дмитрий Мозговой
Профиль
Благодарили: 0
Сообщений: 1
Внутри большего квадрата расположен меньший квадрат площади 73. Известно, что длины отрезков, на которые сторона большего квадрата делится вершинами меньшего квадрата, — натуральные числа. Чему равна площадь большего квадрата?
0
Спасибо
Ответить
14 октября 2018 в 20:45
Ответ для Дмитрий Мозговой
Дарья Тихая

Профиль
Благодарили: 0
Сообщений: 1

Дарья Тихая
Профиль
Благодарили: 0
Сообщений: 1
146
0
Спасибо
Ответить
21 октября 2018 в 15:44
Ответ для Дмитрий Мозговой
Владимир Шварцман

Профиль
Благодарили: 0
Сообщений: 1

Владимир Шварцман
Профиль
Благодарили: 0
Сообщений: 1
Пусть отрезки большего квадрата a и в. Тогда а2 + в2 =73 Сумма двух чисел нечётна если одно чёт., а второе нечёт. Это 1,9,25,49 и 4, 16,36.64 Легко видеть, что это числа 9 и 64.Т.е. а=3 и в=8 Пл. большого квадрата=112 =121
0
Спасибо
Ответить
12 ноября 2018 в 3:31
Ответ для Дмитрий Мозговой
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Неверно.
0
Спасибо
Ответить
22 июня 2016 в 20:17
Клара Чукаева

Профиль
Благодарили: 0
Сообщений: 1

Клара Чукаева
Профиль
Благодарили: 0
Сообщений: 1
д вечер. у меня вопрос: как найти площадь таблички размером 50 см на 75 см? если перемножить, как нам предлагает школьная программа, то получается 3750 см2, разве это возможно? я ошибаюсь? напишите формулу для расчета пожалуйста?
0
Спасибо
Ответить
24 июня 2016 в 12:18
Ответ для Клара Чукаева
Павел Асафов

Профиль
Благодарили: 0
Сообщений: 2

Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
Здравствуйте! Все верно.
Формула площади прямоугольника S=a · b
(a)50 · (b)75=3750 см2
Может вы спутали с периметром? Периметр будет равен 250 см
a ·2+b · 2
0
Спасибо
Ответить
16 января 2016 в 18:29
Надюша Бисерова

Профиль
Благодарили: 0
Сообщений: 1

Надюша Бисерова
Профиль
Благодарили: 0
Сообщений: 1
ширина прамоугольника 23 см. на сколько увеличиться площадь прамоугольника, если его длину увеличить на 3 см?
подскажите решение пожалуйста
0
Спасибо
Ответить
21 января 2016 в 16:17
Ответ для Надюша Бисерова
Сергей Фадеев

Профиль
Благодарили: 0
Сообщений: 6

Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
на 3 см квадратных
если я не ошибаюсь взависимости от длины
0
Спасибо
Ответить
24 января 2016 в 13:50
Ответ для Надюша Бисерова
Инна Шабрашина

Профиль
Благодарили: 0
Сообщений: 5

Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
увеличится на 69
0
Спасибо
Ответить
12 октября 2015 в 17:22
Мося Мося

Профиль
Благодарили: 0
Сообщений: 1

Мося Мося
Профиль
Благодарили: 0
Сообщений: 1
найди площадь квадрата периметр которого 280см
0
Спасибо
Ответить
1 июля 2016 в 14:20
Ответ для Мося Мося
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для нахождения площади квадрата в данном случае нам понадобятся две формулу, а именно:
1) Формула периметра квадрата P=4a. Подробно про периметр читаем здесь http://math-prosto.ru/?page=pages/perimeter/perimeter.php
2) Формула площади квадрата S=a2. Подробно читать здесь http://math-prosto.ru/?page=pages/area/area_figures.php
Приступим к решению. Выразим сторону квадрата из формулы периметра:
P=4a
a=P: 4
a= 280: 4 = 70 (см)
Теперь воспользуемся формулой площади квадрата:
S=a2
S=702=4900 (см2)
Ответ: площадь квадрата равна 4900 см2
0
Спасибо
Ответить
4 сентября 2015 в 15:44
Игорь Винников

Профиль
Благодарили: 0
Сообщений: 2

Игорь Винников
Профиль
Благодарили: 0
Сообщений: 2
Площадь прямоугольника64мс2, одна из сторон 16см. Надо найти соседнюю сторону
0
Спасибо
Ответить
1 сентября 2016 в 10:18
Ответ для Игорь Винников
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Площадь прямоугольника рассчитывается по формуле S=a · b. Подставим значения в формулу и вычислим вторую сторону:
64=16 · b
b=64/16=4
вторая сторона равна 4.
проверка: 16 · 4 = 64.
Ответ: Соседняя сторона прямоугольника равна 4 см.
0
Спасибо
Ответить
6 июля 2015 в 17:48
Дмитрий Рыжков

Профиль
Благодарили: 0
Сообщений: 2

Дмитрий Рыжков
Профиль
Благодарили: 0
Сообщений: 2
Посмотрите, у вас не первый раз перепутаны буквы в примерах.Например посмотрите нм тему: площадь сложных фигур.там же треугольник обозначен одними буквами, а написано в примере другими совершенно. Никто не ответил по предыдущей теме.спасибо.
0
Спасибо
Ответить
12 июля 2015 в 13:31
Ответ для Дмитрий Рыжков
Борис Гуров

Профиль
Благодарили: 1
Сообщений: 27

Борис Гуров
Профиль
Благодарили: 1
Сообщений: 27
Здравствуйте, Дмитрий.
Благодарим Вас за указанное замечание.
Пожалуйста, укажите, более конкретно место ошибки.
В уроке «Площадь сложных фигур» мы не нашли ошибку, о которой Вы написали.
0
Спасибо
Ответить
17 мая 2015 в 10:59
Соня Кизилова

Профиль
Благодарили: 0
Сообщений: 1

Соня Кизилова
Профиль
Благодарили: 0
Сообщений: 1
Самостоятельная работа.
Задание 3.
На сколько частей разбивают плоскость 4 прямые, пересекающиеся в одное точке?
Задание 2.
Начертите угол MON. Отметьте точку K, лежащую внутри этого угла, и точку L, лежащую на отрезке NK.
Задание 4.
Постройте треугольник ABC со стороной AB= 6см,?ABC= 45градусов, ?BAC= 75 градусов.Помогите пожалуйста![]() …
…
0
Спасибо
Ответить
17 мая 2015 в 12:57
Ответ для Соня Кизилова
Ярослава Фесенко

Профиль
Благодарили: 0
Сообщений: 3

Ярослава Фесенко
Профиль
Благодарили: 0
Сообщений: 3
1.8 частей
0
Спасибо
Ответить
Загрузить PDF
Загрузить PDF
Определить площадь плоских фигур в квадратных сантиметрах (также обозначаемых как см2) достаточно просто. В самом легком случае, когда требуется рассчитать площадь квадрата или прямоугольника, она вычисляется произведением длины и ширины. Площадь других фигур (кругов, треугольников и так далее) можно определить с помощью целого ряда специальных математических формул. Также, если потребуется, можно без труда перевести площадь в квадратные сантиметры из других единиц измерения.
-

1
Определите длину измеряемой площади. У квадратов и прямоугольников по четыре стороны, расположенных под прямыми углами относительно друг друга. В случае с прямоугольниками, их противоположные стороны равны между собой, тогда как у квадратов равны все стороны. Измерьте одну из сторон квадрата или большую из сторон прямоугольника, чтобы определить ее длину в сантиметрах.[1]
-

2
Определите ширину измеряемой площади. Далее измерьте в сантиметрах любую из сторон, смежных с той, которую вы измерили в первую очередь. Эта сторона будет находиться под углом в 90 градусов к первой. Вторая мерка будет обозначать ширину квадрата или прямоугольника.[2]
- Так как у квадрата все стороны одинаковы, его длина будет равна ширине. Поэтому у квадрата можно изначально измерить только одну сторону.
-

3
Умножьте длину на ширину. Просто перемножьте длину и ширину фигуры, чтобы определить площадь квадрата или прямоугольника в квадратных сантиматрах.[3]
- Например, допустим, что длина прямоугольника составляет 4 см, а ширина – 3 см. В таком случае площадь фигуры рассчитывается следующим образом: 4 × 3 = 12 квадратных сантиметров.
- В случае с квадратом (по причине равных сторон) можно просто умножить саму на себя длину одной из его сторон (другими словами, возвести ее “в квадрат” или “во вторую степень”), чтобы определить площадь фигуры в квадратных сантиметрах.
Реклама
-

1
Найдите площадь круга по формуле: S = π × r2. Чтобы найти площадь круга в квадратных сантиметрах, необходимо знать расстояние в сантиметрах от центра круга до линии его окружности. Это расстояние называется радиусом окружности. Как только радиус будет известен, обозначьте его буквой r из вышеупомянутой формулы. Умножьте значение радиуса само на себя и на число π (3,1415926…), чтобы узнать площадь круга в квадратных сантиметрах.[4]
- Например, площадь круга с радиусом 4 см составит 50,27 квадратных сантиметра в результате перемножения 3,14 и 16.
-

2
Вычислите площадь треугольника по формуле: S = 1/2 b × h. Площадь треугольника в квадратных сантиметрах вычисляется умножением половины длины его основания b (в сантиметрах) на его высоту h (в сантиметрах). Основанием треугольника выбирается одна из его сторон, тогда как высота треугольника – это перпендикуляр, опущенный к основанию треугольника из противоположной к нему вершины. Площадь треугольника можно вычислить через длину основания и высоту по любой из сторон треугольника и противоположной к ней вершине.[5]
- Например, если длина основания треугольника составляет 4 см, а высота, проведенная к основанию – 3 см, площадь составит: 2 x 3 = 6 квадратных сантиметра.
-

3
Найдите площадь параллелограмма по формуле: S = b × h. Параллелограммы подобны прямоугольникам за одним исключением – их углы не обязательно равны 90 градусам. Соответственно, расчет площади параллелограмма производится аналогичным для прямоугольника способом: длина стороны основания в сантиметрах умножается на высоту параллелограмма в сантиметрах. За основание берут любую из сторон, а высота определяется длиной перпендикуляра к ней из противоположного тупого угла фигуры.[6]
- Например, если длина основания параллелограмма составляет 5 см, а его высота – 4 см, его площадь составит: 5 x 4 = 20 квадратных сантиметров.
-

4
Вычислите площадь трапеции по формуле: S = 1/2 × h × (B+b). Трапеция – это четырехугольник две стороны которого параллельны между собой, а остальные две – нет. Чтобы определить площадь трапеции в квадратных сантиметрах, необходимо знать три мерки (в сантиметрах): длину более длинной параллельной стороны B, длину более короткой параллельной стороны b и высоту трапеции h (определяемую как кратчайшее расстояние между ее параллельными сторонами по перпендикулярному к ним отрезку). Сложите между собой длины двух параллельных сторон, поделите сумму пополам и умножьте на высоту, чтобы получить площадь трапеции в квадратных сантиметрах.[7]
- Например, если более длинная из параллельных сторон трапеции равна 6 см, более короткая – 4 см, а высота – 5 см, площадь фигуры составит: ½ x (6+4) х 5 = 25 квадратных сантиметров.
-

5
Найдите площадь правильного шестиугольника: S = ½ × P × a. Приведенная формула верна только для правильного шестиугольника с шестью равными сторонами и шестью одинаковыми углами. Буквой P обозначается периметр фигуры (или произведение длины одной стороны на шесть, что справедливо для правильного шестиугольника). Буквой a обозначается длина апофемы – расстояние от центра шестиугольника до середины одной из его сторон (точки, расположенной посередине между двумя соседними вершинами фигуры). Перемножьте периметр и апофему в сантиметрах и поделите результат на два, чтобы найти площадь правильного шестиугольника.[8]
- Например, если у правильного шестиугольника шесть равных сторон по 4 см (то есть его периметр P = 6 x 4 = 24 см), а длина апофемы равна 3,5 см, то его площадь составит: ½ x 24 x 3,5 = 42 квадратных сантиметра.
-

6
Вычислите площадь правильного восьмиугольника по формуле: S = 2a² × (1 + √2). Для расчета площади правильного восьмиугольника (с восемью равными сторонами и восемью одинаковыми углами) нужно знать только длину одной из сторон фигуры в сантиметрах (обозначенной в формуле буквой “a”). Подставьте соответствующее значение в формулу и вычислите результат.[9]
- Например, если длина стороны правильного восьмиугольника равна 4 см, то площадь этой фигуры составляет: 2 х 16 x (1 + 1,4) = 32 x 2,4 = 76,8 квадратных сантиметров.
Реклама
-

1
Переведите все мерки в сантиметры, прежде чем производить расчет площади. Чтобы сразу рассчитать площадь в квадратных сантиметрах, необходимо подставлять все параметры в формулу расчета площади также в сантиметрах (это касается, длины, высоты, апофемы и так далее). Поэтому, если ваши исходные данные выражены в других единицах измерения (например, в метрах), сначала их следует перевести в сантиметры. Ниже приведены соотношения наиболее популярных единиц измерения.
- 1 метр = 100 сантиметров
- 1 сантиметр = 10 миллиметров
- 1 дюйм = 2,54 сантиметра
- 1 фут = 30,48 сантиметра
- 1 сантиметр = 0,3937 дюйма
-

2
Чтобы перевести площадь из квадратных метров в квадратные сантиметры, ее следует умножить на 10000 (то есть площадь одного квадратного метра в сантиметрах), или на произведение 100 см на 100 см. Если вы знаете площадь фигуры в квадратных метрах, ее можно перевести в квадратные сантиметры умножением на 10000.[10]
- Например, 0,5 квадратного метра = 0,5 x 10000 = 5000 квадратных сантиметров.
-

3
Чтобы перевести в квадратные сантиметры площадь, выраженную в квадратных дюймах, умножьте ее на 6,4516. Как уже упоминалось, 1 дюйм равен 2,54 сантиметра, тогда как квадратный дюйм составляет 6,4516 квадратных сантиметров (или 2,54 x 2,54). Таким образом, если вам необходимо конвертировать в квадратные сантиметры площадь, равную 10 квадратным дюймам, следует умножить 10 на 6,4516, и у вас получится 64,5 квадратных сантиметров.[11]
- Также следует упомянуть, что в одном гектаре содержится 10000 квадратных метров, тогда как каждый квадратный метр равен 10000 квадратных сантиметров. Поэтому, чтобы выразить один гектар в сантиметрах, следует умножить 10000 на 10000 и получится 100 миллионов квадратных сантиметров.
Реклама
Об этой статье
Эту страницу просматривали 153 706 раз.
Была ли эта статья полезной?
Математика, 4 класс
Урок № 13. Единицы площади – квадратный километр, квадратный миллиметр. Таблица единиц площади.
Перечень вопросов, рассматриваемых в теме:
-единица измерения площади – квадратный миллиметр
– единица измерения площади – квадратный километр
– единицы измерения площади – ар и гектар
– таблица единиц измерения площади
Глоссарий по теме:
Площадь-это свойство фигур занимать место на плоскости.
Квадратный километр-единица измерения площади, равная площади квадрата со стороной 1м.
Квадратный миллиметр- единица измерения площади, равная площади квадрата со стороной 1мм.
Основная и дополнительная литература по теме урока:
- Математика: 4 класс: учебник в 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова.–М. Просвещение, 2016.с.39-42
- Всероссийские проверочные работы. Математика. Рабочая тетрадь 4 класс в 2 ч.Ч.1/ под. ред. Н. А. Сопруновой – М.; Просвещение, 2016. – с. 22-27
Теоретический материал для самостоятельного изучения
Сегодня мы будем говорить о единицах измерения площади.
За единицу измерения площади принимается квадрат со стороной, равной единице измерения длины

Вы уже знакомы с такими единицами площади, как квадратный сантиметр, квадратный дециметр и квадратный метр. Квадратными сантиметрами мы измеряем площадь небольших предметов, таких, как тетрадь. Квадратными дециметрами можно измерить площадь парты. Квадратными метрами измеряют площадь помещений – комнат, коридоров, залов.



см2 дм2 м2
А если надо будет вычислить площадь какой-нибудь страны.
Например, вычислить площадь России.
Ведь наша страна очень большая, и если измерять её в квадратных метрах, получится число гораздо больше миллиона. А это очень неудобно.
Для измерения больших площадей используют квадратный километр. Это площадь квадрата, сторона которого равна 1 км. Слова «квадратный километр» при числе сокращенно записывают так:1 км2
В квадратных километрах измеряют площади государств; так Россия занимает площадь более 17000000 км2, а Франция – 551000 км2
Но иногда надо измерить площади очень маленьких предметов. Единица измерения маленьких площадей – это квадратный миллиметр. Квадратный миллиметр – это площадь квадрата, сторона которого 1 мм.
Обозначается он так: 1 мм2.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Для измерения площади земельных участков оказалось удобным ввести промежуточные единицы 1 ар и 1 гектар.

1 ар – это квадрат со стороной 10 м, значит его площадь равна
1 а = 10 м ∙ 10 м = 100 м2.
Поскольку 1 ар равен 100 квадратным метрам, то эту единицу площади часто называют соткой.
1 гектар – это квадрат со стороной 100 м ,значит его площадь равна
1 га = 100м ∙ 100м = 10000м2
Вот теперь вы можете составить таблицу единиц площади. А помогут вам знание таблицы единиц длины и умение находить площадь квадрата.
1 см2 = 100 мм2
1 см2 = 10 мм2 ∙ 10 мм2 = 100 мм2
1 дм2 = 100 см2
1 дм2 = 10 см2 ∙ 10 см2 = 100 см2
1 м2 = 100 дм2
1 м2 = 10дм2 ∙ 10 дм2 = 100 дм2
1 дм2 = 10000 мм2
1 дм2 = 100 мм2 ∙ 100 мм2 = 10000 мм2
1 м2 = 10000 см2
1 м2 = 100см2 ∙ 100 см2 = 10000 дм2
Теперь внимательно рассмотрите таблицу и постарайтесь ее запомнить.

Задания тренировочного модуля:
1. Установите правильные соотношения
1 см2 100 дм2
1 м2 100 см2
1 дм2 1000000 м2
1 км2 100 мм2
Правильный ответ.
1 см2 100 дм2
1 м2 100 см2
1 дм2 1000000 м2
1 км2 100 мм2
2. Укажите какими единицами площади, ты будешь измерять
1. Площадь Евразии – квадратный__________________
2. Площадь цветка незабудки – квадратный___________
3. Площадь тетради – квадратный __________________
Правильный ответ.
1. Площадь Евразии – квадратный километр
2. Площадь цветка незабудки – квадратный миллиметр
3. Площадь тетради – квадратный сантиметр
Формулы площади геометрических фигур
Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника

-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p – a)(p – b)(p – c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,p = a + b + c – полупериметр треугольника. 2
Формулы площади квадрата

-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.
Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.
Формулы площади параллелограмма

-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d1, d2 – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.
Формулы площади ромба

-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d1, d2 – длины диагоналей.
Формулы площади трапеции

-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a – b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,p = a + b + c + d – полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника

-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S – площадь четырехугольника,
d1, d2 – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-

Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p – a)(p – b)(p – c)(p – d) – abcd cos2θ
где S – площадь четырехугольника,
a, b, c, d – длины сторон четырехугольника,
p = a + b + c + d2 – полупериметр четырехугольника,
θ = α + β2 – полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p – a)(p – b)(p – c)(p – d)
Формулы площади круга

-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.
Формулы площади эллипса
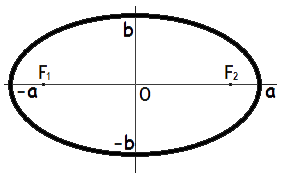
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S – Площадь эллипса,
a – длина большей полуоси эллипса,
b – длина меньшей полуоси эллипса.
