Как найти площадь луночек

Гиппокра́товы лу́ночки — серповидные фигуры, указанные Гиппократом Хиосским, ограниченные дугами двух окружностей.
Их особенность состоит в том, что эти фигуры можно квадрировать, то есть с помощью циркуля и линейки можно построить равновеликие им прямоугольники.
Гиппократ надеялся на этом пути решить проблему «квадратуры круга», однако существенного прогресса не добился.

Простейший пример[править | править код]

Простейший пример показан на рисунке.
Луночка ограничена двумя дугами — полуокружностью с диаметром на гипотенузе равнобедренного прямоугольного треугольника
и дугой окружности с центром в .
При этом площадь заштрихованной луночки равна площади .

Действительно, площадь полукруга с диаметром , равна площади сектора на дуге с центром .
Следовательно, площадь луночки равна площади треугольника .

Классификация[править | править код]

Гиппократ получил три квадрируемые луночки. Даниил Бернулли в «Математических упражнениях» (1724) указал условие (см. нижеприведенные отношения углов), которому должны удовлетворять алгебраически квадрируемые луночки, и привёл уравнение, дающее четвёртую квадрируемую луночку^[1]. Немного позднее финский математик Валлениус (1766) и независимо от него Леонард Эйлер (1771) тоже обнаружили ту же четвёртую и в дополнение к ней ещё одну, пятую луночку^[2]. В 1840 году Томас Клаузен независимо обнаружил и исследовал те же два негиппократовых типа квадрируемых луночек.

Позднее, в 1930-е годы, Н. Г. Чеботарёв и А. В. Дороднов доказали, что если угловые меры внешней и внутренней дуг луночек соизмеримы, то других типов квадрируемых луночек, кроме указанных пяти, не существует^[3]. Если обозначить угловые меры внешней и внутренней дуг луночек символами , то пяти типам квадрируемых луночек соответствуют следующие отношения .

• (Луночки Гиппократа) Углы: (180°:90°), (160,9°:107,2°), (205,6°:68,5°).
• (Прочие) Углы: (234.4°:46.9°) и (168.0°:100.8°).

Примечания[править | править код]

Литература[править | править код]

• Белозеров С. Е. Пять знаменитых задач древности. История и современная теория. — Ростов: изд-во Ростовского университета, 1975. — 320 с.
• Буницкий Е. Способ построения группы луночек, сумма которых квадрируется // В.О.Ф.Э.М.. — 1893. — № 175. — С. 159—161.
• Чеботарев Н. Г. Основы теории Галуа, Часть 1. М.: Эдиториал УРСС, 2004, 224c. ISBN 5-354-00941-3.

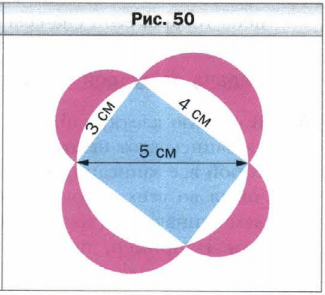
Задача Гиппократа. (Гиппократ Хиосский − древнегреческий геометр (V в. до н.э.).) Докажите, что сумма площадей закрашенных фигур (“луночек”) равна площади прямоугольника (рис.50).

Category:

• История
• Cancel

Криволинейные двуугольники (луночки Гиппократа)

Криволинейный (дуговой) двуугольник – фигура, образованная дугами двух окружностей.

.

Мы будем называть такой двуугольник луночкой.Частным случаем дуговых двуугольников являются луночки Гиппократа – фигуры, указанные Гиппократом Хиосским (V в. до н. э.), каждая из которых ограничена дугами двух окружностей и для каждой из которых с помощью циркуля и линейки можно построить равновеликие многоугольники. С помощью этих луночек Гиппократ  пытался справиться с одной из знаменитых задач древности – квадратурой круга. Одну из его луночек можно построить следующим образом: возьмем четверть круга и на хорде АС, соединяющей концы радиусов ОА и ОС, опишем как на диаметре внешнюю по отношению к четверти круга полуокружность.

Легко показывается, что площадь луночки равна площади треугольника АВС. Таким образом, луночка квадрируема.
Другая интерпретация этой же задачи на следующем рисунке

Гиппократ заметил, что суммарная площадь зеленых луночек равна площади квадрата, окрашенного здесь в красный цвет. Действительно, сумма площадей полукругов, построенных на сторонах этого квадрата, равна площади круга, в который вписан квадрат. Если из полукругов удалить окрашенные в черный цвет сегменты, то останутся четыре луночки; если же удалить их из большого круга, то останется квадрат.
Гиппократ получил три квадрируемые луночки. Д. Бернулли в “Математических упражнениях” указал условие, которому должны удовлетворять алгебраически квадрируемые луночки, и привел уравнение, дающее четвертую квадрируемую луночку.
Однако луночки Гиппократа задачу о квадратуре круга вперед к решению не продвинули: в 30—40-х годах XX в. И. Г. Чеботаревым и А. В. Дородновым доказано, что существует пять видов квадрируемых луночек, но они не квадрируемы вместе с кругом.
Следующее предложение  доказано арабом Ибн Альхаитамом, а французские математики А. де Лион и Г. Парди высказали его вновь в 1654 и в 1671 г.
Построим на гипотенузе прямоугольного треугольника как на диаметре полуокружность, лежащую с той же стороны гипотенузы, что и сам треугольник, а на катетах, как на диаметрах, построим полуокружности во внешнюю от треугольника сторону.
Тогда сумма площадей двух получившихся луночек равна площади треугольника АВС.

Здесь интересен еще и следующий факт – луночки являются равноширинными. Диаметры наибольших вписанных в них окружностей равны одной и той же величине, а именно половине разности между суммой катетов и гипотенузой треугольника.

Вот еще один интересный факт, являющийся частным случаем задачи о трех арбелонах. На сторонах прямоугольного теугольника, как на диаметрах, построены три окружности. Они образуют две луночки (выделены оранжевым) и арбелон (выделен серым), а также дуговой двуугольник, обозначенный буквой Т.

Оказывается, что сумма площадей луночек и арбелона без площади криволинейного двуугольника Т равна удвоенной площади треугольника АВС.
Следующий рисунок иллюстрирует еще одну теорему Гиппократа.

Пусть нижнее основание трапеции является диаметром описанной около нее окружности, АВ=ВС=CD и на боковых сторонах и верхнем основании, как на диаметрах построены полуокружности. При этом образуются три равные луночки (выделены серым). Оказывается, площадь трапеции равна сумме площадей этих луночек и полукруга (полукруг равен тем полукругам, из которых образованы луночки).
Написано на основе статьи Березин В.Н. Луночки Гиппократа (журнал Квант 1971, №5).
Рисунки сделаны с помощью программы Живая Геометрия.

Глава 1. Кто такой Гиппократ? 5 стр.

1. Гиппократ в медицине. 5 стр.
2. Гиппократ в астрономии 6 стр.
3. Гиппократ в геометрии 7 стр.

Актуальность:

Искусство построения геометрических фигур при помощи циркуля и линейки было в высокой степени развито в Древней Греции. Однако древним геометрам никак не удавалось выполнить некоторые построения, используя лишь циркуль и линейку, а построения, выполненные с помощью других инструментов, не считались геометрическими. К числу таких задач относятся так называемые три знаменитые классические задачи древности: о квадратуре круга, о трисекции угла, об удвоении площади круга.

Я считаю эту тему актуальной, потому что очень полезно изучать методы решений данных задач древними учёными, так как большинство методов и способов решений различных задач сохранились и до наших дней и используются в современной математике.

Я хотела больше узнать о возможных способах решения этих задач древними учёными, которые могли использовать только подручные материалы для решения такого рода задач.Тема квадратуры круга была актуальна уже за две тысячи лет до н. э. в Древнем Египте и Вавилоне. В то время у египетских математиков находятся первые решения задачи, как построить квадрат, равновеликий данному кругу. Однако решение не поддавалось их усилиям. Известный математик древности Гиппократ Хиосский (ок. 400 г. до н.э.) первый указал на то, что площадь круга пропорциональна квадрату его диаметра.

Цель реферата:

Задачи реферата:

1.Изучить литературу и источники Интернет по данной теме.

2. Ознакомиться с биографией Гиппократа и его открытиями в области медицины, астрономии, геометрии.

3. Изучить задачу о квадратуре круга

Глава 1 Кто такой Гиппократ

Гиппократ Хиосский ( Ίπποκράτης), вторая половина V века до н. э.

Гиппократ в медицине.

В трудах Гиппократа, ставших основой дальнейшего развития клинической медицины, отражены представление о целостности организма; индивидуальный подход к больному и его лечению; понятие об анамнезе; учения об этиологии, прогнозе, темпераментах.

Гиппократ родился на острове Кос (архипелаг Южные Спорады, юго-восток Эгейского моря) в семье потомственных врачевателей, возводивших свою родословную к Асклепию — богу медицины. В течение своей жизни Гиппократ много путешествовал, объездил Грецию, Малую Азию, побывал в Ливии и Тавриде, основал на родине медицинскую школу.

Задачу врача Гиппократ видел в изучении индивидуальных особенностей больного, в обеспечении мобилизации сил организма для восстановления здоровья. В медицинской этике Гиппократ, выдвинул четыре принципа лечения: не вредить больному; противоположное лечить противоположным; помогать природе; щадить больного.

Гиппократ в астрономии.

Гиппократ в геометрии.

Основная научная заслуга Гиппократа — составление первого полного свода геометрических знаний. Он назвал его Начала, основав тем самым традицию, которой позже следовали Евклид и многие другие учёные. Ван дер Варден предполагает, что Гиппократовы Начала охватывали материал примерно в объёме I—IV книг Начал Евклида.

Несколько отрывков этого труда дошли до наших дней в комментариях Симпликия (VI век н. э.) к Аристотелю. Здесь исследуются так называемые Гиппократовы луночки — серповидные фигуры, ограниченные двумя дугами окружностей. С помощью таких луночек Гиппократ пытался решить проблему квадратуры круга. Он нашёл три вида луночек, для которых можно построить равновеликий квадрат, но решить задачу в общем виде ему не удалось. В XIX веке было доказано, что с помощью циркуля и линейки квадрировать круг невозможно.

Гиппократ занимался также другой знаменитой задачей древности — удвоением куба. Он свёл её к задаче на вставку между двумя данными отрезками двух средних в непрерывной пропорции.

Глава 2 Задача о квадратуре круга

Одной из древнейших и самых популярных математических задач, занимавшей умы людей на протяжении 3 – 4 тысячелетий, является задача о квадратуре круга, т.е. о построении с помощью циркуля и линейки квадрата, равновеликому данному кругу.

Если обозначить радиус круга через r, то речь будет идти о построении квадрата, площадь которого равна πr 2 , а сторона равна r. Теперь известно, что число π – отношение окружности к своему диаметру – число иррациональное. Оно выражается бесконечной непериодической десятичной дробью 3,1415926… и было, между прочим, вычислено с 707 десятичными знаками математиком В. Шенксом. Этот результат вместе с формулой вычислений он обнародовал в 1837 году. Ни одна ещё задача подобного рода не решалась с таким огромным приближением и с точностью, далеко превышающее отношение микроскопических расстояний к телескопическим.

Шенкс вычислял. Следовательно, он стоял в противоречии с требованиями задачи о квадратуре круга, где требовалось найти решение построением. Работа, сделанная Шенксом, в сущности бесполезна – или почти бесполезна. Но, с другой стороны, она может служить довольно убедительным доказательством противного тому, кто, убедившись доказательствами Линдеманна и других или не зная о них, до сих пор ещё надеется, что можно найти точное отношение длины окружности к диаметру. Можно вычислить приближенное значение π (и корня квадратного из π), удовлетворяющее тем или иным практическим потребностям. Однако не в практическом отношении интересовала людей задача о квадратуре круга, а интересовала её принципиальная сторона: возможно ли точно решить эту задачу, выполняя построения с помощью только циркуля и линейки.

Возьму линейку, проведу прямую,

И мигом круг квадратом обернётся,

Посередине рынок мы устроим,

А от него уж улицы пойдут –

Ну, как на Солнце! Хоть оно само

И круглое, а ведь лучи прямые.

Эти стихи говорят о том, что задача уже была к тому времени очень популярна в Греции. Один из современников Сократа – софист Антифон считал, что квадратуру круга можно осуществить следующим образом: впишем в круг квадрат и, разделяя пополам дуги, соответствующие его сторонам, построим правильный вписанный восьмиугольник, затем шестнадцатиугольник и так далее, пока не получим многоугольник, который в силу малости сторон сольётся с окружностью. Но так как можно построить квадрат равновеликий любому многоугольнику, то и круг можно квадрировать. Однако уже Аристотель доказал, что это будет только приближённое, но не точное решение задачи, так как многоугольник никогда не может совпасть с кругом.

Фигуры-мениски ALBM и ADCE, ограниченными круговыми дугами, и называются луночками.

По теореме Пифагора:

Отношение площадей кругов или полукругов BMAEC и AECD равно, как впервые доказал сам Гиппократ, отношению квадратов соответствующих диаметров , которые в силу (1) равно 2. Итак, площадь сектора OAC равна площади полукруга, построенного на диаметре AC. Если из обеих этих равных площадей вычесть площадь сегмента ACE, то и получим, что площадь треугольника AOC равна площади луночки ADCE, или сумма площадей обеих луночек равна площади равнобедренного треугольника BCA. Гиппократ нашёл и другие луночки, допускающие квадратуру, и продолжал свои изыскания в надежде дойти до квадратуры круга, что ему, конечно, не удалось.

Различные другие попытки, продолжавшиеся в течение тысячелетий, найти квадратуру круга оканчивались неудачей. Лишь в 80-х годах 19века было строго доказано, что квадратура круга с помощью циркуля и линейки невозможна. Задача о квадратуре круга становится разрешимой, если применять, кроме циркуля и линейки, еще и другие средства построения. Так, еще в 4веке до н.э. греческие математики Динострат и Менехм пользовались для решения задачи одной кривой, которая была найдена еще в 5веке до н.э. Гиппием Элидским. Однако ученых Древней Греции и их последователей такие решения, находящиеся за пределами применения циркуля и линейки, не удовлетворяли. Будучи сначала чисто геометрической задачей, квадратура круга превратилась в течение веков в исключительно важную задачу арифметико-алгебраического характера, связанную с числом , и содействовала развитию новых понятий и идей в математике.

Квадратура круга — задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу. Эта задача является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки. Математика древности знала ряд случаев, когда с помощью этих инструментов удавалось преобразовать криволинейную фигуру в равновеликую ей прямолинейную (например, гиппократовы луночки). Попытки решения задачи о квадратуре круга, продолжавшиеся в течение тысячелетий, неизменно оканчивались неудачей. С 1775 года Парижская Академия наук, а затем и другие академии стали отказываться от рассмотрения работ, посвященных квадратуре круга. В 19 веке было дано научное обоснование этого отказа: строго установлена неразрешимость квадратуры круга с помощью циркуля и линейки.

Если принять за единицу измерения радиус круга и обозначить x длину стороны искомого квадрата, то задача сводится к решению уравнения: , откуда: .Как известно, с помощью циркуля и линейки можно выполнить все 4 арифметических действия и извлечение квадратного корня; отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины . Таким образом, неразрешимость этой задачи следует из неалгебраичности числа , которая была доказана в 1882 году Линдеманом.

Однако эту неразрешимость следует понимать, как неразрешимость при использовании только циркуля и линейки. Задача о квадратуре круга становится разрешимой, если, кроме циркуля и линейки, использовать другие средства. Простейший механический способ предложил Леонардо да Винчи. Изготовим круговой цилиндр с радиусом основания и высотой , намажем его чернилами и прокатим по плоскости. За один полный оборот цилиндр отпечатает на плоскости прямоугольник площадью . Располагая таким прямоугольником, уже несложно построить равновеликий ему квадрат.

Глава 3 Луночки Гиппократа.

Гиппократовы луночки, три фигуры, указанные Гиппократом Хиосским, каждая из которых ограничена дугами двух окружностей и для каждой из которых с помощью циркуля и линейки можно построить равновеликие прямолинейные фигуры. Построение одной из гиппократовых луночек ясно из рисунка. Площадь заштрихованной гиппократовой луночки равна площади равнобедренного треугольника АВС. Другие гиппократовы луночки получаются более сложным путём.

В поисках решения квадратуры круга Гиппократ Хиосский нашёл квадратуры трёх так называемых гиппократовых луночек, которые мы рассмотрим в реферате.

Прежде всего, задача о квадратуре круга представляется совершенно естественной с точки зрения логики математического мышления. В самом деле, с одной стороны, имели круг как первую фигуру, с которой приходиться сталкиваться, когда получаешь в руки циркуль. С другой стороны, есть ещё одна совершенно естественная фигура – квадрат. Каждая из этих фигур имеет вполне определенную площадь. Но, тогда, ни одного математика не надо, очевидно, убеждать в том, что между двумя такими фигурами с одинаковыми площадями можно совершенно естественно протянуть мостик – преобразовать одну из них в другую. Поскольку же преобразовывать можно было только с помощью циркуля и линейки, то возникла задача о том, чтобы с помощью данных инструментов построить сторону квадрата, площадь которого равна площади данного круга. Но это и есть задача о квадратуре круга.

Гиппократ заметил, что суммарная площадь зеленых луночек равна площади квадрата, окрашенного здесь в красный цвет. Действительно, сумма площадей полукругов, построенных на сторонах этого квадрата, равна площади круга, в который вписан квадрат. Если из полукругов удалить окрашенные в черный цвет сегменты, то останутся четыре луночки; если же удалить их из большого круга, то останется квадрат.
Гиппократ получил три квадрируемые луночки. Д. Бернулли в “Математических упражнениях” указал условие, которому должны удовлетворять алгебраически квадрируемые луночки, и привел уравнение, дающее четвертую квадрируемую луночку.
Однако луночки Гиппократа задачу о квадратуре круга вперед к решению не продвинули: в 30—40-х годах XX в. И. Г. Чеботаревым и А. В. Дородновым доказано, что существует пять видов квадрируемые луночек, но они не квадрируемы вместе с кругом.
Построим на гипотенузе прямоугольного треугольника как на диаметре полуокружность, лежащую с той же стороны гипотенузы, что и сам треугольник, а на катетах, как на диаметрах, построим полуокружности во внешнюю от треугольника сторону.
Тогда сумма площадей двух получившихся луночек равна площади треугольника АВС.
Здесь интересен еще и следующий факт – луночки являются равноширинными. Диаметры наибольших вписанных в них окружностей равны одной и той же величине, а именно половине разности между суммой катетов и гипотенузой треугольника.
Вот еще один интересный факт, являющийся частным случаем задачи о трех арбелонах. (Арбелон, секирка, так наз. у Архимеда фигура, ограниченная полуокружностью и 2-мя меньшими полуокружностями: площадь. А=площади круга, диаметр которого среднее геометрическое диаметров малых кругов.). На сторонах прямоугольного треугольника, как на диаметрах, построены три окружности. Они образуют две луночки (выделены оранжевым) и арбелон (выделен серым), а также дуговой двуугольник, обозначенный буквой Т.
Оказывается, что сумма площадей луночек и арбелона без площади криволинейного двуугольника. Т равна удвоенной площади треугольника АВС.
Следующий рисунок иллюстрирует еще одну теорему Гиппократа.
Пусть нижнее основание трапеции является диаметром описанной около нее окружности, АВ=ВС=CD и на боковых сторонах и верхнем основании, как на диаметрах построены полуокружности. При этом образуются три равные луночки (выделены серым). Оказывается, площадь трапеции равна сумме площадей этих луночек и полукруга (полукруг равен тем полукругам, из которых образованы луночки).

Дано: АВСД – квадрат, АВ=4 см, АВ – диаметр круга, 4 малых круга равны.

Доказать: равна суммарная площадь зелёных луночек площади квадрата.

Доказательство: S АВСД = 4х4=16 см^2, рассмотрим прямоугольный треугольник АСД: АД=СД, угол АДС=90 градусов, по теореме Пифагора(квадрат гипотенузы равен сумме квадратов катетов) можно узнать длину отрезка АС : АД=ДС=4 cм => 4^2х2=х^2, х = √32 ~ 5,65 cм.

АС диаметр круга(чёрного)=> R = 5,65/2 = 2,825=> S круга = ПR^2 ~25 см^2

АВ диаметр круга => R = 4/2=2 см => S круга = ПR^2 = 2х3,14 = 6,28 см^2

Узнаём суммарную площадь зелёных луночек:

Общая S полукругов~25 cм^2

25-16=9 см^2(суммарная площадь чёрных полукругов)=> 25-9=16 cм^2

Суммарная площадь луночек = площади квадрата.

Итак, выполнив эту работу, я узнала много нового и интересного об одной из знаменитых классических задач древности, о людях, посвятивших себя решению данной задачи, познакомилась с историей возникновения задачи, методами ее решения. К своему удивлению , что великий врач Гиппократ, посвятил большую часть своей жизни открытию интереснейших геометрических фактов. Различные другие, продолжавшиеся в течение тысячелетий, попытки найти квадратуру круга оканчивались неудачей. Лишь в 80-х годах 19в. было строго доказано, что квадратура круга с помощью циркуля и линейки невозможна. Задача о квадратуре круга становится разрешимой, если применять, кроме циркуля и линейки, еще другие средства построения.

Но, несмотря на это, интерес к этой знаменитой задаче не пропадает и сегодня. Многие современные математики пытаются решить ее.

Мне было интересно узнать, что при попытках решить эти задачи было сделано огромное число открытий, имеющих гораздо больший интерес и значение, чем сами поставленные задачи.

Я думаю, что задача о квадратуре круга будет волновать умы современных и будущих поколений ученых.

С теми, кто не имел бы права с ними сидеть, женщины часто лежат. Станислав Ежи Лец
ещё >>

Гиппократ (460 – 377 гг. до н.э.) является самым известным врачом древности. Он совершил знаменательные открытия в сфере медицины и анатомии человека. Так, основными его достижениями были введение в лечение людей индивидуального подхода к каждому случаю, сбор истории развития болезни человека и наличие аналогичных случаев у его родственников (анамнез), составление прогноза течения заболевания. Кроме того, Гиппократ разработал также теорию о темпераментах людей.

Медицинские знания Гиппократ получал от отца, потомственного лекаря. Его семья вела свое происхождение от древнегреческого бога медицины Асклепия. На острове Кос, где он родился, существовала медицинская школа. Достоверных фактов о жизни этого знаменитого врачевателя осталось не так уж и много. Известно, что он много путешествовал по Азии, Греции, Ливии, где получал информацию о разных способах лечения болезней.

Перу Гиппократа принадлежат множество сочинений о болезнях, травмах и способах их лечения. Эти сочинения признавались лучшими трудами в области медицины на протяжении тысячелетий, вплоть до начала Эпохи Просвещения.

Основным отличием в деятельности Гиппократа от своих современников было выяснение им причин появления заболеваний у пациентов и выявлением связи недугов с воздействием окружающей среды, а не приписывание болезней воли богов. Он разработал гипотезу о наличии в организме человека 4 вида жидкостей (кровь, желчь, черная желчь и мокрота), нарушение баланса содержания которых приводит к появлению заболевания.

В медицине Гиппократ предложил 4основных правила лечения:

– не навредить пациенту;

Вариант 2

Из исторических источников известно, что Гиппократ появился на свет в 460 году до рождения Христова. Его отец был врачом-асклепиадом, при том потомственным. Именно он показывает ему, что возможна большая любовь к медицинским наукам, при этом отец стал его первым учителем, потом он обучался под надзором Демокрита и Горгия, которые являлись философами.

Основы учений

Благодаря историческим сводкам известно, что именно Гиппократ становится первым медиком, который отвергает теорию о том, что именно бог посылает болезни на человечество. Благодаря ему медицину возводят в ранг отдельной науки.

Он уверен, что все болезни являются следствием поведения человека, то как он питается, ведет себя, а также в каких природных условиях он живет.

Благодаря историческим источникам мы узнаем, что он определял свою принадлежность к Косской школе врачей. Все врачи, объединенные под эгидой этой школы, старались найти настоящую первопричину болезни или патологий. Они на протяжении долгого времени пристально наблюдали за больными людьми. При этом сами врачи организовывали специализированный режим для больного человека, он был уверен, что это помогало самоизлечению страдающих людей.

Достижения

Именно Гиппократ смог выделить разделения темпераментов. Но он утверждает, что поведение любого человека зависит от содержания в организме человека слизи, черной желчи и крови. Он смог предугадать, что именно движет человеком в основном его поведении.

Гиппократ показал, что существует понятие стадийности, все патологии являются постоянно прогрессирующими явлениями. Если стадия кризиса закончилась, то после этого человек либо погибал, либо начинал поправляться и полностью выздоравливал.

Врач описал большинство методов обследования пациентов. В то время врачи использовали совсем простые способы излечения врачей. Гиппократ в свое время провел достаточно исследований, которые смогли окружающим доказать, что излечить заболевания возможно, стоит только правильно проследить за течением болезни и найти момент, когда кризис миновал.

5, 8 класс. История. Биология

Гиппократ

Интересные ответы

С 1019 по 1054 года киевский престол занимал один из сыновей Владимира Великого – князь Ярослав, прозванный в народе Мудрым. Его политика была направлена, в общем, на культурное развитие государства и образованность народа

Каждый согласится, что работа должна представлять собой любимый труд, который интересен и увлекателен. Главное, относиться к работе с любовью и проводить рабочее место в приятном коллективе

Великий русский писатель Александр Сергеевич Пушкин является автором не только романов, пьес и стихов, известных по всему миру, но и создателем семи прекрасных драматических произведений, занимающих особое место в его творчестве.

Процесс развития экосистемы планеты земля шел очень долгой время, и многие животные прошлых веков давно вымерли, не оставив после себя потомство

Ромен Роллан (1866-1944 гг.) относится к всемирно известным писателям, являющимся помимо маститого французского прозаика еще и общественным деятелем

Год назад во время жаркого спора с коллегами я впервые услышала о луночках Гиппократа. Упомянуты они были скорее метафорически: кто-то в сердцах воскликнул, что не луночкам же Гиппократа вместо формулы Ньютона — Лейбница должны мы учить студентов на лекциях по интегральному исчислению! Хотя из контекста спора мне показалось, что луночки Гиппократа — это преданье старины глубокой, не связанное с современной математикой. И я из любопытства решила выяснить, о чем речь.

Оказалось, что за луночками Гиппократа скрывается история длиной в две с половиной тысячи лет, охватывающая самые разные страны и культуры — от берегов Эгейского моря до Альпийских гор и от Каира эпохи Фатимидов до Москвы советских времен. Особенно драматично история развивается в XX веке, а заканчивается уже в наши дни, в 2003 году.

Другой Гиппократ

Почему Гиппократ Хиосский (не тот, которого клятва) стал искать луночки, площадь которых легко вычислить? Дело в том, что он, как и многие математики до и после него, хотел найти простую формулу для площади круга. Если разбить круг на несколько удачно подобранных луночек, его площадь можно будет найти как сумму площадей этих луночек. Гиппократу удалось найти еще две подходящие луночки, но этого оказалось недостаточно, чтобы сложить полный круг. Тем не менее мысль Гиппократа заинтересовала последующие поколения математиков и поиск луночек продолжался на протяжении двух с лишним тысяч лет — разные математики пытались дополнить результаты Гиппократа и часто придумывали что-то совершенно новое и неожиданное.

Первая луночка

Гиппократ придумал три интересные криволинейные фигуры — луночки. Площадь луночки Гиппократа задается такой же простой формулой, как и площадь квадрата. Первая луночка строится так:

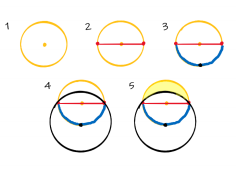
Сначала нужно построить окружность радиуса r (=жёлтая окружность на рисунке), отметить на ней концы какого-нибудь диаметра (=красный отрезок) и середину полуокружности (=синяя дуга), опирающейся на диаметр. Затем построить вторую окружность с центром в отмеченной середине дуги (черная точка) так, чтобы она прошла через отмеченные концы диаметра (красные точки). Окружности ограничивают два круга — поменьше и побольше. Луночка Гиппократа — это часть меньшего круга, которая лежит вне большего круга.

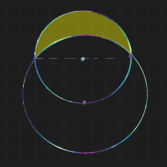
С астрономической точки зрения можно думать про меньший круг как про Луну, а про больший круг — как про тень от Земли во время неполного лунного затмения. Тогда луночка — это в точности освещенная часть Луны. Здесь читатель может остановиться и подумать над двумя вопросами. Как выразить площадь луночки через радиус r? И может ли месяц в какой-нибудь из лунных фаз совпасть по форме с луночкой Гиппократа? Ответ на первый вопрос будет дан ниже.

Площадь первой луночки

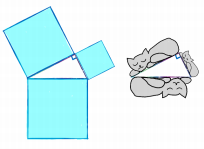
Теперь давайте возьмем равнобедренный прямоугольный треугольник и построим на его сторонах подобные сегменты круга — два синих и один красный, как на рисунке. Здесь уже явно просвечивает луночка Гиппократа.

Сумма площадей синих сегментов равна площади красного сегмента по теореме Пифагора. Отсюда видно, что луночка Гиппократа и равнобедренный прямоугольный треугольник с гипотенузой 2r равновелики (то есть имеют одну и ту же площадь), потому что луночка получается из полукруга вырезанием красного сегмента, а треугольник — вырезанием двух синих сегментов. Поэтому площадь первой луночки Гиппократа равна площади квадрата со стороной r. То, что мы только что проделали, называется квадратурой луночки. В строгом смысле слова квадрировать луночку означает построить равновеликий ей квадрат. Но вполне допускается вместо квадрата использовать другие простые фигуры, например треугольники или четырёхугольники.

Луночки Ибн аль-Хайсама

Если вам понравилось квадрировать луночки и вы хотите сами попробовать, то подумайте над задачей о луночках Ибн аль-Хайсама. Покажите, что сумма площадей жёлтых луночек на рисунке равна площади жёлтого прямоугольного треугольника (окружности построены на сторонах прямоугольного треугольника как на диаметрах). Какой именно прямоугольный треугольник взять, совершенно неважно, поэтому рисунок можно превратить в анимацию (с помощью приложения GeoGebra), подвигав вершину прямого угла. Заметим, что площадь каждой из луночек в отдельности не выражается простой формулой. Тем более интересно, что есть простая формула для их суммарной площади.

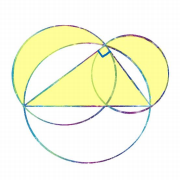
Вторая и четвертая луночки

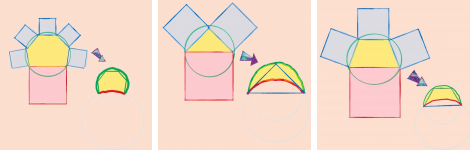
Наша историческая реконструкция мысли Гиппократа не соответствует реальному ходу истории

Третья и пятая луночки

Результаты Вийнквиста переоткрывались несколько раз. В 1840 году это проделал Томас Клаузен, слышавший лишь о первой луночке Гиппократа. Клаузен сумел заинтересовать математическое сообщество новой гипотезой (гипотеза Эйлера — Клаузена) — он предположил, что никаких других квадрируемых луночек циркулем и линейкой построить нельзя.

Клаузен родился в рыбацкой деревне Сногбек в бедной семье, с детства работал, поэтому в школу не ходил и был неграмотным. В двенадцать лет он устроился пастухом к пастору в соседнем приходе. Пастор заметил, что мальчик необыкновенно умен, и разрешил ему совмещать выпас скота с учебой в школе. Кроме того, пастор учил Клаузена астрономии и математике, поскольку сам увлекался этими науками. Блестяще окончив школу, Клаузен по протекции пастора устроился секретарем в обсерваторию в Альтоне, где познакомился с Гауссом, проводившим поблизости от Альтоны геодезические измерения. Гаусс оценил способности молодого человека, что оказалось очень кстати, когда начальник обсерватории уволил Клаузена (они плохо ладили, и последней каплей стал разбитый Клаузеном дорогой барометр). Клаузен отправился в Гёттинген к Гауссу и попросил его замолвить словечко перед шефом. Не в силах отказать Гауссу, начальник обсерватории снова принял Клаузена на работу, но тот, как назло, влюбился в племянницу начальника.

Следующие пятнадцать лет жизни Клаузена могли бы стать сюжетом для одной из самых грустных сказок его соотечественника Ганса Христиана Андерсена. Тем не менее Клаузен продолжал заниматься математикой и астрономией и в 1842 году (когда ему было уже за сорок) получил позицию профессора астрономии в Дерптской обсерватории. Спустя ещё два года Кёнигсбергский университет присудил ему почётную степень — к нему наконец начали относиться в соответствии с его талантами и достижениями. Хотя Клаузен зарабатывал на жизнь астрономией, главным интересом его жизни была чистая математика. Он получил соблазнительное предложение из Пулковской обсерватории, но предпочел остаться в Дерпте (современном Тарту).

Луночки Гиппократа в XX веке и в наши дни

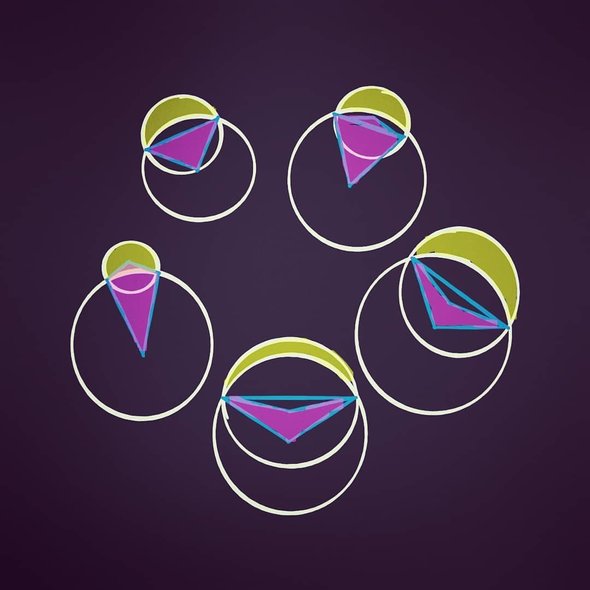
Мы так и не ответили на вопрос, верна или неверна гипотеза Эйлера — Клаузена. Может быть, надо подождать ещё пару тысяч лет и какой-нибудь марсианский математик построит неизвестную науке луночку Гиппократа? Оказывается, что нет, не построит, хотя убедительно объяснить невозможность такого построения совсем не просто.

Двойной удар по гипотезе Эйлера — Клаузена был нанесён в 1934 году с разных сторон: алгебраической (в работе Николая Чеботарёва) и трансцендентной (в работе Александра Гельфонда). Но если Чеботарёв явно решал задачу о луночках, то Гельфонд решил седьмую проблему Гильберта, в которой о луночках не было ни слова. Только в 2003 году Курт Гирстмейр заметил, что результат Гельфонда и его обобщение, полученное Аланом Бейкером (1966), вместе с результатом Чеботарёва, дополненным его учеником Анатолием Дородновым (1947), дают полное доказательство гипотезы Эйлера — Клаузена.

Личности

Доклад о Гиппократе

Биографические сведенья о Гиппократе и его научных достижениях

Гиппократ появился на свет около 460 года до нашей эры на острове Кос в семье потомственного врача – асклепиада. Именно он привил сыну глубокую любовь к медицине и был его первым учителем. Позднее он обучался у знаменитых философов Горгия и Демокрита.

Гиппократ стал первым врачевателем, который отверг распространенную тогда теорию о том, что на человека насылают болезни боги. Благодаря его стараниям медицину выделили в отдельную науку. Он был уверен, что недуги появляются вследствие влияния характера, питания человека, его привычек и природных факторов.

Главное достижение Гиппократа – это выделение человеческих темпераментов. Он считал, что поведение напрямую зависит от уровня черной желчи, крови, слизи и желчи в организме. Также он ввел в медицину термин стадийности.

Считается, что Гиппократ был просто гениальным, выдающимся хирургом Древнего Мира. Он использовал инновационные способы лечения фистул, переломов, ран и вывихов. Кроме того ему принадлежит написание правил, как должен вести себя хирург в ходе оперативного вмешательства. Особый акцент падал на освещение, расположение инструментария и освещение рук. Таким образом, отец медицины впервые сформулировал этические и моральные нормы для врачей. Доктор, согласно его мнению, просто обязан быть трудолюбивым и ответственным, вызывать доверие и хранить врачебную тайну.

Гиппократ умер приблизительно в 370 году до нашей эры.

Интересные факты из жизни Гиппократа

• Он был врачом в истории, который описал раковую опухоль, назвав ее крабом.
• В его честь названо вино – Гипокрас и кратер на обратной стороне Луны.
• Существует легенда, что царь Артаксеркс, владыка империи Ахеменидов, предлагал Гиппократу службу при его дворе. Но древнегреческий врачеватель ответил отказом.
• Был женат. Его женой стала девушка из знатной семьи. Поженились они после того, как Гиппократ закончил домашнее обучение. У супругов было трое детей : мальчики Дракон, Фессал и дочка.
• Однажды он спас Афин от всепоглощающей чумы, почти уничтожившей город.

Надеемся, что доклад про Гиппократа помог Вам к подготовке к занятиям, и Вы узнали много интересного об этом удивительном человеке.

Читайте также:

  

• Культура ульяновской области доклад

  

• Исаак ньютон доклад 5 класс география

  

• Традиции и обычаи хабаровского края доклад

  

• Сильная личность человека сообщение 6 класс доклад инвалиды в самарской области

  

• Права человека и инвалидность доклад комиссии по правам человека оон

1


« Луночки Гиппократа » Выполнила : Учащаяся 8 а класса Шарапова Мария Дмитриевна Научный руководитель : Форсова Ольга Борисовна

2


Актуальность выбранной темы Искусство построения геометрических фигур при помощи циркуля и линейки было в высокой степени развито в Древней Греции, но древним геометрам не удавалось выполнить некоторые построения, используя лишь циркуль и линейку.

3


Цель реферата : Познакомиться с биографией Гиппократа и изучить историю задачи о квадратуре круга и свойства « Луночек Гиппократа »

4


Задачи реферата : 1. Изучить литературу и источники Интернет по данной теме. 2. Ознакомиться с биографией Гиппократа и его открытиями в области медицины, астрономии, геометрии. 3. Изучить задачу о квадратуре круга 4. Изучить свойства « Луночек Гиппократа »

5


Оглавление Кто такой Гиппократ ? Квадратура круга. Луночки Гиппократа. Задача. Вывод. Использованная литература.

6


Кто такой Гиппократ ? Гиппократ Хиосский ( вторая половина V века до н. э.) Древнегреческий геометр, автор первого систематического сочинения по геометрии ( не дошедшего до нас ). Врач и астроном.

7


Квадратура круга Квадратура круга задача, заключающаяся в построении с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу. В 19 веке была строго установлена неразрешимость квадратуры круга с помощью циркуля и линейки. S квадрата = π r 2 сторона равна r π – отношение длины окружности к своему диаметру – число иррациональное. Оно выражается бесконечной непериодической десятичной дробью 3, …

8


Луночки Гиппократа Гиппократовы луночки, три фигуры, указанные Гиппократом Хиосским, каждая из которых ограничена дугами двух окружностей и для каждой из которых с помощью циркуля и линейки можно построить равновеликие прямолинейные фигуры.

9

10


Гиппократ заметил, что суммарная площадь зеленых луночек равна площади квадрата, окрашенного здесь в красный цвет Гиппократ получил четыре квадрируемые луночки.

11


Пусть нижнее основание трапеции является диаметром описанной около нее окружности, АВ = ВС =CD и на боковых сторонах и верхнем основании, как на диаметрах построены полуокружности. Площадь трапеции равна сумме площадей этих луночек и полукруга.

12


Задача Дано : АВСД – квадрат, АВ =4 см, АВ – диаметр круга, 4 малых круга равны. Доказать : равна суммарная площадь зелёных луночек площади квадрата. Доказательство : S АВСД = 4 х 4=16 см ^2, рассмотрим прямоугольный треугольник АСД : АД = СД, угол АДС =90 градусов, по теореме Пифагора ( квадрат гипотенузы равен сумме квадратов катетов ) можно узнать длину отрезка АС : АД = ДС =4 c м => 4^2 х 2= х ^2, х = 32 ~ 5,65 c м. АС диаметр круга ( чёрного )=> R = 5,65/2 = 2,825=> S круга = П R^2 ~25 см ^2 АВ диаметр круга => R = 4/2=2 см => S круга = П R^2 = 2 х 3,14 = 6,28 см ^2 Узнаём суммарную площадь зелёных луночек : Общая S полукругов ~25 c м ^ =9 см ^2( суммарная площадь чёрных полукругов )=> 25-9=16 c м ^2 Суммарная площадь луночек = площади квадрата.

13


Вывод Гиппократ посвятил свою жизнь геометрическим открытиям. На всей ее протяжённости он так и не смог найти решения квадратуре круга, но был близок к нему. Различные другие, продолжавшиеся в течение тысячелетий, попытки найти квадратуру круга оканчивались неудачей. Лишь в 80- х годах 19 в. было строго доказано, что квадратура круга с помощью циркуля и линейки невозможна. Задача о квадратуре круга становится разрешимой, если применять, кроме циркуля и линейки, еще другие средства построения.

14


Использованная литература В. Н. Березин « Луночки Гиппократа » ( журнал Квант 1971, 5) Энциклопедический словарь юного математика / Сост. А. П. Савин. – 3- е изд., испр. и доп. – М.: Педагогика – Пресс, 1997, с.271. Я познаю мир : детская энциклопедия : Математика / Сост. А. П. Савин, В. В. Станцо, А. Ю. Котова : под общ. ред. О. Г. Хинн. – М.: ООО « Издательство АСТ – ЛТД », Гиппократ Хиосский Википедия. Квадратура Круга Википедия.