В
повседневной жизни людям часто приходится находить площадь комнаты, площадь
окна в комнате, площадь садового участка, площадь поля.
Так,
например, площадь комнаты надо знать, чтобы купить необходимое количество
краски для покраски пола в этой комнате. Чтобы найти площадь комнаты, надо её
длину умножить на ширину. Ведь пол комнаты обычно имеет форму прямоугольника.
Таким
же образом можно найти площадь грядки в огороде, так как она представляет собой
прямоугольник.
А
вот как, например, найти площадь лужи? Ведь её границы имеют неправильную форму
– это не прямоугольник, не квадрат и даже не круг.
Сейчас
мы поговорим о том, как найти площадь любой, даже самой искривлённой фигуры.
Посмотрите
на эту прозрачную пластинку или плёнку с разлиновкой в клеточку, которая
называется палеткой. В зависимости от размера фигуры, площадь которой
надо узнать, палетка может быть разделена на квадратные миллиметры, квадратные
сантиметры, квадратные дециметры.
Давайте
найдём площадь вот такой фигуры.
Итак,
возьмём палетку, которая разделена на квадратные сантиметры. Следует
отметить, что в школе чаще всего пользуются именно такими палетками.
Накладываем
эту палетку на нашу фигуру так, чтобы, если это возможно, хотя бы одна сторона
совместилась с линией разлиновки палетки. У нашей фигуры удалось совместить
даже не одну, а две стороны. И уголки верхней и нижней сторон фигуры совпадают
с уголками клеточек палетки.
Сначала
считаем, сколько всего целых квадратов, то есть квадратных сантиметров,
укладывается в данной фигуре. Их 40.
Теперь
считаем все оставшиеся кусочки. Их 12.
Каждые
2 таких кусочка принято засчитывать за 1 полный квадратик. Поэтому количество
таких кусочков надо разделить на 2.
Далее
к 40 прибавляем частное 12 и 2. Получаем 46. Так как
палетка разделена на квадратные сантиметры, то площадь фигуры примерно равна 46
квадратным сантиметрам.
40 + 12 : 2 = 46 (см2)
Примерно,
потому что с помощью палетки площадь фигуры вряд ли можно точно определить.
Ведь 2 кусочка редко могут идеально заменить целый квадратик.
А
сейчас давайте найдём с помощью палетки площадь вот такой фигуры.
Эта
фигура напоминает лужу и здесь уже совместить линии фигуры с разметкой палетки
не получится. Снова воспользуемся палеткой, которая разделена на квадратные
сантиметры. Накладываем её на данную фигуру и считаем целые квадратики. Их 28.
Теперь
считаем кусочки. Их
30.
Снова повторим, что 2 таких кусочка принято
засчитывать за один полный квадратик, поэтому их количество надо разделить на 2.
К
28 прибавим частное 30 и 2. Получим, что площадь рассматриваемой фигуры примерно
равна 43 квадратным сантиметрам.
28 + 30 : 2 = 43 (см2)
Далее
найдём площадь вот такой фигуры.
Накладываем
на неё палетку. В первую очередь считаем, сколько целых квадратиков
укладывается в этой фигуре. Их 26. Теперь
считаем кусочки. Их 21.
Обратите
внимание, что в данном случае количество кусочков – нечётное число. В таком
случае на 2 надо делить ближайшее чётное число, которое больше данного на один,
ведь всё равно с помощью палетки точно найти площадь фигуры невозможно. А вот
почему берём чётное число, которое больше данного, вы узнаете в пятом классе. То
есть надо 22 разделить на 2.
Таким
образом, чтобы найти площадь фигуры, к 26 прибавим частное 22 и 2. Получим, что
площадь примерно равна 37 квадратным сантиметрам.
26 + 22 : 2 = 37 (см2)
И
найдём площадь ещё одной фигуры – треугольника.
Накладываем
на него палетку. Здесь удаётся с разметкой палетки совместить одну из сторон. Я
думаю, вы уже догадались, что если удастся совместить одну из сторон фигуры с
разметкой палетки, и углы фигуры совместятся с уголками квадратиков, то
останется меньше кусочков, и измерение будет более точным.
Сначала
считаем целые квадратики. Их 21. Затем считаем кусочки. Их 18.
Прибавим
к 21 частное 18 и 2 и получим, что площадь треугольника примерно равна 30
квадратным сантиметрам.
21 + 18 : 2 = 30 (см2)
Итак,
повторим, как мы определяем площадь фигуры с помощью палетки.
как определить площадь неправильной фигуры?
Ученик
(128),
закрыт
16 лет назад
Дополнен 16 лет назад
например площадь лужи или разлитой краски.
Дополнен 16 лет назад
ты просто супер!!! Хотя… Никакой не супер..
А просто Гений,гигант мысли!!!
вот так,через задний ход,наплевав на все придуманые формулы,с точностью не уступающей этим же формулам,может только РУССКИЙ человек!!
Мне понравилось!!!
Огромное спасибо:))
Ну ват как не выпить с таким человеком?!!!
Инженер
Высший разум
(199830)
16 лет назад
Пришлось репу почесать, бороденку пощипать. Результаты следующие.
Сфотографируй лужу (перпендикулярно луже) . Сфотографируй шаблон (фигуру с известной площадью, например газету) с того же расстояния.
Загони фотки в комп. Если цифровик – то это просто, если был обычный фотик – распечатай и сканируй.
Возьми программу измерения площади. Их много, например, эту бесплатную
http://www.ssaa.ru/index.php?id=proekt&sn=05.
В ней измеряешь площадь фотографии лужи по сравнению с площадью шаблона.
Если фото уже есть на бумаге, то можно еще так.
Вырезаешь контур лужи на фото (чем больше фото и толще фотобумага, тем будет точнее) . Вырезаешь контур шаблона на фото. Ищешь весы, которые хотя бы точность 0,1 грамма имеют ( например в ломбарде золото вешают такими, или в зоомагазине мотыля отвешивают, или в школьной лаборатории химии есть всегда) . Взвешиваешь вырезанные “лужу” и шаблон. Зная реальную площадь шаблона через соотношение веса вычисляешь реальную площадь лужи.
С краской (высохшей) еще проще. Копируешь контур пятна, лучше на ватман, он тяжелее (точность больше будет) . Вырезаешь пятно и шаблон. Взвешиваешь то и другое. Вычисляешь. Точность весов для ватмана уже а полграмма достаточна будет.
Это методы относительно прямого измерения. Никаких округлений и приближений. Точность ограничена только точностью весов. Да и быстро это по сравнению с разбиением сложной фигуры на простые фигурки с последующим суммированием их площадей.
Как контур лужи на бумагу перенести без фотографирования для последующего вырезания – задавай в вопросах. Надеюсь что-нибудь придумаю.
Skad
Гуру
(4356)
16 лет назад
1) Перефести контур фигуры в цифровой вид, с помощью фотика и проги оцифровки графика.
2) с помощью сплайнирования получить формулу для верхней и нижней границы фигуры. Это удобно сделать в маткаде.
3) посчитать площадь через интеграл.
ИЛИ
Нанести на фигуру сетку с мелким шагом. Посчитать кол-во полностью заполненых ячеек, неполностью заполненые ячейки считаются за 0.5 заполненой.
Татьяна Рылеева
Ученик
(234)
7 лет назад
Пришлось репу почесать, бороденку пощипать. Результаты следующие.
Сфотографируй лужу (перпендикулярно луже) . Сфотографируй шаблон (фигуру с известной площадью, например газету) с того же расстояния.
Загони фотки в комп. Если цифровик – то это просто, если был обычный фотик – распечатай и сканируй.
Возьми программу измерения площади. Их много, например, эту бесплатную
http://www.ssaa.ru/index.php?id=proekt&sn=05.
В ней измеряешь площадь фотографии лужи по сравнению с площадью шаблона.
Если фото уже есть на бумаге, то можно еще так.
Вырезаешь контур лужи на фото (чем больше фото и толще фотобумага, тем будет точнее) . Вырезаешь контур шаблона на фото. Ищешь весы, которые хотя бы точность 0,1 грамма имеют ( например в ломбарде золото вешают такими, или в зоомагазине мотыля отвешивают, или в школьной лаборатории химии есть всегда) . Взвешиваешь вырезанные “лужу” и шаблон. Зная реальную площадь шаблона через соотношение веса вычисляешь реальную площадь лужи.
С краской (высохшей) еще проще. Копируешь контур пятна, лучше на ватман, он тяжелее (точность больше будет) . Вырезаешь пятно и шаблон. Взвешиваешь то и другое. Вычисляешь. Точность весов для ватмана уже а полграмма достаточна будет.
Это методы относительно прямого измерения. Никаких округлений и приближений. Точность ограничена только точностью весов. Да и быстро это по сравнению с разбиением сложной фигуры на простые фигурки с последующим суммированием их площадей.
Как контур лужи на бумагу перенести без фотографирования для последующего вырезания – задавай в вопросах. Надеюсь что-нибудь придумаю.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к исследовательской работе Как измерить лужу
Содержание
-
1.
Презентация к исследовательской работе Как измерить лужу -
2.
Актуальность исследования -
3.
Гипотеза: лужу можно измерить -
4.
2.1. Что такое лужа и ее значение -
5.
Как образуются лужи -
6.
Слайд 6 -
7.
Значение лужи -
8.
Значение лужи -
9.
Слайд 9 -
10.
Лужи на картинах -
11.
Слайд 11 -
12.
Слайд 12 -
13.
Лужи в стихах -
14.
Слайд 14 -
15.
Выводы: 1. Лужа имеет ширину, длину, и -
16.
Исследование 2. Возможные варианты измерения луж различными -
17.
Исследование 3 а). Различные способы измерения периметра -
18.
Исследование 3. б) Измерение периметра лужи «ногами».Цель -
19.
Исследование 4. Нахождение площади лужи с помощью -
20.
Исследование 5. Нахождение площади лужи с помощью -
21.
Слайд 21 -
22.
Спасибо за внимание!
Актуальность исследования Проблема исследования состоит в выяснение вопроса, как и чем можно измерить лужу. Цель исследования заключается в получении способов измерения лужи. Объект исследования: плоские фигуры
Слайд 1Как измерить лужу
Исследовательская работа
Авторы:
ученицы 5 М класса МАОУ «Средняя школа №8»
Илькович Маргарита Евгеньевна Орехова Полина Владимировна
Руководитель: Чернова Ольга Васильевна, учитель математики МАОУ «Средняя школа№8»
г. Когалым 2016 г

Слайд 2 Актуальность исследования
Проблема исследования состоит в
выяснение вопроса, как и чем можно измерить лужу.
Цель исследования заключается в получении способов измерения лужи.
Объект исследования: плоские фигуры неопределенной формы.
Предмет исследования: параметрические характеристики плоских фигур (длина, ширина, периметр, площадь).

Слайд 3 Гипотеза: лужу можно измерить ( исключив ее глубину),
если:
1) поверхность лужи представить как плоскую фигуру;
2) знать ее длину, ширину, периметр;
3) чем больше периметр лужи, тем больше ее площадь.
Задачи:
1.Изучить и проанализировать литературу по образованию и значению луж для человека и живых организмов, рассмотреть лужи в картинах и стихах.
2. Исследовать «суперлужи» нашего города, выяснить причины их возникновения.
3.Рассмотреть возможные способы измерения периметра и площади лужи.
Методы исследования: сбор, изучение, анализ обобщение теоретического и практического материала, измерение лужи различными способами, рефлексивное осмысливание результатов исследования.

Слайд 42.1. Что такое лужа и ее значение

Слайд 13 Лужи в стихах
Н. Щербинина
Лужи, лужи на дорожке!
Обувай скорей сапожки.
Побежим с тобой по лужам.
Мне товарищ очень нужен,
Ведь по лужам под дождем
Лучше бегать нам вдвоем.
Н.Шемякина
Развалилась неуклюже
Посреди дороги лужа.
Я её прошу:
– Простите,
Чуть подвиньтесь, пропустите!
А она в ответ мне:
– Здрасьте!?
Как хотите, перелазьте!

Слайд 14 2.2. Лужа как
математический объект
Исследование 1. « Суперлужи» города Когалыма.
Цель: изучение параметров лужи.

Слайд 15Выводы:
1. Лужа имеет ширину, длину, и глубину. Ширину и длину
я измеряла рулеткой, и глубину, можно измерить с помощью линейки или специальных сапог. Глубина лужи не влияет на ее видимые размеры.
2.Если есть лужа, то причиной ее является, либо весна или осень, либо плачевное состояние наших дорог.
Для ремонта дорог, надо знать какую площадь необходимо засыпать, и для этого нам нужны размеры луж.

Слайд 16Исследование 2. Возможные варианты измерения луж различными измерительными приспособлениями .
Цель: измерить
лужи различными измерительными приспособлениями.
Вывод: периметр лужи можно измерить с помощью различных измерительных приспособлений, снежками, корабликами, палкой, линейкой и т.д. Лужа похожа на многие геометрические фигуры, чаще они бесформенные.

Слайд 17Исследование 3 а). Различные способы измерения периметра одной лужи.
Цель: выбрать наиболее
удобный способ измерения периметра лужи
Вывод: неудобство карандаша на больших лужах, рулетка – не всегда может быть при мне, шаги отличаются друг от друга. Самый удобный способ – ногами ( ноги всегда при мне).

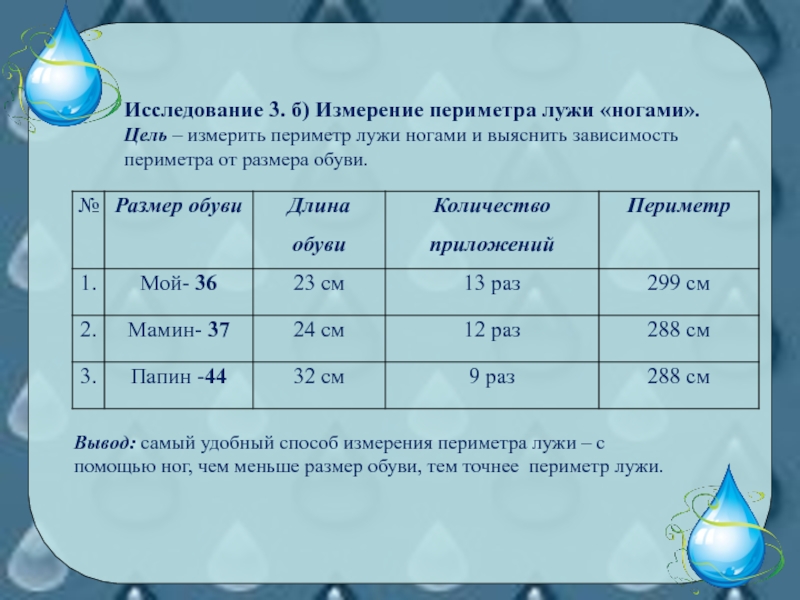
Слайд 18Исследование 3. б) Измерение периметра лужи «ногами».
Цель – измерить периметр лужи
ногами и выяснить зависимость периметра от размера обуви.
Вывод: самый удобный способ измерения периметра лужи – с помощью ног, чем меньше размер обуви, тем точнее периметр лужи.
Слайд 19Исследование 4. Нахождение площади лужи с помощью палетки.
Цель: измерение периметра
и площади кляксы
Вывод: чем больше клякса, тем больше ее периметр и больше ее площадь. Кляксы похожи на круг, овал, треугольник.

Слайд 20Исследование 5. Нахождение площади лужи с помощью сетки.
Цель: измерить площади луж
произвольной формы с помощью сетки
Вывод: найти площадь лужи произвольной формы можно с помощью сетки, клетка которой представляет собой квадрат со стороной 5 см. Этот способ удобен для нахождения площади любой лужи, которую надо засыпать ( например лужу возле гаража).

![]()
Реши задачу
После нескольких дней проливных дождей во дворе образовалась большая круглая лужа радиусом
2
,
5
2,5 м. Найди площадь лужи, если
π
≈
3
π≈3.
В ответ запиши число, округлённое до десятых.
Остались вопросы?
Новые вопросы по предмету Математика
«Измерение площадей плоских фигур произвольной формы: нестандартные методы»
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Шихалиев Р.М. 1
1МБОУ “СОШ №3 г. Тосно”
Неизвестный Е.В. 1
1МБОУ “СОШ №3 г. Тосно”
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
Работа посвящена исследованию и сравнению методов измерения площадей фигур произвольной формы.
Актуальность и практическая значимость исследования.
В школьном курсе математики мы в основном имеем дело с многоугольниками. С проблемой вычисления площади фигур я столкнулся при решении различных задач, суть которых сводилась к тому, что требовалось найти площадь различных многоугольников, которых мы не рассматривали на уроках математики. Ведь до 8 класса мы знакомимся только с формулами для вычисления площади квадрата, прямоугольника и прямоугольного треугольника. Так как на уроке мы обычно выполняем решение в тетради, то я обратил внимание, что вычислить площадь того же квадрата помогают клетки, изображенные в тетради. Просматривая различную информацию в интернете, я натолкнулся на формулу, которая позволяет вычислить площадь фигуры, но только не по клеткам, а по их узлам. Между тем, на практике часто возникает необходимость найти площадь фигуры неправильной формы. Например, необходимость определить площадь территории по плану или карте. Но для площадей сложных фигур отсутствуют общие формулы, аналогичные формулам для многоугольников. Впоследствии мне захотелось узнать, есть ли другие способы для вычисления площади различных фигур на клетчатой бумаге, какой из них проще, менее затратен по времени.
Гипотеза: площадь сложной фигуры может быть измерена приближенными методами с точностью, достаточной для практических целей.
Цель работы: исследовать различные способы вычисления площадей фигур, сравнить полученные результаты.
Задачи исследования:
изучить литературу по исследуемой теме;
отобрать интересную и понятную информацию для исследования;
найти различные методы и приёмы вычисления площади фигур на клетчатой бумаге.
изучение методов нахождения площади с помощью взвешивания.
измерение с помощью методов взвешивания площадей контрольных фигур: прямоугольника, квадрата, выявление погрешностей измерения
провести сравнительный анализ “плюсов” и “минусов” найденных способов.
провести эксперимент в 8В классе об выявлении математических знаний у учащихся при вычислении площади фигур;
Поиск интересных задач на нахождение площади фигуры.
проанализировать и систематизировать полученную информацию.
Объектом исследования являются методы измерения площади фигур произвольной формы:
1) метод взвешивания;
2) использование клетчатой бумаги;
3) применение точных формул.
Предметом исследования является площадь фигур произвольной формы.
Из истории возникновения понятия “Площадь”.
В повседневной жизни мы часто встречаемся с понятием площади. Мы говорим: площадь квартиры, площадь садового участка и т.д.
Необходимость в понятии «площадь» возникла из жизненных потребностей. В древности люди использовали для измерения длин те измерительные приборы, которые всегда были при себе.
Позже возникла потребность в измерении и сравнении разнообразных «фигур» (н.п. земельных участков). Было необходимо ввести величину, которая характеризовала бы величину той части плоскости, которую занимает фигура. Эту величину назвали площадью.
Измерение площадей является одним из самых древних разделов геометрии. В частности, название “геометрия” означает “землемерие”, т.е. связано именно с измерением площадей. Основы этой науки были заложены в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, т. е. вычислять их площади.
Вавилоняне, так же как и египтяне измеряли большей частью простейшие фигуры, встречающиеся при межевании земель, возведении стен и насыпей, строительстве плотин и каналов и т.п.
Сохранилось немало планов земельных угодий, разделенных на прямоугольники, трапеции и треугольники, а также планов различных строений, свидетельствующих, что вавилонский землемер или архитектор должен был хорошо чертить и проводить геометрические расчеты.
Многие ученые решали проблему вычисления площади фигуры. В историю с понятием площади вошли имена Евклида, Архимеда, Пифагора, Герона Александрийского, Рене Декарта, Пьера Ферма, Георга Пика и др. Ими открыто большое количество различных формул и способов для вычисления площади фигуры.
Способы вычисления площади фигуры на клетчатой бумаге.
При изучении вычисления площадей многоугольников на клетчатой бумаге я заметил, что все задачи строятся на понятии узла. Узел напоминает узел в рыболовной сетке – пересечение горизонтальных и вертикальных линий. Все задачи достаточно разнообразны и занимательны, они заставляют думать, размышлять, анализировать, искать аналогии.
Рис.1. фотография рыбацкой сетки
Рассмотрим вычисление площади одной и той же фигуры тремя способами и сравним результат вычисления. [1, с.36]
Три способа вычисления площади выпуклого многоугольника.
Разбиение. Смысл данного способа состоит в том, что многоугольник разрезается на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
Тогда площадь фигуры можно сосчитать по формуле:
Sф = S1 + S2 + S3 = 10 + 1 + 12 = 23.
Дополнение до прямоугольника. Смысл данного способа – это дополнение многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Получим, что площадь фигуры равна:
Sф = Sпр – (S1 + S2) = 36 – (1 + 12) = 23.
Формула Пика. Любая фигура изображенная на листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника. Нас интересуют внутренние узлы и узлы, которые лежат на границе многоугольника. Тогда формула выглядит так S = В + Г/2 – 1, где В – количество внутренних узлов, а Г – количество узлов на границе многоугольника.
Эта формула получила название формула Пика в честь австрийского математика Георга Пика которая появилась в его восьмистраничной работе 1899 года, опубликованной в Праге.
Используя рисунок В= 17, Г = 14, получаем
S = 17 + 14/2 – 1 = 23.
Вычисляя площадь выпуклого многоугольника тремя способами, я получил один и тот же результат.
Три способа вычисления площади невыпуклого многоугольника.
Способ разбиенияне подходит для данной фигуры, т.к. невозможно разбить ее на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
Дополнение до прямоугольника.
Достраивая многоугольник до прямоугольника, и отсекая лишние части, найдем площадь фигуры
Sф = S – (S1 + S2 + S3 + S4) = 42 – (6 + 2 + 1 + 1) = 16 – 10 = 6.
ФормулаПика.
При подсчете внутренних узлов многоугольника и узлов, лежащих на границе получим, что
В = 5; Г = 4; S = 5 + 4/2 – 1 = 6.
И опять я получил один и тот же результат.
Вычисление площади кольца по формуле Пика.
А если взять не многоугольник, а, например, кольцо и перенести его на клетчатую бумагу? Понятно, что первый и второй способы не удастся использовать. Применим формулу Пика и сравним полученный результат с результатом, полученным используя формулу для вычисления площади круга.
Возьмем кольцо, которое построим с помощью двух окружностей с радиусами R=4 и r = 2.
Вычислим площадь кольца с помощью формулы Пика:
В = 32, Г = 8, S= 32 + 4 – 1 = 35.
Вычислим площадь кольца по формуле площади круга, округлив число π до единиц.
S = πR2 – πr2 = 3* 16 – 3*4 = 48 – 12 = 36.
Округлим теперь π до десятых:
S = πR2 – πr2 = 3,1* 16 – 3,1*4 = 49,6 – 12,4 = 37,2.
А если округлить число π до сотых, то получим:
S = πR2 – πr2 = 3,14* 16 – 3,14*4 = 50, 24 – 12,56 = 37,68.
Сравнив результаты можно сделать вывод, что существует погрешность в вычислении площади по формуле Пика и чем точнее число π, тем она больше. Следовательно, данную формулу можно применять только для вычисления площадей многоугольников. [2, с.17], [4]
Метод взвешивания
Метод измерения вспомогательной величины придуман еще в древности и заключается в измерении массы плоской копии измеряемой фигуры. Если толщина листа, из которого изготовлены взвешиваемая фигура, постоянна, то масса фигуры прямо пропорциональна ее площади. Нужно нанести на плотную бумагу квадрат, площадь которого S0 точно известна, вырезать его и определить на весах его массу m0. На такую же бумагу перенести фигуру с искомой площадью S. Вырезать фигуру и определите её массу m. Затем, пользуясь правилом пропорции – S/S0 = m/m0, вычислить искомую площадь. [3, с.65]
Тогда
Вычисление площади клинового листа
Для решения задачи была взят фотография кленового листа (рис. 2).
Рисунок 2. Фотография листа клена
1Разбиение.
Окантовка листа была перенесена на лист бумаги и была разбита (разрезана) на прямоугольники и (или) прямоугольные треугольники. (Рисунок 3).
Рисунок 3. Разбиение листа клена на прямоугольники и прямоугольные треугольники
После чего произведен расчет площади каждого прямоугольника и прямоугольного треугольника в см2
|
7,56 |
||
Тогда общая площадь листа будет равна:
Sобщая = S1+S2+…+S54
см2
2. Дополнение до прямоугольника.
Окантовка листа была перенесена на лист бумаги и была дополнена до прямоугольника. (Рисунок 4).
Рисунок 4. Дополнение листа клена на прямоугольника
После чего произведен расчет площади общего прямоугольника и каждого прямоугольника и прямоугольного треугольника в см2
Общий прямоугольник имеет размеры 18,2 см на 15 см, т. Е. его площадь прямоугольника составляет S=18,2∙15=273 см2
Sобщая= S – (S1+S2+…+S42)
см2
3Формула Пика.
Окантовка листа была перенесена на миллиметровую бумагу. (Рисунок 5).
Рисунок 5. Разбиение листа клена на узлы
В (внутренние точки) =13353 шт.
Г (граничные точки) = 725 шт.
Тогда по формуле S = В + Г/2 – 1
S=13353+362,5-1=13714,5мм2=137,145 см2
4. Метод взвешивания
Для проведения взвешивания взяли лист бумаги SvetoCopy. По ее плотности определили вес бумаги при помощи таблицы и путем взвешивания. Результаты сошлись. Вес одного листа бумаги А4 =5г. Размеры листа А4 равны 210х297мм, т.е. площадь одного листа равна S0 = 623,7 см2
Рис. 6. Фотография оборотной стороны упаковки бумаги SvetoCopy
Рис. 7. Таблицы дляболее точного измерения массы листа по его плотности.
Для определения погрешности вычислений вырезали в качестве эталонов несколько геометрических фигур (прямоугольник (эталон 1) и квадрат (эталон 2)), площадь которых можно сравнить вычислив ее по формуле.
Прямоугольник имеет размеры: 7см на 5 см, а квадрат: 5см на 5см.
S0 = 623,7 см2
т0= 5000мг
|
Наименование образца |
Площадь по формуле, см2 |
Взвешивание |
Погрешность измерения ∆ |
|
|
Масса, мг |
Площадь, см2 |
|||
|
эталон 1 |
35 |
250 |
31,185 |
1,908 |
|
эталон 2 |
25 |
150 |
18,711 |
3,145 |
|
Лист А4 |
623,7 |
5000 |
623,7 |
0 |
|
Лист клена |
– |
1100 |
137,214 |
2,526 |
Количественной характеристикой точности является погрешность измерения. Если известно точное значение некоторой величины и ее приближенное значение x, то предельной абсолютной погрешностью приближенного значения называется величина , а предельной относительной погрешностью – величина . Однако на практике точные значения измеряемой величины неизвестны, а приближенное значение заключено в некоторых пределах: . В этом случае считают, что .
Таким образом после взвешивания величина площади листа клена составляет 137,214 см2 с погрешностью измерения 2,53 см2
Рис. 8. Фотографии опреденения массы листа
Сравнительный анализ способов нахождения площади многоугольника на клетчатой бумаге.
1. Разбиение.
Этот способ прост в подсчёте площадей фигур, которые разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки. К ним относятся выпуклые многоугольники.
К минусам можно отнести то, что в использовании этого способа приходится производить множество действий, а так же невозможность подсчёта площади фигур, которые не разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
2. Дополнение до прямоугольника.
Этот способ так же прост в подсчёте при вычислении площади при небольшом количестве фигур, площадь которых необходимо отнять.
Минусы этого способа – сложность подсчёта площади многоугольников необычной
формы, большое количество фигур, площадь которых необходимо отнять, а так же невозможность подсчёта площади фигур, не относящихся к многоугольникам.
3. Формула Пика.
К плюсам я отнес то, что легко вычисляется площадь многоугольника с необычной формой, в отличие от предыдущих способов, краткость формулы, а так же возможность вычисления приближенного значения площади местности по карте, представив ее в виде многоугольника, перенеся ее на клетку.
Минусами этого способа считаю сложность вычисления площади фигуры с большим количеством узлов, а так же, если в фигуре есть «спорные» узлы (узлы, лежащие близко к стороне многоугольника). Вычисляя площадь фигур, не относящихся к многоугольникам, результат получается не точным.
4. Метод взвешивания.
К минусам я отнес, что можно вычислить площадь фигуры с помощью весов с большой погрешностью измерения и большей продолжительности времени измерения
Заключение
Изучив различные источники, выяснилось, что существует различные способы вычисления фигур по клеткам, но для меня были интересны и понятны три: разбиение, дополнение до прямоугольника и вычисления по формуле Пика.
Моя гипотеза – о том, что если геометрическая фигура изображена на клетчатой бумаге, то ее площадь можно вычислить различными способами и убедиться, что результаты вычислений будут одинаковыми, частично подтвердилась. Рассмотрев все три способа, я пришел к выводу, что не для всякой фигуры можно приметить каждый из них. У каждого из них есть свои плюсы и минусы.
Все три способа можно применить только для выпуклых многоугольников, перенеся их на клетчатую поверхность.
Формула Пика интересна своей простотой. И пусть она при вычислении площадей, не относящихся к многоугольникам, дает приближенное значение, можно легко оценить площадь той или иной территории на карте.
Как показал метод взвешивания является пригодным для приближенного нахождения площадей фигур сложной формы.
Список литературы и Интернет-ресурсов
Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
История математики с древнейших времен до начала XIX столетия, под редакцией Ю.П. Юшкевича., издательство Наука., М., 1970г
Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.
https://ege.sdamgia.ru/
http://www.pppa.ru/additional/01geodesy/06/02topo.php
http://ru.wikihow.comhttp://knowledge.allbest.ru/mathematics/3c0b65635b3bd68b4c43b89521306d27_0.html
http://argonavt.narod.ru/Kenpark.html
Приложение 1
Опрос сверстников о знании ими способов вычисления площадей плоских фигур
Анкета
Умеете ли вы определять площадь не стандартного многоугольника?
Если да, то как? (определите площади следующих фигур)
А можете ли вы определить площадь нестандартной фигуры (например, площадь лужи). И если да, то как?
Результаты опроса
1 вопрос:
Рис. 9. Гистограмма ответов на 1 вопрос
2. вопрос:
Рис. 10. Гистограмма ответов на 2 вопрос
Вывод по 1 и 2 вопросу: практически 70% респондентов не владеют знаниями вычисления площади многоугольника, если он не стандартной формы.
3 вопрос:
Рис. 11. Гистограмма ответов на 3 вопрос
После проведения анкетирования я показал как измерить площадь лужи при помощи палетки (использовал видео с сайта «математические этюды»)
Рис. 12. Фотографии моего рассказа одноклассникам о измерении площади лужи при помощи палетки
Приложение 2
Работы одноклассников по вычислению площади собственной ладони по формуле Пика
Рис. 13. Фотографии работ одноклассников по вычислению площади собственной ладони по формуле Пика
Просмотров работы: 5093
