Р
ассмотрим
регулярную поверхность
,
заданную уравнением
,
где
.
Разобьём данную поверхность на элементы
,
где
.
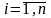
Обозначим
– диаметр наименьшего шара, в который
можно вписать участок
.
Обозначим
и назовём его диаметром разбиения.
Выберем на каждом участке точку
и проведём через эту точку касательную
плоскость к поверхности
.
Обозначим эти плоскости
.
Ортогональную проекцию участка
на плоскость
обозначим
.
Ортогональная проекция – это плоская
фигура. Её площадь обозначим
и
составим сумму:
,
(1)
где
– полная площадь поверхности
.
Площадью
назовём предел суммы (1) при
,
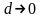
причём этот предел не должен зависеть
ни от способа разбиения поверхности на
участки, ни от выбора точек
.
Теорема: Площадь регулярной
поверхности, заданной уравнением
,
где
может быть вычислена по формуле:
.
где для регулярной поверхности всегда
выполняется равенство
.
Доказательство.
Разобьём поверхность на участки
,
и на каждом участке выберем точки
.
Так как поверхность регулярная, то через
можно провести касательную плоскость
и выбрать систему координат таким
образом, чтобы оси OX и OY
лежали в касательной плоскости, точка
O совпадала с
,
а ось
была перпендикулярна плоскости. Тогда
в данной локальной системе координат
уравнение участка поверхности
можно записать в параметрическом виде:
.
А теперь спроектируем
на касательную плоскость. Получим фигуру
,
её уравнения в данной системе координат
имеют следующий вид:
,
где
.
Площадь этой фигуры:
.
Переходя к координатам
,
имеем:
,
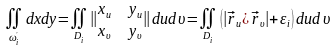
где
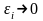
при
.
Окончательно получаем:
,
где
– площадь поверхности
.
Следовательно, вся площадь
равна:
.
Переходя к пределу, когда
получим:
.
Так как
(так как
при
)
, то последний предел идёт в ноль.
Следовательно, площадь поверхности
равна:
,
что и требовалось доказать.
В §10 мы записали, что
.
Очевидно, что
.
Исходя из этого, получаем:
.
Если поверхность задана в виде
,
где
,
тогда (§10)
,
,
.
Следовательно, имеем:
.
Функцию
можно
представить в векторном виде следующим
образом:
.
Вектор нормали к поверхности имеем вид
.
Запишем направляющие косинусы этого
вектора:
,
,
.
Следовательно:
,
где
– угол между нормальным вектором и осью
.
Отсюда следует, что если поверхность
задана уравнением
,
где
,
то её площадь можно найти по формуле:
.
§10. Поверхностный интеграл первого рода: определение, физический смысл, теорема о среднем.
Рассмотрим
регулярную поверхность
.
Вектор
представим в следующем виде:
.
Пусть E,F,G
– коэффициенты первой квадратичной
формы данной поверхности, и пусть в
каждой точке поверхности определена
непрерывная функция
.
Обозначим данную поверхность .
Поверхностным интегралом первого
рода называют:
.
(1)
Физический смысл поверхностного
интеграла первого рода.
Пусть на поверхности
распределена масса, плотность которой
является функцией
.
Тогда сумма
приближённо равна массе этой поверхности,
а переходя к пределу получим массу
поверхности, то есть:
.
С помощью поверхностного интеграла
первого рода можно находить координаты
центра масс, момент инерции материальных
поверхностей с плотностью
.
Координаты центра масс:
,
,
.
Момент инерции:
,
,
.
Свойства поверхностного интеграла
первого рода следуют согласно определению
(1) из свойств двойного интеграла. А
также: если поверхность состоит из
нескольких поверхностей
,
(причём
)
то в этом случае:
.
Теорема
о среднем: пусть существует поверхностный
интеграл первого рода ,тогда:
Существует
k
[inf(f)
, sup(f)] такой
что :
k*S;
Интегральное
среднее: k=
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Площадь поверхности
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Первая квадратичная форма поверхности.
Начать изучение
-
Площадь простой поверхности.
Начать изучение
-
Площадь почти простой поверхности.
Начать изучение
Первая квадратичная форма поверхности.
Пусть простая поверхность задана векторным уравнением
$$
boldsymbol{r} = boldsymbol{r}(u, v), (u, v) in overline{Omega},label{ref1}
$$
где (Omega) плоская область.
Найдем скалярный квадрат вектора
$$
dboldsymbol{r} = boldsymbol{r}_{u}(u, v) du + boldsymbol{r}_{v}(u, v) dv.nonumber
$$
Полагая
$$
E = (boldsymbol{r}_{u}, boldsymbol{r}_{u}),quad F = (boldsymbol{r}_{u}, boldsymbol{r}_{v}),quad G = (boldsymbol{r}_{v}, boldsymbol{r}_{v}),label{ref2}
$$
получаем, что справедлива формула
$$
|dboldsymbol{r}|^{2} = (dboldsymbol{r}, dboldsymbol{r}) = E(u, v) du^{2} + 2F(u, v) du dv + G(u, v) dv^{2}.label{ref3}
$$
Выражение, стоящее в правой части равенства eqref{ref3}, называется первой квадратичной формой поверхности, числа (E), (F) и (G) называются коэффициентами первой квадратичной формы поверхности.
Лемма 1.
Первая квадратичная форма простой поверхности положительно определена, то есть (|dboldsymbol{r}|^{2} > 0), если ((du)^{2} + (dv)^{2} > 0).
Доказательство.
(circ) Так как
$$
(boldsymbol{a}, boldsymbol{b}) = |boldsymbol{a}| cdot |boldsymbol{b}| cos widehat{boldsymbol{ab}},quad |[boldsymbol{a}, boldsymbol{b}]| = |boldsymbol{a}| cdot |boldsymbol{b}| cdot |sin widehat{boldsymbol{ab}}|,nonumber
$$
то справедливо тождество
$$
|[boldsymbol{a}, boldsymbol{b}]|^{2} = |boldsymbol{a}|^{2} cdot |boldsymbol{b}|^{2}-|(boldsymbol{a}, boldsymbol{b})|^{2},nonumber
$$
Подставляя в это тождество (boldsymbol{a} = boldsymbol{r}_{u}), (boldsymbol{b} = boldsymbol{r}_{v}), и пользуясь тем, что в любой точке простой поверхности векторы (boldsymbol{r}_{u}) и (boldsymbol{r}_{v}) неколлинеарны, получаем
$$
|[boldsymbol{r}_{u}, boldsymbol{r}_{v}]|^{2} = EG-F^{2} > 0.nonumber
$$
Условия (E > 0), (G > 0), (EG-F^{2} > 0) достаточны для положительной определенности первой квадратичной формы поверхности. (bullet)
Говорят, что первая квадратичная форма задает на поверхности метрику. Зная коэффициенты первой квадратичной формы поверхности, можно вычислить длины кривых, лежащих на поверхности, определить площадь поверхности. Например, дифференциалы длин дуг координатных кривых, проходящих через точку (A(u, v)) поверхности, равны следующим величинам:
$$
ds_{1} = |boldsymbol{r}_{u}du| = sqrt{E}|du|,quad ds_{2} = |boldsymbol{r}_{v}dv| = sqrt{G}|dv|.label{ref4}
$$
Площадь простой поверхности.
Пусть простая поверхность задана уравнением eqref{ref1}. Рассмотрим на поверхности криволинейный параллелограмм, ограниченный координатными линиями (u), (u + Delta u), (v), (v + Delta v). Векторы (boldsymbol{r}_{u}(u, v)Delta u) и (boldsymbol{r}_{v}(u, v)Delta v) будут касательными к координатным линиям, проходящим через точку (A(u, v)) поверхности (рис. 53.1), а длины этих векторов в силу формул eqref{ref4} будут отличаться от длин сторон криволинейного параллелограмма на (o(Delta u)) и (o(Delta v)) соответственно при (Delta u rightarrow 0), (Delta v rightarrow 0). Поэтому естественно считать, что площадь криволинейного параллелограмма приближенно равна площади (dS) параллелограмма, построенного на векторах (boldsymbol{r}_{u} Delta u) и (boldsymbol{r}_{v} Delta v). Таким образом, при (Delta u > 0), (Delta v > 0).
$$
dS = |[boldsymbol{r}_{u}, boldsymbol{r}_{v}] Delta u Delta v| = sqrt{EG-F^{2}} du dv.label{ref5}
$$
Выражение eqref{ref5} называется элементом площади поверхности.
Определим формально площадь простой поверхности (Sigma) как следующий двойной интеграл (область (Omega) предполагается измеримой по Жордану):
$$
S(Sigma) = iintlimits_{Omega} |[boldsymbol{r}_{u}, boldsymbol{r}_{v}]| du dv = iintlimits_{Omega} sqrt{EG-F^{2}} du dv.label{ref6}
$$
Это определение оправдано приведенными выше эвристическими рассуждениями, а также перечисленными ниже свойствами площади поверхности.
Свойство 1.
Число (S(Sigma)) не зависит от способа параметризации поверхности.
Доказательство.
(circ) Пусть переход от параметрического уравнения eqref{ref1} к параметрическому уравнению
$$
boldsymbol{rho} = boldsymbol{rho}(u’, v’), (u’, v’) in Omega’,nonumber
$$
совершается при помощи взаимно однозначного и непрерывно дифференцируемого отображения области (Omega’) на область (Omega) с якобианом, не равным нулю. Тогда, воспользовавшись формулой отсюда и формулой замены переменных в двойном интеграле, получаем
$$
S(Sigma) = iintlimits_{Omega’} |[boldsymbol{rho}_{u’}, boldsymbol{rho}_{v’}]| du’ dv’ = iintlimits_{Omega’} |[boldsymbol{r}_{u}, boldsymbol{r}_{v}]| cdot left|frac{partial(u, v)}{partial(u’, v’)}right| du’ dv’ = iintlimits_{Omega} |[boldsymbol{r}_{u}, boldsymbol{r}_{v}]| du dv. bulletnonumber
$$
Свойство 2.
Если поверхность (Sigma) есть плоская измеримая по Жордану область (Omega), заданная уравнениями
$$
x = u, y = v, z = 0, (u, v) in Omega,nonumber
$$
то ее площадь, вычисленная при помощи формулы eqref{ref6}, совпадает с плоской мерой Жордана области (Omega).
Доказательство.
(circ) Так как
$$
boldsymbol{r} = (u, v, 0), boldsymbol{r}_{u} = (1, 0, 0), boldsymbol{r}_{v} = (0, 1, 0), E = G = 1,nonumber F = 0,
$$
то
$$
S(Sigma) = iintlimits_{Omega} |[boldsymbol{r}_{u}, boldsymbol{r}_{v}]| du dv = iintlimits_{Omega} du dv = m(Omega). bulletnonumber
$$
Свойство 3.
Выражение (S(Sigma)) аддитивно зависит от поверхности.
Доказательство.
(circ) Если область (Omega) гладкой перегородкой разбита на области (Omega_{1}) и (Omega_{2}), то и поверхность (Sigma) разобьется на простые поверхности (Sigma_{1}) и (Sigma_{2}). Из аддитивности двойного интеграла по области интегрирования следует, что
$$
S(Sigma) = S(Sigma_{1}) + S(Sigma_{2}). bulletnonumber
$$
Свойство 4.
Для поверхности, являющейся графиком непрерывно дифференцируемой функции на замыкании измеримой по Жордану области (Omega), формула eqref{ref6} для площади поверхности имеет следующий вид:
$$
S(Sigma) = iintlimits_{Omega} sqrt{1 + f_{x}^{2} + f_{y}^{2}} dx dy.label{ref7}
$$
Доказательство.
(circ) Действительно, так как
$$
boldsymbol{r} = (x, y, f(x, y)), boldsymbol{r}_{x} = (1, 0, f_{x}(x, y)), boldsymbol{r}_{y} = (0, 1, f_{y}(x, y)),nonumber
$$
то
$$
E = boldsymbol{r}_{x}^{2} = 1 + f_{x}^{2}, F = (boldsymbol{r}_{x}, boldsymbol{r}_{y}) = f_{x}f_{y}, G = boldsymbol{r}_{y}^{2} = 1 + f_{y}^{2},nonumber
$$
$$
EG-F^{2} = (1 + f_{x}^{2})(1 + f_{y}^{2})-f_{x}^{2}f_{y}^{2} = 1 + f_{x}^{2} + f_{y}^{2}. bulletnonumber
$$
Пример 1.
Найти площадь части сферы (x^{2} + y^{2} + z^{2} = a^{2}), вырезаемой из нее цилиндром (x^{2}-ax + y^{2} = 0) (см. рис. 48.10).
Решение.
(triangle) В силу симметрии достаточно ограничиться рассмотрением той части сферы, которая лежит в первом октанте. Цилиндр будет вырезать из нее множество точек, определяемое следующими неравенствами и равенствами:
$$
x^{2} + y^{2} + z^{2} = a^{2}, x^{2}-ax + y^{2} leq 0, x geq 0, y geq 0, z geq 0.label{ref8}
$$
Если перейти к сферическим координатам, полагая
$$
x = a cos psi cos varphi, y = a cos psi sin varphi, z =a sin psi,label{ref9}
$$
то система равенств и неравенств eqref{ref8} эквивалентна равенствам eqref{ref9} и неравенствам
$$
0 leq varphi leq psi leq frac{pi}{2},label{ref10}
$$
определяющим в плоскости параметров (varphi, psi) треугольную область (Omega) (рис. 53.2). Интересующая нас простая поверхность есть образ треугольной области (Omega) при отображении eqref{ref9}.
Вычислим коэффициенты первой квадратичной формы. Получаем
$$
boldsymbol{r} = (a cos psi cos varphi, a cos psi sin varphi, a sin psi),nonumber
$$
$$
boldsymbol{r}_{psi} = (-a sin psi cos varphi, -a sin psi sin varphi, a cos psi),nonumber
$$
$$
boldsymbol{r}_{varphi} = (-a cos psi sin varphi, a cos psi cos varphi, 0),nonumber
$$
$$
E = boldsymbol{r}_{psi}^{2} = a^{2}, F = (boldsymbol{r}_{varphi}, boldsymbol{r}_{psi}) = 0, G = boldsymbol{r}_{varphi}^{2} = a^{2} cos^{2} psi.nonumber
$$
Площадь части сферы (x^{2} + y^{2} + z^{2} = a^{2}), вырезаемой из нее цилиндром (x^{2}-ax + y^{2} = 0), равна
$$
S(Sigma) = 4 iintlimits_{Omega} sqrt{EG-F^{2}} dvarphi dpsi = 4 intlimits_{0}^{pi/2} dvarphi intlimits_{varphi}^{pi/2} a^{2} cos psi dpsi = 4a^{2} left(frac{pi}{2}-1right). blacktrianglenonumber
$$
Площадь почти простой поверхности.
Почти простая поверхность задается уравнением (boldsymbol{r} = boldsymbol{r}(u, v)), ((u, v) in overline{Omega}), где (Omega) — плоская область. По определению найдется последовательность ограниченных областей ({Omega_{n}}) такая, что (overline{Omega}_{n} subset Omega_{n + 1}), (displaystyleOmega = bigcup_{n=1}^{infty}Omega_{n}) а поверхности (Sigma_{n}), определяемые уравнениями (boldsymbol{r} = boldsymbol{r}(u, v)), ((u, v) in overline{Omega}), являются простыми. Предположим дополнительно, что области (Omega_{n}) измеримы по Жордану. Тогда под площадью (S(Sigma)) почти простой поверхности будем понимать (displaystylelim_{n rightarrow infty} S(Sigma_{n})).
Так как числовая последовательность (S(Sigma_{n})) монотонно возрастает, то она всегда имеет конечный или бесконечный предел
$$
S(Sigma) = lim_{n rightarrow infty} S(Sigma_{n}) = lim_{n rightarrow infty} iintlimits_{Omega_{n}} sqrt{EG-F^{2}} du dv = iintlimits_{Omega} sqrt{EG-F^{2}} du dv.label{ref11}
$$
Интеграл в формуле eqref{ref11} нужно понимать как несобственный. Если область (Omega) измерима по Жордану, а функция (sqrt{EG-F^{2}}) ограничена на (Omega), то интеграл в формуле eqref{ref11} будет двойным интегралом Римана.
Пример 2.
Найти площадь части боковой поверхности конуса (z^{2} = x^{2} + y^{2}), (z geq 0), вырезаемой из нее цилиндром (x^{2}-ax + y^{2} = 0).
Решение.
(triangle) Обозначим часть боковой поверхности конуса, вырезаемую из нее цилиндром, через (Sigma). Если перейти к цилиндрическим координатам, то (Sigma) будет почти простой поверхностью, определяемой параметрическими уравнениями
$$
x = r cos varphi, y = r sin varphi, z = r, (r, varphi) in Omega,nonumber
$$
$$
Omega = left{(r, varphi): r leq a cos varphi, -frac{pi}{2} leq varphi leq frac{pi}{2}right}.nonumber
$$
Найдем коэффициенты первой квадратичной формы этой поверхности:
$$
boldsymbol{r} = (r cos varphi, r sin varphi, r), boldsymbol{r}_{varphi} = (-r sin varphi, r cos varphi, 0),nonumber
$$
$$
boldsymbol{r}_{r} = (cos varphi, sin varphi, 1), E = boldsymbol{r}_{varphi}^{2} = r^{2}, F = 0, G = boldsymbol{r}_{r}^{2} = 2,nonumber
$$
$$
sqrt{EG-F^{2}} dr dvarphi = rsqrt{2} dr dvarphi.nonumber
$$
Применяя формулу eqref{ref11}, получаем
$$
S(Sigma) = iintlimits_{Omega} sqrt{2}r dr dvarphi = sqrt{2} intlimits_{-pi/2}^{pi/2} dvarphi intlimits_{0}^{a cos varphi} r dr = frac{pi a^{2} sqrt{2}}{4}. blacktrianglenonumber
$$
Если поверхность (Sigma) не является простой или почти простой, но может быть разрезана на конечное число простых кусков, то ее площадью называют сумму площадей всех простых кусков.
Алгебра и начала математического анализа, 11 класс
Урок №24. Вычисление площадей с помощью интегралов.
Перечень вопросов, рассматриваемых в теме
1) Нахождение площади фигуры, ограниченной графиками функций с помощью определенного интеграла.
2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница
3) Решение задач, с помощью формулы Ньютона – Лейбница
Формула Ньютона – Лейбница
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием этой криволинейной трапеции
формула Ньютона – Лейбница
Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым. ( зависит от расположения криволинейной трапеции)
Примеры и разбор решения заданий тренировочного модуля
№1 Вычислите площадь фигуры, ограниченной линиями y= x, y = 5 – x, x = 1, x = 2, используя определенный интеграл.
Решение. Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b).
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) – F(а) , это и будет ответ
№2. Найти площадь фигуры, ограниченной линиями у=4-х2,у=3х, у=0 и находящейся в 1-й четверти.
Решение: Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) – F(а) , это и будет ответ.
Решение. S=SOAB +SABC
№3. Найти площадь криволинейной трапеции (х-1)2, ограниченной линиями х=2 и х=1, осью 0х
Решение:
Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) – F(а), это и будет ответ.
В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:
S(G)=∫abf(x)dx для непрерывной и неотрицательной функции y=f(x) на отрезке [a;b],
S(G)=-∫abf(x)dx для непрерывной и неположительной функции y=f(x) на отрезке [a;b].
Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y=f(x) или x=g(y).
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Пусть функции y=f1(x) и y=f2(x) определены и непрерывны на отрезке [a;b], причем f1(x)≤f2(x) для любого значения x из [a;b]. Тогда формула для вычисления площади фигуры G, ограниченной линиями x=a, x=b, y=f1(x) и y=f2(x) будет иметь вид S(G)=∫abf2(x)-f1(x)dx.
Похожая формула будет применима для площади фигуры, ограниченной линиями y=c, y=d, x=g1(y) и x=g2(y): S(G)=∫cd(g2(y)-g1(y)dy.
Разберем три случая, для которых формула будет справедлива.
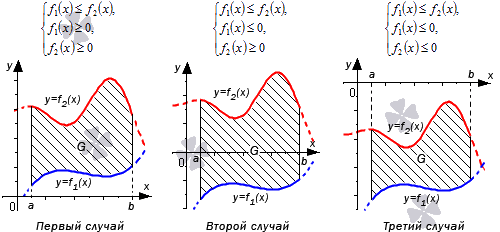
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G1 равна площади фигуры G2. Это значит, что
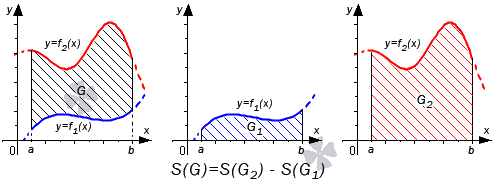
Поэтому, S(G)=S(G2)-S(G1)=∫abf2(x)dx-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx.
Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.
Во втором случае справедливо равенство: S(G)=S(G2)+S(G1)=∫abf2(x)dx+-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx
Графическая иллюстрация будет иметь вид:
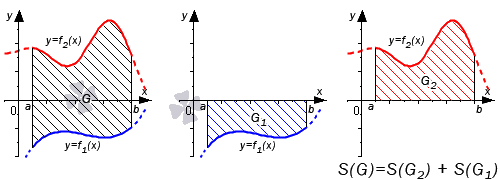
Если обе функции неположительные, получаем: S(G)=S(G2)-S(G1)=-∫abf2(x)dx–∫abf1(x)dx=∫ab(f2(x)-f1(x))dx . Графическая иллюстрация будет иметь вид:
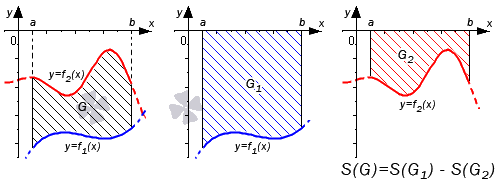
Перейдем к рассмотрению общего случая, когда y=f1(x) и y=f2(x) пересекают ось Ox.
Точки пересечения мы обозначим как xi, i=1, 2,…, n-1. Эти точки разбивают отрезок [a; b] на n частей xi-1; xi, i=1, 2,…, n, где α=x0<x1<x2<…<xn-1<xn=b. Фигуру G можно представить объединением фигур Gi, i=1, 2,…, n. Очевидно, что на своем интервале Gi попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S(Gi)=∫xi-1xi(f2(x)-f1(x))dx, i=1, 2,…, n
Следовательно,
S(G)=∑i=1nS(Gi)=∑i=1n∫xixif2(x)-f1(x))dx==∫x0xn(f2(x)-f(x))dx=∫abf2(x)-f1(x)dx
Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.
Проиллюстрируем на графике общий случай.
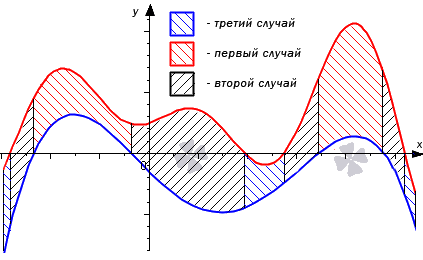
Формулу S(G)=∫abf2(x)-f1(x)dx можно считать доказанной.
А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y=f(x) и x=g(y).
Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.
Необходимо определить площадь фигуры, которая ограничена параболой y=-x2+6x-5 и прямыми линиями y=-13x-12, x=1, x=4.
Решение
Изобразим линии на графике в декартовой системе координат.
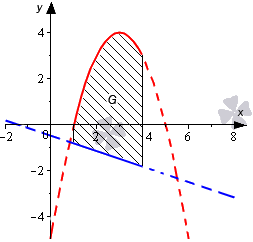
На отрезке [1;4] график параболы y=-x2+6x-5 расположен выше прямой y=-13x-12. В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:
S(G)=∫14-x2+6x-5–13x-12dx==∫14-x2+193x-92dx=-13×3+196×2-92×14==-13·43+196·42-92·4–13·13+196·12-92·1==-643+1523-18+13-196+92=13
Ответ: S(G)=13
Рассмотрим более сложный пример.
Необходимо вычислить площадь фигуры, которая ограничена линиями y=x+2, y=x, x=7.
Решение
В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x=7. Это требует от нас найти второй предел интегрирования самостоятельно.
Построим график и нанесем на него линии, данные в условии задачи.
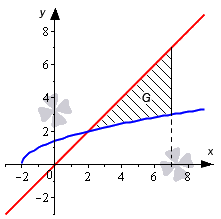
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y=x и полу параболы y=x+2. Для нахождения абсциссы используем равенства:
y=x+2ОДЗ: x≥-2×2=x+22×2-x-2=0D=(-1)2-4·1·(-2)=9×1=1+92=2∈ОДЗx2=1-92=-1∉ОДЗ
Получается, что абсциссой точки пересечения является x=2.
Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y=x+2 , y=x пересекаются в точке (2;2), поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.
На интервале [2;7] график функции y=x расположен выше графика функции y=x+2 . Применим формулу для вычисления площади:
S(G)=∫27(x-x+2)dx=x22-23·(x+2)3227==722-23·(7+2)32-222-23·2+232==492-18-2+163=596
Ответ: S(G)=596
Необходимо вычислить площадь фигуры, которая ограничена графиками функций y=1x и y=-x2+4x-2.
Решение
Нанесем линии на график.
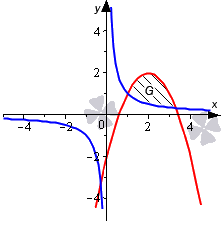
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1x и -x2+4x-2. При условии, что x не равно нулю, равенство 1x=-x2+4x-2становится эквивалентным уравнению третьей степени -x3+4×2-2x-1=0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».
Корнем этого уравнения является х=1: -13+4·12-2·1-1=0.
Разделив выражение -x3+4×2-2x-1 на двучлен x-1, получаем: -x3+4×2-2x-1⇔-(x-1)(x2-3x-1)=0
Оставшиеся корни мы можем найти из уравнения x2-3x-1=0:
x2-3x-1=0D=(-3)2-4·1·(-1)=13×1=3+132≈3.3 ; x2=3-132≈-0.3
Мы нашли интервал x∈1; 3+132, на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:
S(G)=∫13+132-x2+4x-2-1xdx=-x33+2×2-2x-ln x13+132==-3+13233+2·3+1322-2·3+132-ln3+132—133+2·12-2·1-ln 1=7+133-ln3+132
Ответ: S(G)=7+133-ln3+132
Необходимо вычислить площадь фигуры, которая ограничена кривыми y=x3, y=-log2x+1 и осью абсцисс.
Решение
Нанесем все линии на график. Мы можем получить график функции y=-log2x+1 из графика y=log2x, если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у=0.
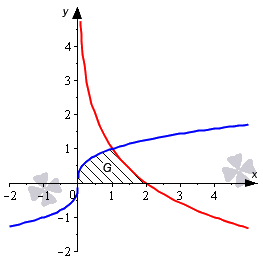
Обозначим точки пересечения линий.
Как видно из рисунка, графики функций y=x3 и y=0 пересекаются в точке (0;0). Так получается потому, что х=0 является единственным действительным корнем уравнения x3=0.
x=2 является единственным корнем уравнения -log2x+1=0, поэтому графики функций y=-log2x+1 и y=0 пересекаются в точке (2;0).
x=1 является единственным корнем уравнения x3=-log2x+1. В связи с этим графики функций y=x3 и y=-log2x+1 пересекаются в точке (1;1). Последнее утверждение может быть неочевидным, но уравнение x3=-log2x+1 не может иметь более одного корня, так как функция y=x3 является строго возрастающей, а функция y=-log2x+1 строго убывающей.
Дальнейшее решение предполагает несколько вариантов.
Вариант №1
Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x∈0; 1, а вторая ниже красной линии на отрезке x∈1;2. Это значит, что площадь будет равна S(G)=∫01x3dx+∫12(-log2x+1)dx.
Вариант №2
Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x∈0; 2, а вторая между красной и синей линиями на отрезке x∈1; 2. Это позволяет нам найти площадь следующим образом:
S(G)=∫02x3dx-∫12×3-(-log2x+1)dx
В этом случае для нахождения площади придется использовать формулу вида S(G)=∫cd(g2(y)-g1(y))dy. Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y.
Разрешим уравнения y=x3 и -log2x+1 относительно x:
y=x3⇒x=y3y=-log2x+1⇒log2x=1-y⇒x=21-y
Получим искомую площадь:
S(G)=∫01(21-y-y3)dy=-21-yln 2-y4401==-21-1ln 2-144–21-0ln 2-044=-1ln 2-14+2ln 2=1ln 2-14
Ответ: S(G)=1ln 2-14
Необходимо вычислить площадь фигуры, которая ограничена линиями y=x, y=23x-3, y=-12x+4.
Решение
Красной линией нанесем на график линию, заданную функцией y=x. Синим цветом нанесем линию y=-12x+4, черным цветом обозначим линию y=23x-3.
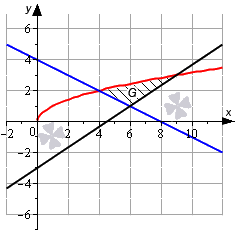
Отметим точки пересечения.
Найдем точки пересечения графиков функций y=x и y=-12x+4 :
x=-12x+4ОДЗ: x≥0x=-12x+42⇒x=14×2-4x+16⇔x2-20x+64=0D=(-20)2-4·1·64=144×1=20+1442=16; x2=20-1442=4Проверка:x1=16=4, -12×1+4=-12·16+4=-4⇒x1=16 не является решением уравненияx2=4=2, -12×2+4=-12·4+4=2⇒x2=4 является решением уравниния ⇒(4; 2) точка пересечения y=x и y=-12x+4
Найдем точку пересечения графиков функций y=x и y=23x-3:
x=23x-3ОДЗ: x≥0x=23x-32⇔x=49×2-4x+9⇔4×2-45x+81=0D=(-45)2-4·4·81=729×1=45+7298=9, x245-7298=94Проверка:x1=9=3, 23×1-3=23·9-3=3⇒x1=9 является решением уравнения ⇒(9; 3) точка пересечания y=x и y=23x-3×2=94=32, 23×1-3=23·94-3=-32⇒x2=94 не является решением уравнения
Найдем точку пересечения линий y=-12x+4 и y=23x-3:
-12x+4=23x-3⇔-3x+24=4x-18⇔7x=42⇔x=6-12·6+4=23·6-3=1⇒(6; 1) точка пересечения y=-12x+4 и y=23x-3
Дальше мы можем продолжить вычисления двумя способами.
Способ №1
Представим площадь искомой фигуры как сумму площадей отдельных фигур.
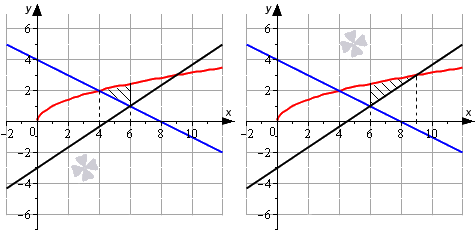
Тогда площадь фигуры равна:
S(G)=∫46x–12x+4dx+∫69x-23x-3dx==23×32+x24-4×46+23×32-x23+3×69==23·632+624-4·6-23·432+424-4·4++23·932-923+3·9-23·632-623+3·6==-253+46+-46+12=113
Способ №2
Площадь исходной фигуры можно представить как сумму двух других фигур.
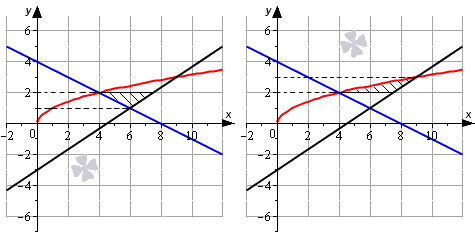
Тогда решим уравнение линии относительно x, а только после этого применим формулу вычисления площади фигуры.
y=x⇒x=y2 красная линияy=23x-3⇒x=32y+92 черная линияy=-12x+4⇒x=-2y+8 синяя линия
Таким образом, площадь равна:
S(G)=∫1232y+92–2y+8dy+∫2332y+92-y2dy==∫1272y-72dy+∫2332y+92-y2dy==74y2-74y12+-y33+3y24+92y23=74·22-74·2-74·12-74·1++-333+3·324+92·3–233+3·224+92·2==74+2312=113
Как видите, значения совпадают.
Ответ: S(G)=113
Итоги
Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:
Пример 10
Вычислить площадь фигуры, ограниченной линиями 
.
И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.
В нашей задаче: прямая 
определяет ось 
, прямые 
параллельны оси 
и парабола 
симметрична относительно оси 
, для неё находим несколько опорных точек:
Искомую фигуру желательно штриховать:
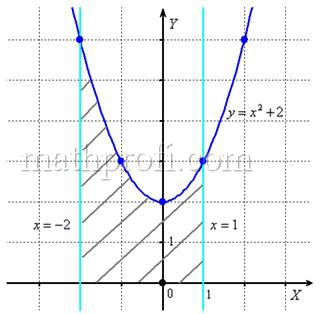
Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке 
график функции 
расположен над осью 
, поэтому искомая площадь:
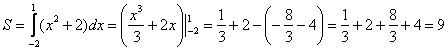
Ответ: 
После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.
И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Пример 11
Вычислить площадь фигуры, ограниченной линиями 
и осью 
Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью 
:
Пример 12
Вычислить площадь фигуры, ограниченной линиями 
, 
и координатными осями.
Решение: найдём несколько опорных точек для построения экспоненты:
и выполним чертёж, получая фигуру площадью около двух клеток:
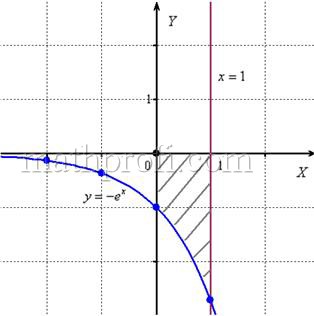
Если криволинейная трапеция расположена не выше оси 
, то её площадь можно найти по формуле: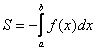 
.
В данном случае: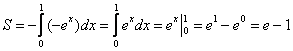 
Ответ: 
– ну что же, очень и очень похоже на правду.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:
Пример 13
Найти площадь плоской фигуры, ограниченной линиями 
, 
.
Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы 
и прямой 
, поскольку здесь будут находиться пределы интегрирования. Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:
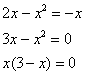
таким образом:
Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».
С прямой 
всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
– именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:
Выполним чертеж:
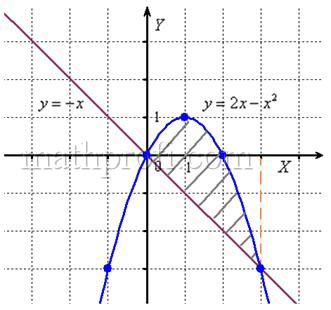
А теперь рабочая формула: если на отрезке 
некоторая непрерывная функция 
больше либо равна непрерывной функции 
, то площадь фигуры, ограниченной графиками этих функций и отрезками прямых 
, можно найти по формуле:
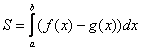
Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.
В нашем примере очевидно, что на отрезке 
парабола располагается выше прямой, а поэтому из 
нужно вычесть 
Завершение решения может выглядеть так:
На отрезке 
: 
, по соответствующей формуле:
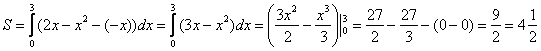
Ответ: 
Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы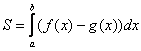 
. Поскольку ось 
задаётся уравнением 
, то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу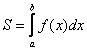 
либо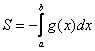 
А сейчас пара типовых задач для самостоятельного решения
Пример 14
Найти площадь фигур, ограниченных линиями:
а) 
, 
.
б) 
, 
, 
Решение с чертежами и краткими комментариями в конце книги
В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:
Пример 15
Вычислить площадь фигуры, ограниченной линиями 
Решение: выполним бесхитростный чертёж,
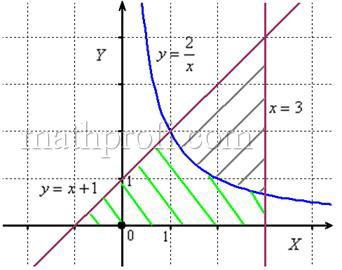
хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую 
можно недочертить до оси 
, и тогда мы вовсе не увидим нужную фигуру.
Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:
1) на отрезке 
над осью 
расположен график прямой 
;
2) на отрезке 
над осью 
расположен график гиперболы 
.
Совершенно понятно, что площади можно (и нужно) сложить:
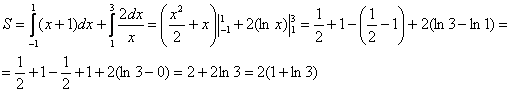
Ответ: 
И познавательный пример для самостоятельного решения:
Пример 16
Вычислить площадь фигуры, ограниченной линиями 
, 
, 
и координатными осями.
Итак, систематизируем важные моменты этой задачи:
На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс 
зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.
Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.
Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой 
и прямой 
, где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:
и находим его корни:
– нижний предел интегрирования, 
– верхний предел.
Во-вторых, не всегда понятен «внешний вид» линии, и функция 
(Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html
После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.
Составляем определённый интеграл или несколько интегралов по формуле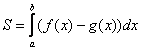 
, все основные вариации мы разобрали выше.
Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.
Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!
1.9. Объём тела вращения
1.7. Геометрический смысл определённого интеграла
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
