-
Главная
-
ГДЗ
- 3 класс
- Математика
-
Моро рабочая тетрадь
- Внетабличное умножение и деление
- Страница 10. Часть 2
Вернуться к содержанию рабочей тетради
Внетабличное умножение и деление
5
6
7
8
9
10
11
12
13
14
15
Вопрос
19. 1) Для детского сада купили 6 красных шаров и 3 синих, по цене 5 р. за каждый. Сколько денег заплатили за все эти шары?
Реши задачу двумя способами, составляя выражения.

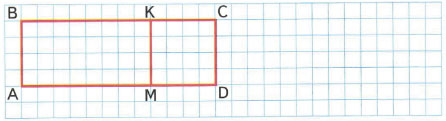
2) Запиши и объясни, как можно найти площадь прямоугольника ABCD, умножая сумму на число, и как можно найти его площадь другим способом.
3) Вычисли значения выражений любым способом.

Подсказка
Если есть схематический рисунок ,таблица или чертёж, краткую запись задачи составлять не нужно.
Площадь прямоугольника равна произведению его длины и ширины.
Чтобы умножить сумму на число, можно вычислить сумму и умножить её на число или умножить на число каждое слагаемое и полученные результаты сложить.
Ответ
5
6
7
8
9
10
11
12
13
14
15


5
6
7
8
9
10
11
12
13
14
15
Вернуться к содержанию рабочей тетради
Содержание
- Площадь фигуры
- Сравнение площадей фигур
- Сравнение площадей способом наложения
- Сравнение площадей заданной меркой
- Единицы площади
- Квадратный сантиметр
- Квадратный дециметр
- Квадратный метр
- Квадратный километр
- Квадратный миллиметр
- Ар
- Гектар
- Математика. 3 класс
- Математика. 3 класс
- Конспект урока по математике на тему «Площадь» (3 класс) М.И, Моро
- Как найти площадь прямоугольника 3 класс
Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.


Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник : 
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
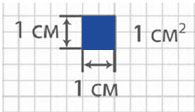
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
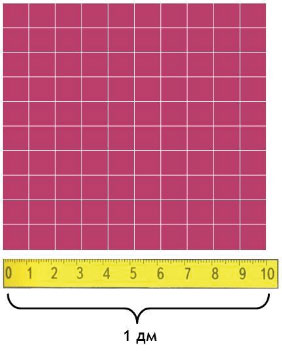
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
Значит, 1 дм² = 100 см²
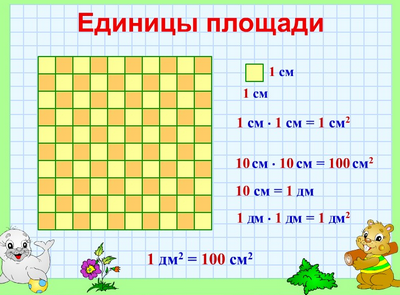
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
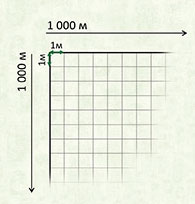
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
Квадратный миллиметр
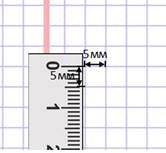
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
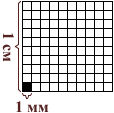
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
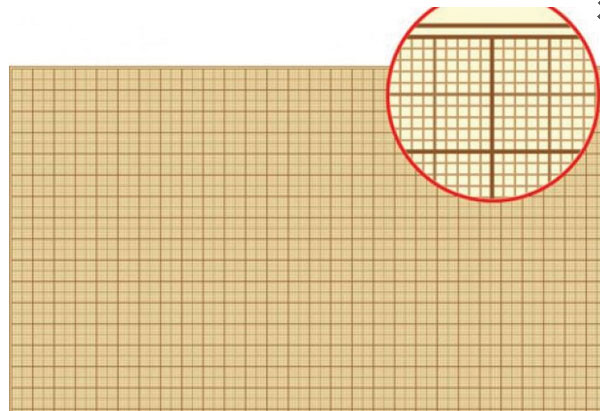
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Слово «ар» при числах сокращённо записывают так:
Гектар
Слово «гектар» при числах сокращённо записывают так:
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Поделись с друзьями в социальных сетях:
Источник
Математика. 3 класс
Конспект урока
Математика, 3 класс
Урок №21. Площадь. Способы сравнения фигур по площади. Единица площади – квадратный сантиметр
Перечень вопросов, рассматриваемых в теме:
— что такое площадь фигуры?
— какие есть способы сравнения фигур по площади?
— что такое квадратный сантиметр?
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 56-59.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.:Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС. М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Сравним фигуры и расставим их в порядке убывания их площади.







Фигуры расположили в следующем порядке: 4, 2, 1, 6, 5, 3.
В математике говорят: площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией. Когда мы сравниваем площади фигур, мы выясняем, больше или меньше места занимает данная фигура на плоскости. Мы сравнивали эти фигуры способом, который называется «на глаз».
Сравним фигуры и выясним, площадь какой фигуры больше.

Способом сравнения на глаз, определить площадь какой фигуры невозможно.
Для этого существует способ сравнения: наложения.

Вывод: площадь прямоугольника больше площади круга.
Сравним две фигуры.

Изученными способами сравнить площади не получается. Есть еще один способ сравнения: подсчет количества одинаковых мерок.
Задания тренировочного модуля:
1.Выберите правильное высказывание:
1. сумма длин всех сторон
2. внутренняя часть фигуры
2. внутренняя часть фигуры
2. Выделите фигуры с одинаковой площадью.
Источник
Математика. 3 класс
Конспект урока
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.

Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.

Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см 2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
Источник
Конспект урока по математике на тему «Площадь» (3 класс) М.И, Моро
Конспект урока по математике в 3 классе.
· Дать представление о площади фигур, познакомить с различными способами сравнения фигур: «на глаз»; путем наложения одной фигуры на другую; с использованием различных единиц измерения площадей.
· Закрепить знания свойств геометрических фигур.
· Закрепить умение точно производить измерения и чертить квадрат и прямоугольник.
· Закрепить знания изученных таблиц умножения и соответствующих случаев деления.
· Развивать логическое мышление и пространственное воображение.
· Закрепить умение решать задачи.
· Воспитывать аккуратность при выполнении работы.
· Поиск и выделение необходимой информации.
· Умение осознанно и произвольно строить речевое высказывание.
· Анализ объектов с целью выделения признаков (существующих/несуществующих)
· Самостоятельное создание способов решения проблем творческого и поискового характера.
· Самостоятельно находить несколько вариантов решения учебной задачи, представленной на наглядно-образном, словесно-образном и словесно-логическом уровнях.
· Контролировать и оценивать свои действия в работе с учебным материалом при сотрудничестве с учителем и одноклассниками.
· Допускать возможность существования различных точек зрения, в том числе не совпадающих с собственной и ориентироваться на позицию партнера в общении и взаимодействии
· Строить сообщение в соответствии с учебной задачей
· Адекватно использовать средства устной речи для решения различных коммуникативных задач.
· Формировать интерес к изучению математики.
· Формировать мотивацию к обучению и целенаправленной познавательной деятельности.
· Формировать умение оценивать свои поступки в соответствии с определенной ситуацией.
· Для учителя: конспект урока; наглядный материал (карточки с заданиями, геометрические фигуры, примеры, ответы с буквами, карточка « S », изображения Незнайки и его друзей); музыкальная физкультминутка «От Незнайки» с сайта YouTube
· Для учащихся: учебник математики 3 класс М.И. Моро; рабочая тетрадь; ручка, линейка, карандаш, ластик; геометрические фигуры (два квадрата, два прямоугольника); пазлы в конверте.
— Сегодня у нас необычный урок, а волшебный. К нам на урок пришли сказочные герои и они приглашают нас в сказочное путешествие в мир «Геометрических фигур», чтобы узнать много нового и интересного (на доске герои из Цветочного города)
— Ребята, вы узнали кто это, кто наши сегодняшние волшебные гости?
(это Незнайка и его друзья)
Итак, начнем наше путешествие (на доске карточки с заданиями от сказочных друзей)
— Знайка и Незнайка предлагают нам начать с …
· Найдите сумму чисел 50 и 24? (50+24=74)
Назовите компоненты сложения? (слагаемое, слагаемое, сумма)
· Найдите разность чисел 98 и 26? (98-26=72)
Назовите компоненты вычитания? (уменьшаемое, вычитаемое, разность)
· Увеличьте 5 в 3 раза? (5*3=15)
Назовите компоненты умножения? (множитель, множитель, произведение)
· Уменьшите 36 в 6 раз? (36:6=6)
Назовите компоненты деления? (делимое, делитель, частное)
· Три бельчонка маму-белку
Им на завтрак мама-белка
Разделила на троих.
Сколько каждому из них? (30:3=10)
— Молодцы! Справились на отлично!
3. Работа с геометрическим материалом.
— Следующее задание от Ворчуна (карточка)
Он предлагает нам собрать ПАЗЛ. (у детей на парте лежат пазлы, из которых они должны собрать картинку. Дети собирают картинку и как только они собрали, учитель вывешивает на доску такое же изображение)
— Что вы видите на картинке, что у вас получилось? (Паровозик)
— Из чего он состоит? (из геометрических фигур)
— Назовите их? (треугольник, круг, квадрат и прямоугольник)
— Какие еще геометрические фигуры вы знаете? (ответы детей)
— Обратим внимание на наш паровозик. Какие из геометрических фигур будут лишними? (круг) (ИСКЛЮЧЕНИЕ ЛИШНЕГО)
— Почему вы исключили круг? (так как у круга, в отличии от других фигур нет углов)
— Да, совершенно верно!
(Учитель обращает внимание и показывает на треугольник)
— Что это за фигура? (треугольник)
— Почему это треугольник? Назовите его признаки? (Треугольник – это геометрическая фигура, у которой три стороны и три угла)
(Учитель обращает внимание и показывает квадрат)
— А это что за фигура? (квадрат)
— Назовите признаки квадрата? (Квадрат – это геометрическая фигура, у которой все стороны равны и углы прямые)
(Учитель обращает внимание и показывает прямоугольник)
— А это? (прямоугольник)
— Назовите признаки прямоугольника? (Прямоугольник – это четырехугольник у которого все углы прямые и противоположные стороны равны)
— Что мы можем узнать у этих фигур, у треугольника, квадрата и прямоугольника? (можем измерить длины их сторон)
— Хорошо. А если мы знаем длины сторон фигуры, что мы еще можем найти? (периметр)
— Что такое периметр? (Периметр – это сумма длин всех сторон)
(Учитель предлагает измерить длины сторон квадрата и прямоугольника, и найти их периметр)
— Ребята, а как вы думаете, что еще мы можем узнать у квадрата и прямоугольника? (ответы детей)
— Это мы и узнаем на нашем сегодняшнем уроке.
— А сначала мы немножко отдохнём.
— Знайка и Незнайка предлагают нам интересную и подвижную музыкальную паузу.
(дети под музыку выполняют ряд физических упражнений)
— Молодцы! Хорошо отдохнули, даже немного взбодрились и готовы продолжить наше волшебное путешествие.
— И следующее задание от Стекляшкина (карточка)
(ОПРЕДЕЛЕНИЕ ТЕМЫ УРОКА)
(на доске вывешены карточки с примерами и карточки с ответами на эти примеры, в карточках с ответами спрятана буква)
— Итак, что же у нас получилось? (ПЛОЩАДЬ)
— Назовите мне орфограммы в этом слове? (ЧА-ЩА, смягчительный Ь, парная согласная в корне слова «Д», проверочное слово «ПЛОЩАДИ»)
— Назовите количество букв и количество звуков в этом слове? (7 букв, 6 звуков)
— Почему звуков меньше? (Ь звука не дает)
— Итак, у квадрата и прямоугольника, кроме периметра мы можем найти еще и площадь.
— Что такое площадь, как вы думаете? (ответы детей)
(можно привести пример с классной доской или с самой классной комнатой)
6. Работа с геометрическим материалом по теме урока
— Итак, Незнайка предлагает нам поработать с некоторыми парами геометрических фигур (карточка)
(Учитель вывешивает на доску геометрические фигуры, такие же геометрические фигуры лежат на партах у детей. Красный и зеленый квадраты. Красный квадрат должен быть больше чем зеленый. А также два одинаковых прямоугольника. Один синий, другой фиолетовый)
(Учитель вначале обращает внимание детей на квадраты)
— Посмотрите на эти квадраты, что вы можете сказать? (красный квадрат больше чем зеленый)
— Как вы это узнали, что вы для этого сделали? (посмотрели, «на глаз», наложили одну фигуру на другую)
— Можно сделать вывод, что площадь красного квадрата больше площади зеленого квадрата, т.к. зеленый квадрат полностью вместился в красный.
(Учитель обращает внимание детей на прямоугольники)
— Посмотрите на эти прямоугольники, что вы можете сказать о них? (они равны)
— Как вы узнали? (посмотрели, «на глаз», наложили одну фигуру на другую)
— Из этого, можно сделать вывод, что площади синего и фиолетового прямоугольника равны, т.к. они полностью совпали.
— А теперь, давайте сравним площади квадрата и прямоугольника.
— Можем ли мы определить площадь какой фигуры больше, а какой меньше «на глаз»? (нет)
— А попробуйте наложить одну фигуру на другую, получается сравнить? (нет)
— Получается, что «на глаз» сравнить фигуры не получается, потому что они разные по форме, да и методом наложения одной фигуры на другую не получается, потому что ни одна, ни другая не помещаются друг в друге.
— Так как же нам сравнить площади этих фигур? (ответы детей)
— Назовите общее у квадрата и прямоугольника? (4 стороны, 4 вершины, 4 угла, углы прямые)
— Чем отличается квадрат от прямоугольника? (у квадрата все стороны равны, а у прямоугольника только противоположные стороны равны)
— Измерьте сторону квадрата, чему она равна? (12 см)
— Начертите в тетради квадрат со стороной, которая будет в 3 раза меньше.
— С какой стороной мы начертим квадрат в тетради? (4 см.)
— Укажите на чертеже длину стороны квадрата.
— А теперь измерим стороны прямоугольник, чему они равны? (9 см. и 15 см.)
— Давайте отступим три клеточки вправо и начертим прямоугольник со сторонами в три раза меньше.
— Это значит, с какими длинами сторон мы начертим прямоугольник? (3 см. и 5 см.)
— Укажите на чертеже длины сторон прямоугольника.
 4 см. 5 см.
4 см. 5 см.

— Итак, начертив фигуры в тетради, мы разбили их на одинаковые фигуры меньшего размера – клетки тетради.
— Можно их посчитать (1 вариант считает клетки в квадрате, 2 вариант – в прямоугольнике)
— Сколько клеток поместилось в квадрате? (64) А в прямоугольнике? (60) Сравните эти числа? (64>60)
— Сделайте вывод? (площадь квадрата больше площади прямоугольника)
— Да, совершенно верно, большую площадь имеет та фигура, которая содержит большее количество клеток.
— Но площадь фигур, ребята, можно измерить и другими мерками.
(Учитель демонстрирует (переворачивает эти же квадрат и прямоугольник) что квадрат и прямоугольник разбиты на одинаковые квадраты со стороной 1см.
— Как удобнее посчитать эти маленькие квадратики? (ответы детей)
(просто посчитать à посчитать сколько в одном ряду и сложить à заменить умножением сложение одинаковых слагаемых)
— Давайте запишем результат в тетрадь.
— Площадь, мы будем обозначать так… S (учитель вывешивает на доску карточку с обозначением площади)
— Под квадратом – 4+4+4+4=4*4=16
— Что такое 4 и 4? (это длины сторон)
— Под прямоугольником – 5+5+5=5*3=15
— Что такое 5 и 3? (это длины сторон)
— Сделаем вывод…как найти площадь квадрата и прямоугольника? (нужно длину одной стороны, умножить на длину другой стороны)
7. Подведение итогов урока
— Знайка и Незнайка предлагают подвести итог нашего сегодняшнего волшебного путешествия в мир «Геометрических фигур» и ответить на некоторые вопросы, которые они для вас подготовили.
(у детей на партах лежат карточки с вопросами)
— О чем мы говорили на сегодняшнем уроке? (о геометрических фигурах)
— Что мы вспомнили о таких геометрических фигурах как круг, треугольник, квадрат и прямоугольник? (у круга нет углов, этим он и отличается от остальных геометрических фигур; у треугольника три стороны, три вершины, три угла; у квадрата все стороны равны и углы прямые; а у прямоугольника противоположные стороны равны и углы тоже прямые)
— А что узнали нового? (что кроме периметра, у геометрических фигур мы можем найти еще и площадь)
— Чему же научились мы с вами сегодня? (находить площадь квадрата и прямоугольника)
— Как же мы ее будем находить? (нужно длину одной стороны умножить на длину другой стороны)
— Молодцы, совершенно верно!
— А теперь, ребята оценим наш сегодняшний урок
— У каждого из вас есть три кружочка: (у детей, у каждого есть кружок с красной звездочкой, желтым квадратиком и зеленым треугольником)
ЗВЕЗДОЧКА – она означает, что сегодня на уроке вам понравилось и было все понятно и доступно.
КВАДРАТИК – значит то, что вам понравилось на уроке, но остались моменты, которые вы не поняли и вам нужно объяснить дополнительно.
ТРЕУГОЛЬНИК – вам вовсе не понравилось и ничего вам было не понятно.
— Поднимите, пожалуйста, вверх тот кружок, на котором нарисована та фигурка, которая и означает то, как прошел для вас наш сегодняшний необычный урок.
(дети поднимают вверх выбранную фигурку)
-Большое спасибо вам за работу на уроке, за ваши знания, умения и искрящие глаза.
Источник
Как найти площадь прямоугольника 3 класс
Названия геометрических фигур происходят от количества их сторон. Например, треугольник, четырехугольник, пятиугольник. Но есть фигуры, которые названы по другим признакам, например, прямоугольник, квадрат, ромб, трапеция. Все эти фигуры — четырехугольники, но отличаются друг от друга величиной углов и сторон.
Квадрат — прямоугольник, у которого все углы по 90 градусов и стороны равные.
Такие отличия есть и у других фигур, например, треугольники подразделяются на прямоугольные, равносторонние, равнобедренные и разносторонние. Свойства фигуры зависят как от количества сторон, так и от других характеристик — величины углов и сторон. Только измерив все параметры, можно точно описать фигуру и определить, какими формулами и правилами пользоваться при вычислениях.
Под этим термином понимают часть плоскости, ограниченной несколькими замкнутыми (соединенными) линиями. В результате соединения линий образуется отрезки, которые называются сторонами фигуры и точки соприкосновения, которые носят название вершин. У треугольника три стороны и три вершины, у четырехугольника — четыре стороны и четыре вершины.
В геометрии есть фигуры, которые выпадают из этого ряда. Это точка, прямая линия, отрезок, луч. Отличаются они от остальных фигур, тем, что не занимают никакой площади, это просто части линии.
Что такое площадь
Теперь рассмотрим еще одно понятие геометрии — площадь. Это часть плоскости, которая находится внутри многоугольника. Другими словами, все, что находится между сторонами фигуры и является ее площадью. Геометрия — часть математики, то есть, наука точная, которая стремится все измерить и описать цифрами. Не стала исключением и площадь. Часть плоскости, которая находится внутри фигуры, разбили на маленькие части с равными сторонами, идущими под прямым углом друг к другу. Такая фигура называется квадрат.
Квадрат — геометрическая фигура из четырех равных сторон и четырех прямых углов.
Расчет площади прямоугольника
Разберем простую задачу — как высчитать площадь прямоугольника? Можно решить ее двумя способами. Самый простой, но самый длинный и трудоемкий — нарисовать прямоугольник и с помощью карандаша и линейки разбить его на маленькие квадратики. Затем посчитать количество квадратиков и узнать, сколько их поместилось внутри.
Такой способ простой и доступный, если длина сторон прямоугольника — целое количество сантиметров или метров. А вот при их нецелом количестве, например стороны три с половиной и четыре с половиной сантиметра (3,5 см и 4,5 см), посчитать сложнее. Еще сложнее, если стороны, например 3см и 2 мм и 4 см и 7 мм. Рисовать придется миллиметровые квадратики, что довольно сложно и долго.
Ученые древности, идя таким путем заметили интересную особенность, если посчитать квадраты внутри фигуры и сравнить их с результатом умножения длин сторон прямоугольника, то они окажутся одинаковыми. Проверив это на многих прямоугольниках и квадратах составили правило:
Площадь прямоугольника равна длине умноженной на ширину.
В учебниках можно найти и другую формулировку — площадь прямоугольника равна произведению соседних сторон, или еще иначе — площадь прямоугольника равна произведению основания на высоту. Суть этих утверждений одна и та же. Выражается она в формуле:
S=AB ∙BC.
Использование этой формулы — самый простой способ, как вычислить площадь прямоугольника с разными сторонами. Подходит он и для решения задачи вычисления квадрата (прямоугольника с равными сторонами). Для квадрата формула может выглядеть несколько иначе.
S=АВ 2
Периметр
Еще одна важная характеристика прямоугольника — периметр. Это сумма длин всех сторон. Периметр легко найти, измерив все стороны и сложив результаты. Но, как и в случае с площадью, лучше воспользоваться формулой. Сначала найдем периметр квадрата:
Р = АВ+ВС+СD+AD.
Но у квадрата все стороны одинаковые, значит, выражение можно записать иначе:
Р= АВ+АВ=АВ=АВ = 4 ∙ АВ, или 4АВ.
Для прямоугольника с разными сторонами периметр находится по такой же формуле:
Р = АВ+ВС+СD+AD.
Но здесь равны не все стороны, а только противоположные:
АВ= СD и ВС= AD
Перепишем начальную формулу по-другому:
Р= (АВ +СD) и (ВС + AD). Из равенства сторон получим Р=2АВ+2ВС + 2(АВ+ВС). Словами это будет звучать так:
Периметр прямоугольника равен сумме соседних сторон умноженной на два.
Как видно из приведенных утверждений, площадь и периметр прямоугольника можно вычислить двумя способами — непосредственным измерением и вычислением. Второй способ намного удобнее, особенно, если приходится находить площади и периметры реальных участков, например, площадки под строительство, дачного участка, комнаты.
Смотрите также другие геометрические фигуры:
Источник
Математика 3 класс рабочая тетрадь Моро, Волкова 2 часть ответы – страница 10

- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И.
- Год: 2021.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Подготовили готовое домашнее задание к упражнениям на 10
странице по предмету математика за 3 класс. ➜ Ответ на задание: 19.
-1.jpg)
Рабочая тетрадь 2 часть – Страница 10.
Ответы 2022 года.
Номер 19.
1) Для детского сада купили 6 красных шаров и 3 синих, по цене 5 р. за каждый. Сколько денег заплатили за все эти шары?
Реши задачу двумя способами, составляя выражения.
Ответ:
-2.jpg)
2) Запиши и объясни, как можно найти площадь прямоугольника ABCD, умножая сумму на число, и как можно найти его площадь другим способом.
Ответ:
-3.jpg)
3) Вычисли значения выражений любым способом.
Ответ:
-4.jpg)
Комментарии
Периметр данного многоугольника можно найти сложив длинны всех его сторон, но для начала придётся найти длинны двух сторон – АВ и АК:
АВ = CD + EK = 2 + 1 = 3 см
AK = BC + DE = 4 + 2 = 6 см
Теперь можно найти периметр всей фигуры:
Р = AB + BC + CD + DE + EK + AK = 3 + 4 + 2 + 2 + 1 + 6 = 18 см
Площадь же многоугольника можно найти, как минимум пятью способами ( правда не уверен, что в третьем классе уже умеют находить площадь трапеций по длинам оснований и высоте – в данном случае трапеции ABCD и ADEK ). Для того, чтобы проще описать способы решения я добавил на чертёж ещё три точки ( впрочем, для разных вариантов решения не все точки потребуются одновременно ).
Вот такой чертёжик у меня получился

Проще всего найти площадь этой фигуры так
S = S(ABEK) – S(CDEH) = AB * AK – CD * DE = 3 * 6 – 2 * 2 = 18 – 4 = 14 см²
Второй способ:
S = S(ABCG) + S(DEGK) = AB * BC + DE * EK = 3 * 4 + 2 * 1 = 12 + 2 = 14 см²
Третий способ:
S = S(BCDF) + S(AFEK) = BC * CD + AK * EK = 4 * 2 + 6 * 1 = 8 + 6 = 14 см²
Четвёртый способ:
S = S(BCDF) + S(AFDG) + S(DEKG) = BC * CD + AG * AF + DE * EK = 4 * 2 + 4 * 1 + 2 * 1 = 8 + 4 + 2 = 14 см²
Ну, и, наконец, пятый способ с трапециями ( извиняюсь, забыл провести на чертеже ещё и AD, впрочем в решении его величина не важна ):
S = S(ABCD) + S(ADEK) = BC * ( AB + CD )/2 + EK * ( DE + AK )/2 = 4 * ( 3 + 2 )/2 + 1 * ( 2 + 6 )/2 = 10 + 4 = 14 см²
Ответ: периметр многоугольника равен 18 см, а его площадь – 14 см²
1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.

2) Найди двумя способами площадь прямоугольника ABCD.

reshalka.com
ГДЗ учебник по математике 3 класс Моро. Часть 1. Страница 86. Номер №8
Решение 1
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
S
B
C
K
E
=
B
C
∗
C
K
=
2
∗
2
=
4
(
с
м
2
)
;
S
A
E
K
D
=
E
K
∗
K
D
=
2
∗
3
=
6
(
с
м
2
)
.
Решение 2
Способ 1.
AB = CD = 5 см;
BC = AD = 2 см;
S
A
B
C
D
=
A
B
∗
A
D
=
5
∗
2
=
10
(
с
м
2
)
.
Способ 2.
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
S
B
C
K
E
=
B
C
∗
C
K
=
2
∗
2
=
4
(
с
м
2
)
;
S
A
E
K
D
=
E
K
∗
K
D
=
2
∗
3
=
6
(
с
м
2
)
;
S
A
B
C
D
=
S
B
C
K
E
+
S
A
E
K
D
=
4
+
6
=
10
(
с
м
2
)
.
