Как перевести длину периметра в площадь — математический — 2022
Периметр фигуры — это общее расстояние вокруг нее, а площадь — это количество поверхности, которую фигура использует или покрывает. Методы расчета периметра и площади отличаются для каждого вида фигуры. Например, хотя вы можете найти площадь прямоугольника, просто умножив его длину на ширину, круг требует более сложных вычислений. Научитесь преобразовывать периметры самых основных фигур в области, и в дальнейшем вы сможете переходить к составным фигурам.
Квадратные Периметры
Разделите периметр на четыре
Разделите периметр на четыре, чтобы получить длину каждой стороны, так как все четыре стороны квадрата равны. Например, квадрат с периметром 36 дюймов будет иметь стороны размером 9 дюймов каждая, потому что 36 ÷ 4 = 9.
Квадрат длина стороны
Квадрат длины одной стороны. Для квадрата с 9-дюймовыми сторонами, получится 9 х 9 = 81.
Добавить единицу измерения
Добавьте правильную единицу измерения к области. Квадрат с периметром 36 дюймов имеет площадь 81 квадратный дюйм.
Периметры прямоугольника
Отработка длины основания и высоты
Определите длину как основания, так и высоты. Это стороны, которые не параллельны друг другу. Например, скажем, у вас есть прямоугольник с основанием 6 см и высотой 7 см.
Умножить базу на высоту
Умножьте базу на высоту. Тренируйся 6 х 7 = 42.
Добавить единицу измерения
Добавьте правильную единицу измерения. В этом примере площадь прямоугольника составляет 42 см квадратных сантиметров.
Периметры треугольника
Отработать длину базы
Определите длину основания треугольника. Например, скажем, у вас есть треугольник с основанием 3 фута.
Высота тренировки
Рассчитайте высоту треугольника. Скажем, у вас есть треугольник с высотой 12 футов.
Умножить базу на высоту
Умножьте длину основания на длину высоты. Тренируй 3 х 12 = 36.
Разделить на два
Разделите на два. Отработать 36 ÷ 2 = 18.
Добавить единицу измерения
Добавьте правильную единицу измерения. Площадь треугольника составляет 18 квадратных футов.
Окружность окружности
Разделить периметр на пи
Разделите периметр круга, также известный как окружность, на pi (3.14159265), чтобы получить диаметр круга. Например, скажем, у вас есть круг с окружностью 40 дюймов. Отработка 40 ÷ 3.14159265 = 12.732.
Разделите диаметр на два
Разделите диаметр на два, чтобы получить длину радиуса. Отработать 12, 732 ÷ 2 = 6, 366.
Умножить радиус
Умножьте радиус на себя. В этом примере получится 6, 366 х 6, 366 = 40, 526.
Умножить на пи
Умножьте на pi (3.14159265). Отработка 40, 526 х 3, 14159265 = 127, 316.
Добавить единицу измерения
Добавьте правильную единицу измерения. Площадь круга составляет 127, 316 квадратных дюймов.
Как рассчитать площадь от периметра

Недвижимость разбита на лоты. Эти участки чаще всего имеют прямоугольную форму. Из распространенных форм только площадь прямоугольника рассчитывается путем измерения только периметра партии. Определение площади участка также называется определением площади участка. Люди используют площадь .
Как перевести площадь круга в квадратные футы
Хотя может показаться странным сказать, круги измеряются в квадратных единицах. Область круга требует возведения в квадрат своего радиуса, который является прямой линией от ее начала или координат центра до ее края или окружности. Умножение единицы измерения на себя приводит к тому, что эта единица становится квадратной; при умножении .
Как перевести площадь в квадратные футы

Международная система единиц — иначе известная как метрическая система — определяет квадратный метр как единицу площади. В противоположность этому в США обычно используются такие единицы, как квадратные футы или квадратные ярды. С помощью простых математических уравнений вы можете преобразовать измерения площади в квадратные футы.
Через периметр и одну из сторон
Формула расчёта площади прямоугольника и квадрата через периметр и одну из сторон Вам необходимо указать сторону прямоугольника или квадрата (a или b) и периметр, который рассчитывается по формуле P=2*a+2*b. Расчёт происходит по формуле 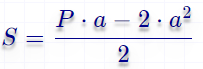 .
.
Калькулятор расчёта площади прямоугольника и квадрата через периметр и одну из сторон, онлайн
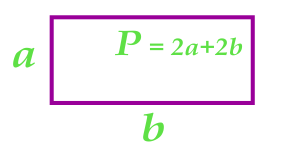 Другой способ
Другой способ
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Калькулятор вычисления периметра и площади геометрических фигур
Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.
Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.
Окружность — это множество точек на плоскости, которые равноудалены от центра на некоторое расстояние, называемое радиусом. Многие считают круг и окружность синонимами, однако это не так. Круг — это часть плоскости, ограниченная окружностью. Вы можете отыскать периметр и площадь круга, но у окружности найти можно только длину, так как она представляет собой кривую, не имеющую площади. Длина окружности или периметр круга находятся по простой формуле:
где R – радиус фигуры.
Площадь круга рассчитывается согласно следующему выражению:
Круги часто встречаются в реальной жизни. В основном это основания цилиндрических и конических деталей, а также просто круглые поверхности, например, круглые столики, диски, грампластинки или катушки. Вид окружности имеют колеса, обручи или кольца. В трехмерной реальности окружность превращается в сферу, а круг — в шар. Форму этих геометрических тел имеют многие реальные и природные объекты. Благодаря своей эффективности круг охватывает максимальную площадь при минимальном периметре. Именно поэтому форму шара имеют капли, снежные комья, метеориты или планеты.
Треугольник
Треугольник — первая гармоничная фигура на плоскости, ограниченная тремя отрезками. Свойства треугольника известны людям с античных времен: изучение фигуры стартовало в Древнем Египте и не завершено до сих пор. Огромный вклад в изучение свойств фигуры внесли Евклид, Эйлер и Лобачевский, но даже сегодня продолжается работа над поиском замечательных точек треугольника, которых на данный момент найдено более 6 тысяч. Для определения периметра фигуры достаточно сложить длины всех сторон треугольника по формуле:
где a, b, c – стороны.
Для вычисления площади треугольника используется 5 различных формул плюс нахождение площади через определенный интеграл. Самое простое выражение для вычисления площади:
где a — сторона треугольника, h — его высота.
Наш калькулятор позволяет отыскать площадь или периметр треугольника, зная разные комбинации нескольких параметров, таких как углы, стороны или радиусы связанных окружностей.
Треугольники не слишком распространены в реальной повседневности. В природе они практически не встречаются, за исключением кристаллических решеток некоторых молекул или формы ушей у рыси. А вот в технике, геометрии и прикладных науках треугольник — царь и бог. Наибольшее применение находит следующий тип фигуры.
Прямоугольный треугольник
Прямоугольный треугольник — особая вариация фигуры, у которой две стороны обязательно образуют прямой угол. Эти стороны называются катетами, а противолежащая им сторона — гипотенузой. Соотношение катетов и гипотенузы лежит в основе евклидовой геометрии — эти соотношения определяются теоремой Пифагора. Изучение свойств прямоугольного треугольника положило начало одному из важных разделов математики — тригонометрии, которая используется в самых разных прикладных сферах от компьютерных игр до океанографии.
Формулы для вычисления периметра и площади прямоугольного треугольника ничем не отличаются от формул для обычных вариаций данной фигуры или вытекают из них.
Трапеция
Трапеция, как и слово трапеза, по-гречески означают «стол». Это плоская фигура, ограниченная четырьмя прямыми, две из которых параллельны, а две — нет. По сути, это выпуклый четырехугольник, поэтому параллелограмм и прямоугольник считаются частными случаями трапеции. В общем случае все стороны трапеции имеют разную длину, и для вычисления периметра используется формула:
a, b, c и d – стороны четырехугольника.
Площадь фигуры определяется как:
где a и b – параллельные стороны трапеции, h – высота.
Трапеция очень часто встречается в рукотворном мире. Грани многих предметов имеют вид этого четырехугольника, а буквально трапецеидальную форму имеют такие объекты как автомобильные окна, паруса, скаты крыш или юбки.
Параллелограмм
Параллелограмм — это элегантный четырехугольник, пары сторон которого параллельны друг другу. Любой четырехугольник становится параллелограммом, если его противолежащие стороны параллельны, диагонали в точке пересечения разделяются пополам, а противоположные углы равны. Для вычисления периметра параллелограмма используется простая формула, которая иллюстрирует сумму попарно равных сторон:
Площадь параллелограмма не зависит от величины его углов, и находится по следующей формуле:
Параллелограммы часто встречаются в реальной жизни: это грани многих призматических объектов, очертания полей, спортивных площадок или клумб. Форму параллелограммов имеют практически все отделочные материалы: плитка, кафель, гипсокартон, паркет. Такое разнообразие обусловлено тем, что частными случаями параллелограмма являются прямоугольник, ромб и квадрат, формулы для определения периметров и площадей которых аналогичны или выводятся из теоремы Пифагора.
Частные случаи
Ромб — четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.
Прямоугольник — это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.
Квадрат — это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.
Многоугольник
Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:
- — пентагон; — гексагон;
- восемь — октагон;
- двенадцать — додекагон.
И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:
где n – количество сторон многоугольника, a – длина стороны.
Для определения площади используется выражение:
S = n/4 × a 2 × ctg(pi/n).
Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.
Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.
Примеры из реальной жизни
Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.
Покраска забора
Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Отделка бахромой
Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:
Таким образом, нам понадобится 4 м бахромы для отделки платка.
Заключение
Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
Как найти площадь, зная периметр
Площадь и периметр фигуры являются основными ее геометрическими параметрами. Их нахождение и описание с учетом известных величин составляет значительную долю в обучающем процессе. В общем смысле периметр – это длина всех границ фигуры. Для прямоугольника он равен сумме длин его сторон. А площадь представляет собой всю внутреннюю часть фигуры, измеренной в определенных единицах. Согласно свойствам фигур, а также формулам площади и периметра, можно найти соотношения между этими параметрами фигуры и выразить одно значение из другого. Для определения площади прямоугольника с известным периметром необходимо дополнительно знать одну его сторону.

Инструкция
Запишите известные параметры прямоугольной фигуры. Помимо периметра, для нахождения площади должна быть известна еще одна величина – любая сторона прямоугольника.

Согласно формуле, периметр прямоугольника находится, как сумма всех его сторон. Так как в прямоугольнике противолежащие стороны равны, можно записать формулу периметра: Р = (d+c)*2, где d и c являются прилегающими сторонами фигуры.
Площадь прямоугольной фигуры определяется произведением двух ее прилегающих сторон: S = d*c. Таким образом, зная одну из сторон можно легко найти площадь фигуры.
Подставьте в формулу периметра известные величины: одну из сторон и периметр. Выразите из полученного уравнения вторую неизвестную сторону и вычислите ее. Подставьте полученное значение в формулу площади. Вычислите искомое значение S – площади фигуры.
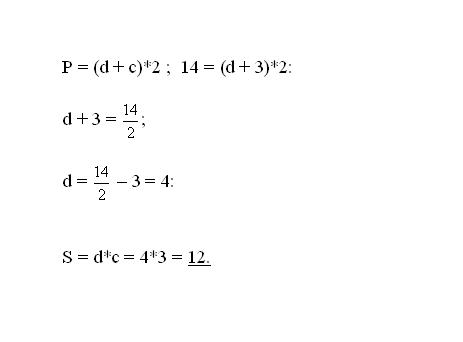
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Загрузить PDF
Загрузить PDF
Очень легко вычислить площадь правильного треугольника (это многоугольник!) и очень непросто сделать это в случае неправильного одиннадцатиугольника (это тоже многоугольник!). Данная статья расскажет вам, как вычислять площадь различных многоугольников.
-

1
Формула для нахождения площади правильного многоугольника: Площадь = 1/2 х периметр х апофема.
- Периметр – сумма сторон многоугольника.
- Апофема – отрезок, соединяющий центр многоугольника и середину любой из его сторон (апофема перпендикулярна стороне).
-

2
Найдите апофему. Она, как правило, дана в условии задачи. Например, дан шестиугольник, апофема которого равна 10√3.
-

3
Найдите периметр. Если периметр не дан в условии задачи, то его можно найти по известной апофеме.
- Шестиугольник можно разбить на 6 равносторонних треугольников. Апофема делит одну сторону пополам, создавая прямоугольный треугольник с углами 30-60-90 градусов.
- В прямоугольном треугольнике сторона, противолежащая углу в 60 градусов, равна x√3; углу в 30 градусов равна «х»; углу 90 градусов равна 2x. Если значение стороны x√3 равно 10√3, то х = 10.
- «х» – это половина длины основания треугольника. Удвойте ее и найдете полную длину основания. В нашем примере основание треугольника равно 20 единицам. В свою очередь основание треугольника есть сторона шестиугольника. Таким образом, периметр шестиугольника равен 20 х 6 = 120.
-

4
Подставьте значения апофемы и периметра в формулу. В нашем примере:
- площадь = 1/2 х 120 х 10√3
- площадь = 60 х 10√3
- площадь = 600√3
-

5
Упростите ответ. Возможно, вам придется записать ответ в виде десятичной дроби (то есть избавиться от корня). С помощью калькулятора найдите √3 и полученное число умножьте на 600: √3 х 600 = 1039,2. Это ваш окончательный ответ.
Реклама
-

1
Найдите площадь треугольника. Формула: Площадь = 1/2 х основание х высота.
- Если вам дан треугольник с основанием 10 и высотой 8, то его площадь = 1/2 х 8 х 10 = 40.
-

2
Найдите площадь квадрата. Чтобы найти площадь квадрата, просто возведите в квадрат длину одной его стороны. Если умножить основание квадрата на его высоту, мы получим тот же ответ, так как основание и высота равны.
- Если сторона квадрата равна 6, то его площадь = 6 х 6 = 36.
-

3
-

4
Найдите площадь трапеции. Формула: Площадь = [(основание1 + основание2) х высота] / 2.
- Например, дана трапеция с основаниями 6 и 8 и высотой 10. Ее площадь = [(6 + 8)•10]/2 = (14 х 10)/2 = 140/2 = 70.
Реклама
-

1
Используйте координаты вершин неправильного многоугольника. Зная координаты вершин, можно определить площадь неправильного многоугольника.
-

2
Сделайте таблицу. Запишите координаты вершин (х,у) (вершины выбирать последовательно в направлении против часовой стрелки). В конце списка еще раз напишите координату первой вершины.
-

3
Умножьте значение координаты «х» первой вершины на значение координаты «у» второй вершины (и так далее). Сложите результаты (в нашем примере сумма равна 82).
-

4
Умножьте значение координаты «у» первый вершины на значение координаты «х» второй вершины (и так далее). Сложите результаты (в нашем примере сумма равна -38).
-

5
Вычтите сумму, полученную в шаге 4, из суммы, полученной в шаге 3. В нашем примере: (82) – (-38) = 120.
-

6
Разделите полученный результат на 2, чтобы найти площадь многоугольника: S=120/2 = 60 (квадратных единиц).
Реклама
Советы
- Если вы записываете координаты вершин в направлении по часовой стрелке, вы получите отрицательную площадь. Таким образом, это можно использовать для описания цикла или последовательности данного набора вершин, формирующих многоугольник.
- Данная формула находит площадь с учетом формы многоугольника. Если многоугольник имеет форму цифры 8, то необходимо из площади с вершинами против часовой стрелки вычесть площадь с вершинами по часовой стрелке.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 439 003 раза.
Была ли эта статья полезной?
![]()
Площадь многоугольника. Друзья! К вашему вниманию пару задачек с многоугольником и вписанной в него окружностью. Существует формула, которой связывается радиус указанной окружности и периметр с площадью такого многоугольника. Вот она:
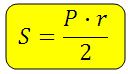
Как выводится эта формула? Просто!
Имеем многоугольник и вписанную окружность. *Рассмотрим вывод на примере пятиугольника. Разобьём его на треугольники (соединим центр окружности и вершины отрезками). Получается, что у каждого треугольника основание является стороной многоугольника, а высоты образованных треугольников равны радиусу вписанной окружности:

Используя формулу площади треугольника можем записать:

Вынесем общие множители:
![]() Уверен, сам принцип вам понятен.
Уверен, сам принцип вам понятен.
*При выводе формулы количество сторон взятого многоугольника не имеет значения. В общем виде вывод формулы выглядел бы так:

*Дополнительная информация!
Известна формула радиуса окружности вписанной в треугольник

Не трудно заметить, что она исходит из полученной нами формулы, посмотрите (a,b,c – это стороны треугольника):


27640. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
 Вычисляем:
Вычисляем:

Ответ: 30
Ещё пара задач с многоугольниками.

27930. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 540. Найдите n.
Если угол между радиусом окружности и стороной многоугольника равен 540, то угол между сторонами многоугольника будет равен 1080. Тут необходимо вспомнить формулу угла правильного многоугольника:

Остаётся подставить в формулу значение угла и вычислить n:

Ответ: 5

27595. Периметры двух подобных многоугольников относятся как 2:7. Площадь меньшего многоугольника равна 28. Найдите площадь большего многоугольника.

Здесь нужно вспомнить о том, что если линейные размеры фигуры увеличивается в k раз, то площадь фигуры увеличивается в k2 раз. *Свойство подобия фигур.
Периметр большего многоугольника больше периметра меньшего в 7/2 раза, значит площадь увеличилась в (7/2)2 раза. Таким образом, площадь большего многоугольника равна:

Ответ: 343
![]()
27639. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.
Посмотреть решение
27641. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Посмотреть решение
27595. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.

Ответ: 50
Всего доброго! Учитесь с удовольствием!
С уважением, Александр.
Периметр фигуры – это общее расстояние вокруг нее, а площадь – это количество поверхности, которую фигура использует или покрывает. Методы расчета периметра и площади отличаются для каждого вида фигуры. Например, хотя вы можете найти площадь прямоугольника, просто умножив его длину на ширину, круг требует более сложных вычислений. Научитесь преобразовывать периметры самых основных фигур в области, и в дальнейшем вы сможете переходить к составным фигурам.
Квадратные Периметры
-
Разделите периметр на четыре
-
Квадрат длина стороны
-
Добавить единицу измерения
Разделите периметр на четыре, чтобы получить длину каждой стороны, так как все четыре стороны квадрата равны. Например, квадрат с периметром 36 дюймов будет иметь стороны размером 9 дюймов каждая, потому что 36 ÷ 4 = 9.
Квадрат длины одной стороны. Для квадрата с 9-дюймовыми сторонами, получится 9 х 9 = 81.
Добавьте правильную единицу измерения к области. Квадрат с периметром 36 дюймов имеет площадь 81 квадратный дюйм.
Периметры прямоугольника
-
Отработка длины основания и высоты
-
Умножить базу на высоту
-
Добавить единицу измерения
Определите длину как основания, так и высоты. Это стороны, которые не параллельны друг другу. Например, скажем, у вас есть прямоугольник с основанием 6 см и высотой 7 см.
Умножьте базу на высоту. Тренируйся 6 х 7 = 42.
Добавьте правильную единицу измерения. В этом примере площадь прямоугольника составляет 42 см квадратных сантиметров.
Периметры треугольника
-
Отработать длину базы
-
Высота тренировки
-
Умножить базу на высоту
-
Разделить на два
-
Добавить единицу измерения
Определите длину основания треугольника. Например, скажем, у вас есть треугольник с основанием 3 фута.
Рассчитайте высоту треугольника. Скажем, у вас есть треугольник с высотой 12 футов.
Умножьте длину основания на длину высоты. Тренируй 3 х 12 = 36.
Разделите на два. Отработать 36 ÷ 2 = 18.
Добавьте правильную единицу измерения. Площадь треугольника составляет 18 квадратных футов.
Окружность окружности
-
Разделить периметр на пи
-
Разделите диаметр на два
-
Умножить радиус
-
Умножить на пи
-
Добавить единицу измерения
Разделите периметр круга, также известный как окружность, на pi (3.14159265), чтобы получить диаметр круга. Например, скажем, у вас есть круг с окружностью 40 дюймов. Отработка 40 ÷ 3.14159265 = 12.732.
Разделите диаметр на два, чтобы получить длину радиуса. Отработать 12, 732 ÷ 2 = 6, 366.
Умножьте радиус на себя. В этом примере получится 6, 366 х 6, 366 = 40, 526.
Умножьте на pi (3.14159265). Отработка 40, 526 х 3, 14159265 = 127, 316.
Добавьте правильную единицу измерения. Площадь круга составляет 127, 316 квадратных дюймов.
