Теория: 05 Площадь поверхности прямоугольных многогранников
Найдите площадь поверхности многогранника, изображенного на рисунке. Все двугранные углы прямые.
Поделим для удобства заданный многогранник на два прямоугольных параллелепипеда, обозначив измерения каждого из них:
Посчитаем площадь поверхности первого параллелепипеда (displaystyle S_1 <small : >)
Для этого вычтем из площади поверхности всего параллелепипеда площадь красной фигуры.
Поскольку измерения параллелепипеда равны (displaystyle 2< small ,>, 1) и (displaystyle 1 < small ,>) а измерения красной фигуры равны (displaystyle color< 1 >) и (displaystyle color< 1> < small ,>) то искомая площадь поверхности равна
(displaystyle S_1=2cdot 1cdot 1+2cdot 2cdot 1+2cdot 1cdot 2-color< 1>cdot color< 1>=2+4+4-color< 1>=9 <small .>)
Посчитаем площадь поверхности второго параллелепипеда (displaystyle S_2 <small : >)
Для этого вычтем из площади поверхности всего параллелепипеда площадь красной фигуры.
Поскольку измерения параллелепипеда равны (displaystyle 1< small ,>, 1) и (displaystyle 1 < small ,>) а измерения красной фигуры равны (displaystyle color< 1 >) и (displaystyle color< 1> < small ,>) то искомая площадь поверхности равна
(displaystyle S_1=2cdot 1cdot 1+2cdot 1cdot 1+2cdot 1cdot 1-color< 1>cdot color< 1>=2+2+2-color< 1>=5 <small .>)
Значит, площадь поверхности (displaystyle S ) заданного многогранника равна
Как найти площадь многогранника прямоугольника
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 2, 3, 1 и двух площадей прямоугольников со сторонами 2, 1:
Почему вы вычитаете только 2 площади прямоугольников? их же там 4,верхняя и боковая еще. Поэтому площадь многогранника будет 15
Обратите внимание, что верхняя и боковая «достраиваются» до целого параллелепипеда из исходной фигуры.
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 3, 5 и двух площадей квадратов со стороной 1:
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5 и площади двух квадратов со стороной 1:
От площади параллелепипеда следует отнять площадь маленького параллелепипеда (5*2+2*1)
Александра, так надо поступать с объемами. С площадями иначе.
Боковая поверхность не изменилась по площади, она просто поменяла форму. А вот от оснований по маленькому квадрату «оттяпали»
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:
Приведем другое решение.
Найдем площадь поверхности многогранника как сумму площадей его граней: горизонтальных, боковых и фронтальных (расположенных спереди и сзади). Рассмотрим горизонтальные грани. Площадь нижней грани равна 5 · 5 = 25. Есть также две верхние грани. Если посмотреть на многогранник сверху, то эти две верхние грани сольются в одну, равную нижней грани. Таким образом, сумма их площадей равна площади нижней грани, то есть 25.
Рассмотрим боковые грани. Площадь левой грани равна 5 · 3 = 15. Есть также две грани справа. Если посмотреть на многогранник справа, то эти две грани сольются в одну, равную левой грани. Таким образом, сумма их площадей равна площади левой грани, то есть 15.
Рассмотрим фронтальные грани. Площадь задней грани равна 5 · 3 = 15. Две передние грани в сумме равны задней грани, таким образом, сумма их площадей тоже равна 15.
Следовательно, площадь поверхности многогранника равна
2 · 25 (горизонтальные грани) + 2 · 15 (боковые грани) + 2 · 15 (фронтальные грани) = 110.
Заметим, что площадь поверхности данного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5. Именно так решена эта задача первым способом.
Нахождение площади прямоугольного параллелепипеда: формула и пример
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:

Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см 2 .
источники:
http://ege.sdamgia.ru/test?theme=148
http://microexcel.ru/ploshhad-pryamougolnogo-parallelepipeda/

{S_{полн} = 2(ab+bc+ac)}
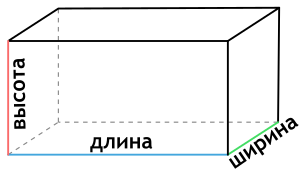
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер – это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота – это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
Как найти площадь поверхности параллелепипеда
На данной странице калькулятор поможет рассчитать площадь поверхности параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
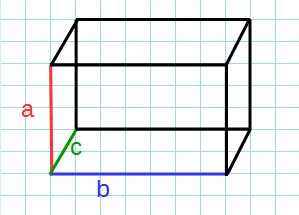
a:
b:
c:
Результат
Ответы:
Формула площади поверхности параллелепипеда через его ребра:
a, b, c – ребра параллелепипеда.
Площадь поверхности прямоугольного параллелепипеда


4.6
Средняя оценка: 4.6
Всего получено оценок: 492.
4.6
Средняя оценка: 4.6
Всего получено оценок: 492.
В 5 классе в курсе математики изучается тема прямоугольного параллелепипеда. Сегодня мы поговорим о формулах для нахождения площади боковой поверхности и площади полной поверхности этой фигуры, которые наиболее часто вызывают затруднения у учеников.

Материал подготовлен совместно с учителем первой категории Камушковой Натальей Владимировной.
Опыт работы учителем математики – 27 лет.
Определения
Параллелепипед – это фигура в пространстве, которая состоит из шести четырехугольников.
Каждый четырехугольник – это грань параллелепипеда. Среди граней различают четыре боковые и два основания. Если в основании фигуры находится прямоугольник, то многогранник называется прямоугольным параллелепипедом.
Стороны граней – это ребра. У параллелепипеда всего 12 ребер.
Параллелепипед имеет 8 вершин, для их обозначения используют заглавные латинские буквы.
Если две грани не имеют общего ребра, то они называются противоположными. Так как каждая грань прямоугольного параллелепипеда – это прямоугольник, у которого противоположные стороны равны, то и противоположные грани прямоугольного параллелепипеда также равны.
Длина ребер определяет основные характеристики прямоугольного параллелепипеда: площадь, периметр, объем.
Примеры таких фигур мы часто встречаем в нашей жизни: кирпич, коробка, системный блок компьютера.
Математическая фигура – прямоугольный параллелепипед активно используется в искусстве, архитектуре и прочих областях.
Различают несколько видов параллелепипедов, с основанием в виде квадрата, параллелограмма или прямоугольника.
Формула для нахождения площади
Для того, чтобы найти площадь боковой поверхности прямоугольного параллелепипеда, необходимо вычислить по отдельности площадь каждой боковой грани, а затем просуммировать получившиеся значения.
$S = ab$;
$S = ac$; где a, b, c – стороны фигуры.
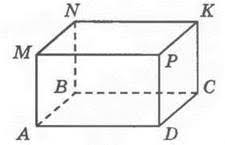
А так как противоположные грани равны, то есть $AMPD = BNKC$, $AMNB = DPKC$, их сумма и будет площадью боковой поверхности многоугольника.
$S= 2(ab + ac)$
Соответственно, чтобы вычислить площадь полной поверхности прямоугольного параллелепипеда необходимо сложить площадь боковой поверхности и две площади основания. В итоге получится формула площади прямоугольного параллелепипеда.
$S = 2(ab + ac) + 2 bc = 2(ab + ac + bc)$
Иногда для уточнения возле знака площади пишут краткое обозначение например, S п.п. – площадь полной поверхности, либо S б.п. – площадь боковой поверхности. Это помогает во время выполнения задания не перепутать нужные данные.
Пример задания
Найти площадь полной поверхности прямоугольного параллелепипеда, если длина и ширина основания 4 см и 3 см соответственно, а высота равна 2 см.
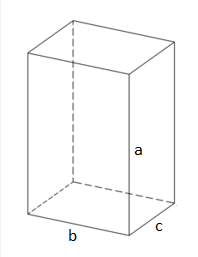
Решение:
S п.п. = 2(ab + ac + bc)
S п.п. = 2(4*3 + 4*2 + 3*2) = 52 см2
Таким образом, S п.п. = 52 см2.
Для площади поверхности прямоугольного параллелепипеда используют те же единицы измерения, в которых были приведены длины ребер. Если длины ребер прямоугольного параллелепипеда даны в разных единицах измерения, то их нужно перевести в одинаковые.

Что мы узнали?
Мы познакомились с элементами прямоугольного параллелепипеда: грани, ребра, основание. А также ознакомились с формулами для нахождения площади его боковой и полной поверхности, которые можно использовать для решения заданий.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Марина Яговцева
8/10
-

Розочка Ангелиночка
10/10
-

Слава Сироткин
10/10
-

Тома Зимина
7/10
-

Artem Sevastanov
10/10
-

Влад Чибиряев
10/10
-

Александр Селезнев
10/10
-

Акрам Сафарбеков
10/10
-

Вера Машковцева
10/10
-

Александр Семёнов
9/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 492.
А какая ваша оценка?
Параллелепипед — это многогранник, который представляет собой частный вид прямоугольной шестигранной призмы. В основании параллелепипеда лежит прямоугольник или равносильный ему четырехугольник, а в качестве боковых поверхностей выступают параллелограммы. Как и любая призматическая фигура, параллелепипед широко распространен в реальной жизни, но в большинстве случаев реальный многогранник принимает форму прямоугольного параллелепипеда.
Геометрия параллелепипеда
Прямоугольный параллелепипед представляет собой два одинаковых прямоугольника, лежащие в параллельных плоскостях и четыре соединяющих их прямоугольника, которые образуют боковую поверхность фигуры. В общем случае параллелепипед представляет собой частный случай прямой четырехугольной призмы. Параллелепипед — наиболее распространенная в реальной жизни фигура. Именно форму данного многогранника имеют такие объекты как дома, комнаты, кирпичи, картонные коробки, блоки компьютеров, упаковки молока, спичечные коробки и многое другое.
Реальный мир состоит их различных геометрических фигур, поэтому вам может понадобиться калькулятор, который мгновенно посчитает площадь поверхности объекта, имеющего форму прямоугольного параллелепипеда, будь то корпусная мебель, кладовка или системный блок стационарного компьютера.
Площадь поверхности параллелепипеда
Площадь полной поверхности такой призмы определяется как сумма площадей всех граней. Параллелепипед представляет собой шестигранник, каждая пара граней которого равны между собой. Это означает, что каждая грань параллелепипеда имеет свою конгруэнтную пару. Таким образом, площадь поверхности данной призматической фигуры выражается как двойная сумма площадей каждой грани.
S = 2 (Sa + Sb + Sc)
Так как каждая грань параллелепипеда представляет собой обычный прямоугольник, то площадь одной грани определяется как произведение сторон многоугольника. Если призматическая фигура имеет стороны a, b и c, то площадь ее полной поверхности будет равна:
S = 2 (ab + bc + ac)
Для более простого понимания можем представить формулу через длину, ширину и высоту параллелепипеда. В этом случае в формуле будет лишь небольшое изменение:
S = 2 (ab + bh + ah)
Таким образом, для определения площади полной поверхности призматической фигуры вам понадобится узнать три ее параметра. Введите эти данные в форму онлайн-калькулятора и вы получите мгновенный результат. Кроме того, калькулятор сразу подсчитает длину диагонали многогранника. Расчет площади поверхности призматической фигуры может понадобиться вам во многих ситуациях.
Примеры из жизни
Покраска стен
Допустим, вы хотите покрасить стены, пол и потолок кухни белой краской. Вам необходимо купить достаточное количество краски для обработки выбранного помещения. Зная, что расход масляной краски на 1 квадратный метр поверхности составляет приблизительно 200 грамм, вы можете определить, сколько материала вам понадобится для работы. Пусть высота кухонного помещения составляет 3 м, ширина 2 м, а длина — 5 м. Введите эти данные в онлайн-калькулятор и вы получите результат в виде:
S = 62
Таким образом, вам понадобится покрасить 62 квадратных метров поверхности. Для этого вам потребуется купить 12,4 кг масляной краски или 5 банок краски по 2,8 кг.
Производство
Допустим, вы работаете на производстве и покрываете стальной квадратный профиль защитным покрытием, окуная детали в ванную с раствором. Для правильного расчета параметров покраски вам необходимо знать площадь поверхности одного стального профиля, который имеет форму параллелепипеда. Стандартный квадратный профиль имеет размеры: длина 6 м, сторона а = 80 мм, сторона b = 80 мм. Для правильного расчета вам необходимо подставить все размеры в одних единицах измерения, к примеру, в сантиметрах. В этом случае вбейте в онлайн-калькулятор три стороны параллелепипеда, которые равны 600, 8 и 8. Вы получите результат в виде:
S = 19 328
Таким образом, полная площадь поверхности стального профиля составляет 19 328 квадратных сантиметров или 1,9828 квадратных метра. Зная площадь поверхности одного профиля, вы легко сможете определить параметры покраски деталей защитным покрытием.
Заключение
Большое количество реальных объектов имеет форму параллелепипеда: это и кирпичи, и комнаты, и здания, и детали машин, и многое другое. Расчет площади данного многогранника может понадобиться в самых неожиданных ситуациях, как-то житейские проблемы или профессиональные расчеты. Наш онлайн-калькулятор поможет вам быстро определить объемы и площади поверхностей любых правильных геометрических фигур.
