В данной статье речь пойдёт о том, как выразить площадь многоугольника, в который можно вписать окружность, через радиус этой окружности. Сразу стоит отметить, что не во всякий многоугольник можно вписать окружность. Однако, если это возможно, то формула, по которой вычисляется площадь такого многоугольника, становится очень простой. Дочитайте эту статью до конца или посмотрите прилагающийся видеоурок, и вы узнаете, как же выразить площадь многоугольника через радиус вписанной в него окружности.
Формула площади многоугольника через радиус вписанной окружности
Нарисуем многоугольник A1A2A3A4A5, не обязательно правильный, но такой, в который можно вписать окружность. Напомню, что вписанной называется окружность, которая касается всех сторон многоугольника. На рисунке это зелёная окружность с центром в точке O:
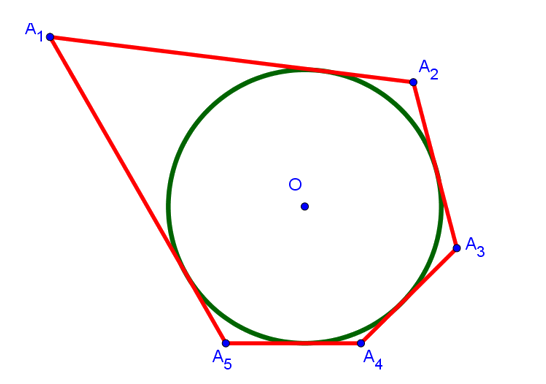
Мы взяли здесь для примера 5-угольник. Но на самом деле это не имеет существенного значения, поскольку дальнейшее доказательство справедливо и для 6-угольника и для 8-угольника и вообще для любого сколь угодно «угольника».
Если соединить центр вписанной окружности со всеми вершинами многоугольника, то он разобьётся на столько треугольников, сколько вершин в данном многоугольнике. В нашем случае: на 5 треугольников. Если же соединить точку O со всеми точками касания вписанной окружности со сторонами многоугольника, то получится 5 отрезков (на рисунке снизу это отрезки OH1, OH2, OH3, OH4 и OH5), которые равны радиусу окружности и перпендикулярны сторонам многоугольника, к которым они проведены. Последнее справедливо, поскольку радиус, проведенный в точку касания, перпендикулярен касательной:
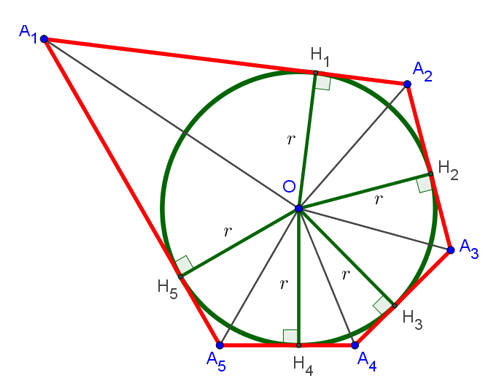
Как же найти площадь нашего описанного многоугольника? Ответ прост. Нужно сложить площади всех полученных в результате разбиения треугольников:
![]()
Рассмотрим, чему равна площадь треугольника ![]() . На рисунке снизу он выделен жёлтым цветом:
. На рисунке снизу он выделен жёлтым цветом:
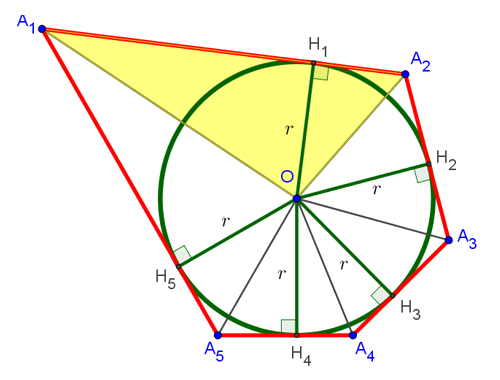
Она равна половине произведения основания A1A2 на высоту OH1, проведённую к этому основанию. Но, как мы уже выяснили, эта высота равна радиусу вписанной окружности. То есть формула площади треугольника принимает вид: ![]() , где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:
, где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:
![]()
![]()
Видно, что во всех слагаемых этой суммы ест общий множитель ![]() , который можно вынести за скобки. В результате получится вот такое выражение:
, который можно вынести за скобки. В результате получится вот такое выражение:
![]()
То есть в скобках осталась просто сумма всех сторон многоугольника, то есть его периметр P. Чаще всего в этой формуле выражение ![]() заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:
заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:
![]()
То есть площадь многоугольника, в который вписана окружность известного радиуса, равна произведению этого радиуса на полупериметр многоугольника. Это и есть тот результат, в которому мы стремились.
Отметит напоследок, что в треугольник, который является частным случаем многоугольника, всегда можно вписать окружность. Поэтому для треугольника эту формулу можно применять всегда. Для остальных многоугольников, с количеством сторон большим 3, сперва нужно убедиться, что в них можно вписать окружность. Если это так, можно смело использовать эту простую формулу и находить по ней площадь этого многоугольника.
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич
Площадь правильного многоугольника
Онлайн калькулятор – площадь правильного многоугольника
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Правильный многоугольник так же называют правильным n-угольником, где n – это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).
В любой правильный многоугольник можно вписать окружность. Такая окружность называется вписанной окружностью.
Около любого правильного многоугольника можно описать окружность.
Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.
Формула площади правильного многоугольника
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Правильный многоугольник так же называют правильным n-угольником , где n – это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).
В любой правильный многоугольник можно вписать окружность. Такая окружность называется вписанной окружностью .
Около любого правильного многоугольника можно описать окружность.
Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.
Площади многоугольников
Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник. За единицу измерения площади принимают площадь квадрата со стороной (1) см, (1) мм и т.д. (единичный квадрат). Тогда площадь будет измеряться в см (^2) , мм (^2) соответственно.
Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.
Свойства площади
1. Площадь любого многоугольника — величина положительная.
2. Равные многоугольники имеют равные площади.
3. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
4. Площадь квадрата со стороной (a) равна (a^2) .
Теорема: площадь прямоугольника
Площадь прямоугольника со сторонами (a) и (b) равна (S=ab) .
Доказательство
Достроим прямоугольник (ABCD) до квадрата со стороной (a+b) , как показано на рисунке:
Данный квадрат состоит из прямоугольника (ABCD) , еще одного равного ему прямоугольника и двух квадратов со сторонами (a) и (b) . Таким образом,
Определение
Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота (BK) падает на сторону (AD) , а высота (BH) — на продолжение стороны (CD) :
Теорема: площадь параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Проведем перпендикуляры (AB’) и (DC’) , как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма (ABCD) .
Тогда (AB’C’D) – прямоугольник, следовательно, (S_=AB’cdot AD) .
Заметим, что прямоугольные треугольники (ABB’) и (DCC’) равны. Таким образом,
Определение
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
Пусть (S) – площадь треугольника (ABC) . Примем сторону (AB) за основание треугольника и проведём высоту (CH) . Докажем, что [S = dfrac<1><2>ABcdot CH.] Достроим треугольник (ABC) до параллелограмма (ABDC) так, как показано на рисунке:
Треугольники (ABC) и (DCB) равны по трем сторонам ( (BC) – их общая сторона, (AB = CD) и (AC = BD) как противоположные стороны параллелограмма (ABDC) ), поэтому их площади равны. Следовательно, площадь (S) треугольника (ABC) равна половине площади параллелограмма (ABDC) , то есть (S = dfrac<1><2>ABcdot CH) .
Теорема
Если два треугольника (triangle ABC) и (triangle A_1B_1C_1) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.
Теорема
Если два треугольника (triangle ABC) и (triangle A_2B_2C_2) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
Доказательство
Пусть (angle A=angle A_2) . Совместим эти углы так, как показано на рисунке (точка (A) совместилась с точкой (A_2) ):
Проведем высоты (BH) и (C_2K) .
Треугольники (AB_2C_2) и (ABC_2) имеют одинаковую высоту (C_2K) , следовательно: [dfrac>>=dfrac]
Треугольники (ABC_2) и (ABC) имеют одинаковую высоту (BH) , следовательно: [dfrac>>=dfrac]
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Пусть (p) – полупериметр треугольника, (a) , (b) , (c) – длины его сторон, тогда его площадь равна [S_<triangle>=sqrt]
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Рассмотрим четырехугольник (ABCD) . Обозначим (AO=a, CO=b, BO=x, DO=y) :
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:
(begin S_=frac12ax+frac12xb+frac12by+frac12ay=frac12(ax+xb+by+ay)=\ frac12((a+b)x+(a+b)y)=frac12(a+b)(x+y)end)
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: [S_<text<ромб>>=dfrac12 d_1cdot d_2]
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.
Теорема: площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство
Рассмотрим трапецию (ABCD) с основаниями (BC) и (AD) . Проведем (CD’parallel AB) , как показано на рисунке:
Тогда (ABCD’) – параллелограмм.
Проведем также (BH’perp AD, CHperp AD) ( (BH’=CH) – высоты трапеции).
Тогда (S_=BH’cdot AD’=BH’cdot BC, quad S_=dfrac12CHcdot D’D)
Т.к. трапеция состоит из параллелограмма (ABCD’) и треугольника (CDD’) , то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:
[S_=S_+S_=BH’cdot BC+dfrac12CHcdot D’D=dfrac12CHleft(2BC+D’Dright)=] [=dfrac12 CHleft(BC+AD’+D’Dright)=dfrac12 CHleft(BC+ADright)]
[spoiler title=”источники:”]
http://calcsbox.com/post/formula-plosadi-pravilnogo-mnogougolnika.html
http://shkolkovo.net/theory/56
[/spoiler]
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Длина окружности и площадь круга
- Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Пусть 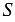 – площадь правильного
– площадь правильного 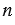 -угольника,
-угольника, 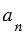 – его сторона,
– его сторона, 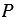 – периметр, а
– периметр, а 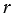 и
и 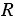 – радиусы соответственно вписанной и описанной окружностей.
– радиусы соответственно вписанной и описанной окружностей.
Докажем, что 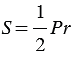 .
.
Доказательство:
Соединим центр О данного многоугольника с вершинами А1, А2, …, Аn.
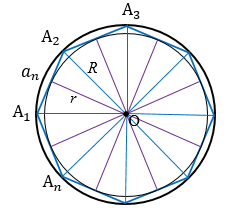
Многоугольник разобьется на 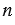 равных треугольников, т.е.
равных треугольников, т.е. 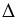 А1ОА2 =
А1ОА2 = 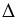 А2ОА3 = … =
А2ОА3 = … = 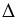 А1ОАn по трем сторонам (ОА1 = ОА2 = … = ОАn, как радиусы описанной окружности и А1А2 = А2А3 = … = АnА1 =
А1ОАn по трем сторонам (ОА1 = ОА2 = … = ОАn, как радиусы описанной окружности и А1А2 = А2А3 = … = АnА1 = 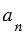 , как стороны правильного многоугольника). Равные треугольники имеют равные площади, поэтому площадь каждого из полученных треугольников будет равна
, как стороны правильного многоугольника). Равные треугольники имеют равные площади, поэтому площадь каждого из полученных треугольников будет равна 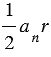 . Следовательно,
. Следовательно, 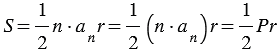 (свойство площадей многоугольников). Что и требовалось доказать.
(свойство площадей многоугольников). Что и требовалось доказать.
Выведем формулы:
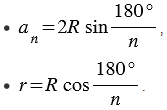
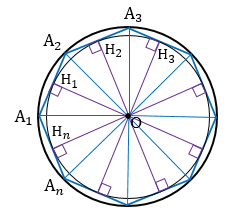
В прямоугольном 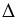 А1Н1О:
А1Н1О:
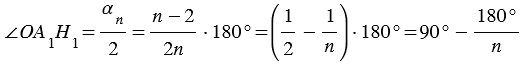 ,
,
где 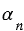 – угол правильного многоугольника А1А2А3…Аn.
– угол правильного многоугольника А1А2А3…Аn.
Н1 – середина А1А2 (смотри следствие из теоремы об окружности, вписанной в правильный многоугольник), следовательно, 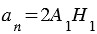 , при этом
, при этом 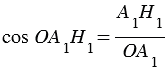 , откуда
, откуда 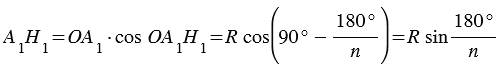 (смотри формулы приведения), следовательно,
(смотри формулы приведения), следовательно, 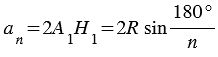 .
.
В прямоугольном 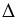 А1Н1О:
А1Н1О:
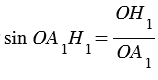 , откуда
, откуда 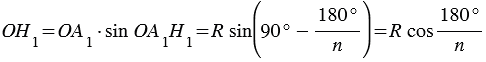 (смотри формулы приведения), следовательно,
(смотри формулы приведения), следовательно, 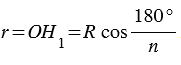 .
.
Примечание:
Если в формулу 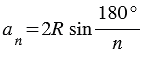 подставить значения
подставить значения 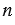 = 3, 4 и 6, получим выражения для сторон правильного треугольника, квадрата и правильного шестиугольника:
= 3, 4 и 6, получим выражения для сторон правильного треугольника, квадрата и правильного шестиугольника:
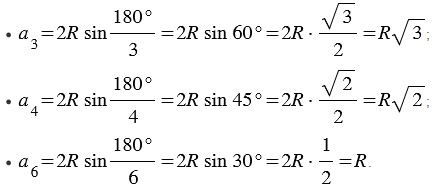
Советуем посмотреть:
Правильный многоугольник
Окружность, описанная около правильного многоугольника
Окружность, вписанная в правильный многоугольник
Построение правильных многоугольников
Длина окружности
Площадь круга
Площадь кругового сектора
Длина окружности и площадь круга
Правило встречается в следующих упражнениях:
7 класс
Задание 1088,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1095,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1130,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1131,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1133,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1205,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1239,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Найдём площадь правильного многоугольника через радиусы вписанной и описанной окружностей и через его сторону.
Любой правильный многоугольник вписан в окружность и описан около окружности. Центры вписанной и описанной окружностей совпадают и называются центром правильного многоугольника.
 Соединив центр правильного n-угольника
Соединив центр правильного n-угольника
![]()
со всеми его вершинами, получим n равнобедренных треугольников.
Основание каждого такого треугольника равно стороне многоугольника, боковые стороны равны радиусу описанной около многоугольника окружности угол при вершине — центральному углу правильного многоугольника
![]()
![]()
![]()
Так как площадь треугольника равна половине произведения его сторон на синус угла между ними,
![]()
Отсюда
![]()
Поскольку многоугольник состоит из n таких треугольников, формула площади правильного многоугольника через радиус описанной окружности:
![]()
 Проведём в треугольнике A1OA2 высоту OF. Её длина равна радиусу вписанной в правильный n-угольник окружности:
Проведём в треугольнике A1OA2 высоту OF. Её длина равна радиусу вписанной в правильный n-угольник окружности:
![]()
По свойству равнобедренного треугольника OF является также его биссектрисой и медианой:
![]()
![]()
Из прямоугольного треугольника A1OF по определению тангенса
![]()
откуда
![]()
Так как площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне,
![]()
![]()
Площадь
![]()
равна сумме n таких площадей.
Таким образом, формула площади правильного многоугольника через радиус вписанной окружности:
![]()
Из треугольника A1OF
![]()
Следовательно,
![]()
Поскольку многоугольник состоит из n равных треугольников, формула площади правильного многоугольника через его сторону:
![]()
Содержание:
Площади поверхностей геометрических тел:
Под площадью поверхности многогранника мы понимаем сумму площадей всех его граней. Как же определить площадь поверхности тела, не являющегося многогранником? На практике это делают так. Разбивают поверхность на такие части, которые уже мало отличаются от плоских. Тогда находят площади этих частей, как будто они являются плоскими. Сумма полученных площадей является приближенной площадью поверхности. Например, площадь крыши здания определяется как сумма площадей кусков листового металла. Еще лучше это видно на примере Земли. Приблизительно она имеет форму шара. Но площади небольших ее участков измеряют так, как будто эти участки являются плоскими. Более того, под площадью поверхности тела будем понимать предел площадей полных поверхностей описанных около него многогранников. При этом должно выполняться условие, при котором все точки поверхности этих многогранников становятся сколь угодно близкими к поверхности данного тела. Для конкретных тел вращения понятие описанного многогранника будет уточнено.
Понятие площади поверхности
Рассмотрим периметры 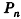
Применим данные соотношения к обоснованию формулы для площади боковой поверхности цилиндра.
При вычислении объема цилиндра были использованы правильные вписанные в него призмы. Найдем при помощи в чем-то аналогичных рассуждений площадь боковой поверхности цилиндра.
Опишем около данного цилиндра радиуса R и высоты h правильную n-угольную призму (рис. 220).
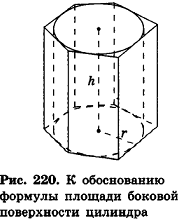
Площадь боковой поверхности призмы равна
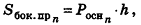
где 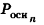 — периметр основания призмы.
— периметр основания призмы.
При неограниченном возрастании n получим:
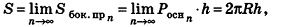
так как периметры оснований призмы стремятся к длине окружности основания цилиндра, то есть к 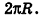
Учитывая, что сумма площадей двух оснований призмы стремится к 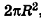 , получаем, что площадь полной поверхности цилиндра равна
, получаем, что площадь полной поверхности цилиндра равна 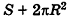 . Но сумма площадей двух оснований цилиндра равна
. Но сумма площадей двух оснований цилиндра равна 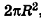 . Поэтому найденную величину S принимают за площадь боковой поверхности цилиндра.
. Поэтому найденную величину S принимают за площадь боковой поверхности цилиндра.
Итак, площадь боковой поверхности цилиндра вычисляется по формуле
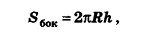
где R — радиус цилиндра, h — его высота.
Заметим, что эта формула аналогична соответствующей формуле площади боковой поверхности прямой призмы 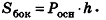
За площадь полной поверхности цилиндра принимается сумма площадей боковой поверхности и двух оснований:
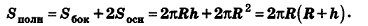
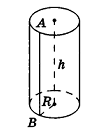
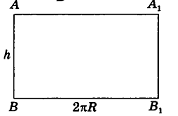
Если боковую поверхность цилиндра радиуса R и высоты h разрезать по образующей АВ и развернуть на плоскость, то в результате получим прямоугольник 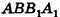 который называется разверткой боковой поверхности цилиндра (рис. 221).
который называется разверткой боковой поверхности цилиндра (рис. 221).
Очевидно, что сторона 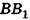 этого прямоугольника есть развертка окружности основания цилиндра, следовательно,
этого прямоугольника есть развертка окружности основания цилиндра, следовательно, 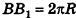 . Сторона АВ равна образующей цилиндра, то есть АВ = h. Значит, площадь развертки боковой поверхности цилиндра равна
. Сторона АВ равна образующей цилиндра, то есть АВ = h. Значит, площадь развертки боковой поверхности цилиндра равна 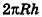 . Таким образом, площадь боковой поверхности цилиндра равна площади ее развертки.
. Таким образом, площадь боковой поверхности цилиндра равна площади ее развертки.

Пример:
Параллельно оси цилиндра на расстоянии d от нее проведена плоскость, отсекающая от основания дугу 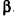 . Диагональ полученного сечения наклонена к плоскости основания под углом а. Определите площадь боковой поверхности цилиндра.
. Диагональ полученного сечения наклонена к плоскости основания под углом а. Определите площадь боковой поверхности цилиндра.
Решение:
Пусть дан цилиндр, в основаниях которого лежат равные круги с центрами 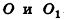
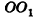 — ось цилиндра. Рассмотрим плоскость, параллельную
— ось цилиндра. Рассмотрим плоскость, параллельную 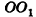 . Сечение цилиндра данной плоскостью представляет собой прямоугольник
. Сечение цилиндра данной плоскостью представляет собой прямоугольник 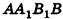 (рис. 222).
(рис. 222).
Пусть хорда АВ отсекает от окружности основания дугу 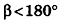 . Тогда, по определению,
. Тогда, по определению, 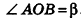 . Так как образующие цилиндра перпендикулярны основаниям,
. Так как образующие цилиндра перпендикулярны основаниям, 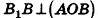 . Значит, АВ — проекция
. Значит, АВ — проекция 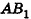 на плоскость АОВ, тогда угол между
на плоскость АОВ, тогда угол между 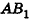 и плоскостью АОВ равен углу
и плоскостью АОВ равен углу 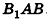 . По условию
. По условию 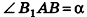 .
.
В равнобедренном треугольнике 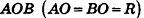 проведем медиану ОК. Тогда O
проведем медиану ОК. Тогда O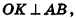
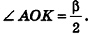 Так как
Так как 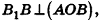 то
то 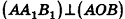 по признаку перпендикулярных плоскостей. Но тогда
по признаку перпендикулярных плоскостей. Но тогда 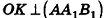 по свойству перпендикулярных плоскостей. Значит, ОК — расстояние между точкой О и плоскостью
по свойству перпендикулярных плоскостей. Значит, ОК — расстояние между точкой О и плоскостью 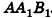 . Учитывая, что
. Учитывая, что 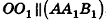 , по определению расстояния между параллельными прямой и плоскостью получаем, что ОК равно расстоянию между
, по определению расстояния между параллельными прямой и плоскостью получаем, что ОК равно расстоянию между 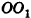 и плоскостью
и плоскостью 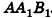 . По условию OK = d. Из прямоугольного треугольника АКО
. По условию OK = d. Из прямоугольного треугольника АКО
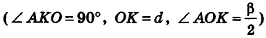 имеем:
имеем: 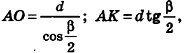
откуда 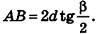 Из прямоугольного треугольника
Из прямоугольного треугольника 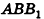
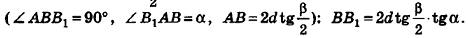
Итак, 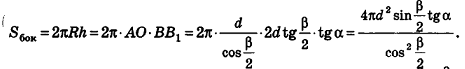
В случае, когда 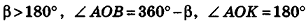
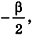
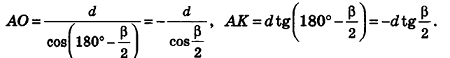
Аналогично предыдущему, и в этом случае получаем тот же результат для площади боковой поверхности.
Ответ: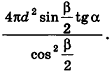
Площадь поверхности конуса и усеченного конуса
Связь между цилиндрами и призмами полностью аналогична связи между конусами и пирамидами. В частности, это касается формул для площадей их боковых поверхностей.
Опишем около данного конуса с радиусом основания R и образующей I правильную л-угольную пирамиду (рис. 223). Площадь ее боковой поверхности равна
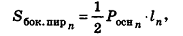
где 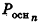 — периметр основания пирамиды,
— периметр основания пирамиды, 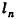 — апофема.
— апофема.
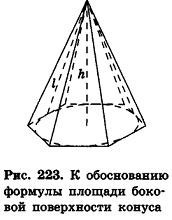
При неограниченном возрастании n получим:
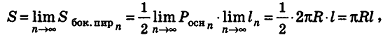
так как периметры оснований пирамиды стремятся к длине окружности основания конуса, а апофемы 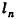 равны I.
равны I.
Учитывая, что площадь основания пирамиды стремится к 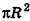 , получаем, что площадь полной поверхности конуса равна
, получаем, что площадь полной поверхности конуса равна 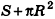 . Но площадь основания конуса равна
. Но площадь основания конуса равна 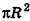 . Поэтому найденную величину S принимают за площадь боковой поверхности конуса. Итак, площадь боковой поверхности конуса вычисляется по формуле
. Поэтому найденную величину S принимают за площадь боковой поверхности конуса. Итак, площадь боковой поверхности конуса вычисляется по формуле
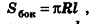
где R — радиус основания, I — образующая.
За площадь полной поверхности конуса принимается сумма площадей его основания и боковой поверхности:
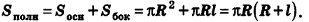
Если боковую поверхность конуса разрезать по образующей РА и развернуть на плоскость, то в результате получим круговой сектор 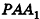 который называется разверткой боковой поверхности конуса (рис. 224).
который называется разверткой боковой поверхности конуса (рис. 224).
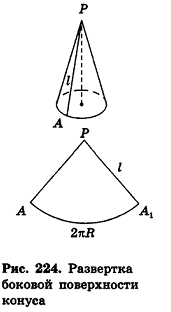
Очевидно, что радиус сектора развертки равен образующей конуса I, а длина дуги 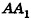 — длине окружности основания конуса, то есть
— длине окружности основания конуса, то есть 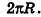 . Учитывая, что площадь соответствующего круга равна
. Учитывая, что площадь соответствующего круга равна 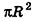 , получаем:
, получаем: 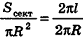 , значит,
, значит, 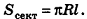 Таким образом, площадь боковой поверхности конуса равна площади ее развертки.
Таким образом, площадь боковой поверхности конуса равна площади ее развертки.
Учитывая формулу для площади боковой поверхности конуса, нетрудно найти площадь боковой поверхности усеченного конуса.
Рассмотрим усеченный конус, полученный при пересечении конуса с вершиной Р некоторой секущей плоскостью (рис. 225).
Пусть 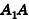 — образующая усеченного конуса
— образующая усеченного конуса 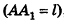 точки
точки 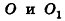 — центры большего и меньшего оснований с радиусами R и г соответственно. Тогда площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей двух конусов:
— центры большего и меньшего оснований с радиусами R и г соответственно. Тогда площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей двух конусов:
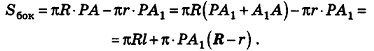
Из подобия треугольников 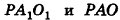
следует, что 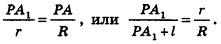
Тогда получаем 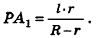
Таким образом, 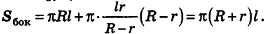
Итак, мы получили формулу для вычисления площади боковой поверхности усеченного конуса: 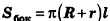 , где R и г — радиусы оснований усеченного конуса, I — его образующая.
, где R и г — радиусы оснований усеченного конуса, I — его образующая.
Отсюда ясно, что площадь полной поверхности усеченного конуса равна 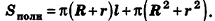
Такой же результат можно было бы получить, если найти площадь развертки боковой поверхности усеченного конуса или использовать правильные усеченные пирамиды, описанные около него. Попробуйте дать соответствующие определения и провести необходимые рассуждения самостоятельно.
Связь между площадями поверхностей и объемами
При рассмотрении объемов и площадей поверхностей цилиндра и конуса мы видели, что существует тесная взаимосвязь между этими фигурами и призмами и пирамидами соответственно. Оказывается, что и сфера (шар), вписанная в многогранник, связана с величиной его объема.
Определение:
Сфера (шар) называется вписанной в выпуклый многогранник, если она касается каждой его грани.
При этом многогранник называется описанным около данной сферы (рис. 226).
Рассмотрим, например, сферу, вписанную в тетраэдр (рис. 227).
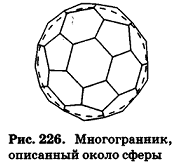
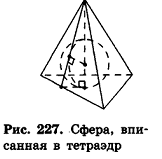
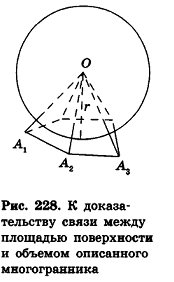
Плоскости, содержащие грани тетраэдра, являются касательными к вписанной сфере, а точки касания лежат в гранях тетраэдра. Заметим, что по доказанному в п. 14.2 радиусы вписанной сферы, проведенные в точку касания с поверхностью многогранника, перпендикулярны плоскостям граней этого многогранника.
Для описанных многоугольников на плоскости было доказано, что их площадь равна произведению полупериметра на радиус вписанной окружности. Аналогичное свойство связывает объем описанного многогранника и площадь его поверхности.
Теорема (о связи площади поверхности и объема описанного многогранника)
Объем описанного многогранника вычисляется по формуле
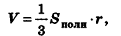
где 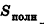 — площадь полной поверхности многогранника, г — радиус вписанной сферы.
— площадь полной поверхности многогранника, г — радиус вписанной сферы.
Доказательство:
Соединим центр вписанной сферы О со всеми вершинами многогранника  (рис. 228). Получим n пирамид, основаниями которых являются грани многогранника, вершины совпадают с точкой О, высоты равны г. Тогда объем многогранника, по аксиоме, равен сумме объемов этих пирамид. Используя формулу объема пирамиды, найдем объем данного многогранника:
(рис. 228). Получим n пирамид, основаниями которых являются грани многогранника, вершины совпадают с точкой О, высоты равны г. Тогда объем многогранника, по аксиоме, равен сумме объемов этих пирамид. Используя формулу объема пирамиды, найдем объем данного многогранника:
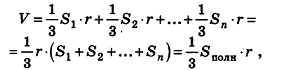
где 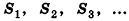 – площади граней многогранника.
– площади граней многогранника.
Теорема доказана.
Оказывается, что в любой тетраэдр можно вписать сферу, и только одну. Но не каждый выпуклый многогранник обладает этим свойством.
Рассматривают также сферы, описанные около многогранника.
Определение:
Сфера называется описанной около многогранника, если все его вершины лежат на сфере.
При этом многогранник называется вписанным в сферу (рис. 229).
Также считается, что соответствующий шар описан около многогранника.
Около любого тетраэдра можно описать единственную сферу, но не каждый многогранник обладает соответствующим свойством.
Площадь сферы
Применим полученную связь для объемов и площадей поверхностей описанных многогранников к выводу формулы площади сферы.
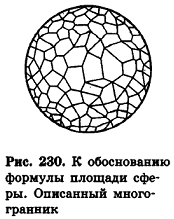
Опишем около сферы радиуса R выпуклый многогранник (рис. 230).
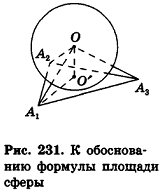
Пусть S’ — площадь полной поверхности данного многогранника, а любые две точки одной грани удалены друг от друга меньше чем на е. Тогда объем многогранника равен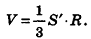 . Рассмотрим расстояние от центра сферы О до любой вершины многогранника, например А1 (рис. 231).
. Рассмотрим расстояние от центра сферы О до любой вершины многогранника, например А1 (рис. 231).
По неравенству треугольника 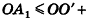
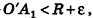 где О’ — точка касания. Отсюда следует, что все вершины данного многогранника лежат внутри шара с центром О и радиусом
где О’ — точка касания. Отсюда следует, что все вершины данного многогранника лежат внутри шара с центром О и радиусом 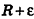 .
.
Итак, объем V данного многогранника больше объема шара радиуса R и меньше объема шара радиуса 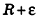 , то есть
, то есть 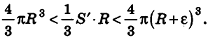
Отсюда получаем 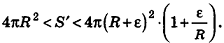
Если неограниченно уменьшать размеры граней многогранника, то есть при е, стремящемся к нулю, левая и правая части последнего неравенства будут стремиться к 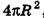 , а многогранник все плотнее примыкать к сфере. Поэтому полученную величину для предела S’ принимают за площадь сферы.
, а многогранник все плотнее примыкать к сфере. Поэтому полученную величину для предела S’ принимают за площадь сферы.
Итак, площадь сферы радиуса R вычисляется по формуле 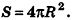
Доказанная формула означает, что площадь сферы равна четырем площадям ее большого круга (рис. 232).
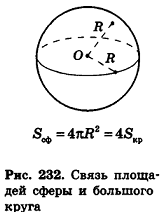
Исходя из аналогичных рассуждений, можно получить формулу для площади сферической части шарового сегмента с высотой Н:
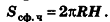
Оказывается, что эта формула справедлива и для площади сферической поверхности шарового слоя (пояса):
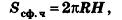
где Н — высота слоя (пояса).
Справочный материал
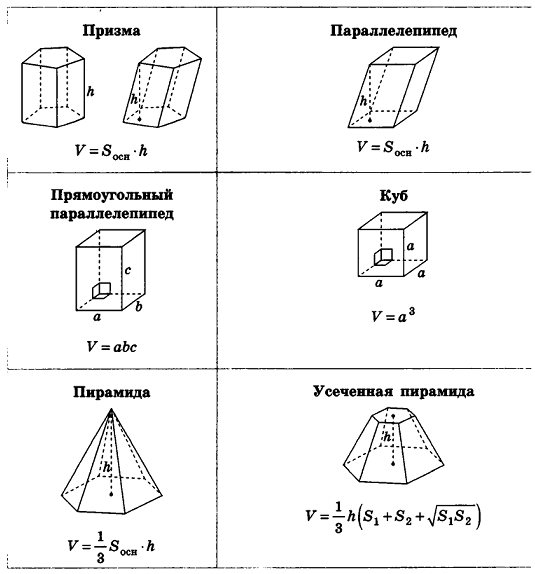
Формулы объемов и площадей поверхностей геометрических тел
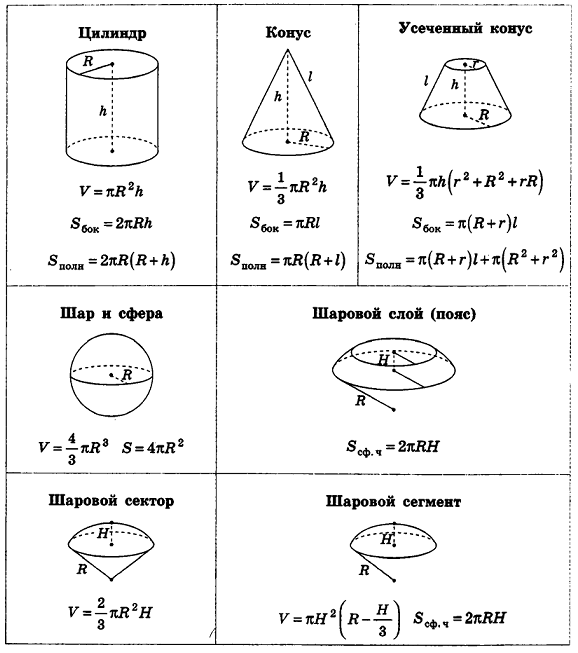
Историческая справка
Многие формулы для вычисления объемов многогранников были известны уже в Древнем Египте. В так называемом Московском папирусе, созданном около 4000 лет назад, вероятно, впервые в истории вычисляется объем усеченной пирамиды. Но четкие доказательства большинства формул для объемов появились позднее, в работах древнегреческих ученых.
Так, доказательства формул для объемов конуса и пирамиды связаны с именами Демокрита из Абдеры (ок. 460-370 гг. до н. э.) и Евдокса Книдского (ок. 408-355 гг. до н. э.). На основании их идей выдающийся математик и механик Архимед (287-212 гг. до н. э.) вычислил объем шара, нашел формулы для площадей поверхностей цилиндра, конуса, сферьГг
Дальнейшее развитие методы, предложенные Архимедом, получили благодаря трудам средневекового итальянского монаха и математика Бонавентуры Кавальери (1598-1647). В своей книге «Геометрия неделимых» он сформулировал принцип сравнения объемов, при котором используются площади сечений. Его рассуждения стали основой интегральных методов вычисления объемов, разработанных Исааком Ньютоном (1642 (1643)-1727) и Готфридом Вильгельмом фон Лейбницем (1646-1716). Во многих учебниках по геометрии объем пирамиды находится с помощью * чертовой лестницы» — варианта древнегреческого метода вычерпывания, предложенного французским математиком А. М. Лежандром (1752-1833).


На II Международном конгрессе математиков, который состоялся в 1900 году в Париже, Давид Гильберт сформулировал, в частности, такую проблему: верно ли, что любые два равновеликих многогранника являются равносоставленными? Уже через год отрицательный ответ на этот вопрос был обоснован учеником Гильберта Максом Деном (1878-1952). Другое доказательство этого факта предложил в 1903 году известный геометр В. Ф. Каган, который в начале XX века вел плодотворную научную и просветительскую деятельность в Одессе. В частности, из работ Дена и Кагана следует, что доказательство формулы объема пирамиды невозможно без применения пределов.
Весомый вклад в развитие теории площадей поверхностей внесли немецкие математики XIX века. Так, в 1890 году Карл Герман Аман-дус Шварц (1843-1921) построил пример последовательности многогранных поверхностей, вписанных в боковую поверхность цилиндра («сапог Шварца»). Уменьшение их граней не приводит к приближению суммы площадей этих граней к площади боковой поверхности цилиндра. Это стало толчком к созданию выдающимся немецким математиком и физиком Германом Минков-ским (1864-1909) современной теории площадей поверхностей, в которой последние связаны с объемом слоя около данной поверхности.
Учитывая огромный вклад Архимеда в развитие математики, в частности теории объемов и площадей поверхностей, именно его изобразили на Филдсовской медали — самой почетной в мире награде для молодых математиков. В 1990 году ею был награжден Владимир Дрин-фельд (род. в 1954 г.), который учился и некоторое время работал в Харькове. Вот так юные таланты, успешно изучающие геометрию в школе, становятся в дальнейшем всемирно известными учеными.




Уравнения фигур в пространстве
Напомним, что уравнением фигуры F на плоскости называется уравнение, которому удовлетворяют координаты любой точки фигуры F и не удовлетворяют координаты ни одной точки, не принадлежащей фигуре F. Так же определяют и уравнение фигуры в пространстве; но, в отличие от плоскости, где уравнение фигуры содержит две переменные х и у, в пространстве уравнение фигуры является уравнением с тремя переменными х, у и z.
Выведем уравнение плоскости, прямой и сферы в пространстве. Для получения уравнения плоскости рассмотрим в прямоугольной системе координат плоскость а (рис. 233) и определим свойство, с помощью которого можно описать принадлежность произвольной точки данной плоскости. Пусть ненулевой вектор 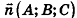 перпендикулярен а (то есть принадлежит прямой, перпендикулярной данной плоскости,— такой вектор называют вектором нормали или нормалью к плоскости а), а точка
перпендикулярен а (то есть принадлежит прямой, перпендикулярной данной плоскости,— такой вектор называют вектором нормали или нормалью к плоскости а), а точка 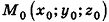 принадлежит данной плоскости.
принадлежит данной плоскости.
Так как 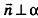 , то вектор га перпендикулярен любому вектору плоскости а. Поэтому если
, то вектор га перпендикулярен любому вектору плоскости а. Поэтому если 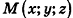 — произвольная точка плоскости а, то
— произвольная точка плоскости а, то 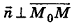 , то есть
, то есть 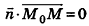 . Более того, если векторы
. Более того, если векторы 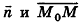 перпендикулярны, то, поскольку плоскость, проходящая через точку М0 перпендикулярно вектору
перпендикулярны, то, поскольку плоскость, проходящая через точку М0 перпендикулярно вектору 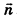 , единственна, имеем
, единственна, имеем 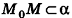 , то есть
, то есть 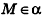 . Таким образом, уравнение
. Таким образом, уравнение 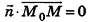 — критерий принадлежности точки М плоскости а. На основании этого векторного критерия выведем уравнение плоскости в пространстве.
— критерий принадлежности точки М плоскости а. На основании этого векторного критерия выведем уравнение плоскости в пространстве.
Теорема (уравнение плоскости в пространстве)
В прямоугольной системе координат уравнение плоскости имеет вид 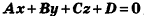 , где А, В, С и D — некоторые числа, причем числа А, В и С одновременно не равны нулю.
, где А, В, С и D — некоторые числа, причем числа А, В и С одновременно не равны нулю.
Доказательство:
Запишем в координатной форме векторное равенство 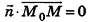 , где
, где 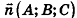 — вектор нормали к данной плоскости,
— вектор нормали к данной плоскости, 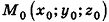 — фиксированная точка плоскости, M(x;y;z) — произвольная точка плоскости. Имеем
— фиксированная точка плоскости, M(x;y;z) — произвольная точка плоскости. Имеем 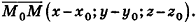
Следовательно, 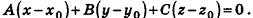
После раскрытия скобок и приведения подобных членов это уравнение примет вид: 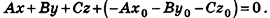
Обозначив числовое выражение в скобках через D, получим искомое уравнение, в котором числа А, В и С одновременно не равны нулю, так как 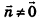 .
.
Покажем теперь, что любое уравнение вида Ах + Ву +Cz+D = 0 задает в пространстве плоскость. Действительно, пусть 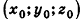 — одно из решений данного уравнения. Тогда
— одно из решений данного уравнения. Тогда 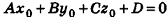 . Вычитая это равенство из данного, получим
. Вычитая это равенство из данного, получим 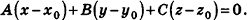 Так как это уравнение является координатной записью векторного равенства
Так как это уравнение является координатной записью векторного равенства 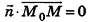 , то оно является уравнением плоскости, проходящей через точку
, то оно является уравнением плоскости, проходящей через точку 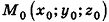 перпендикулярно вектору
перпендикулярно вектору 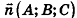 .
.
Обратим внимание на то, что в доказательстве теоремы приведен способ составления уравнения плоскости по данным координатам произвольной точки плоскости и вектора нормали.
Пример:
Напишите уравнение плоскости, которая перпендикулярна отрезку MN и проходит через его середину, если М{-1;2;3), N(5;-4;-1).
Решение:
Найдем координаты точки О — середины отрезка MN:
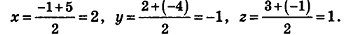
Значит, О (2; -1; l). Так как данная плоскость перпендикулярна отрезку MN, то вектор 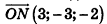 — вектор нормали к данной плоскости. Поэтому искомое уравнение имеет вид:
— вектор нормали к данной плоскости. Поэтому искомое уравнение имеет вид: 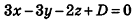 .
.
И наконец, так как данная плоскость проходит через точку О(2;-l;l), то, подставив координаты этой точки в уравнение, получим: 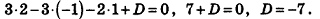
Таким образом, уравнение 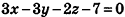 искомое.
искомое.
Ответ: 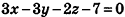
Заметим, что правильным ответом в данной задаче является также любое уравнение, полученное из приведенного умножением обеих частей на число, отличное от нуля.
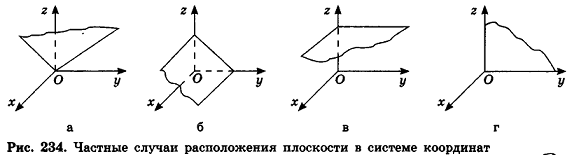
Значения коэффициентов А, В, С и D в уравнении плоскости определяют особенности расположения плоскости в системе координат. В частности:
- если
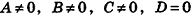 , уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а); - если один из коэффициентов А, В и С равен нулю, a
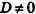 , плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали 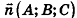 перпендикулярен оси Ох, а плоскость By + Cz + D = Q параллельна оси Ох (рис. 234, б)
перпендикулярен оси Ох, а плоскость By + Cz + D = Q параллельна оси Ох (рис. 234, б) - если два из коэффициентов А, В и С равны нулю, а
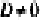 , плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали 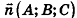 перпендикулярен плоскости Оху, а плоскость Cz+D = 0 параллельна плоскости Оху (рис. 234, в);
перпендикулярен плоскости Оху, а плоскость Cz+D = 0 параллельна плоскости Оху (рис. 234, в); - если два из коэффициентов А, В и С равны нулю и D = 0, плоскость совпадает с одной из координатных плоскостей: например, при условиях
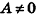 и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
Предлагаем вам самостоятельно составить полную таблицу частных случаев расположения плоскости Ax + By+Cz+D = 0 в прямоугольной системе координат в зависимости от значений коэффициентов А, В, С и D.
Пример: (о расстоянии от точки до плоскости)
Расстояние от точки 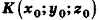 до плоскости а, заданной уравнением Ax + By + Cz+D = О, вычисляется по формуле
до плоскости а, заданной уравнением Ax + By + Cz+D = О, вычисляется по формуле
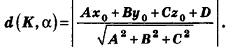 Докажите.
Докажите.
Решение:
Если 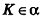 , то по уравнению плоскости
, то по уравнению плоскости 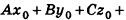
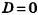 , откуда
, откуда 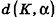 = 0.
= 0.
Если 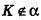 , то проведем перпендикуляр КМ к плоскости a,
, то проведем перпендикуляр КМ к плоскости a, 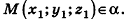 .
.
Тогда 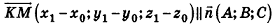 , поэтому
, поэтому 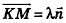 , то есть
, то есть 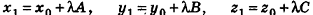 . Так как
. Так как 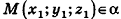 , то
, то 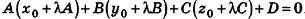 , откуда
, откуда 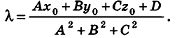
Таким образом, 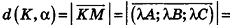
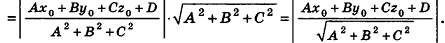
Рассмотрим теперь возможность описания прямой в пространстве с помощью уравнений.
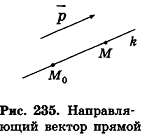
Пусть в пространстве дана прямая k (рис. 235). Выберем ненулевой вектор 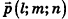 , параллельный данной прямой или принадлежащий ей (такой вектор называют направляющим вектором прямой k), и зафиксируем точку
, параллельный данной прямой или принадлежащий ей (такой вектор называют направляющим вектором прямой k), и зафиксируем точку 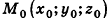 , принадлежащую данной прямой. Тогда произвольная точка пространства М (х; у; z) будет принадлежать прямой k в том и только в том случае, когда векторы
, принадлежащую данной прямой. Тогда произвольная точка пространства М (х; у; z) будет принадлежать прямой k в том и только в том случае, когда векторы 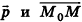 коллинеарны, то есть существует число t такое, что
коллинеарны, то есть существует число t такое, что 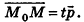
Представим это векторное равенство в координатной форме. Если ни одна из координат направляющего вектора не равна нулю, из данного равенства можно выразить t и приравнять полученные результаты:
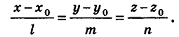
Эти равенства называют каноническими уравнениями прямой в пространстве.
Пример:
Напишите уравнение прямой, проходящей через точки А(1;-3;2) и В(-l;0;l).
Решение:
Так как точки А и В принадлежат данной прямой, то 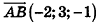 — направляющий вектор прямой АВ. Таким образом, подставив вместо
— направляющий вектор прямой АВ. Таким образом, подставив вместо 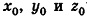 координаты точки А, получим уравнение прямой АВ:
координаты точки А, получим уравнение прямой АВ:
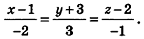
Ответ: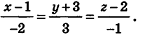
Заметим, что ответ в этой задаче может иметь и другой вид: так, в числителях дробей можно использовать координаты точки В, а как направляющий вектор рассматривать любой ненулевой вектор, коллинеарный 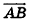 (например, вектор
(например, вектор 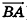 ).
).
Вообще, если прямая в пространстве задана двумя точками 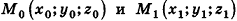 , то
, то 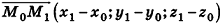 — направляющий вектор прямой, а в случае, если соответствующие координаты данных точек не совпадают, канонические уравнения прямой
— направляющий вектор прямой, а в случае, если соответствующие координаты данных точек не совпадают, канонические уравнения прямой 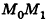 имеют вид
имеют вид 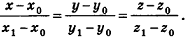
С помощью уравнений удобно исследовать взаимное расположение прямых и плоскостей в пространстве. Рассмотрим прямые 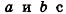 направляющими векторами
направляющими векторами 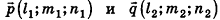 соответственно. Определение угла между данными прямыми связано с определением угла между их направляющими векторами. Действительно, пусть ф — угол между прямыми
соответственно. Определение угла между данными прямыми связано с определением угла между их направляющими векторами. Действительно, пусть ф — угол между прямыми 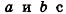 . Так как по определению
. Так как по определению 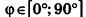 , а угол между векторами может быть больше 90°, то
, а угол между векторами может быть больше 90°, то 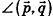 либо равен углу ср (рис. 236, а), либо дополняет его до 180° (рис. 236, б).
либо равен углу ср (рис. 236, а), либо дополняет его до 180° (рис. 236, б).
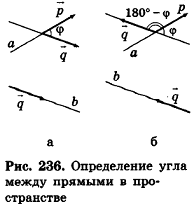
Так как cos(l80°-ф) = -coscp, имеем 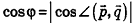 , то есть
, то есть
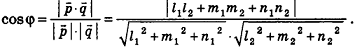
Отсюда, в частности, следует необходимое и достаточное условие перпендикулярности прямых 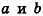 :
:
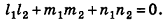
Кроме того, прямые 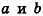 параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, то есть существует число t такое, что
параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, то есть существует число t такое, что 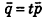 , или, при условии отсутствия у векторов р и q нулевых координат,
, или, при условии отсутствия у векторов р и q нулевых координат,
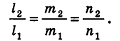
Проанализируем теперь отдельные случаи взаимного расположения двух плоскостей в пространстве. Очевидно, что если 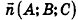 —вектор нормали к плоскости а, то все ненулевые векторы, коллинеарные л, также являются векторами нормали к плоскости а. Из этого следует, что две плоскости, заданные уравнениями
—вектор нормали к плоскости а, то все ненулевые векторы, коллинеарные л, также являются векторами нормали к плоскости а. Из этого следует, что две плоскости, заданные уравнениями 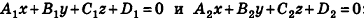 :
:
- совпадают, если существует число t такое, что
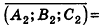
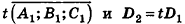 , или, если числа
, или, если числа 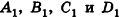 ненулевые
ненулевые 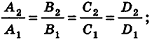
- параллельны, если существует число t такое, что
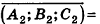
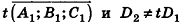 , или, если координаты
, или, если координаты 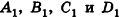 ненулевые,
ненулевые, 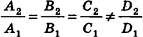 (на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где 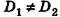 ).
).
В остальных случаях данные плоскости 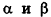 пересекаются, причем угол между ними связан с углом между векторами нормалей
пересекаются, причем угол между ними связан с углом между векторами нормалей 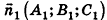 и
и 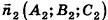 . Предлагаем вам самостоятельно обосновать формулу для определения угла между плоскостями
. Предлагаем вам самостоятельно обосновать формулу для определения угла между плоскостями 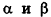 :
:
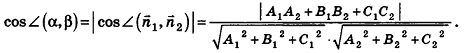
В частности, необходимое и достаточное условие перпендикулярности плоскостей 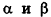 выражается равенством
выражается равенством 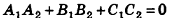 .
.
Заметим также, что прямая в пространстве может быть описана как линия пересечения двух плоскостей, то есть системой уравнений
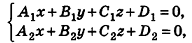
где векторы 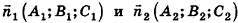 не коллинеарны.
не коллинеарны.
Пример:
Напишите уравнение плоскости, которая проходит через точку М(4;2;3) и параллельна плоскости x-y + 2z-S = 0.
Решение:
Так как искомая плоскость параллельна данной, то вектор нормали к данной плоскости 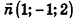 является также вектором нормали к искомой плоскости. Значит, искомое уравнение имеет вид
является также вектором нормали к искомой плоскости. Значит, искомое уравнение имеет вид 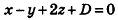 . Так как точка М принадлежит искомой плоскости, ее координаты удовлетворяют уравнению плоскости, то есть 4-2 + 2-3 + 2) = 0, D = -8. Следовательно, уравнение x-y+2z-8=0 искомое.
. Так как точка М принадлежит искомой плоскости, ее координаты удовлетворяют уравнению плоскости, то есть 4-2 + 2-3 + 2) = 0, D = -8. Следовательно, уравнение x-y+2z-8=0 искомое.
Ответ: x-y+2z-8 = 0.
Аналогично уравнению окружности на плоскости, в пространственной декартовой системе координат можно вывести уравнение сферы с заданным центром и радиусом.
Теорема (уравнение сферы)
В прямоугольной системе координат уравнение сферы радиуса R с центром в точке 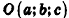 имеет вид
имеет вид 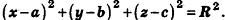 Доказательство
Доказательство
Пусть 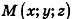 — произвольная точка сферы радиуса R с центром
— произвольная точка сферы радиуса R с центром 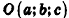 (рис. 237). Расстояние между точками О и М вычисляется по формуле
(рис. 237). Расстояние между точками О и М вычисляется по формуле 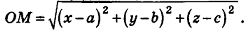
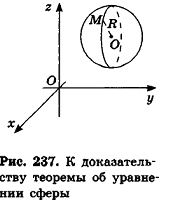
Так как OM=R, то есть ОМ2 = R2, то координаты точки М удовлетворяют уравнению 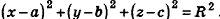 . Если же точка М не является точкой сферы, то
. Если же точка М не является точкой сферы, то 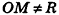 , значит, координаты точки М не удовлетворяют данному уравнению.
, значит, координаты точки М не удовлетворяют данному уравнению.
Следствие
Сфера радиуса R с центром в начале координат задается уравнением вида
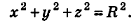
Заметим, что фигуры в пространстве, как и на плоскости, могут задаваться не только уравнениями, но и неравенствами. Например, шар радиуса R с центром в точке 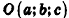 задается неравенством
задается неравенством 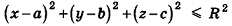 (убедитесь в этом самостоятельно).
(убедитесь в этом самостоятельно).
Пример:
Напишите уравнение сферы с центром А (2;-8; 16), которая проходит через начало координат.
Решение:
Так как данная сфера проходит через точку 0(0;0;0), то отрезок АО является ее радиусом. Значит,
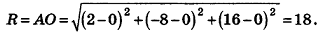
Таким образом, искомое уравнение имеет вид:
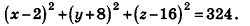
Ответ: 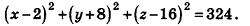
Доказательство формулы объема прямоугольного параллелепипеда
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
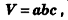
где 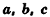 — измерения параллелепипеда.
— измерения параллелепипеда.
Доказательство:
Докажем сначала, что объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
Пусть 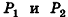 — два прямоугольных параллелепипеда с равными основаниями и объемами
— два прямоугольных параллелепипеда с равными основаниями и объемами 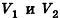 соответственно. Совместим данные параллелепипеды. Для этого достаточно совместить их основания. Теперь рассмотрим объемы параллелепипедов
соответственно. Совместим данные параллелепипеды. Для этого достаточно совместить их основания. Теперь рассмотрим объемы параллелепипедов 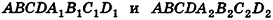 (рис. 238). Для определенности будем считать, что
(рис. 238). Для определенности будем считать, что 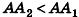 . Разобьем ребро
. Разобьем ребро 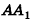 на n равных отрезков. Пусть на отрезке
на n равных отрезков. Пусть на отрезке 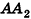 лежит m точек деления. Тогда:
лежит m точек деления. Тогда:
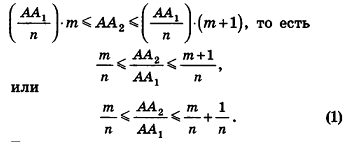
проведем через точки деления параллельные основанию ABCD (рис. 239). Они разобьют параллелепипед 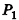 на n равных параллелепипедов. Каждый из них имеет объем
на n равных параллелепипедов. Каждый из них имеет объем 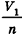 . Очевидно, что параллелепиппед
. Очевидно, что параллелепиппед 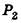 содержит в себе объединение m параллелепипедов и сам содержится в объединении
содержит в себе объединение m параллелепипедов и сам содержится в объединении 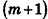 параллелепипедов.
параллелепипедов.
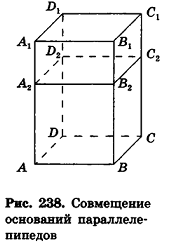
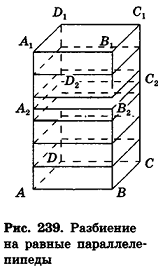
Таким образом, 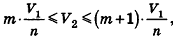 откуда
откуда 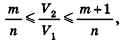 или
или 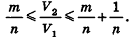
Сравнивая выражения (1) и (2), видим, что оба отношения 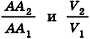 находятся между
находятся между 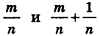 , то есть отличаются не больше чем на
, то есть отличаются не больше чем на 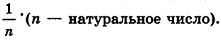 Докажем методом от противного, что эти отношения равны.
Докажем методом от противного, что эти отношения равны.
Допустим, что это не так, то есть 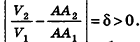 Тогда найдется такое натуральное число n, что
Тогда найдется такое натуральное число n, что 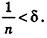 Отсюда
Отсюда 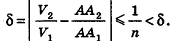 Из полученного противоречия следует, что
Из полученного противоречия следует, что 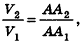 то есть объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
то есть объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
Рассмотрим теперь прямоугольные параллелепипеды с измерениями 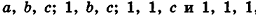 объемы которых равны V,
объемы которых равны V, 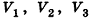 соответственно (рис. 240).
соответственно (рис. 240).
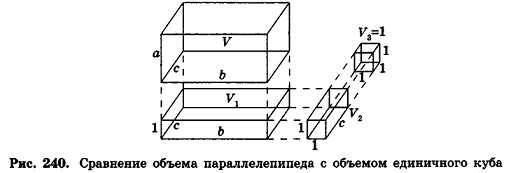
По аксиоме объема V3 =1. По доказанному 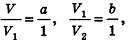
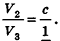 Перемножив эти отношения, получим: V = abc.
Перемножив эти отношения, получим: V = abc.
Теорема доказана.
* Выберем 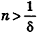 , например,
, например, 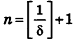 , где
, где 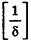 — целая часть дроби
— целая часть дроби 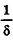 .
.
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
- Площадь многоугольника
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии
