
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
1 мая
Бесплатные курсы подготовки к ЕГЭ и ОГЭ
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Площадь поверхности составного многогранника
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 2 № 25541 

i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25541: 25543 25549 25545 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
2
Тип 2 № 25561 

i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25561: 25563 25569 512372 … Все
Источник: ЕГЭ по математике 10.06.2013. Вторая волна. Центр. Вариант 601
Решение
·
Видеокурс
·
Помощь
3
Тип 2 № 25581 

i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25581: 25583 25589 25585 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
4
Тип 2 № 25601 

i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25601: 25603 25609 505146 … Все
Решение
·
7 комментариев
·
Видеокурс
·
Помощь
5
Тип 2 № 25621 

i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25621: 25623 25625 25629 … Все
Решение
·
3 комментария
·
Видеокурс
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
ЕГЭ Профиль №5. Площадь поверхности и объем составного многогранника
Скачать файл в формате pdf.
ЕГЭ Профиль №5. Площадь поверхности и объем составного многогранника
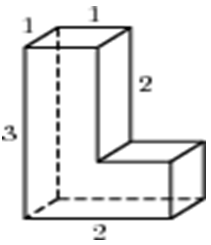
| Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 18. |
 |
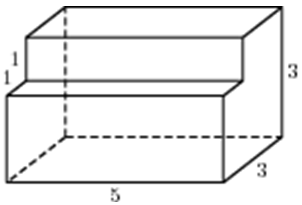
| Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 76. |
 |
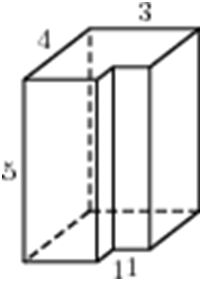
| Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 92. |
 |
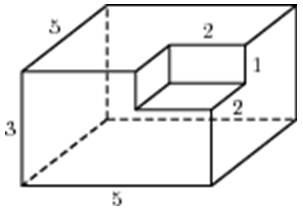
| Задача 4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 110. |
 |
| Задача 5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 94. |
 |
| Задача 6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 132. |
 |
| Задача 7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 114. |
 |
| Задача 8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 48. |
 |
| Задача 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 84. |
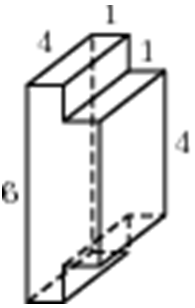 |
| Задача 10. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 96. |
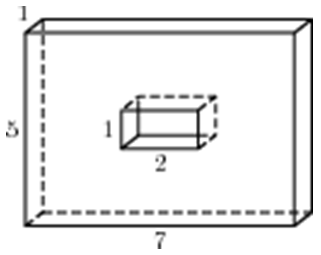 |
| Задача 11. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 124. |
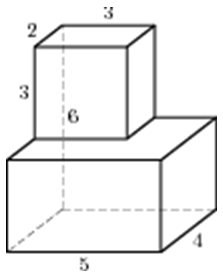 |
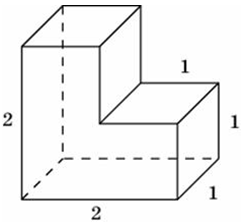
| Задача 12. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ
ОТВЕТ: 14. |
 |
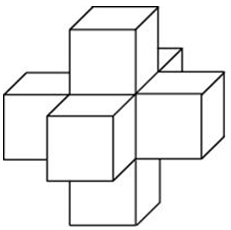
| Задача 13. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Ответ
ОТВЕТ: 30. |
 |
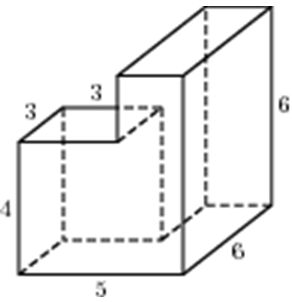
| Задача 14. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 162. |
 |
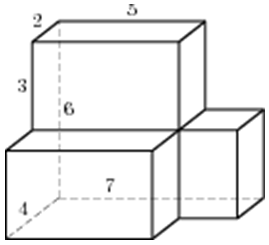
| Задача 15. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 156. |
 |
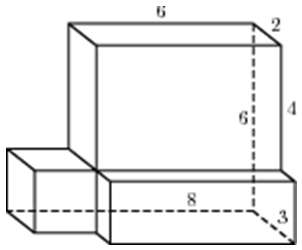
| Задача 16. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 152. |
 |
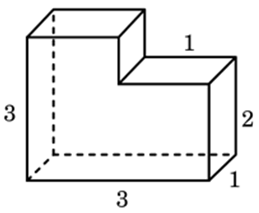
| Задача 17. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ
ОТВЕТ: 8. |
 |
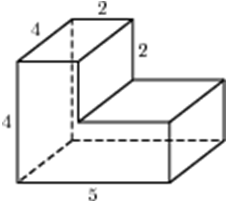
| Задача 18. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 56. |
 |
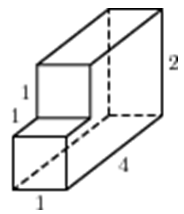
| Задача 19. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 7. |
 |
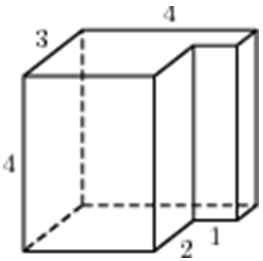
| Задача 20. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 40. |
 |
| Задача 21. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 34. |
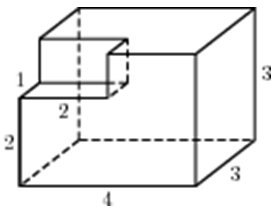 |
| Задача 22. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 36. |
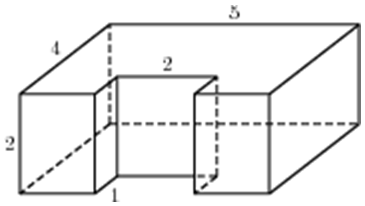 |
| Задача 23. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 90. |
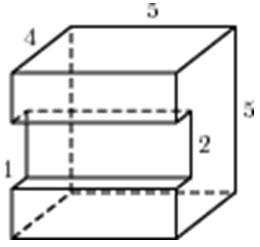 |
| Задача 24. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 18. |
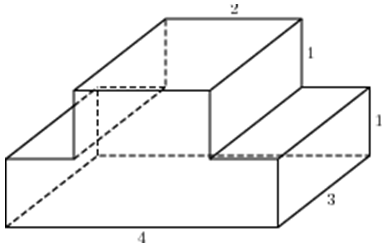 |
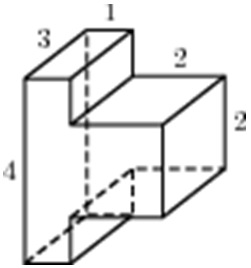
| Задача 25. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 24. |
 |
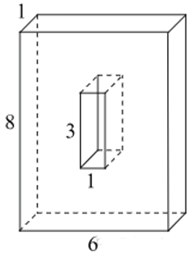
| Задача 26. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 45. |
 |
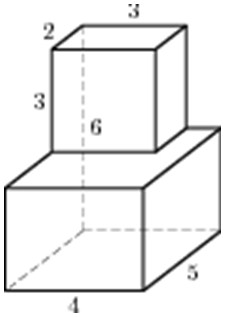
| Задача 27. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 78. |
 |
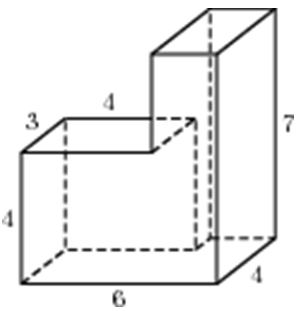
| Задача 28. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 104. |
 |
| Задача 29. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 87. |
 |
| Задача 30. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 114. |
 |
| Задача 31. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 78. |
 |
Приветствую, сообщество Хакнем!
Сегодня в рубрике #хакнем_математика продолжим цикл статей, посвященных решению задач из ОГЭ и ЕГЭ по математике. Иногда в комментариях читатели спрашивают — зачем вы это пишите, и кому это нужно? Отвечаю — поверьте, кому-то это точно нужно! И даже, если моя статья поможет хоть 5-ти учащимся, я буду рада.
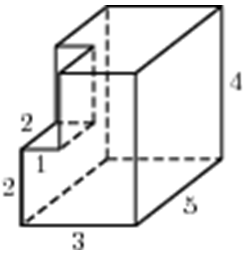
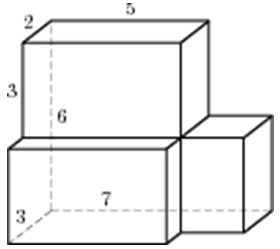
Недавно мой сын 11-классник пришёл ко мне с вопросом по задаче 8 (стереометрия) из ЕГЭ профильного уровня: «Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится». Вот эта задача:
Задача 1
При решении этой задачи нам необходимо знать одну лишь формулу — формулу нахождения площади полной поверхности прямоугольного параллелепипеда с измерениями a, b, c: S = 2 ×(ab+ bc+ ac).
Как рассуждал сын? Он нашёл площадь нижнего параллелепипеда и площадь верхнего, и сложил результаты:
1. Площадь нижнего с измерениями 5×4×3 равна: S = 2 (5×4 + 4×3 + 5×3) = 94
2. Площадь верхнего с измерениями 3×2×3 равна: S = 2 (3×2 + 2×3 + 3×3) = 42
Если сложить эти два результата, получится 136. Где же ошибка?
Ошибка в том, что в найденных площадях и нижнего и верхнего параллелепипедов содержится площадь прямоугольника со сторонами 2×3 (S = 6, показана на рисунке красным, которая в площадь поверхности многогранника не входит.
Таким образом, из полученного результата надо вычесть две таких площади: 136 – 2×6 = 124. Ответ: 124.
Разберём ещё подобные задачи.
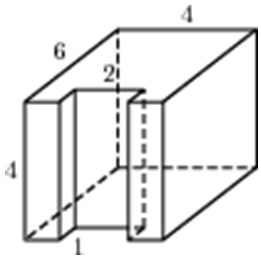
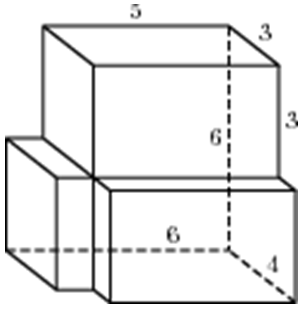
Задача 2
Решение:
Чтобы упростить решение задачи, достроим наш многогранник до параллелепипеда с измерениями 2×1×3.
Его площадь равна: S = 2 × (2×1 + 1×3 + 2×3) = 22.
Осталось вычесть площади «лишних» прямоугольников. Посмотрите на рисунок:
- прямоугольник (его площадь), показанный розовой штриховкой, оставляем, так он входит в многогранник;
- голубой тоже нужен;
- а вот 2 зелёных (со сторонами 1 × 2) — лишние, их площади нужно вычесть.
Итак, S = 22 – 2 × (1×2) = 22 – 4 = 18.
Ответ: 18.
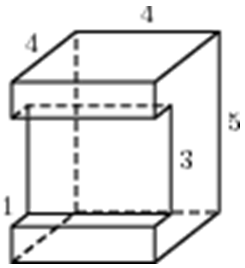
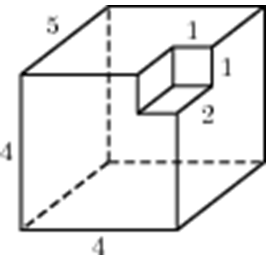
Задача 3
Решение:
А эту задачу решим немного другим способом. Если вы внимательно посмотрите на рис. в условии, то увидите, что это параллелепипед с вырезанным уголком (ну или с вдавленным). И если бы была такая возможность, и мы могли бы взять за уголок и потянуть, как показано стрелкой на рисунке, то параллелепипед станет «целым».
А это значит, чтобы найти искомую площадь поверхности многогранника нужно найти площадь поверхности прямоугольного параллелепипеда с измерениями 5×5×3:
S = 2 × (5×5 + 5×3 + 5×3) = 110.
Ответ: 110.
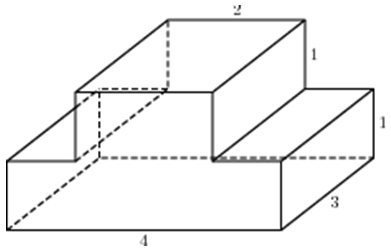
Задача 4
Решение:
Достроим снова для наглядности многогранник до прямоугольного параллелепипеда с измерениями 4×6×4. Его площадь:
S = 2×(4×6 + 6×4 + 4×4) = 128.
- площадь жёлтого прямоугольника уже вошла в найденную площадь поверхности параллелепипеда;
- 2 площади зелёных прямоугольников со сторонами 1×4 (S = 4) нужно добавить к найденной площади параллелепипеда;
- 2 площади сиреневых прямоугольников со сторонами 1×2 (S = 2) — лишние, и поскольку они вошли в площадь параллелепипеда, а в искомом многограннике их на самом деле нет, то их вычтем.
Итак, S = 128 + 2×4 – 2×2 = 132.
Ответ: 132.
А в заключении приведу задачу с условием и рисунком, что и в задаче 1, но найти нужно объём многогранника.
Задача 5.
Решение:
Здесь всё намного проще. Достаточно найти объёмы 2-х параллелепипедов с измерениями 4×5×3 и 3×2×3 и сложить их.
Вспоминаем, что объём прямоугольного параллелепипеда с измерениями a, b, c находится по формуле: V = a×b×c.
V1 = 4 × 5 × 3 = 60;
V2 = 3 × 2 × 3 = 18;
V = 60 + 18 = 78.
Ответ: 78.
Не путайте на экзамене объём и площадь поверхности.
Вы всегда можете распечатать решение этих задач из Дзен или скопировать себе ссылку на статью, а при подготовке к экзамену ещё раз перечитать решение и вспомнить.
Удачи!
Кстати, принесла эти задачи своим коллегам на работу (не в школу, так как моя работа никак с ней не связана), так вот они с интересом эти задачки порешали. В ход пошли различные подручные “модели” и сложенные фигурки из бумаги. Ведь самое сложное в них — понять что лишнее, а что уже входит. Хорошая гимнастика ума!
Если нашли ошибку или опечатку, пишите в комментариях, буду благодарна.
#хакнем_математика (👈 подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике 🥳
Автор: #ирина_чудневцева координатор канала Хакнем Школа, 42 года, город Ярославль
Похожие статьи автора:
Если у вас есть познавательный материал, тёплые воспоминания и интересные истории из школьной жизни, которые вы хотели бы опубликовать в нашем канале, или вы просто хотите стать автором канала, напишите нам об этом 👉 story@haknem.com
Такое задание можно выполнить несколькими способами:
а) Вычислить отдельные составляющие многогранника без достроения
б) Достроить до полноценной фигуры (параллелепипеда) и вычесть площадь поверхности фигуры, которую мы “приклеили” в изначально заданному многограннику
Воспользуемся первым способом:
Разметим поверхности для удобства как показано на рисунке и по отдельности вычислим площади составляющих общую поверхность поверхностей составляющих, после чего сложим полученные площади и получим ответ.

S1 = 1*2 = 2
Таких поверхностей у нас две => S1*2 = 2*2 = 4
S2 = 1*1 = 1
Аналогично, две поверхности => S2*2 = 1*2 = 2
S3 = 2*1 = 2
S4 = 1*2 = 2
Две поверхности => S4*2 = 2*2 = 4
S5 = 1*1 = 1
Аналогично, S5*2 = 1*2 = 2
S6 = 2*1 = 2, S6*2 = 2*2 = 4
Теперь сложим все площади: 4 + 2 + 2 + 4 + 2 + 4 = 18
07
Сен 2013
Категория: 02 Стереометрия
02. Составные многогранники. Площадь поверхности. Объем
2013-09-07
2022-09-11
Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
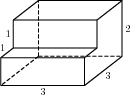
Решение: + показать
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение: + показать
Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение: + показать
Задача 4. Из единичного куба вырезана правильная четырехугольная призма со стороной основания и боковым ребром
Найдите площадь поверхности оставшейся части куба.
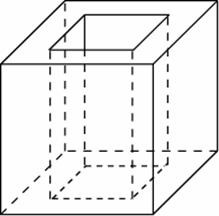
Решение: + показать
Задача 5. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раз?
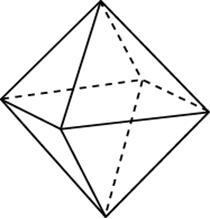
Решение: + показать
Задача 6. Площадь поверхности тетраэдра равна Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра Видео*
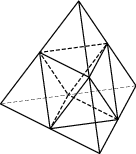
Решение: + показать
Задача 7. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
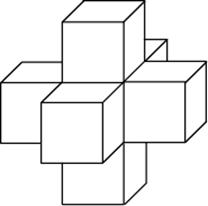
Решение: + показать
Задача 8. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение: + показать
Задача 9. Объем тетраэдра равен Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.

Решение: + показать
Задача 10. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы
, площадь основания которой равна 3, а боковое ребро равно 7.

Решение: + показать
 Вы можете пройти тест “Cоставные многогранники”
Вы можете пройти тест “Cоставные многогранники”
Автор: egeMax |
комментариев 14
