Как найти площадь многоугольника егэ - Сайт, где вы сможете решить свои вопросы

Каталог заданий.
Многоугольники: вычисление площадей

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Источники:

Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень;

Пройти тестирование по этим заданиям

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 – 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

6. Геометрия на плоскости (планиметрия). Часть II

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Использование различных формул площадей многоугольников

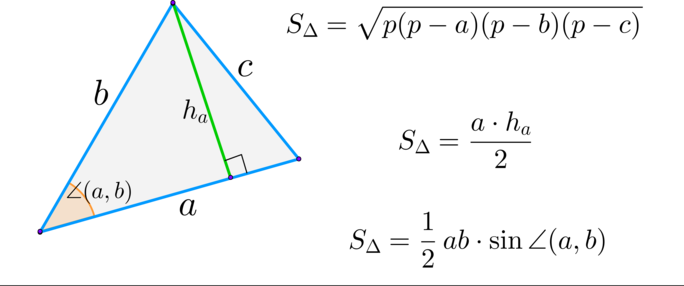
(blacktriangleright) Треугольник:

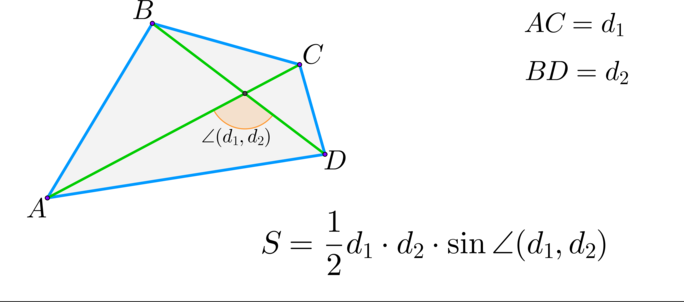
(blacktriangleright) Произвольный выпуклый четырехугольник:

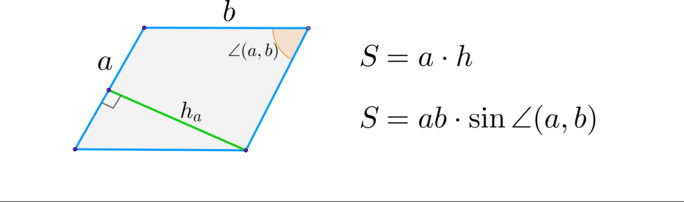
(blacktriangleright) Параллелограмм:

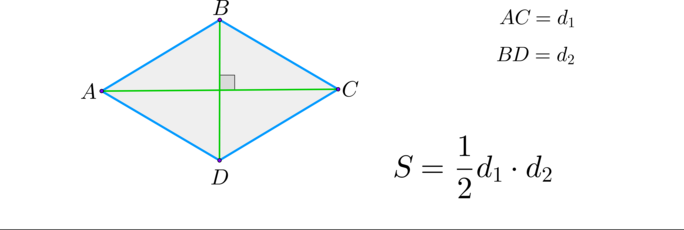
(blacktriangleright) Ромб:

(blacktriangleright) Прямоугольник:

(blacktriangleright) Квадрат:

(blacktriangleright) Трапеция:

Задание
1

#2269

Уровень задания: Легче ЕГЭ

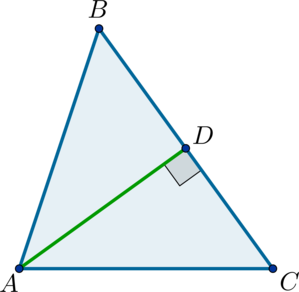
В треугольнике (ABC): (AD) – высота, (cos{angle DAC} = 0,7), (AC
= 6), (BC = 9). Найдите площадь треугольника (ABC).

Так как (AD) перпендикулярна (DC), то (sin{angle C} = cos{angle
DAC} = 0,7).

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними,
тогда площадь треугольника (ABC) равна (0,5cdot 6 cdot 9 cdot 0,7
= 18,9).

Ответ: 18,9

Задание
2

#2270

Уровень задания: Легче ЕГЭ

Периметр треугольника (ABC) равен (250), одна из его сторон равна (120), ещё одна сторона равна (17). Найдите его площадь.

Третья сторона треугольника равна (250 – 120 – 17 = 113).
По формуле Герона (S_{triangle ABC} = sqrt{p(p – AB)(p – BC)(p –
AC)}), где (p) – полупериметр треугольника (ABC).

Для данного треугольника

(S_{triangle ABC} = sqrt{125cdot (125 – 120)cdot (125 – 17)cdot (125 – 113)} = sqrt{125cdot 5 cdot 12 cdot 108} =)

(= 25sqrt{12cdot 108} = 100sqrt{3cdot 27} = 900.)

Ответ: 900

Задание
3

#2279

Уровень задания: Равен ЕГЭ

Найдите высоту треугольника, проведенную к стороне длиной (8), если высота, проведенная к стороне длиной (6), равна (4).

Т.к. площадь треугольника равна полупроизведению высоты и стороны, к которой эта высота проведена, то с одной стороны площадь равна [S=dfrac12cdot 6cdot 4,]

а с другой [S=dfrac12cdot 8cdot h,]

где (h) – высота, которую нужно найти. Таким образом, получаем следующее равенство:

[dfrac12cdot 6cdot 4=dfrac12cdot 8cdot h quad Leftrightarrow quad h=3.]

Ответ: 3

Задание
4

#2268

Уровень задания: Равен ЕГЭ

В треугольнике (ABC): (AC = 4), (AB = 6), (cos{angle BAC} =
dfrac{sqrt{15}}{4}). Найдите площадь треугольника (ABC).

Из основного тригонометрического тождества:
(sin^2angle BAC = 1 – dfrac{15}{16}), тогда (sinangle BAC = pm
0,25). Так как (angle BAC in (0^{circ}; 180^{circ})), то (sinangle BAC = 0,25).

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними,
тогда площадь треугольника (ABC) равна (0,5cdot 4 cdot 6 cdot
0,25 = 3).

Ответ: 3

Задание
5

#2280

Уровень задания: Равен ЕГЭ

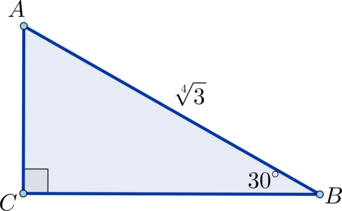
В прямоугольном треугольнике гипотенуза равна (sqrt[4]3), а один из углов равен (30^circ). Найдите площадь этого треугольника.

Т.к. катет, лежащий против угла в (30^circ), равен половине гипотенузы, то (AC=0,5cdot AB=0,5cdot sqrt[4]3).

Т.к. (angle A=90^circ -angle B=60^circ), то площадь равна [S=dfrac12cdot ACcdot ABcdot sin 60^circ=dfrac12cdot
0,5cdot sqrt[4]3cdot sqrt[4]3cdot
dfrac{sqrt3}2=dfrac38=0,375.]

Ответ: 0,375

Задание
6

#2274

Уровень задания: Равен ЕГЭ

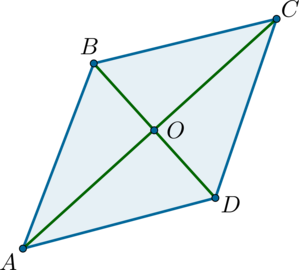
В ромбе (ABCD): (O) – точка пересечения диагоналей, (BD = 8), (mathrm{tg}, angle BDC = 3). Найдите площадь ромба (ABCD).

В ромбе диагонали пересекаются под прямым углом и точкой пересечения делятся пополам, тогда (OD = 4), (dfrac{CO}{OD} = mathrm{tg},
angle BDC = 3), откуда (CO = 12), следовательно, (AC = 24).

Площадь ромба равна половине произведения его диагоналей, тогда [S_{ABCD} = 0,5cdot 8cdot 24 = 96.]

Ответ: 96

Задание
7

#3326

Уровень задания: Равен ЕГЭ

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен (150^circ). Найдите боковую сторону этого треугольника, если его площадь равна (100).

Пусть (a) – боковая сторона треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, [dfrac12cdot a^2cdot sin30^circ=S=100quadRightarrowquad
a^2=400quadRightarrowquad a=20]

Ответ: 20

Подготовка выпускников к сдаче аттестационного испытания по математике, как правило, начинается с повторения базовых определений и формул, в том числе и тех, которые позволяют произвести вычисление площадей плоских фигур в ЕГЭ. Данный раздел геометрии изучается в средней школе. Неудивительно, что с необходимостью повторения основных формул для правильного нахождения площади любого многоугольника сталкиваются многие выпускники. Умея выполнять расчеты с их применением, учащиеся смогут рассчитывать на получение конкурентных баллов по итогам сдачи аттестационного испытания.

Готовьтесь вместе с образовательным порталом «Школково»

Занимаясь перед сдачей экзамена, многие учащиеся сталкиваются с проблемой поиска определений и формул, которые позволяют выполнить вычисление площади правильного многоугольника в ЕГЭ. Школьный учебник далеко не всегда оказывается под рукой в нужный момент.

Вместе с образовательным порталом «Школково» подготовка к экзамену будет легкой и эффективной. Здесь представлен весь необходимый материал, подобранный и изложенный нашими специалистами в максимально понятной форме. Какая именно формула для нахождения площади многоугольника потребуется при работе с треугольником, четырехугольником, параллелограммом, ромбом, прямоугольником, квадратом, трапецией? Всю эту информацию вы найдете в разделе «Теоретическая справка». Ознакомившись с ней, выпускники смогут восполнить пробелы в знаниях.

Чтобы научиться быстро находить правильный ответ, необходимо также попрактиковаться в решении задач на нахождение площади фигур. Большая подборка упражнений представлена в разделе «Каталог». Для каждой задачи на нахождение площади фигур, например, вычисление площади параллелограмма, наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень упражнений на сайте постоянно дополняется и обновляется.

Любое задание, например, на подобие площадей подобных треугольников, выпускники могут сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти интересующее упражнение, например, с целью обсуждения хода его решения с преподавателем.

УСТАЛ? Просто отдохни

Источник

Площади многоугольников на координатной сетке

5 февраля 2011

Многоугольники на координатной сетке — это самые простые задачи B5. Существует сразу несколько методов решения таких задачи, в том числе универсальный, описанный ниже. Для начала определимся с терминологией:

Многоугольник — фигура на плоскости, ограниченная замкнутой ломаной.

Большинство многоугольников, встречающихся в ЕГЭ, являются выпуклыми, т.е. не имеют внутренних углов размером больше 180°, а все вершины многоугольника лежат в узлах координатной сетки. Кроме того, ломаная, ограничивающая многоугольник, не имеет самопересечений. Все это значительно упрощает задачу.

Для решения всех задач этого типа достаточно выполнить четыре простых шага:

Описать вокруг многоугольника прямоугольник, стороны которого параллельны осям координат (линиям сетки). При этом желательно, чтобы на каждой стороне прямоугольника присутствовала хотя бы одна вершина исходной фигуры;
Разбить внутреннее пространство прямоугольника, не занятое исходной фигурой, на квадраты и треугольники. Лучше, если все линии разбиения будут параллельны осям координат;
Найти площадь каждого элемента разбиения. Сложив эти площади, получим площадь всего разбиения;
Наконец, из площади прямоугольника вычесть площадь разбиения — это и будет площадью исходной фигуры.

Несмотря на большое количество элементов разбиения, вычисление его площади — достаточно тривиальная задача.

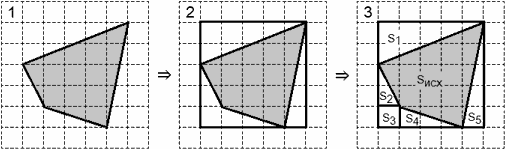
Проиллюстрируем каждый шаг решения:

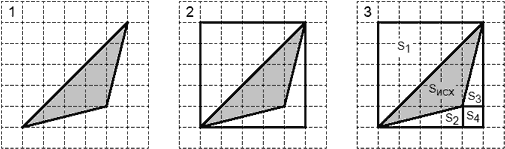
Последним шагом найдем площадь исходной фигуры: S_исх = S − (S₁ + S₂ + S₃ + S₄ + S₅), где S — площадь описанного прямоугольника. Осталось вычислить площадь большого прямоугольника и элементов разбиения. Эти несложные расчеты предлагается выполнить читателю в качестве упражнения.

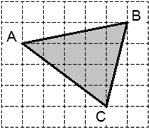
Задача. Найти площадь треугольника ABC, изображенного на рисунке:

Обозначение треугольника можно опустить, поскольку оно нам не потребуется. Приведем первые три шага:

Итак, S_исх = S − (S₁ + S₂ + S₃), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения:

S₁ = ½ · 1 · 5 = 2,5; S₂ = ½ · 3 · 4 = 6; S₃ = ½ · 1 · 4 = 2; S = 5 · 4 = 20.

Наконец, найдем площадь треугольника: S_исх = 20 − (2,5 + 6 + 2) = 9,5.

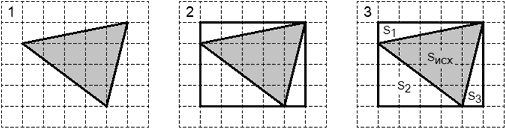
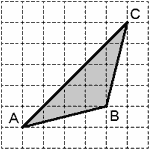
Задача. Найти площадь треугольника ABC, изображенного на рисунке:

Снова выполняем первые три шага. Заметим, что угол ABC — тупой, поэтому в разбиении присутствует квадрат. Имеем:

Очевидно, S_исх = S − (S₁ + S₂ + S₃ + S₄), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения:

S₁ = ½ · 5 · 5 = 12,5; S₂ = ½ · 4 · 1 = 2; S₃ = ½ · 1 · 4 = 2; S₄ = 1 · 1 = 1; S = 5 · 5 = 25.

Площадь треугольника: S_исх = 25 − (12,5 + 2 + 2 + 1) = 7,5.

Смотрите также:

Задача B5: вычисление площади методом обводки
Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
Системы линейных уравнений: основные понятия
Тест к уроку «Знаки тригонометрических функций» (1 вариант)
Координаты вершин правильного тетраэдра
Задача B2 про комиссию в терминале

Источник

Инфоурок

›

Геометрия

›Презентации›Подготовка к ЕГЭ “Разные способы нахождения площади многоугольников”

Подготовка к ЕГЭ “Разные способы нахождения площади многоугольников”

Скачать материал

Сейчас обучается 140 человек из 43 регионов

Сейчас обучается 50 человек из 26 регионов

Описание презентации по отдельным слайдам:

1 слайд

Разные способы нахождения
площади многоугольников

подготовка к ЕГЭ по математике
Учитель математики
МКОУ «Новопоселковая сош»
Чубанова А.М.
2 слайд

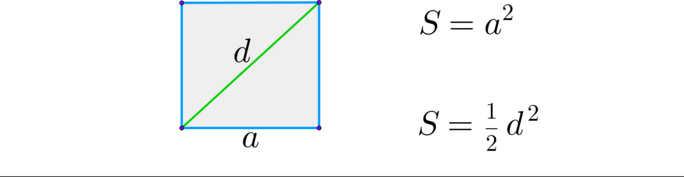
Площадь прямоугольника: 𝑆=𝑎∙𝑏, где
a и b – стороны прямоугольника.
Площадь квадрата: 𝑆= 𝑎 2

Задачи. На клетчатой бумаге с клетками размером 1 см × 1 см изображена фигура. Найдите ее площадь в квадратных сантиметрах.

1)2)

𝑎= 1+4 = 5 см,
𝑏= 16+4 =2 5 см, 𝑎= 1+9 = 10 см,
S= 5 ∙2 5 =10 см 2 S = 10 2 =10 см 2
Нахождение площади по формулам
3 слайд

Площадь треугольника: 𝑆= 1 2 𝑎∙ℎ, где
a – основание, h – высота треугольника.

Задачи. На клетчатой бумаге с клетками размером 1 см × 1 см изображена фигура. Найдите ее площадь в квадратных сантиметрах.

1) 2) 3)

S = 1 2 ∙4∙9=18 см 2 S = 1 2 ∙3∙3=4,5 см 2 S = 1 2 ∙2 2 ∙6 2 =12 см 2

Нахождение площади по формулам
4 слайд

Площадь параллелограмма: 𝑆=𝑎∙ℎ, где
a – сторона, h – высота параллелограмма, проведенная к этой стороне.

Задачи. Найдите площадь четырехугольника, изображенного на рисунке

Нахождение площади по формулам
𝑆= 2∙3=6 см 2 𝑆= 3∙5=15 см 2
5 слайд

Площадь трапеции: 𝑆= 1 2 𝑎+𝑏 ∙ℎ, где
a, b – основания, h – высота трапеции.

Задачи. На клетчатой бумаге с клетками размером 1 см × 1 см изображена фигура. Найдите ее площадь в квадратных сантиметрах.

S = 1 2 1+4 ∙6=15 см 2 S = 1 2 2+5 ∙4=14 см 2
Нахождение площади по формулам
6 слайд

Площадь четырехугольника, диагонали которого взаимно перпендикулярны: 𝑆= 1 2 𝑑 1 ∙ 𝑑 2 .

Задачи. На клетчатой бумаге с клетками размером 1 см × 1 см изображена фигура. Найдите ее площадь в квадратных сантиметрах.

S = 1 2 ∙4∙6=12 см 2 S = 1 2 ∙ 2 ∙3 2 =3 см 2

Нахождение площади по формулам
7 слайд

Если разбить фигуру на несколько фигур, то площадь всей фигуры равна сумме площадей ее частей.
Задачи. На клетчатой бумаге с клетками размером 1 см × 1 см изображена фигура. Найдите ее площадь в квадратных сантиметрах.

𝑆 1 = 1 2 ∙2∙5=5 см 2 ; 𝑆 2 = 1 2 ∙3∙5=7,5 см 2 𝑆 1 = 1 2 ∙2∙3=3 см 2
𝑆 1 + 𝑆 2 =12,5 см 2 2∙𝑆 1 =6 см 2

Сложение площадей
8 слайд

Площадь многоугольника можно найти, вписав его в прямоугольник, и вычитая площади соответствующих лишних частей.
Задачи. На клетчатой бумаге с клетками размером 1 см × 1 см изображена фигура. Найдите ее площадь в квадратных сантиметрах.
𝑆 прям =7∙6=42 см 2
𝑆 1 = 1 2 ∙6∙4=12 см 2
𝑆 2 = 1 2 ∙7∙4=14 см 2
𝑆 3 =2∙3=6 см 2
S=42−12−14−6=10 см 2

Вычитание площадей
𝑆 2
𝑆 1
𝑆 3
S
9 слайд

Георг Пик – австрийский математик (1859-1942)
Теорема Пика (1899) о методе нахождения пощади многоугольника, нарисованного «по клеточкам» так, что вершины находятся в узлах.
Формула Пика: S = v + 𝟎,𝟓𝒈 – 1, где
v – это количество узлов внутри фигуры,
g – количество узлов на границе фигуры
(считая и вершины многоугольника)
В данном примере v =7, 𝒈 = 8, S = 10.

Задача. Найти площадь фигуры методом Пика:
v =10, 𝒈 = 10,
S = 10 + 0,5•10 -1= 14 см 2

Метод Пика
10 слайд

Задачи. На клетчатой бумаге с клетками размером 1 см × 1 см изображена фигура. Найдите ее площадь в квадратных сантиметрах.

v =7, 𝒈 = 8, v =12, 𝒈 = 4,
S = 7 + 0,5•8 -1= 10 см 2 S = 12 + 0,5•4 -1= 12 см 2

v =17, 𝒈 = 4,
S = 17 + 0,5•4 -1= 18 см 2

Метод Пика
11 слайд

Спасибо за внимание!

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 262 555 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

06.05.2019
326
3

Рейтинг:
5 из 5

05.05.2019
117
2

05.05.2019
329
4

05.05.2019
600
1

05.05.2019
1036
8

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Этика делового общения»
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС медицинских направлений подготовки»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»

Настоящий материал опубликован пользователем Чубанова Альмина Магомедтагировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 4 года и 1 месяц
- Подписчики: 0
- Всего просмотров: 3402
- Всего материалов:
  
  9

Источник

Использование различных формул площадей многоугольников

Готовьтесь вместе с образовательным порталом «Школково»

Площади многоугольников на координатной сетке

Подготовка к ЕГЭ “Разные способы нахождения площади многоугольников”

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Вам будут интересны эти курсы:

Вам также может понравиться

Как составить блок схему для чайников

Как правильно составить смету на ремонт дома

Как найти свой номер паспорта по фио

Добавить комментарий Отменить ответ