Как найти площадь многоугольника формула через радиус - Сайт, где вы сможете решить свои вопросы

На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Содержание:

калькулятор площади правильного многоугольника
формула площади правильного многоугольника через длину стороны
формула площади правильного многоугольника радиус вписанной окружности
формула площади правильного многоугольника радиус описанной окружности
пример задачи

Формула площади правильного многоугольника через длину стороны и число сторон

S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}

a – длина стороны многоугольника

n – число сторон многоугольника

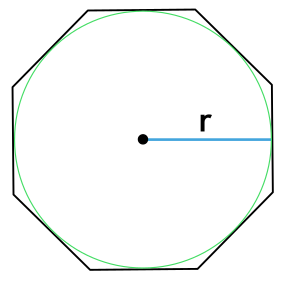
Формула площади правильного многоугольника через радиус вписанной окружности

S = nr^2 tg dfrac{180°}{n}

r – радиус вписанной в многоугольник окружности

n – число сторон многоугольника

Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}

R – радиус описанной в многоугольник окружности

n – число сторон многоугольника

Пример задачи на нахождение площади правильного многоугольника

Задача 1

Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r – радиус вписанной окружности.

Решение

Чтобы решить эту задачу мы используем вторую формулу.

S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2

Ответ: 486 cdot tg 30° approx 280.59223 : см^2

Чтобы проверить ответ воспользуемся калькулятором .

Источник

В данной статье речь пойдёт о том, как выразить площадь многоугольника, в который можно вписать окружность, через радиус этой окружности. Сразу стоит отметить, что не во всякий многоугольник можно вписать окружность. Однако, если это возможно, то формула, по которой вычисляется площадь такого многоугольника, становится очень простой. Дочитайте эту статью до конца или посмотрите прилагающийся видеоурок, и вы узнаете, как же выразить площадь многоугольника через радиус вписанной в него окружности.

Формула площади многоугольника через радиус вписанной окружности

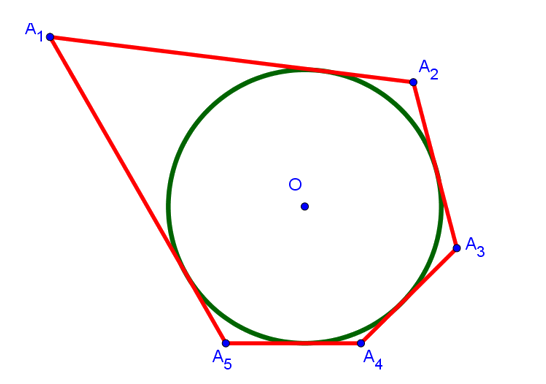
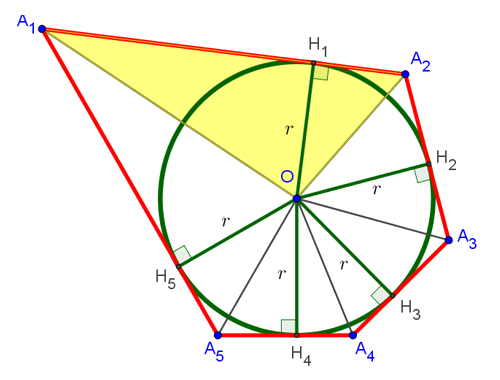
Нарисуем многоугольник A₁A₂A₃A₄A₅, не обязательно правильный, но такой, в который можно вписать окружность. Напомню, что вписанной называется окружность, которая касается всех сторон многоугольника. На рисунке это зелёная окружность с центром в точке O:

Мы взяли здесь для примера 5-угольник. Но на самом деле это не имеет существенного значения, поскольку дальнейшее доказательство справедливо и для 6-угольника и для 8-угольника и вообще для любого сколь угодно «угольника».

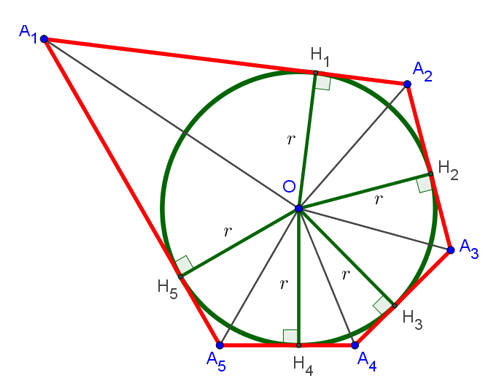
Если соединить центр вписанной окружности со всеми вершинами многоугольника, то он разобьётся на столько треугольников, сколько вершин в данном многоугольнике. В нашем случае: на 5 треугольников. Если же соединить точку O со всеми точками касания вписанной окружности со сторонами многоугольника, то получится 5 отрезков (на рисунке снизу это отрезки OH₁, OH₂, OH₃, OH₄ и OH₅), которые равны радиусу окружности и перпендикулярны сторонам многоугольника, к которым они проведены. Последнее справедливо, поскольку радиус, проведенный в точку касания, перпендикулярен касательной:

Как же найти площадь нашего описанного многоугольника? Ответ прост. Нужно сложить площади всех полученных в результате разбиения треугольников:

$[ S = S_{OA_1A_2}+S_{OA_2A_3}+S_{OA_3A_4}+S_{OA_4A_5}+S_{OA_5A_1}. ]$

Рассмотрим, чему равна площадь треугольника $S_{OA_1A_2}$ . На рисунке снизу он выделен жёлтым цветом:

Она равна половине произведения основания A₁A₂ на высоту OH₁, проведённую к этому основанию. Но, как мы уже выяснили, эта высота равна радиусу вписанной окружности. То есть формула площади треугольника принимает вид: $S=frac{1}{2}rcdot A_1A_2$ , где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:

$[ S = frac{1}{2}rcdot A_1A_2 + frac{1}{2}rcdot A_2A_3+ ]$

$[ +frac{1}{2}rcdot A_3A_4+frac{1}{2}rcdot A_4A_5+frac{1}{2}rcdot A_5A_1. ]$

Видно, что во всех слагаемых этой суммы ест общий множитель $frac{1}{2}r$ , который можно вынести за скобки. В результате получится вот такое выражение:

$[ S = frac{1}{2}rleft(A_1A_2 +A_2A_3 +A_3A_4 +A_4A_5 +A_5A_1right). ]$

То есть в скобках осталась просто сумма всех сторон многоугольника, то есть его периметр P. Чаще всего в этой формуле выражение $frac{1}{2}P$ заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:

То есть площадь многоугольника, в который вписана окружность известного радиуса, равна произведению этого радиуса на полупериметр многоугольника. Это и есть тот результат, в которому мы стремились.

Отметит напоследок, что в треугольник, который является частным случаем многоугольника, всегда можно вписать окружность. Поэтому для треугольника эту формулу можно применять всегда. Для остальных многоугольников, с количеством сторон большим 3, сперва нужно убедиться, что в них можно вписать окружность. Если это так, можно смело использовать эту простую формулу и находить по ней площадь этого многоугольника.

Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич

Источник

Найдём площадь правильного многоугольника через радиусы вписанной и описанной окружностей и через его сторону.

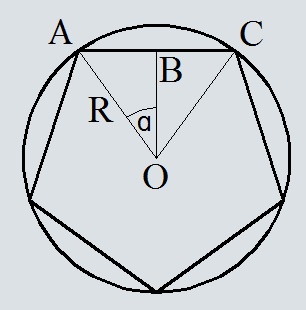
Любой правильный многоугольник вписан в окружность и описан около окружности. Центры вписанной и описанной окружностей совпадают и называются центром правильного многоугольника.

Соединив центр правильного n-угольника

$[{A_1}{A_2}{A_3}{A_4}...{A_{n - 1}}{A_n}]$

со всеми его вершинами, получим n равнобедренных треугольников.

Основание каждого такого треугольника равно стороне многоугольника, боковые стороны равны радиусу описанной около многоугольника окружности угол при вершине — центральному углу правильного многоугольника

$[{A_1}{A_2} = a,]$

$[O{A_1} = O{A_2} = R,]$

$[angle {A_1}O{A_2} = frac{{{{360}^o}}}{n}]$

Так как площадь треугольника равна половине произведения его сторон на синус угла между ними,

$[{S_{Delta {A_1}O{A_2}}} = frac{1}{2} cdot {A_1}O cdot {A_2}O cdot sin angle {A_1}O{A_2}.]$

Отсюда

$[{S_{Delta {A_1}O{A_2}}} = frac{1}{2} cdot {R^2} cdot sin frac{{{{360}^o}}}{n}.]$

Поскольку многоугольник состоит из n таких треугольников, формула площади правильного многоугольника через радиус описанной окружности:

$[S = frac{1}{2} cdot {R^2} cdot n cdot sin frac{{{{360}^o}}}{n}.]$

Проведём в треугольнике A1OA2 высоту OF. Её длина равна радиусу вписанной в правильный n-угольник окружности:

По свойству равнобедренного треугольника OF является также его биссектрисой и медианой:

$[angle {A_1}OF = frac{1}{2}angle {A_1}O{A_2} = frac{1}{2} cdot frac{{{{360}^o}}}{n} = frac{{{{180}^o}}}{n},]$

$[{A_1}F = frac{1}{2}{A_1}{A_2}.]$

Из прямоугольного треугольника A1OF по определению тангенса

$[tgangle {A_1}OF = frac{{{A_1}F}}{{OF}},]$

откуда

$[{A_1}F = OF cdot tgangle {A_1}OF = r cdot tgfrac{{{{180}^o}}}{n}.]$

Так как площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне,

$[{S_{Delta {A_1}O{A_2}}} = frac{1}{2} cdot {A_1}{A_2} cdot OF = {A_1}Fcdot OF,]$

$[{S_{Delta {A_1}O{A_2}}} = r cdot tgfrac{{{{180}^o}}}{n} cdot r = {r^2} cdot tgfrac{{{{180}^o}}}{n}.]$

Площадь

$[{A_1}{A_2}{A_3}{A_4}...{A_{n - 1}}{A_n}]$

равна сумме n таких площадей.

Таким образом, формула площади правильного многоугольника через радиус вписанной окружности:

$[S = {r^2} cdot n cdot tgfrac{{{{180}^o}}}{n}.]$

Из треугольника A1OF

$[OF = frac{{{A_1}F}}{{tgangle {A_1}OF}} = frac{{frac{1}{2}{A_1}{A_2}}}{{tgangle {A_1}OF}} = frac{a}{{2tgfrac{{{{180}^o}}}{n}}}.]$

Следовательно,

$[{S_{Delta {A_1}O{A_2}}} = {A_1}F cdot OF = frac{1}{2}a cdot frac{a}{{2tgfrac{{{{180}^o}}}{n}}} = frac{{{a^2}}}{{4tgfrac{{{{180}^o}}}{n}}}.]$

Поскольку многоугольник состоит из n равных треугольников, формула площади правильного многоугольника через его сторону:

$[S = frac{{{a^2} cdot n}}{{4tgfrac{{{{180}^o}}}{n}}}.]$

Источник

Площадь правильного многоугольника по радиусу описанной окружности и количеству сторон

Калькулятор рассчитывает площадь правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон.

Введите радиус описанной окружности R

Введите количество сторон многоугольника n

Формула площади правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон

Где R – радиус описанной около правильного многоугольника окружности,
n – количество сторон правильного многоугольника

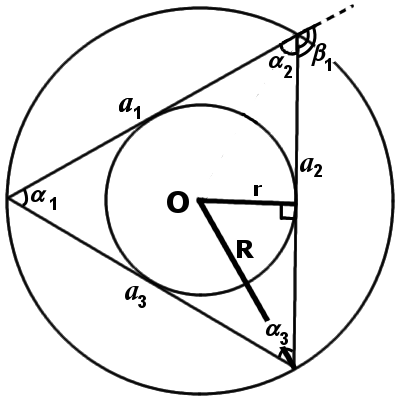
Вывод формулы площади правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон

Треугольники AOB и COB равны и являются прямоугольными.

AO=OC=R.

Угол α будет равен 360 градусов/(количество сторон * 2)

Площадь треугольника ACO будет равно произведению половины основания AC=2×AB на высоту BO

Затем умножим площадь треугольника ACO на количество сторон правильного многоугольника и получим площадь правильного многоугольника

Заменим sin(2α)=2sin(α)cos(α) и подставим вместо α ранее выведенную формулу

Похожие калькуляторы

Источник

Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника

Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

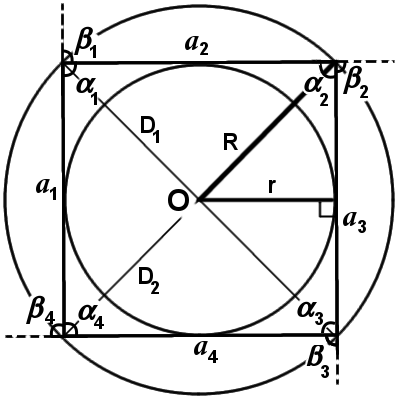
Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие:

Все стороны и углы одинаковы:

a₁ = a₂ = a₃ = … = a_n-1 = a_n

α₁ = α₂ = α₃ = … = α_n-1 = α_n

Основные свойства правильного многоугольника

1. Все стороны равны:

a₁ = a₂ = a₃ = … = a_n-1 = a_n

2. Все углы равны:

α₁ = α₂ = α₃ = … = α_n-1 = α_n

3. Центр вписанной окружности O_в совпадает з центром описанной окружности O_о, что и образуют центр многоугольника O

4. Сумма всех углов n-угольника равна:

180° · (n – 2)

5. Сумма всех внешних углов n-угольника равна 360°:

β₁ + β₂ + β₃ + … + β_n-1 + β_n = 360°

6. Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:

7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:

8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O

Правильный n-угольник – формулы

Формулы длины стороны правильного n-угольника

1. Формула стороны правильного n-угольника через радиус вписанной окружности:

2. Формула стороны правильного n-угольника через радиус описанной окружности:

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны:

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны:

Формулы площади правильного n-угольника

1. Формула площади n-угольника через длину стороны:

2. Формула площади n-угольника через радиус вписанной окружности:

3. Формула площади n-угольника через радиус описанной окружности:

Формула периметра правильного многоугольника:

Формула периметра правильного n-угольника:

P = na

Формула определения угла между сторонами правильного многоугольника:

Формула угла между сторонами правильного n-угольника:

Изображение правильного треугольника с обозначениями

Рис.3

Правильный треугольник

Формулы правильного треугольника:

1. Формула стороны правильного треугольника через радиус вписанной окружности:

a = 2r √3

2. Формула стороны правильного треугольника через радиус описанной окружности:

a = R√3

3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:

4. Формула радиуса описанной окружности правильного треугольника через длину стороны:

5. Формула площади правильного треугольника через длину стороны:

6. Формула площади правильного треугольника через радиус вписанной окружности:

S = r² 3√3

7. Формула площади правильного треугольника через радиус описанной окружности:

8. Угол между сторонами правильного треугольника:

α = 60°

Изображение правильного четырехугольнику с обозначениями

Рис.4

Правильный четырехугольник

Правильный четырехугольнику – квадрат.

Формулы правильного четырехугольника:

1. Формула стороны правильного четырехугольника через радиус вписанной окружности:

a = 2r

2. Формула стороны правильного четырехугольника через радиус описанной окружности:

a = R√2

3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:

4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:

5. Формула площади правильного четырехугольника через длину стороны:

S = a²

6. Формула площади правильного четырехугольника через радиус вписанной окружности:

S = 4 r²

7. Формула площади правильного четырехугольника через радиус описанной окружности:

S = 2 R²

8. Угол между сторонами правильного четырехугольника:

α = 90°

Правильный шестиугольник

Формулы правильного шестиугольника:

1. Формула стороны правильного шестиугольника через радиус вписанной окружности:

2. Формула стороны правильного шестиугольника через радиус описанной окружности:

a = R

3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:

4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:

R = a

5. Формула площади правильного шестиугольника через длину стороны:

6. Формула площади правильного шестиугольника через радиус вписанной окружности:

S = r² 2√3

7. Формула площади правильного шестиугольника через радиус описанной окружности:

8. Угол между сторонами правильного шестиугольника:

α = 120°

Правильный восьмиугольник

Формулы правильного восьмиугольника:

1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:

a = 2r · (√2 – 1)

2. Формула стороны правильного восьмиугольника через радиус описанной окружности:

a = R√2 – √2

3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:

4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:

5. Формула площади правильного восьмиугольника через длину стороны:

S = a² 2(√2 + 1)

6. Формула площади правильного восьмиугольника через радиус вписанной окружности:

S = r² 8(√2 – 1)

7. Формула площади правильного восьмиугольника через радиус описанной окружности:

S = R² 2√2

8. Угол между сторонами правильного восьмиугольника:

α = 135°

Источник

Содержание:

Формула площади правильного многоугольника через длину стороны и число сторон

Формула площади правильного многоугольника через радиус вписанной окружности

Формула площади правильного многоугольника через радиус описанной окружности

Пример задачи на нахождение площади правильного многоугольника

Формула площади многоугольника через радиус вписанной окружности

Площадь правильного многоугольника по радиусу описанной окружности и количеству сторон

Формула площади правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон

Вывод формулы площади правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон

Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника

Признаки правильного многоугольника

Основные свойства правильного многоугольника

Правильный n-угольник – формулы

Формулы длины стороны правильного n-угольника

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса описанной окружности правильного n-угольника

Формулы площади правильного n-угольника

Формула периметра правильного многоугольника:

Формула определения угла между сторонами правильного многоугольника:

Правильный треугольник

Формулы правильного треугольника:

Правильный четырехугольник

Формулы правильного четырехугольника:

Правильный шестиугольник

Формулы правильного шестиугольника:

Правильный восьмиугольник

Формулы правильного восьмиугольника:

Вам также может понравиться

Ошибка 80040218 как исправить

Как найти захоронение по номеру захоронения

Как найти сколько градусов составляет угол

Добавить комментарий Отменить ответ