В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
-
2. Площадь правильной треугольной пирамиды
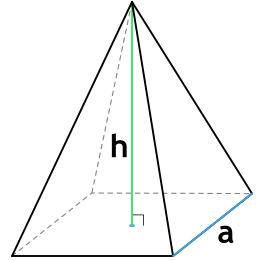
- 3. Площадь правильной четырехугольной пирамиды
- 4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
1. Общая формула
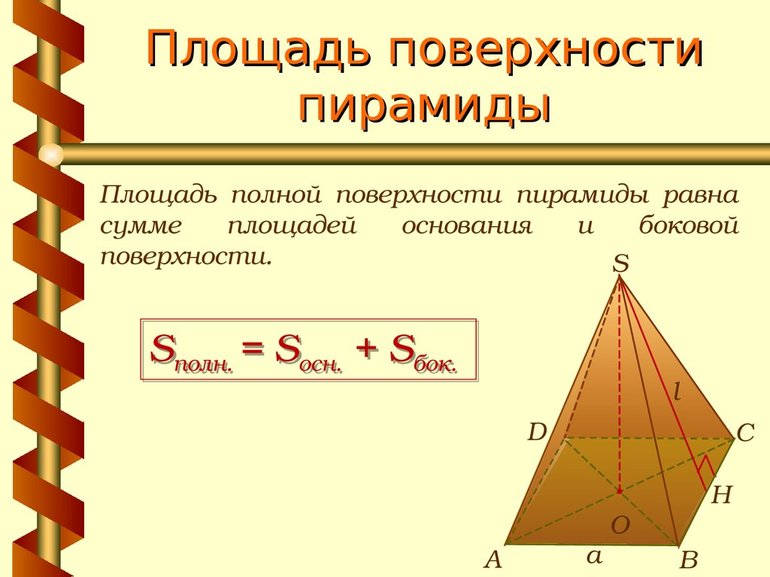
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
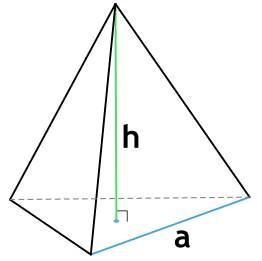
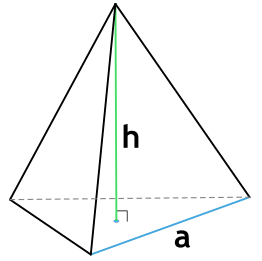
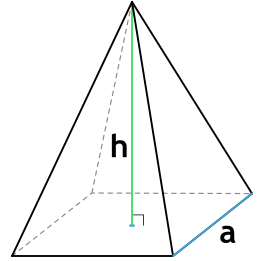
1. Через длину основания (a) и высоту (h):
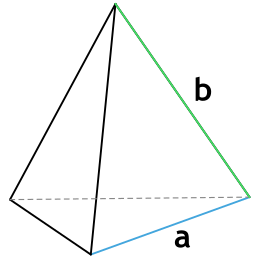
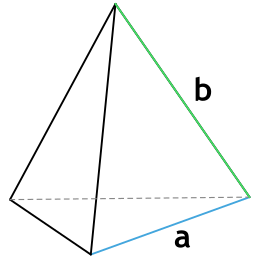
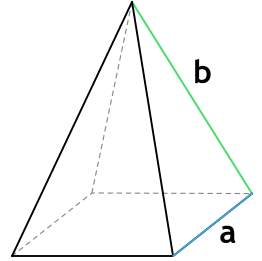
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
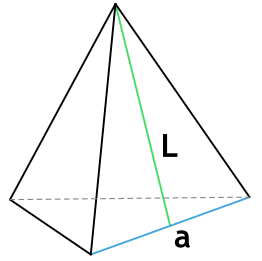
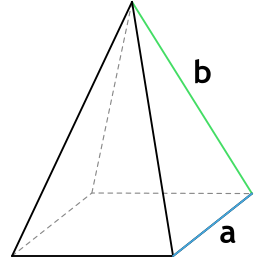
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
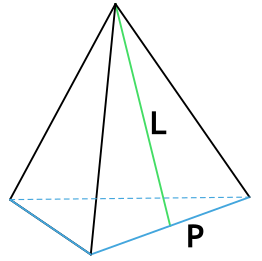
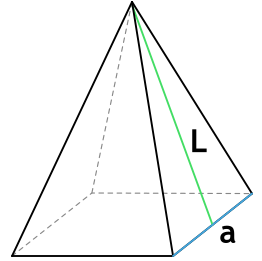
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
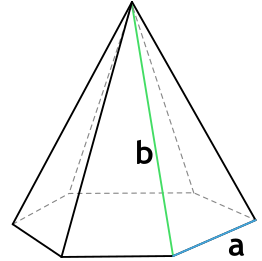
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник
Пирамида — это многогранник, в основании которого лежит многоугольник, а грани его являются треугольниками.
Онлайн-калькулятор площади поверхности пирамиды
Стоит остановиться на определении некоторых составляющих пирамиды.
У нее, как и у других многогранников, есть ребра. Они сходятся к одной точке, которая называется вершиной пирамиды. В ее основании может лежать произвольный многоугольник. Гранью называется геометрическая фигура, образованная одной из сторон основания и двумя ближайшими ребрами. В нашем случае это треугольник. Высотой пирамиды называется расстояние от плоскости, в которой лежит ее основание, до вершины многогранника. Для правильной пирамиды существует еще понятие апофемы – это перпендикуляр, опущенный из вершины пирамиды к её основанию.
Виды пирамид
Существуют 3 вида пирамид:
- Прямоугольная — та, у которой какое-либо ребро образует прямой угол с основанием.
- Правильная — у нее основание – правильная геометрическая фигура, а вершина самого многоугольника является проекцией центра основания.
- Тетраэдр — пирамида, составленная из треугольников. Причем каждый из них может быть принят за основание.
Формула площади поверхности пирамиды
Для нахождения полной площади поверхности пирамиды нужно сложить площадь боковой поверхности и площадь основания.
Самой простой является случай правильной пирамиды, поэтому нею мы и займемся. Вычислим полную площадь поверхности такой пирамиды. Площадь боковой поверхности равна:
Sбок=12⋅l⋅pS_{text{бок}}=frac{1}{2}cdot lcdot p
ll — апофема пирамиды;
pp — периметр основания пирамиды.
Полная площадь поверхности пирамиды:
S=Sбок+SоснS=S_{text{бок}}+S_{text{осн}}
SбокS_{text{бок}} — площадь боковой поверхности пирамиды;
SоснS_{text{осн}} — площадь основания пирамиды.
Пример решения задачи.
Найти полную площадь треугольной пирамиды, если её апофема равна 8 (см.), а в основании лежит равносторонний треугольник со стороной 3 (см.)
Решение
l=8l=8
a=3a=3
Найдем периметр основания. Так как в основании лежит равносторонний треугольник со стороной aa, то его периметр pp (сумма всех его сторон):
p=a+a+a=3⋅a=3⋅3=9p=a+a+a=3cdot a=3cdot 3=9
Тогда боковая площадь пирамиды:
Sбок=12⋅l⋅p=12⋅8⋅9=36S_{text{бок}}=frac{1}{2}cdot lcdot p=frac{1}{2}cdot 8cdot 9=36 (см. кв.)
Теперь найдем площадь основания пирамиды, то есть площадь треугольника. В нашем случае треугольник равносторонний и его площадь можно вычислить по формуле:
Sосн=3⋅a24S_{text{осн}}=frac{sqrt{3}cdot a^2}{4}
aa — сторона треугольника.
Получаем:
Sосн=3⋅a24=3⋅324≈3.9S_{text{осн}}=frac{sqrt{3}cdot a^2}{4}=frac{sqrt{3}cdot 3^2}{4}approx3.9 (см. кв.)
Полная площадь:
S=Sбок+Sосн≈36+3.9=39.9S=S_{text{бок}}+S_{text{осн}}approx36+3.9=39.9 (см. кв.)
Ответ: 39.9 см. кв.
Еще один пример, немного сложнее.
Основанием пирамиды является квадрат с площадью 36 (см. кв.). Апофема многогранника в 3 раза больше стороны основания aa. Найти полную площадь поверхности данной фигуры.
Решение
Sквад=36S_{text{квад}}=36
l=3⋅al=3cdot a
Найдем сторону основания, то есть сторону квадрата. Его площадь и длина стороны связанны:
Sквад=a2S_{text{квад}}=a^2
36=a236=a^2
a=6a=6
Найдем периметр основания пирамиды (то есть, периметр квадрата):
p=a+a+a+a=4⋅a=4⋅6=24p=a+a+a+a=4cdot a=4cdot 6=24
Найдем длину апофемы:
l=3⋅a=3⋅6=18l=3cdot a=3cdot 6=18
В нашем случае:
Sквад=SоснS_{text{квад}}=S_{text{осн}}
Осталось найти только площадь боковой поверхности. По формуле:
Sбок=12⋅l⋅p=12⋅18⋅24=216S_{text{бок}}=frac{1}{2}cdot lcdot p=frac{1}{2}cdot 18cdot 24=216 (см. кв.)
Полная площадь:
S=Sбок+Sосн=216+36=252S=S_{text{бок}}+S_{text{осн}}=216+36=252 (см. кв.)
Ответ: 252 см. кв.
Возникают трудности с тем, чтобы найти площадь поверхности пирамиды? У нас вы можете заказать контрольную работу по геометрии!
Как найти площадь поверхности пирамиды
На данной странице калькулятор поможет рассчитать площадь поверхности пирамиды онлайн. Для расчета задайте площадь основания и апофему.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Апофема – опущенный перпендикуляр из вершины на ребро основания.
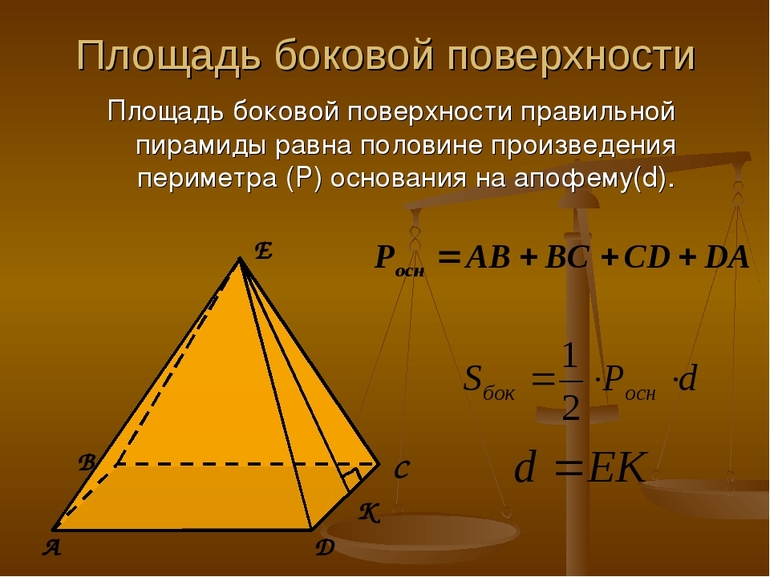
Боковая поверхность через периметр и апофему
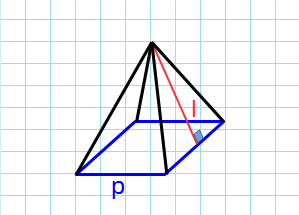
Формула площади боковой поверхности правильной пирамиды через периметр и апофему:
p – периметр основания пирамиды; l – апофема пирамиды.
Боковая поверхность через высоту и сторону основания
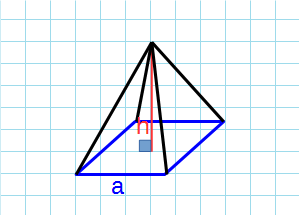
Формула площади боковой поверхности правильной пирамиды через высоту и сторону основания:
a – сторона основания; h – высота пирамиды; n – число сторон в основании.
Полная поверхность через высоту и сторону основания

Формула площади полной поверхности правильной пирамиды через высоту и сторону основания:
a – сторона основания; h – высота пирамиды; n – число сторон в основании.
Полная площадь тетраэдра
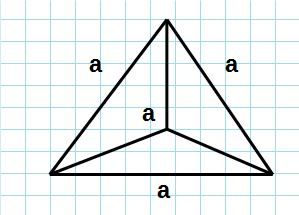
Формула полной площадь тетраэдра:
a – сторона основания.

{S_{полн} = dfrac{1}{2}PL + S}
На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды – это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды – это совокупная площадь всех боковых граней пирамиды.
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
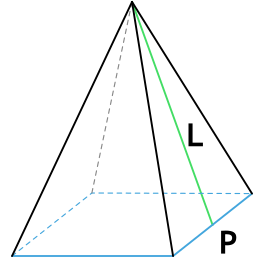
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
{S_{полн} = dfrac{1}{2}PL+S}
P – периметр основания пирамиды
L – апофема пирамиды
S – площадь основания пирамиды
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{na}{2} {Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} + sqrt{h^2+ Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
n – число сторон основания
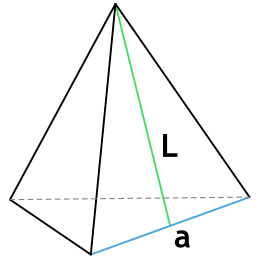
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{a^2 sqrt{3}+6aL}{4}}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{a^2 sqrt{3}+6a sqrt{b^2 – dfrac{a^2}{4}}}{4}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{3a}{2} {Bigg( dfrac{a}{2 tg ( 60°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{полн} = 2a {Bigg( dfrac{a}{2 tg ( 45°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{полн} = a^2+2aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3asqrt{b^2-dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{полн} = 3a {Bigg( dfrac{a}{2 tg ( 30°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
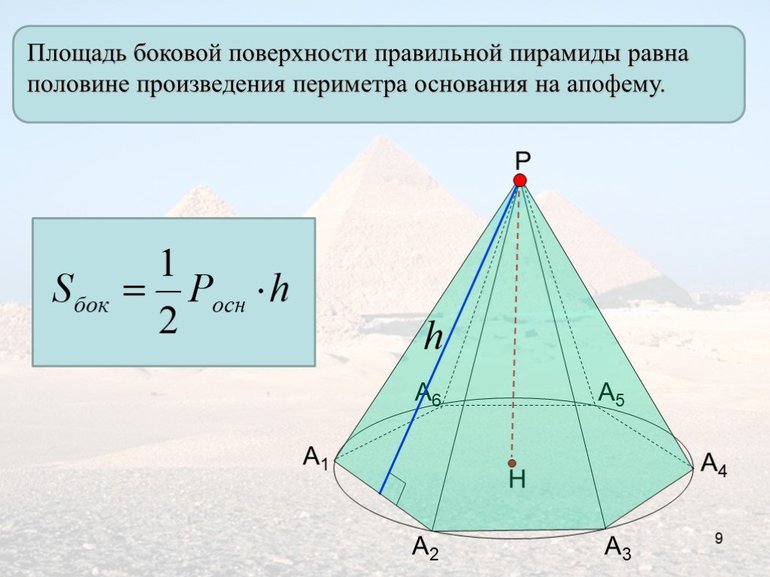
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
{S_{бок} = dfrac{1}{2}PL}
P – периметр основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{na}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( dfrac{180°}{n})} Bigg) ^2} }
a – сторона основания пирамиды
h – высота пирамиды
n – число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{бок} = dfrac{3}{2}aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{бок} = dfrac{3a sqrt{b^2 – dfrac{a^2}{4}}}{2}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{3a}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
{S_{бок} =dfrac{1}{2}PL}
P – периметр основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{бок} = 2aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 2a sqrt{b^2 – dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{бок} = 3aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 3asqrt{b^2-dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{бок} = 3a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. Найдите площадь поверхности этой пирамиды.
Решение
Так как пирамида правильная четырехугольная, то воспользуемся соответствующей формулой площади поверхности через сторону основания и боковую грань.
S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}} = 60^2 + 2 cdot 60 sqrt{78^2- dfrac{60^2}{4}} = 3600 + 120 sqrt{6084- dfrac{3600}{4}} = 3600 + 120 sqrt{6084 – 900} = 3600 + 120 sqrt{5184} = 3600 + 120 cdot 72 = 3600 + 8640 = 12240 : см²
Ответ: 12240 см²
Проверим полученный ответ с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной треугольной пирамиды со стороной 6см и апофемой 10см.
Решение
Из условия мы знаем апофему и сторону правильной треугольной пирамиды, поэтому нам потребуется эта формула.
S_{бок} = dfrac{3}{2}aL = dfrac{3}{2} cdot 6 cdot 10 = dfrac{3}{2} cdot 60 = 90 : см²
Ответ: 90 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной четырехугольной пирамиды сторона основания 6см и высота 4см.
Решение
Подставим значения в формулу и произведем расчет.
S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} = 2 cdot 6 sqrt{4^2+ Bigg( dfrac{6}{2 tg ( 45°)} Bigg) ^2} = 60 : см²
Ответ: 60 см²
Проверка .
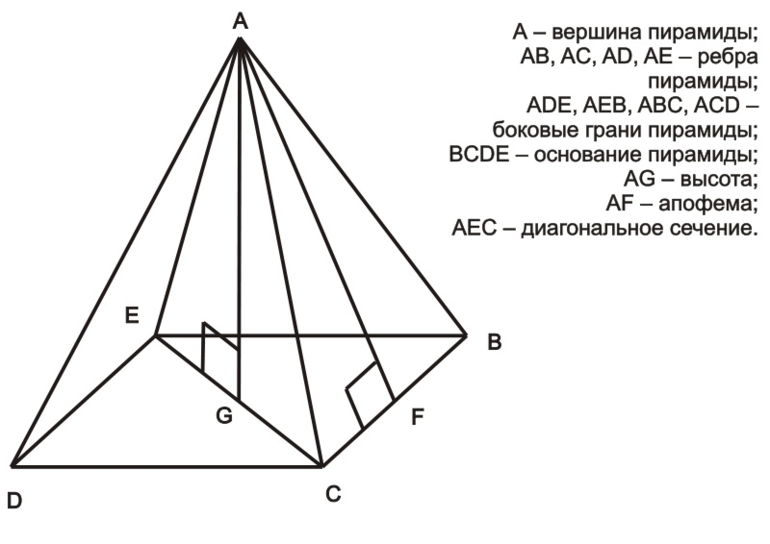
Описание фигуры
С древнегреческого языка пирамида переводится, как многогранник с несколькими гранями — боковыми и основанием. Первые имеют вид треугольников с одной вершиной. С учётом количества углов фигура делится на треугольную (тетраэдр), четырёхугольную, пятиугольную, шестиугольную, n-угольную. Элементы многогранника:
- Апофема или высота. Проводится из вершины боковой грани (БГ).
- БГ. Формируют треугольники с одной вершиной.
- Боковые рёбра (БР). Являются общими сторонами БГ.
- Вершина или точка. Соединяет БР, не принадлежит плоскости, в которой находится основание.
- Высота или часть перпендикуляра. Элемент проведён через вершину к основанию. Чтобы найти высоту, измеряется отрезок между вершинами и нижней стороной фигуры.
- Диагональное сечение. Пересекает диагональ и вершину нижней части фигуры.
- Основание либо многоугольник. На данной поверхности не лежат вершины.
Развертка — плоская фигура, образованная путём совмещения поверхности тела с плоскостью. Грани и другие элементы не накладываются друг на друга. Развёртка поверхности похожа на гибкую плёнку. По факту, это пятиугольная пирамида с равными сторонами и углами. В плоскости она напоминает звезду.
Свойства и теоремы
Для фигуры характерны некоторые свойства. БР одинаковы, если нижняя сторона вписывается в сферу либо окружность так, что вершина приходится на центр. Другие особенности фигуры:
- Боковые рёбра и плоскость нижней стороны формируют равные углы.
- Если БР образуют с плоскостью одинаковые углы либо вблизи основания описывается окружность с вершиной в её центре, тогда все БР одинаковые.
- Если грани наклонены к плоскости основания под определённым углом, тогда площадь боковой поверхности (БП) пирамиды равна ½ произведения периметра нижней стороны на высоту грани.
При решении задач на сайтах онлайн либо из учебников по геометрии используются теоремы, которые связывают пирамиду с иными телами.
Для расчета нужной величины применяется калькулятор, подходящая формула, свойства многогранников. Учёные доказали, что вокруг пирамиды можно описать сферу, если в основании находится многоугольник с окружностью.
Центр сферы — точка, в которой пересекаются плоскости, проходящие через центральную часть ребер. Из теоремы вытекает, что около прямоугольной, квадратной и правильной пирамиды возможно описать сферу. В фигуру вписывается сфера, если биссекторные плоскости двугранных внутренних углов пересекаются в единой точке. Согласно другой теореме, конус вписан в пирамиду, если их вершины совпадают. Основание фигур и апофемы совпадают. Конус описывается вокруг пирамиды, если БР последней фигуры одинаковые.
Цилиндр находится внутри многоугольника, если любое его основание совмещено с окружностью. Цилиндр описан около пирамиды, если вершина последней фигуры находится на одном из его оснований. Другая его нижняя часть описана внизу пирамиды. Подобное действие возможно, если в основании пирамиды вписан многоугольник.
Для правильной пирамиды (нижняя сторона представлена в виде правильного многоугольника с вершиной в центре) характерны некоторые свойства: равенство БР, гранями являются равнобедренные конгруэнтные (равные) треугольники, внутрь и вокруг легко описывается и вписывается сфера. В последнем случае, когда центры сфер совпадают, сумма плоских углов равняется числу пи, а каждый — π/n, где n — количество сторон фигуры в основании.
Пирамида считается прямоугольной, если одно БР перпендикулярно нижней стороне. В таком случае ребро является высотой. В тетраэдре либо треугольной пирамиде любая грань принимается в качестве основания.
Практические задания
На ЕГЭ выпускники решают задачи с объёмом и площадью куба, правильного многоугольника. Фигуры размещены на плоскости либо в системе координат. Основные формулы, которые применяются для вычисления показателей:
- Площадь (S) пирамиды с четырьмя углами и сторонами. Для её расчета потребуется суммировать площади нижних сторон (квадрат и 4 треугольника).
- Общая S: S основания+S боковой поверхности.
- Площадь боковой поверхности пирамиды: S бок. пов.=½Pосн.d.
- Площадь полной поверхности пирамиды. Для её вычисления понадобится суммировать площади БП и основания.
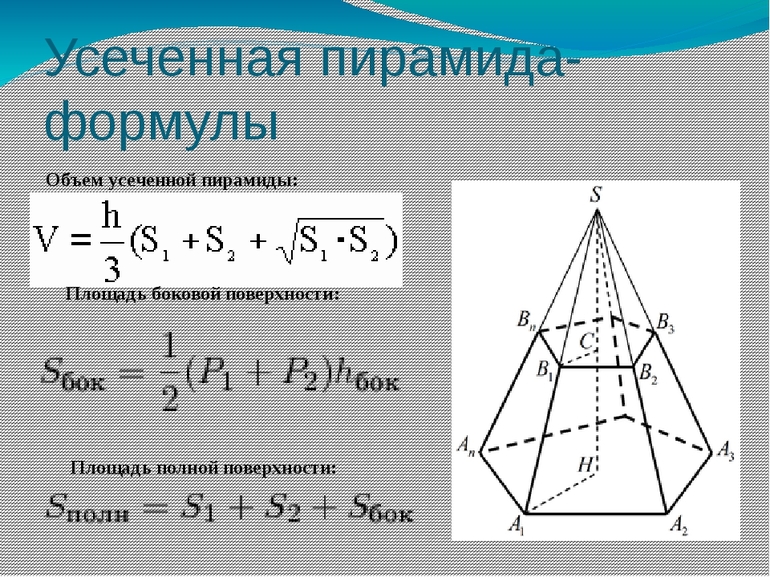
- Площадь усеченной пирамиды: S1+S2+Sбок, где первые два показателя характерны для оснований, в последний для боковой поверхности.
- Объём пирамиды: V=1/3Sосн.H.
Задача 1. Дан четырёхугольный многогранник с равными сторонами в 72 и боковыми ребрами — по 164. Нужно найти площадь четырехугольной пирамиды.
Решение: Так как S=Sбок+Sосн, подставив данные в формулу, получается 4S+a ². Так как Sбок состоит из 4-х одинаковых по площади треугольников, а основание представлено в виде квадрата, поэтому для нахождения площади Sбок используется формула Герона: S=√p (p-a)(p-b)(p-c).
Для вычисления полупериметра потребуется (a+b+c)/2. В формулу поставляются данные. Выходит, что P=(72+164+164)/2=200. Тогда S=√200 (200−72)(200−164)(200−164)=√200х128х36х36=√100х256х36х36=10х16х6х6х=5760. Подставив данные в формулу, находится площадь: S=4х5760+72х72=28224.
Задача 2. Стороны нижней части в шестиугольном многоугольнике равняются 22, а ребра — 61. Нужно найти Sбок. пов.
Решение: Основание фигуры представлено в форме шестиугольника с одинаковыми сторонами. Его площадь соответствует площади шести треугольников. Их стороны равны 61, 61 и 22. Величина вычисляется по формуле S=6S. Чтобы найти S, применяется формула Герона: S=√p (p-a)(p-b)(p-c). Полупериметр равен (a+b+c)/2.
Р=(61+61+22)/2=72. S=√72 (72−61)(72−61)(72−22)=√72х9х9х50=√36х2х9х9х2х25=540.
Данные, подставив в Sбок. пов., приведут к результату 3240. В задаче 1 и 2 можно вычислить площадь через апофему.
Задача 3. Необходимо определить S пов. прав. четырёхугольной пирамиды, когда стороны основания равняются 6, а высота — 4.
Решение: Для определения S вычисляются площади БП и основания. Используется формула Sбок +S осн=4S+ a ². S осн равняется 36, так как оно представлено в виде квадрата со сторонами в 6. БП состоит из 4-х граней либо равных треугольников. Для нахождения площади вычисляется основание и высота фигуры:
S=½ah.
Площадь фигуры соответствует половине произведения апофемы и основания. Первый элемент проведён ко второму. Так как известно, что основание равно 6, поэтому находится высота. Если начертить и рассмотреть треугольник, можно заметить, что катет равен 4. Он же является высотой пирамиды. Значение второго катета — 3 (он соответствует ½ ребра основания).
Для вычисления гипотенузы используется теорема Пифагора:
h= √3²+4²=5.
Площадь БП вычисляется следующим образом:
Sбок=4S=4х½х6х5=60.
S=60+36=96.
При решении задач рекомендуется ориентироваться на чертеж, использовать общепринятые теоремы и свойства фигур. Для наглядности фигура размещается в плоскости в нескольких проекциях. В старших классах, чтобы найти объём либо площадь, многогранники отображаются с помощью координат, функций косинуса и синуса.
Последние переменные используются, чтобы найти значение углов, как острых, так и тупых. Через полученное число и дополнительные формулы, аксиомы вычисляется площадь разных составных элементов фигуры.