Как найти площадь молотка

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S
_ABC = S_ABCD : 2

S
_ABC = 20 : 2 = 10 см²

S
_ABC =
S
_ACD = 10 см²

---

Ваши комментарии

Оставить комментарий:

---

Формулы площадей всех основных фигур

1. Формула площади круга через радиус или диаметр

Зная диаметр или радиус круга, можно найти его площадь.

r — радиус круга

D — диаметр

Формула площади круга, (S):

2. Формула расчета площади треугольника

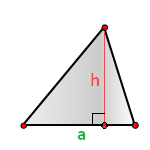
h — высота треугольника

a — основание

Площадь треугольника (S):

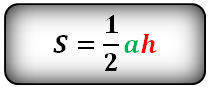
3. Площадь треугольника, формула Герона

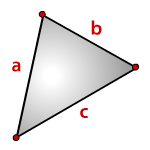
a , b , c , — стороны треугольника

p— полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

4. Площадь прямоугольного треугольника по катетам

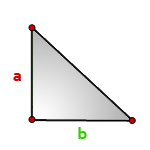
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.

a , b — катеты треугольника

Формула площади прямоугольного треугольника, (S):

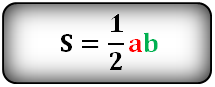
5. Как вычислить площадь равнобедренного треугольника ?

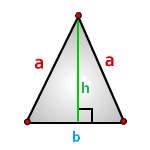
b — основание треугольника

a — равные стороны

h — высота

Формула площади треугольника через высоту h и основание b , ( S ):

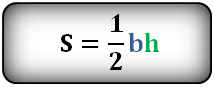
Формула площади треугольника через, стороны a , b , (S):

6. Площадь равностороннего треугольника равна:

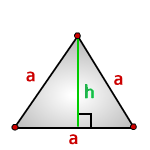
Формулы расчета, площади равностороннего треугольника.

a — сторона треугольника

h — высота

Площадь треугольника только через сторону a , (S):

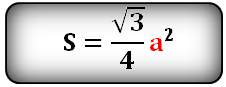
Площадь треугольника только через высоту h , ( S ):

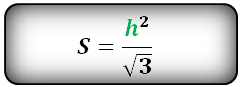
Площадь треугольника через сторону a и высоту h , (S):

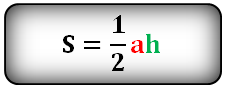
7. Найти площадь треугольника, угол и две стороны

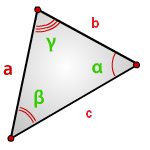
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.

a , b , c — стороны треугольника

α , β , γ — углы

Формулы площади треугольника, через две стороны и угол между ними, ( S ):

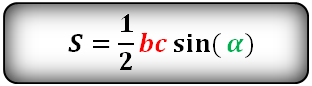
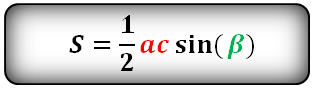
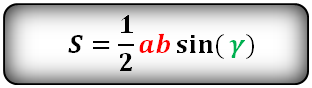
8. Площадь треугольника по стороне и двум углам, формула.

a , b , c — стороны треугольника

α , β , γ — противолежащие углы

Площадь треугольника через сторону и два угла (S):

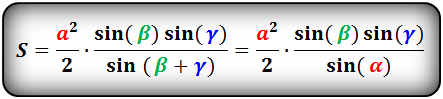
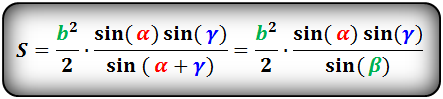
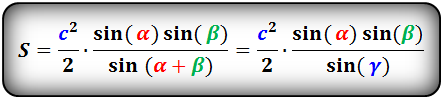
9. Формула расчета площади прямоугольника

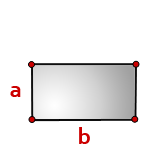
b — длина прямоугольника

a — ширина

Формула площади прямоугольника, (S):

10. Как рассчитать площадь квадрата через диагональ или сторону

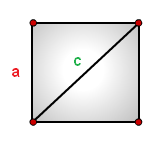
a — сторона квадрата

c — диагональ

Формула площади квадрата через сторону a , (S):

Формула площади квадрата через диагональ c , (S):

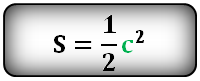
11. Формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

a, b — стороны параллелограмма

α , β — углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

2. Формула площади параллелограмма через сторону и высоту

a, b — стороны параллелограмма

H _b — высота на сторону b

H _a — высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D — большая диагональ

d — меньшая диагональ

α , β — углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , (S):

12. Площадь произвольной трапеции

1. Формула площади трапеции через основания и высоту

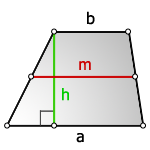
b — верхнее основание

a — нижнее основание

m — средняя линия

h — высота трапеции

Формула площади трапеции, (S):

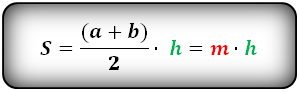
2. Формула площади трапеции через диагонали и угол между ними

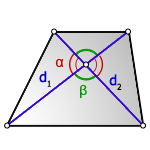
d ₁, d ₂ — диагонали трапеции

α , β — углы между диагоналями

Формула площади трапеции, (S):

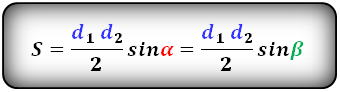
3. Формула площади трапеции через четыре стороны

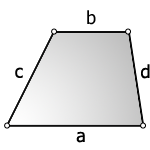
b — верхнее основание

a — нижнее основание

c, d — боковые стороны

Формула площади трапеции, (S):

13. Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α , β — углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α , β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции

c — боковая сторона

α , β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Источник

Площадь фигур

Площадь фигуры является суммарной числовой характеристикой всех единичных квадратных элементов плоскости. В зависимости от размера фигур стороны квадрата единичного элемента могут быть равны 1 мм, см, м, дюйму, км и пр. S фигур могут измеряться в следующих единицах измерения: мм2, см2, м2, гектарах, квадратных километрах и пр.

Вычислить, найти площадь геометрических фигур

Онлайн Расчеты и формулы площади для плоских фигур
Площадь треугольника калькулятор нахождения площади треугольников	Площадь прямоугольного треугольника онлайн формула площади прямоугольного треугольника
Площадь равнобедренного треугольника найти площади равнобедренных треугольников	Площадь равностороннего треугольника вычислить площадь равностороннего треугольника
Площадь треугольника по формуле Герона площадь Герона, формула	Площадь квадрата чему равна площадь квадрата
Площадь прямоугольника как найти чему равна площадь прямоугольника	Площадь круга онлайн калькулятор площади круга через радиуса
Площадь ромба как найти площадь ромба через диагонали и т.д.	Площадь параллелограмма онлайн калькулятор для нахождения площади параллелограмма
Площадь трапеции площадь прямоугольной и равнобедренной трапеции	Площадь эллипса формула площади эллипса онлайн
Площадь кольца как вычислить площадь кольца онлайн	Площадь четырехугольника чему равна площадь четырехугольника, формула
Площадь сектора кольца подсчитать площади сектора кольца	Площадь сектора круга получить площадь сектора круга
Площадь сегмента круга решить площадь сегмента круга
Онлайн Расчеты и формулы площади для объемных фигур
Площадь шара калькулятор нахождения площадь поверхности сферы или шара	Площадь куба как найти чему равна площадь поверхности куба
Площадь цилиндра калькулятор для нахождения площади поверхности и основания цилиндра	Площадь пирамиды формулы расчета площади боковой поверхности и основания пирамиды
Площадь параллелепипеда калькулятор площади параллелепипеда прямоугольного и др.	Площадь конуса нахождение площади поверхностей конуса
Площадь усеченного конуса калькулятор нахождения площади поверхности усеченного конуса	Площадь тетраэдра площадь поверхности и грани тетраэдра
Площадь призмы калькулятор нахождения площади поверхности и боковой площади призмы

Площадь фигуры сложной формы может составляться из различных элементарных фигур: треугольников, квадратов, прямоугольников и пр. Общая площадь будет высчитываться путем суммирования площадей составляющих компонент.

Набор онлайн-калькуляторов страницы дает возможность оперативного вычисления не только S плоских фигур (квадрата, прямоугольника, круга, ромба, эллипса), но и площадей объемных фигур (куба, призмы, конуса, цилиндра, сферы, тетраэдра и пр.), являющихся совокупностью нескольких плоскостей.

Вычисление площадей фигур востребовано для решения различных задач:
— строительных;
— кадастровых;
— инженерных и пр.

Государство осуществляет кадастровый учет земельных участков, основным учитываемым параметром которых является площадь. Специалистами БТИ фиксируется общая и полезная жилая площадь квартир. В быту иногда нужно вычислять площадь ковра, натяжного потолка, площадь дачного участка и пр.

Источник

Площадь фигуры сложной формы может составляться из различных элементарных фигур: треугольников, квадратов, прямоугольников и пр. Общая площадь будет высчитываться путем суммирования площадей составляющих компонент.

Набор онлайн-калькуляторов страницы дает возможность оперативного вычисления не только S плоских фигур (квадрата, прямоугольника, круга, ромба, эллипса), но и площадей объемных фигур (куба, призмы, конуса, цилиндра, сферы, тетраэдра и пр.), являющихся совокупностью нескольких плоскостей.

Вычисление площадей фигур востребовано для решения различных задач:
– строительных;
– кадастровых;
– инженерных и пр.

Государство осуществляет кадастровый учет земельных участков, основным учитываемым параметром которых является площадь. Специалистами БТИ фиксируется общая и полезная жилая площадь квартир. В быту иногда нужно вычислять площадь ковра, натяжного потолка, площадь дачного участка и пр.

Определения площади поверхностей изделий

Определения площади поверхностей изделий

Вычисления площади поверхностей изделий проводят определением размеров деталей изделий с помощью линейки и штангенциркуля.

Площади поверхности изделий, имеющие простые формы геометрических тел (цилиндр, конус пирамида и. т. д.) определяются по известным из математики формулам.

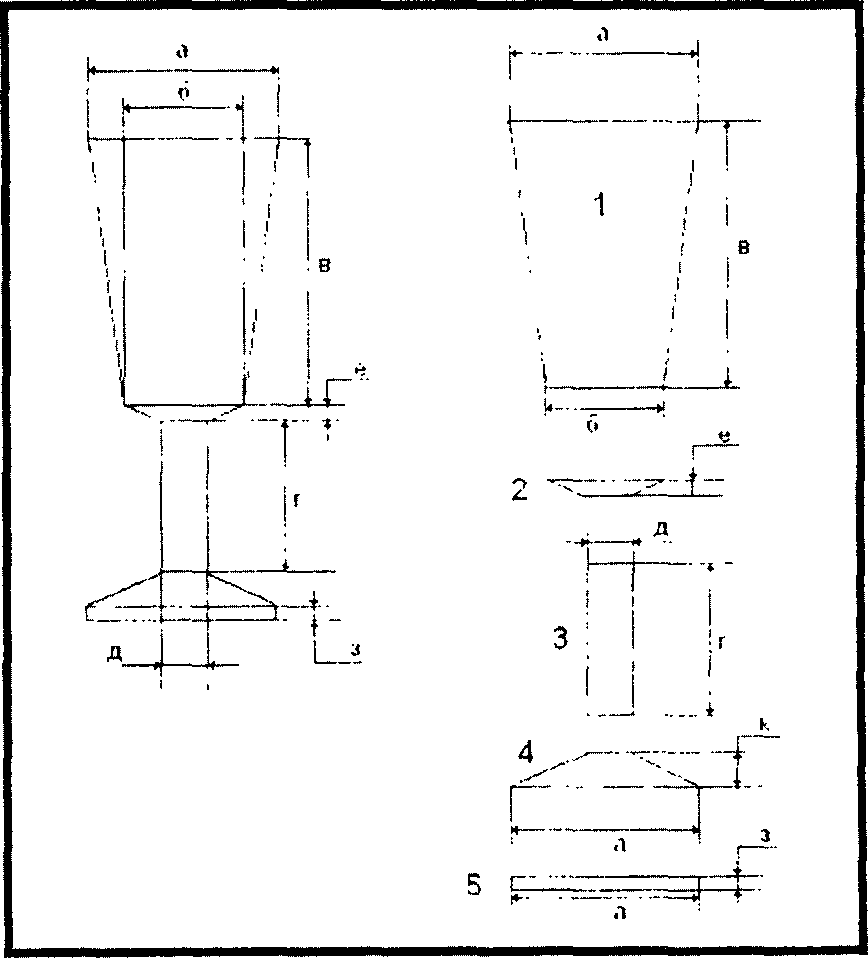
Например, для определения площади поверхности рюмки (рис. 1.1), условно разбиваем ее на простые геометрические фигуры. После подсчетов площадей поверхности фигур полученные величины складываем: S=S

+S:-

-S3+S

-S5.

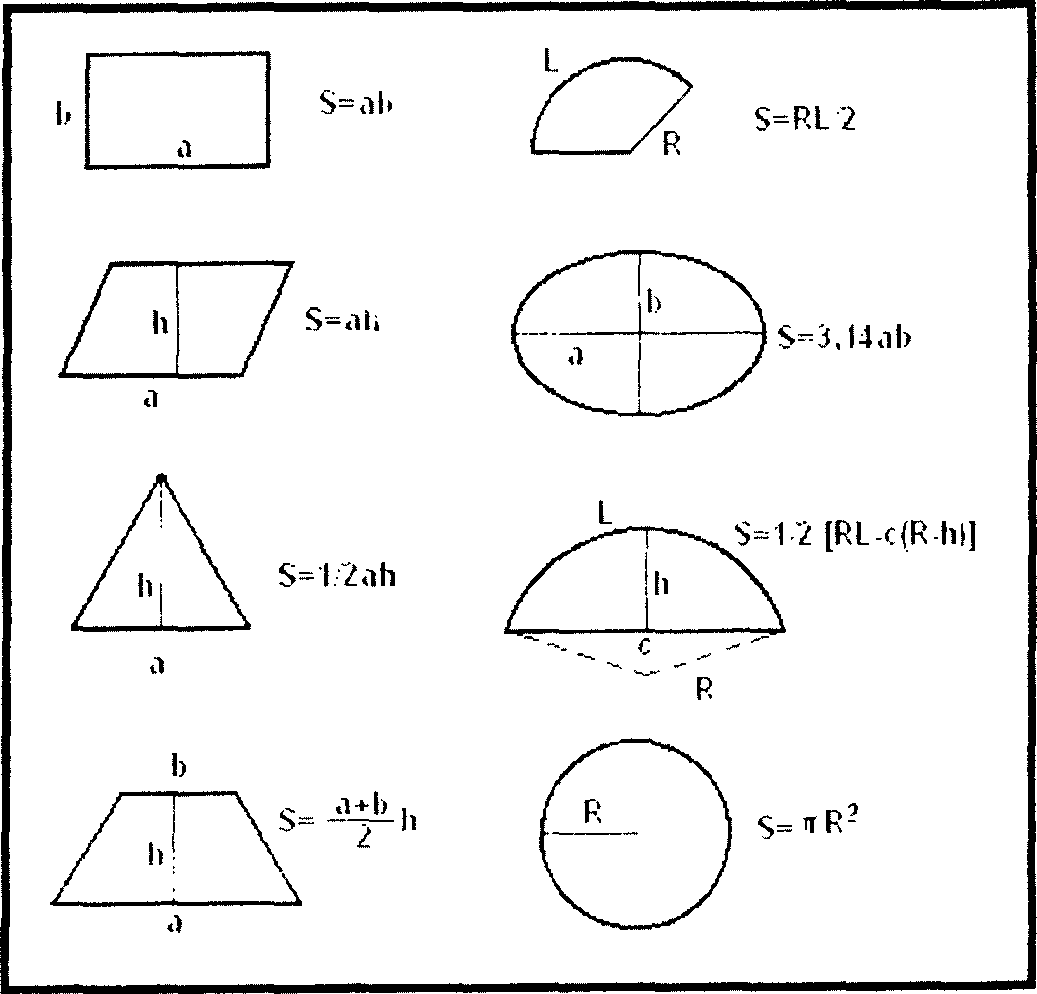
Поверхностями малых участков изделия пренебрегаем. Участки изделий, имеющие неправильные формы (рис. 1.2: 1.3). приближенно приравниваем к более простым фигурам прямом ольнику. конусу призме и т.д.

Полученную величину площади поверхности изделия в мм” надо разделить на 10000, чтобы получить площадь в дм

Рис. 1.1. Схема рюмки и детали рюмки

Рис. 1.2.Площади плоских фигур

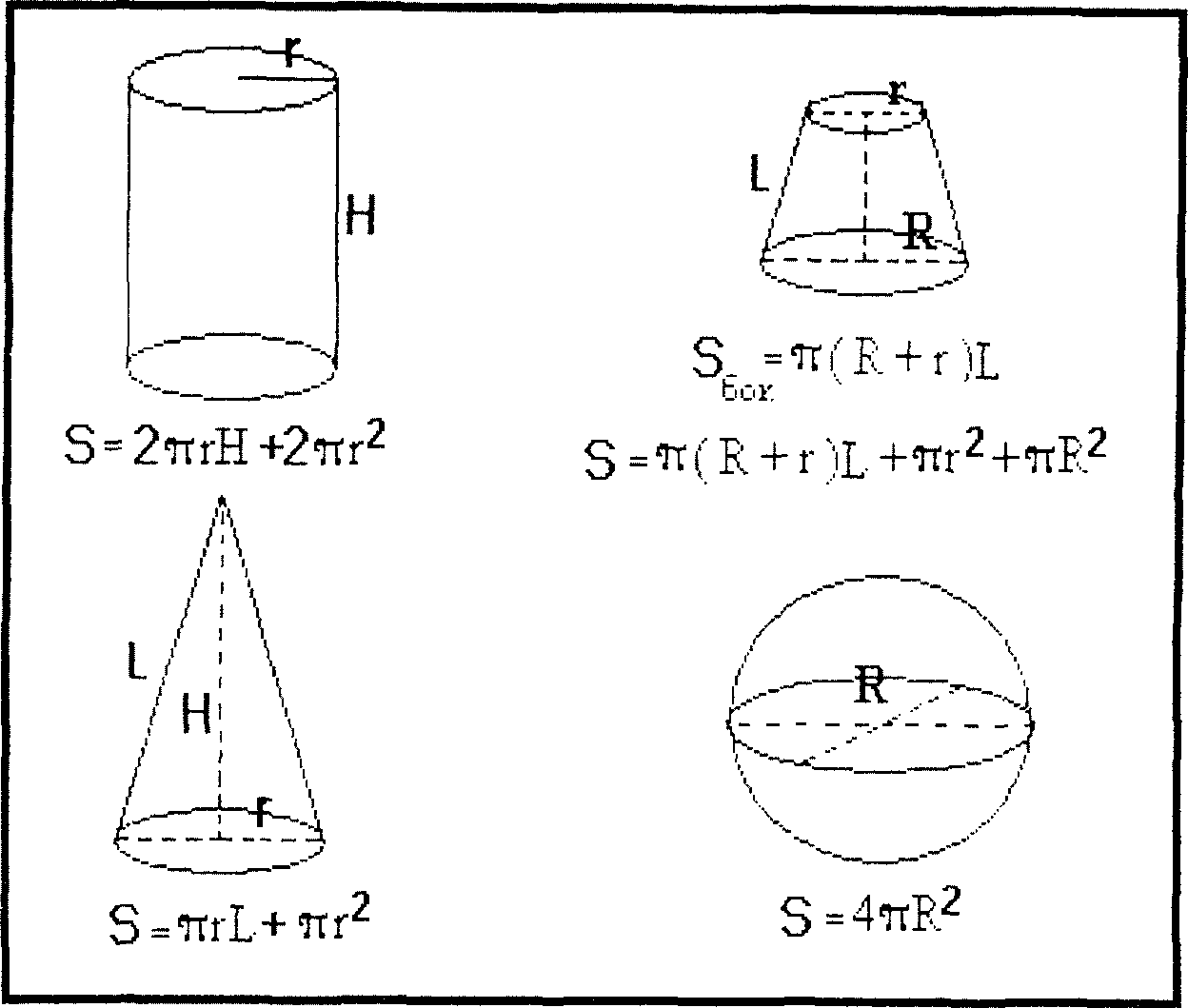
Рис. 1.3. Площади объемных фигур

1.4.

---