Как найти площадь мыльного пузыря

Мыльный пузырь — тонкая многослойная плёнка мыльной воды, наполненная воздухом, обычно в виде сферы с переливчатой поверхностью. Мыльные пузыри обычно существуют лишь несколько секунд и лопаются при прикосновении или самопроизвольно. Их часто используют в своих играх дети.

Из-за недолговечности мыльный пузырь стал синонимом чего-то привлекательного, но бессодержательного и недолговечного. Иногда акции на новых рынках сравнивают с мыльными пузырями, в случае искусственного раздутия их ценности их называют «дутыми».

Структура стенки мыльного пузыря[править | править код]

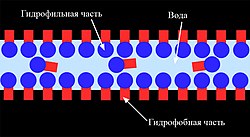
Плёнка пузыря состоит из тонкого слоя воды, заключённого между двумя слоями молекул, чаще всего мыла. Эти слои содержат в себе молекулы, одна часть которых является гидрофильной, а другая гидрофобной. Гидрофильная часть привлекается тонким слоем воды, в то время как гидрофобная, наоборот, выталкивается. В результате образуются слои, защищающие воду от быстрого испарения, а также уменьшающие поверхностное натяжение.

Физические основы[править | править код]

Поверхностное натяжение и форма[править | править код]

Пузырь существует потому, что поверхность любой жидкости (в данном случае воды) имеет некоторое поверхностное натяжение, которое делает поведение поверхности похожим на поведение чего-нибудь эластичного. Однако пузырь, сделанный только из воды, нестабилен и быстро лопается. Для того, чтобы стабилизировать его состояние, в воде растворяют какие-нибудь поверхностно-активные вещества, например мыло. Распространённое заблуждение состоит в том, что мыло увеличивает поверхностное натяжение воды. На самом деле оно делает как раз обратное: уменьшает поверхностное натяжение примерно до трети от поверхностного натяжения чистой воды. Когда мыльная плёнка растягивается, концентрация мыльных молекул на поверхности уменьшается, увеличивая при этом поверхностное натяжение. Таким образом мыло избирательно усиливает слабые участки пузыря, не давая им растягиваться дальше. В дополнение к этому, мыло предохраняет воду от испарения, тем самым делая время жизни пузыря ещё больше.

Сферическая форма пузыря также получается за счёт поверхностного натяжения. Силы натяжения формируют сферу потому, что сфера имеет наименьшую площадь поверхности при данном объёме. Эта форма может быть существенно искажена потоками воздуха и самим процессом надувания пузыря. Однако, если оставить пузырь плавать в спокойном воздухе, его форма очень скоро станет близкой к сферической.

Замерзание пузырей[править | править код]

Имеются свидетельства замерзания мыльных пузырей при температуре около −10 °C^[1]. В целях предотвращения разрушения пузыря при замерзании, рекомендуется надувать мыльный пузырь воздухом уличной температуры (например, быстрым перемещением кольца), а не теплым воздухом изо рта.

Если надуть пузырь при температуре −15 °C, то он замёрзнет при соприкосновении с поверхностью. Воздух, находящийся внутри пузыря, будет постепенно просачиваться наружу и в конце концов пузырь разрушится под действием собственного веса.

При температуре −25 °C пузыри замерзают в воздухе и могут разбиться при ударе о землю. Если при такой температуре надуть пузырь тёплым воздухом, то он замёрзнет почти в идеальной сферической форме, но по мере того, как воздух будет охлаждаться и уменьшаться в объёме, пузырь может частично разрушиться, и его форма будет искажена. Пузыри, надутые при такой температуре, всегда будут небольшими, так как они будут быстро замерзать, и если продолжать их надувать, то они лопнут.

Объединение пузырей[править | править код]

Когда два пузыря соединяются, они принимают форму с наименьшей возможной площадью поверхности. Их общая стенка будет выпячиваться внутрь большего пузыря, так как меньший пузырь имеет бо́льшую среднюю кривизну и большее внутреннее давление. Если пузыри одинакового размера, их общая стенка будет плоской.

Правила, которым подчиняются пузыри при соединении, были экспериментально установлены в XIX веке бельгийским физиком Жозефом Плато и доказаны математически в 1976 г. Жаном Тейлором(Jean Taylor  (англ.) (рус.).

• Мыльные плёнки представляют собой кусочно гладкие поверхности, средняя кривизна которых постоянна на каждом гладком участке.
• Если пузырей больше чем три, они будут располагаться таким образом, что возле одного края могут соединяться только три стенки, при этом углы между ними будут равны 120°, в силу равенства поверхностного натяжения для каждой соприкасающейся поверхности.
• Линии пересечения поверхностей пересекаются в одной точке по четыре штуки, причём угол между любыми двумя равен arccos(-1/3)≈109,47°.

Пузыри, не подчиняющиеся этим правилам, в принципе могут образовываться, однако будут сильно неустойчивыми и быстро примут правильную форму либо разрушатся. Пчёлы, которые стремятся уменьшить расход воска, соединяют соты в ульях также под углом 120°, формируя, тем самым, правильные шестиугольники.

Интерференция и отражения[править | править код]

Переливчатые «радужные» цвета мыльных пузырей наблюдаются вследствие интерференции световых волн и определяются толщиной мыльной плёнки.

Когда луч света проходит сквозь тонкую плёнку пузыря, часть его отражается от внешней поверхности, формируя первый луч, в то время как другая часть проникает внутрь плёнки и отражается от внутренней поверхности, образуя второй луч. Наблюдаемый в отражении цвет излучения определяется интерференцией этих двух лучей. Поскольку каждый проход света через плёнку создаёт сдвиг по фазе пропорциональный толщине плёнки и обратно пропорциональный длине волны, результат интерференции зависит от двух величин. Отражаясь, некоторые волны складываются в фазе, а другие в противофазе, и в результате белый свет, сталкивающийся с плёнкой, отражается с оттенком, зависящим от толщины плёнки.

По мере того, как плёнка становится тоньше из-за испарения воды, можно наблюдать изменение цвета пузыря. Более толстая плёнка убирает из белого света красный компонент, делая тем самым оттенок отражённого света сине-зелёным. Более тонкая плёнка убирает жёлтый (оставляя синий свет), затем зелёный (оставляя пурпурный), и затем синий (оставляя золотисто-жёлтый). В конце концов стенка пузыря становится тоньше, чем длина волны видимого света, все отражающиеся волны видимого света складываются в противофазе и мы перестаем видеть отражение совсем (на тёмном фоне эта часть пузыря выглядит «чёрным пятном»). Когда это происходит, толщина стенки мыльного пузыря меньше 25 нанометров, и пузырь, скорее всего, скоро лопнет.

Эффект интерференции также зависит от угла, с которым луч света сталкивается с плёнкой пузыря. Таким образом, даже если бы толщина стенки была везде одинаковой, мы бы всё равно наблюдали различные цвета из-за движения пузыря. Но толщина пузыря постоянно меняется из-за гравитации, которая стягивает жидкость в нижнюю часть так, что обычно мы можем наблюдать полосы различного цвета, которые движутся сверху вниз.

• 

  В этой диаграмме луч света сталкивается с поверхностью в точке X. Часть света отражается, а часть проходит через внешнюю поверхность и отражается от внутренней.

• 

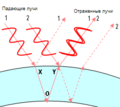
  На этой диаграмме изображены два луча красного света (лучи 1 и 2). Оба луча разбиваются на два, но нас интересуют только те части, которые изображены сплошными линиями. Рассмотрим луч, выходящий из точки Y. Он состоит из двух лучей, наложившихся один на другой: части луча 1, которая прошла через стенку пузыря и части луча 2, которая отразилась от внешней поверхности. Луч, прошедший через точки XOY путешествовал дольше луча 2. Допустим, случилось так, что длина XOY пропорциональна длине волны красного света, поэтому два луча складываются в фазе.

• 

  Эта диаграмма похожа на предыдущую, за исключением того, что длина волны света другая. В этот раз расстояние XOY непропорционально длине волны, и лучи складываются в противофазе. В результате, синий свет не отражается от пузыря с такой толщиной стенки.

• 

  Это компьютерное изображение показывает цвета, отражённые тонкой плёнкой воды, освещённой неполяризованным белым светом.

Математические свойства[править | править код]

Мыльные пузыри также являются физической иллюстрацией проблемы минимальной поверхности, сложной математической задачи. Например, несмотря на то, что с 1884 года известно, что мыльный пузырь имеет минимальную площадь поверхности при заданном объёме, только в 2000 году было доказано^[2], что два объединённых пузыря также имеют минимальную площадь поверхности при заданном объединённом объёме. Эта задача была названа теоремой двойного пузыря. Утверждение о том, что тройной пузырь также имеет минимальную площадь поверхности, было доказано лишь в 2022 году^[3].

С развитием геометрической теории меры удалось доказать, что оптимальная поверхность будет кусочно-гладкой, а не бесконечно изломанной.

Плёнка мыльного пузыря всегда стремится минимизировать свою площадь поверхности. Это связано с тем, что свободная энергия жидкой плёнки пропорциональна площади её поверхности и стремится к достижению минимума:

где  — поверхностное натяжение вещества,

 — полная площадь поверхности плёнки.

Для отдельного пузыря минимальная по площади поверхность — сфера, однако несколько объединённых пузырей имеют гораздо более сложную форму.

Шоу мыльных пузырей[править | править код]

Шоу мыльных пузырей — это и развлечение, и искусство. Создание эффектных пузырей требует от артиста высокого уровня мастерства, а также способности приготовить мыльный раствор идеального качества. Некоторые художники создают гигантские пузыри, часто обертывающие объекты или даже людей. Другим удаётся создать пузыри в форме куба, тетраэдра и других фигур. Часто, для усиления визуального эффекта, пузыри заполняют дымом или горючим газом, сочетают с лазерной иллюминацией или открытым огнём.

Рекорды[править | править код]

2 марта 2017 года россиянка Людмила Дарьина установила рекорд «Книги рекордов Гиннесса» «Наибольшее количество человек внутри мыльного пузыря»^[4] — 374 человека. 30 января 2018 года этот рекорд был внесён и в «Книгу рекордов России»]^[5] как мировой.

Фотография рекорда

История[править | править код]

Плато, Жозеф один из первых в Европе научно изучал фигуры из мыльных пленок, описал результаты и сформулировал проблему, носящую его имя: проблему Плато. В простейшей формулировке её можно сформулировать следующим образом: «найти поверхность наименьшей площади, ограниченную данным замкнутым пространственным контуром». Он же и предложил её физическое решение с помощью мыльных плёнок.

См. также[править | править код]

• Антипузырь
• Законы Плато

Примечания[править | править код]

Литература[править | править код]

• «Charles V. Boys» Soap-Bubbles. Their colors and the forces which mold them. — Dover Publications, New York 1990, ISBN 0-486-20542-8
• «Cyriel Isenberg» The Science of Soap Films and Soap Bubbles. — Tieto Books, Clevedon North Somerset, 1978, ISBN 0-905028-02-3
• Я. Е. Гегузин «Пузыри»
• Flash пособие по изготовлению мыльных пузырей в домашних условиях
• Giant Stinson Beach Bubbles Огромные мыльные пузыри (видео)
• Перельман Я.И. Занимательная физика. Книга 1. Москва: Наука, 1979. 133 с. Глава 5. Свойства жидкостей и газов. Мыльные пузыри// https://www.eduspb.com/public/books/nauch_pop_uch/perelman_fizika1.pdf

Во
многих учебниках по физике описывается
опыт с двумя мыльными пузырями,
соединенными трубкой (рис. 54). В этом
опыте маленький пузырь уменьшается, а
большой – увеличивается. Почему так
происходит? Для объяснения этого выведем
формулу для давления под кривой
поверхностью жидкости.

Стремление
жидкости к сокращению своей поверхности
приводит к тому, что давление под выпуклой
поверхностью жидкости оказывается
больше, а под вогнутой меньше, чем под
плоской (рис. 55).Силы
дополнительного давления р
направлены к центру кривизны поверхности.
Вычислим это
добавочное давление р
для пузырька газа, находящегося в
жидкости (рис. 56). Пусть под действием
давления р
объём пузырька уменьшился на dV,
а поверхность уменьшилась на dS.

^{Объём
шара равен}

^{
dV
= 4R2
dR.}

Площадь
поверхности равна S
= 4R²

dS
= 8R
dR.

Работа
сжатия внешних сил отрицательна и равна

dA
= – p
dV
= – p
4R²
dR.

Другая
формула для работы: dA
= – 
dS
= – 
8R
dR.

Приравняем
уравнения для работ и получим формулу
Лапласа для сферической поверхности:

^{p
4R2
dR
= 
8R
dR
}

В
общем случае формула
Лапласа
имеет вид

,
(86)

где
R₁
и R₂
– радиусы кривизны двух взаимно
перпендикулярных нормальных сечений.
В формуле (86) радиус кривизны R
считают положительным
(рис. 55 б), если центр кривизны находится
внутри жидкости (при несмачивании), и
радиус кривизны считают отрицательным
(рис. 55 в), если центр кривизны лежит над
поверхностью (смачиваемость).

Частные
случаи формулы Лапласа:

1)
для сферыR₁
= R₂
= R
и p
= 2/R;

2)
для плоскости R₁
= R₂
= 
и р
= 0;

3)
для цилиндрической поверхности жидкости
между двумя параллельными пластинками
(рис. 57): R₁
= R,
R₂
= 
и p
= /R;

4)
мыльный пузырь имеет две сферические
поверхности мыльной плёнки, избыточное
давление которых направлено к центру
мыльного пузыря, поэтому p
= 4/R.

Чем
меньше радиус кривизны поверхности
жидкости, тем больше давление. Этим и
объясняется результат опыта, изображённого
на рис. 54. Хотя можно найти и другое
объяснение, если подсчитать площади
поверхностей двух мыльных пузырей в
начале опыта и одного большого пузыря
в конце опыта.

ТРИЗ-задание
32. Мыльные пузыри

Чаще
всего мыльные пузыри используются
только для развлечений. Какие компоненты
делают пузыри «долгоживущими»? Что
такое «антипузырь»? Как ведут себя
мыльные пузыри на морозе? Можно ли
получить твёрдый мыльный пузырь (зимой
на улице или дома в холодильнике)? А
каково техническое применение мыльных
пузырей? Подумайте, где ещё можно
использовать мыльные пузыри?

ТРИЗ-задание
33.
«Пузырьковые»
технологии

Используя
поисковые системы в сети Интернет,
рассмотрите различные технологии
использования пузырьков в технике и
быту: флотáция, барботаж, эрлифт,
везикулярный процесс, пузырьковая
технология струйной печати. Какие
достоинства и недостатки имеют
пеноматериалы: пенобетон, пенометалл,
пеностекло, пенопласт, поролон? Как
делают газированную воду, кукурузные
палочки, пористый шоколад, пузырьковую
плёнку? Что такое пузырьковая панель?
Как работает воздушно-пузырьковая
стиральная машина? Какой закон в ТРИЗ
рекомендует использовать «смесь»
вещества с пустотой?

Соседние файлы в папке папа Жужа

• #
• #
• #