Как найти площадь н угольника через радиус - Сайт, где вы сможете решить свои вопросы

На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.

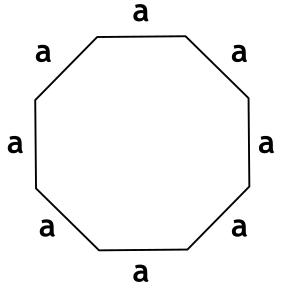
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Содержание:

калькулятор площади правильного многоугольника
формула площади правильного многоугольника через длину стороны
формула площади правильного многоугольника радиус вписанной окружности
формула площади правильного многоугольника радиус описанной окружности
пример задачи

Формула площади правильного многоугольника через длину стороны и число сторон

S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}

a – длина стороны многоугольника

n – число сторон многоугольника

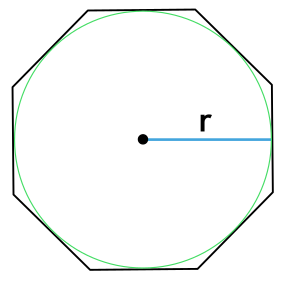
Формула площади правильного многоугольника через радиус вписанной окружности

S = nr^2 tg dfrac{180°}{n}

r – радиус вписанной в многоугольник окружности

n – число сторон многоугольника

Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}

R – радиус описанной в многоугольник окружности

n – число сторон многоугольника

Пример задачи на нахождение площади правильного многоугольника

Задача 1

Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r – радиус вписанной окружности.

Решение

Чтобы решить эту задачу мы используем вторую формулу.

S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2

Ответ: 486 cdot tg 30° approx 280.59223 : см^2

Чтобы проверить ответ воспользуемся калькулятором .

Источник

Найдём площадь правильного многоугольника через радиусы вписанной и описанной окружностей и через его сторону.

Любой правильный многоугольник вписан в окружность и описан около окружности. Центры вписанной и описанной окружностей совпадают и называются центром правильного многоугольника.

Соединив центр правильного n-угольника

$[{A_1}{A_2}{A_3}{A_4}...{A_{n - 1}}{A_n}]$

со всеми его вершинами, получим n равнобедренных треугольников.

Основание каждого такого треугольника равно стороне многоугольника, боковые стороны равны радиусу описанной около многоугольника окружности угол при вершине — центральному углу правильного многоугольника

$[{A_1}{A_2} = a,]$

$[O{A_1} = O{A_2} = R,]$

$[angle {A_1}O{A_2} = frac{{{{360}^o}}}{n}]$

Так как площадь треугольника равна половине произведения его сторон на синус угла между ними,

$[{S_{Delta {A_1}O{A_2}}} = frac{1}{2} cdot {A_1}O cdot {A_2}O cdot sin angle {A_1}O{A_2}.]$

Отсюда

$[{S_{Delta {A_1}O{A_2}}} = frac{1}{2} cdot {R^2} cdot sin frac{{{{360}^o}}}{n}.]$

Поскольку многоугольник состоит из n таких треугольников, формула площади правильного многоугольника через радиус описанной окружности:

$[S = frac{1}{2} cdot {R^2} cdot n cdot sin frac{{{{360}^o}}}{n}.]$

Проведём в треугольнике A1OA2 высоту OF. Её длина равна радиусу вписанной в правильный n-угольник окружности:

По свойству равнобедренного треугольника OF является также его биссектрисой и медианой:

$[angle {A_1}OF = frac{1}{2}angle {A_1}O{A_2} = frac{1}{2} cdot frac{{{{360}^o}}}{n} = frac{{{{180}^o}}}{n},]$

$[{A_1}F = frac{1}{2}{A_1}{A_2}.]$

Из прямоугольного треугольника A1OF по определению тангенса

$[tgangle {A_1}OF = frac{{{A_1}F}}{{OF}},]$

откуда

$[{A_1}F = OF cdot tgangle {A_1}OF = r cdot tgfrac{{{{180}^o}}}{n}.]$

Так как площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне,

$[{S_{Delta {A_1}O{A_2}}} = frac{1}{2} cdot {A_1}{A_2} cdot OF = {A_1}Fcdot OF,]$

$[{S_{Delta {A_1}O{A_2}}} = r cdot tgfrac{{{{180}^o}}}{n} cdot r = {r^2} cdot tgfrac{{{{180}^o}}}{n}.]$

Площадь

$[{A_1}{A_2}{A_3}{A_4}...{A_{n - 1}}{A_n}]$

равна сумме n таких площадей.

Таким образом, формула площади правильного многоугольника через радиус вписанной окружности:

$[S = {r^2} cdot n cdot tgfrac{{{{180}^o}}}{n}.]$

Из треугольника A1OF

$[OF = frac{{{A_1}F}}{{tgangle {A_1}OF}} = frac{{frac{1}{2}{A_1}{A_2}}}{{tgangle {A_1}OF}} = frac{a}{{2tgfrac{{{{180}^o}}}{n}}}.]$

Следовательно,

$[{S_{Delta {A_1}O{A_2}}} = {A_1}F cdot OF = frac{1}{2}a cdot frac{a}{{2tgfrac{{{{180}^o}}}{n}}} = frac{{{a^2}}}{{4tgfrac{{{{180}^o}}}{n}}}.]$

Поскольку многоугольник состоит из n равных треугольников, формула площади правильного многоугольника через его сторону:

$[S = frac{{{a^2} cdot n}}{{4tgfrac{{{{180}^o}}}{n}}}.]$

Источник

Правильный многоугольник

формулы, признаки и свойства правильного многоугольника
формулы правильного n-угольника
правильный треугольник
правильный четырехугольник
правильный шестиугольник
правильный восьмиугольник

Формулы, признаки и свойства правильного многоугольника

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

a1=a2=a3=…=an-1=an

α1=α2=α3=…=αn-1=αn

где a₁…a_n — длины сторон правильного многоугольника,
α₁…α_n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

Все стороны равны:
a1=a2=a3=…=an-1=an
Все углы равны:
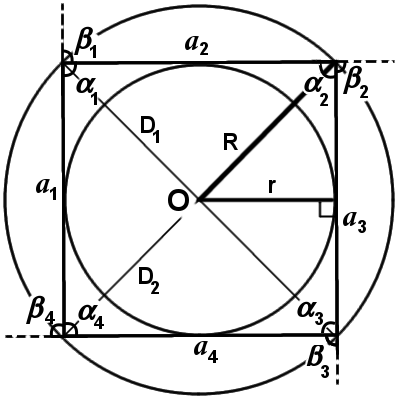
α1=α2=α3=…=αn-1=αn
Центр вписанной окружности O_в совпадает с центром описанной окружности O_о, что и образуют центр многоугольника O.
Сумма всех углов n-угольника равна:180°·n-2
Сумма всех внешних углов n-угольника равна 360°: β1+β2+β3+…+βn-1+βn=360°
Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: Dn = n·n-32
В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π4·a2
Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O.

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности

a = 2·r·tg180°n

(через градусы),

a = 2·r·tgπn

(через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2·R·sin180°n

(через градусы),

a = 2·R·sinπn

(через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

r = a:2·tg180°n

(через градусы),

r = a:2·tgπn

(через радианы)

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a:2·sin180°n

(через градусы),

R = a:2·sinπn

(через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

S = n·a24·ctg180°n

Формула площади n-угольника через радиус вписанной окружности

S = n·r2·tg180°n

Формула площади n-угольника через радиус описанной окружности

S = n·R22·sin360°n

Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

P = n·a

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

αn = n-2n·180°

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

a = 2·r·3

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

a = R·3

r = a·36

R = a·33

Формула площади правильного треугольника через длину стороны

S = a2·34

Формула площади правильного треугольника через радиус вписанной окружности

S = r2·3·3

Формула площади правильного треугольника через радиус описанной окружности

S = R2·3·34

Углы между сторонами правильного треугольника

α1=α2=α3=60°

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

a = 2·r

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

a = R·2

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

r = a2

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

R = a·22

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

S = a2

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

S = 4·r2

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

S = 2·R2

Углы между сторонами правильного четырехугольника

α1=α2=α3=α4=90°

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

a = 2·r·33

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

a = R

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

r = a·32

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

R = a

Формула площади правильного шестиугольника через длину стороны

S = a2·3·32

Формула площади правильного шестиугольника через радиус вписанной окружности

S = r2·2·3

Формула площади правильного шестиугольника через радиус описанной окружности

S = R2·3·32

Углы между сторонами правильного шестиугольника

α1=α2=α3=α4=α5=α6=120°

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

Формулы правильного восьмиугольника

Формула стороны правильного восьмиугольника через радиус вписанной окружности

a = 2·r·2-1

Формула стороны правильного восьмиугольника через радиус описанной окружности

a = R·2-2

Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны

r = a·2+12

Формула радиуса описанной окружности правильного восьмиугольника через длину стороны

R = a·4+222

Формула площади правильного восьмиугольника через длину стороны

S = a2·2·2+1

Формула площади правильного восьмиугольника через радиус вписанной окружности

S = r2·8·2-1

Формула площади правильного восьмиугольника через радиус описанной окружности

S = R2·2·2

Углы между сторонами правильного восьмиугольника

α1=α2=α3=α4=α5=α6=α7=α8=135°

Коротко о важном
Таблицы
Формулы
Формулы по геометрии
Теория по математике

Источник

Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника

Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие:

Все стороны и углы одинаковы:

a₁ = a₂ = a₃ = … = a_n-1 = a_n

α₁ = α₂ = α₃ = … = α_n-1 = α_n

Основные свойства правильного многоугольника

1. Все стороны равны:

a₁ = a₂ = a₃ = … = a_n-1 = a_n

2. Все углы равны:

α₁ = α₂ = α₃ = … = α_n-1 = α_n

3. Центр вписанной окружности O_в совпадает з центром описанной окружности O_о, что и образуют центр многоугольника O

4. Сумма всех углов n-угольника равна:

180° · (n – 2)

5. Сумма всех внешних углов n-угольника равна 360°:

β₁ + β₂ + β₃ + … + β_n-1 + β_n = 360°

6. Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:

7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:

8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O

Правильный n-угольник – формулы

Формулы длины стороны правильного n-угольника

1. Формула стороны правильного n-угольника через радиус вписанной окружности:

2. Формула стороны правильного n-угольника через радиус описанной окружности:

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны:

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны:

Формулы площади правильного n-угольника

1. Формула площади n-угольника через длину стороны:

2. Формула площади n-угольника через радиус вписанной окружности:

3. Формула площади n-угольника через радиус описанной окружности:

Формула периметра правильного многоугольника:

Формула периметра правильного n-угольника:

P = na

Формула определения угла между сторонами правильного многоугольника:

Формула угла между сторонами правильного n-угольника:

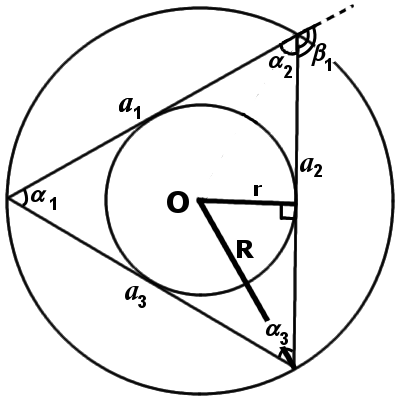Изображение правильного треугольника с обозначениями

Рис.3

Правильный треугольник

Формулы правильного треугольника:

1. Формула стороны правильного треугольника через радиус вписанной окружности:

a = 2r √3

2. Формула стороны правильного треугольника через радиус описанной окружности:

a = R√3

3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:

4. Формула радиуса описанной окружности правильного треугольника через длину стороны:

5. Формула площади правильного треугольника через длину стороны:

6. Формула площади правильного треугольника через радиус вписанной окружности:

S = r² 3√3

7. Формула площади правильного треугольника через радиус описанной окружности:

8. Угол между сторонами правильного треугольника:

α = 60°

Изображение правильного четырехугольнику с обозначениями

Рис.4

Правильный четырехугольник

Правильный четырехугольнику – квадрат.

Формулы правильного четырехугольника:

1. Формула стороны правильного четырехугольника через радиус вписанной окружности:

a = 2r

2. Формула стороны правильного четырехугольника через радиус описанной окружности:

a = R√2

3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:

4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:

5. Формула площади правильного четырехугольника через длину стороны:

S = a²

6. Формула площади правильного четырехугольника через радиус вписанной окружности:

S = 4 r²

7. Формула площади правильного четырехугольника через радиус описанной окружности:

S = 2 R²

8. Угол между сторонами правильного четырехугольника:

α = 90°

Правильный шестиугольник

Формулы правильного шестиугольника:

1. Формула стороны правильного шестиугольника через радиус вписанной окружности:

2. Формула стороны правильного шестиугольника через радиус описанной окружности:

a = R

3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:

4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:

R = a

5. Формула площади правильного шестиугольника через длину стороны:

6. Формула площади правильного шестиугольника через радиус вписанной окружности:

S = r² 2√3

7. Формула площади правильного шестиугольника через радиус описанной окружности:

8. Угол между сторонами правильного шестиугольника:

α = 120°

Правильный восьмиугольник

Формулы правильного восьмиугольника:

1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:

a = 2r · (√2 – 1)

2. Формула стороны правильного восьмиугольника через радиус описанной окружности:

a = R√2 – √2

3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:

4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:

5. Формула площади правильного восьмиугольника через длину стороны:

S = a² 2(√2 + 1)

6. Формула площади правильного восьмиугольника через радиус вписанной окружности:

S = r² 8(√2 – 1)

7. Формула площади правильного восьмиугольника через радиус описанной окружности:

S = R² 2√2

8. Угол между сторонами правильного восьмиугольника:

α = 135°

Источник

Площадь правильного многоугольника по радиусу описанной окружности и количеству сторон

Калькулятор рассчитывает площадь правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон.

Введите радиус описанной окружности R

Введите количество сторон многоугольника n

Формула площади правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон

Где R – радиус описанной около правильного многоугольника окружности,
n – количество сторон правильного многоугольника

Вывод формулы площади правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон

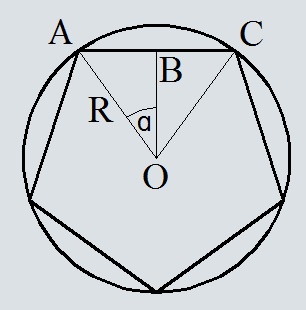
Треугольники AOB и COB равны и являются прямоугольными.

AO=OC=R.

Угол α будет равен 360 градусов/(количество сторон * 2)

Площадь треугольника ACO будет равно произведению половины основания AC=2×AB на высоту BO

Затем умножим площадь треугольника ACO на количество сторон правильного многоугольника и получим площадь правильного многоугольника

Заменим sin(2α)=2sin(α)cos(α) и подставим вместо α ранее выведенную формулу

Похожие калькуляторы

Источник