На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Содержание:
- калькулятор площади правильного многоугольника
- формула площади правильного многоугольника через длину стороны
- формула площади правильного многоугольника радиус вписанной окружности
- формула площади правильного многоугольника радиус описанной окружности
- пример задачи
Формула площади правильного многоугольника через длину стороны и число сторон
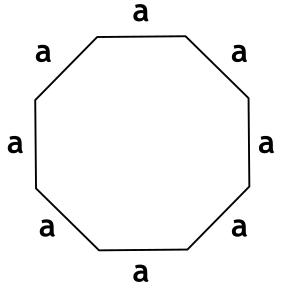
S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}
a – длина стороны многоугольника
n – число сторон многоугольника
Формула площади правильного многоугольника через радиус вписанной окружности
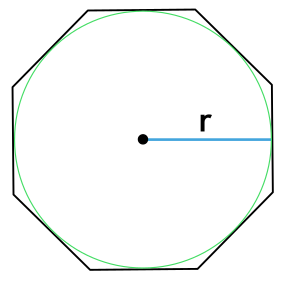
S = nr^2 tg dfrac{180°}{n}
r – радиус вписанной в многоугольник окружности
n – число сторон многоугольника
Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}
R – радиус описанной в многоугольник окружности
n – число сторон многоугольника
Пример задачи на нахождение площади правильного многоугольника
Задача 1
Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r – радиус вписанной окружности.
Решение
Чтобы решить эту задачу мы используем вторую формулу.
S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2
Ответ: 486 cdot tg 30° approx 280.59223 : см^2
Чтобы проверить ответ воспользуемся калькулятором .
Загрузить PDF
Загрузить PDF
Правильный многоугольник представляет собой двумерную выпуклую фигуру, у которой все стороны и углы равны. Площадь некоторых многоугольников, таких как треугольников или четырехугольников, можно найти по простым формулам, но если у многоугольника больше четырех сторон, воспользуйтесь формулой, в которую входит апофема и периметр фигуры.
-

1
Вычислите периметр. Периметр равен сумме всех сторон многоугольника. Если многоугольник правильный, периметр равен произведению одной стороны на число сторон «n».[1]
-

2
Найдите апофему. Апофема — это перпендикуляр, опущенный из центра многоугольника на любую из его сторон. Найти апофему немного сложнее, чем периметр.
- Формула для вычисления апофемы: а = s/(2tg(180/n)), где «s» — сторона, «n» — число сторон.
-

3
Запишите формулу для вычисления площади. Площадь любого правильного многоугольника вычисляется по формуле: S = (a * p)/2, где «a» — апофема, «p» — периметр.
-

4
Подставьте значения «а» и «р» в формулу, чтобы вычислить площадь. Для примера рассмотрим шестиугольник (n = 6), сторона которого равна 10 см (s = 10).
- Периметр: р = n * s = 6 * 10 = 60.
- Вычислите апофему. а = s/(2tg(180/n)) = 10/(2tg(180/6)) = 10/1,1547 = 8,66.
- Площадь многоугольника: S = (a * p)/2 = (8,66 * 60)/2 = 259,8 см2.
- Обратите внимание, что (8,66 * 60)/2 = (8,66/2) * 60 = 8,66 * (60/2), то есть на 2 можно сначала разделить апофему или периметр, а не произведение апофемы и периметра. При этом вы получите один и тот же результат.
Реклама
-

1
Представьте правильный многоугольник как совокупность нескольких треугольников. Каждая сторона многоугольника представляет собой основание треугольника; таким образом, число треугольников равно числу сторон многоугольников. Все треугольники равны, то есть равны их стороны и высоты.[2]
-

2
Вспомните формулу для вычисления площади треугольника. S = 1/2bh, где «b» — основание треугольника (которое совпадает со стороной многоугольника), «h» — высота треугольника (которая совпадает с апофемой правильного многоугольника).[3]
-

3
Обратите внимание на сходство формул. Формула для вычисления площади правильного многоугольника S = 1/2аp, где «а» — сторона многоугольника, «р» — периметр многоугольника. Периметр равен стороне, умноженной на число сторон («n»); в правильном многоугольнике «n» равно числу треугольников, составляющих многоугольник. Таким образом, формула для вычисления площади многоугольника представляет собой формулу для вычисления площади треугольника, умноженную на количество треугольников в многоугольнике.[4]
Реклама
Советы
- Если правильный многоугольник разделен на треугольники, а площадь одного треугольника дана, вычислять апофему не нужно. Просто умножьте площадь одного треугольника на количество сторон многоугольника.
Реклама
Об этой статье
Эту страницу просматривали 27 374 раза.
Была ли эта статья полезной?
Правильным многоугольником считается тот многоугольник, у которого все стороны равны. При соблюдении этого условия, если соединить центр фигуры со всеми углами, то мы увидим столько одинаковых равнобедренных треугольников, сколько сторон в многоугольнике. Основываясь на этом, можно сделать вывод, что площадь правильного многоугольника – это сумма n-ного количества площадей треугольников, а точнее S=nS∆.
Площадь каждого треугольника  , где
, где  .
.
Собираем общую формулу: 
Как рассчитать площадь правильного многоугольника
На данной странице калькулятор поможет рассчитать площадь правильного многоугольника онлайн. Для расчета задайте длину стороны и число сторон.
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.
Через сторону
a:
n:
Результат
Ответы:
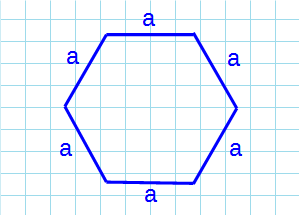
Формула для нахождения площади правильного многоугольника:
a – сторона шестиугольника; n – количество сторон.
Download Article
Download Article
A regular polygon is a 2-dimensional convex figure with congruent sides and angles equal in measure.[1]
Many polygons, such as quadrilaterals or triangles have simple formulas for finding their areas, but if you’re working with a polygon that has more than four sides, then your best bet may be to use a formula that uses the shape’s apothem[2]
and perimeter. With a little bit of effort, you can find the area of regular polygons in just a few minutes.
-

1
Calculate the perimeter. The perimeter is the combined length of the outline of any two-dimensional figure. For a regular polygon, it can be calculated by multiplying the length of one side by the number of sides (n).[3]
-

2
Determine the apothem. The apothem of a regular polygon is the shortest distance from the center point to one of the sides, creating a right angle. This is a little trickier to calculate than the perimeter.[4]
- The formula for calculating the length of the apothem is this: the length of the side (s) divided by 2 times the tangent (tan) of 180 degrees divided by the number of sides (n).
Advertisement
-

3
Know the correct formula. The area of any regular polygon is given by the formula: Area = (a x p)/2, where a is the length of the apothem and p is the perimeter of the polygon.
-

4
Plug the values of a and p in the formula and get the area. As an example, let’s use a hexagon (6 sides) with a side (s) length of 10.[5]
- The perimeter is 6 x 10 (n x s), equal to 60 (so p = 60).
- The apothem is calculated by its own formula, by plugging in 6 and 10 for n and s. The result of 2tan(180/6) is 1.1547, and then 10 divided by 1.1547 is equal to 8.66.
- The area of the polygon is Area = a x p / 2, or 8.66 multiplied by 60 divided by 2. The solution is an area of 259.8 units.
- Note as well, there are no parenthesis in the “Area” equation, so 8.66 divided by 2 multiplied by 60, will give you the same result, just as 60 divided by 2 multiplied by 8.66 will give you the same result.
Advertisement
-

1
Understand that a regular polygon can be thought of as a collection of triangles. Each side represents the base of a triangle, and there are as many triangles in the polygon as there are sides. Each of the triangles are equal in base length, height, and area.[6]
-

2
Remember the formula for the area of a triangle. The area of any triangle is 1/2 times the length of the base (which, in the polygon, is the length of a side) multiplied by the height (which is the same as the apothem in regular polygon).[7]
-

3
See the similarities. Again, the formula for a regular polygon is 1/2 times the apothem multiplied by the perimeter. The perimeter is just the length of one side multiplied the by the number of sides (n); for a regular polygon, n also represents the number of triangles that make up the figure. The formula, then, is nothing more than the area of a triangle multiplied by the number of triangles in the polygon.[8]
Advertisement
Add New Question
-
Question
How do I find the perimeter of a regular polygon with one side being 5-2x and another being -4x+9?

Since a regular polygon has congruent sides (every side is equal to each other) you set up the equation 5-2x = -4x+9 then you solve for “x”. After solving for “x”, you substitute the answer you got from “x” back into the one of the expressions from one of the sides. You should get the answer of how many units one of the sides is. After that, just multiply that answer by how many sides the polygon has to get your perimeter.
-
Question
How do I find the perimeter of a nonagon with area of 28.8 and side length of 21?

The perimeter equals the side length times the number of sides. In this case, multiply 21 by 9 and you will get a perimeter of 189.
-
Question
What is the area of a polygon with sides of 12m, 11m, 3m, and 3m?

Since the given measurements of the sides best represents a trapezoid, you use the area of a trapezoid equation A=h*((b1+b2)*0.5) where A is the area, h is the height of the trapezoid, and where b1 is the top base and b2 is the bottom base. To find the height, you subtract b2 by b1, then divide it, then substitute that answer into “a” of the Pythagorean theorem a^2+b^2=c^2, where “c” equals the length of the side of your trapezoid which in this case is 3m. You solve for b in that equation to get your height. Once you got the measurement of the height of the trapezoid, you use the area of a trapezoid equation and substitute your answers in it to get your area.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If the drawing of your polygon has been separated into triangles, and one triangle’s area is labeled, then you do not need to know the apothem. Just take the area of that one triangle, and multiply by the number of sides in the original polygon.
Advertisement
Area Help
References
About This Article
Article SummaryX
To find the area of regular polygons, use the formula: area = (ap)/2, where a is the apothem and p is the perimeter. To find the apothem, divide the length of one side by 2 times the tangent of 180 degrees divided by the number of sides. To find the perimeter, multiply the length of one side by the total number of sides. Once you’ve found the apothem and the perimeter, plug them into the formula for area and solve. If you want to learn more about how finding the apothem works for calculating the area, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 805,140 times.
Reader Success Stories
-

“Thank you, this really helped me understand how the formula was actually created for my geometry test because I…” more
