Одним из многогранников, которые изучают в школах в курсе пространственной геометрии, является пирамида. Эта фигура имеет ряд параметров и характеристик, для вычисления которых используют определенные математические формулы. Прочитав статью, вы узнаете, как находить площадь поверхности пирамиды.
Что представляет собой пирамида? Виды фигуры
Речь идет о фигуре в трехмерном пространстве, которая представляет собой многогранник, состоящий из треугольников и многоугольника. Если взять произвольный многоугольник на плоскости и соединить все его вершины прямыми отрезками с какой-нибудь точкой, не принадлежащей плоскости этого многоугольника, то мы получим пирамиду произвольного типа.
Пирамида состоит из граней, вершин и ребер. Грани представляют собой плоскости, ограничивающие объем фигуры. Грани разделены друг от друга ребрами. Если три грани пересекаются в одной точке, то последняя является вершиной. Любая такая фигура имеет несколько вершин, например, у треугольной фигуры их четыре, а у четырехугольной – пять. У каждой пирамиды есть только одна вершина, которая не принадлежит основанию. Она называется главной или основной.
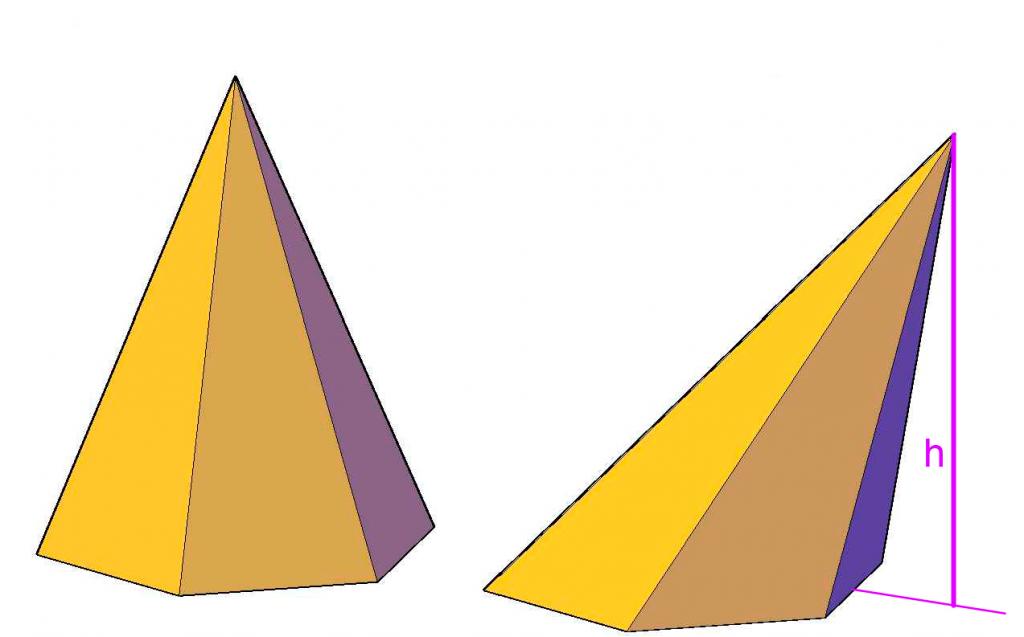
Класс пирамид включает несколько типов фигур. Пирамида будет прямой, если ее боковые треугольники являются равнобедренными. Если эти треугольники еще и равны друг другу, тогда фигура будет правильной. У любой прямой и правильной пирамиды высота (расстояние от главной вершины до основания) пересекает основание в его геометрическом центре. Кроме того, правильная фигура обладает равносторонним (равноугольным) основанием.
Площадь поверхности пирамиды
Под площадью любой подобной фигуры понимают сумму площадей всех ее сторон. Поскольку пирамиды имеют разный тип, то для расчета их площадей не существует универсальной формулы. Однако существуют выражения, которые могут быть использованы в каждом конкретном случае.
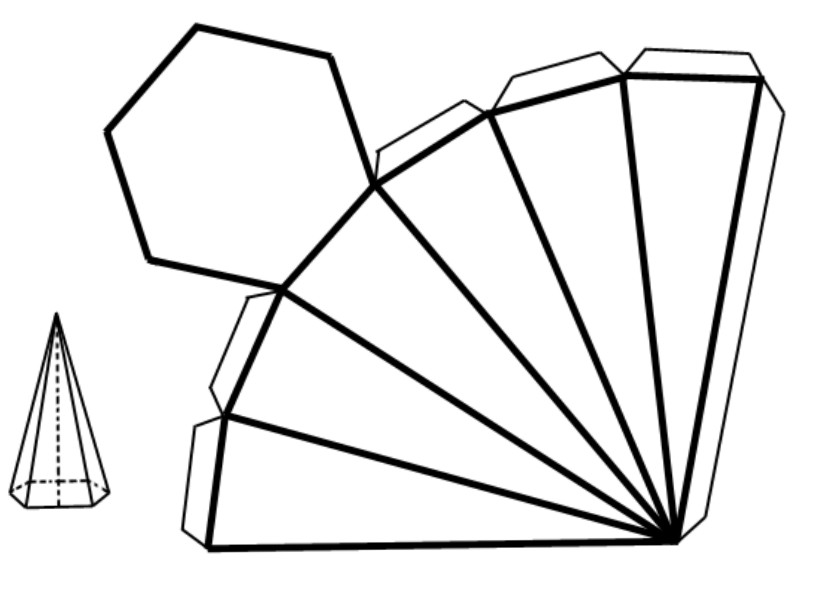
Какой бы не была пирамида, она всегда состоит из n-угольной грани и n треугольников. Площадь треугольников вычислить несложно, если известны их высоты и стороны основания. Что касается n-угольника, то для определения его площади следует провести анализ, что это за n-угольник, является ли он правильным, какие его углы известны. Универсальным методом определения его площади является разбиение на более простые фигуры, например, треугольники или параллелограммы.

Правильная фигура
Для правильной пирамиды формула площади поверхности давно уже определена. Прежде чем ее записывать, отметим, что площадь правильного основания фигуры может быть вычислена так:
Sn = n/4*a2*ctg(pi/n).
В формуле: a – сторона многоугольника, n – число сторон в нем. Например, для треугольника формула выглядит следующим образом:
S3 = √3/4*a2.
Для квадрата же получаем типичное равенство:
S4 = a2
Для правильной пирамиды площадь поверхности боковой Sb может быть определена по такой формуле:
Sb = n/2*hb*a.
Где hb – апофема пирамиды (высота бокового треугольника).
Складывая выражения для Sn и Sb, получаем формулу площади полной поверхности пирамиды:
S = Sn + Sb = n/4*a2*ctg(pi/n) + n/2*hb*a.
Отметим, для однозначного определения S любой пирамиды правильной необходимо знать два ее линейных параметра.
Наклонная фигура
Площадь поверхности пирамиды наклонной рассчитать гораздо сложнее, чем правильной. Тем не менее, зная ее развертку, всегда можно решить поставленную задачу. Боковая поверхность наклонной фигуры рассчитывается так:
Sb = 1/2*∑i=1n(ai*hbi).
Здесь ai – длина i-й стороны основания, hbi – длина i-й апофемы. Апофемы для наклонной пирамиды общего типа различаются.
Площадь основания So вычисляется, исходя из его типа, например, если это параллелограмм со сторонами a1 и a2 и углом между ними θ, тогда можно записать:
So = a1*a2*sin(θ).
Как для наклонной, так и для прямой пирамиды апофемы связаны с длинами боковых ребер и ребер основания. Эту связь часто используют при решении задач.
Как рассчитать площадь поверхности AutoCAD 3d?
- Выберите вкладку «Главная» панель «Утилиты» раскрывающийся список «Измерить площадь». Находить.
- В командной строке введите o (Объект).
- Выберите объект.
Как определить размер 3D-объекта в AutoCAD?
Разместите размер с помощью ПСК:
- Перейдите на вкладку «Главная».
- Наведите указатель мыши на панель координат.
- Нажмите на исходную UCS.
- Поместите ПСК на грань объекта, где необходимо добавить размер.
- Перейдите на вкладку «Аннотации».
- Щелкните Размер.
- Поместите размер там, где это необходимо.
Как найти площадь наклонной поверхности?
Умножить гипотенузу на длину крыши. Результатом является площадь поверхности наклонной крыши. Например, если наклонная поверхность имеет ширину 11.18 фута, а длина крыши 30 футов, площадь наклона составляет 335.4 квадратных фута — 11.18 х 30 = 335.4.
Что такое формула площади?
Для прямоугольника длиной l и шириной w формула для вычисления площади имеет следующий вид: A = lw (прямоугольник). То есть площадь прямоугольника – это длина, умноженная на ширину. В качестве особого случая, поскольку l = w в случае квадрата, площадь квадрата со стороной s определяется по формуле: A = s2 (площадь).
Как измерить площадь?
Основная формула квадратных футов
Умножьте длину на ширину, и вы получите квадратные футы. Вот основная формула, которой вы можете следовать: Длина (в футах) x ширина (в футах) = площадь в кв.
По какой формуле можно найти площадь и объем трехмерных фигур любых 3-х фигур)?
Блок 9 Раздел 4: Площадь поверхности и объем трехмерных фигур
| Cubo,en | Объем = x³ Площадь = 6x² |
|---|---|
| Кубоид | Объем = xyz Площадь поверхности = 2xy + 2xz + 2yz |
| цилиндр | Объем = π r²h Площадь криволинейной поверхности = 2π rh Площадь каждого конца = π r² Общая площадь поверхности = 2π rh + 2π r² |
Как найти площадь поверхности неправильной трехмерной фигуры?
Для обычной призмы (у которой все стороны одинаковые) вычислите площадь одной из сторон и умножьте на общее количество сторон. Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны. Сложите два ответа вместе (концы × стороны) чтобы найти общую площадь призмы.
Что такое три измерения?
Трехмерная вселенная состоит из трех измерений, ширина, ширина и высота.
Вычислить площадь квадрата так же просто, как умножить длину на ширину. Но когда у вас есть изогнутая поверхность, такая как сфера или цилиндр, проблема может быть загадочной. К счастью, математики разработали формулы для криволинейных поверхностей, поэтому все, что вам нужно сделать, – это выполнить пару простых измерений и включить измерения в формулы. Например, если вы знаете радиус сферы, вы можете использовать формулу 4 pi r ^ 2 для расчета площади ее поверхности. Площадь поверхности цилиндра может быть рассчитана по высоте и радиусу по формуле 2 pi r ^ 2 + 2 pi r h.
Площадь поверхности сферы
Квадратный радиус. Например, если радиус составляет 5 дюймов, то: 5 дюймов * 5 дюймов = 25 дюймов в квадрате.
Умножьте Шаг 1 на Пи. Pi * 25 дюймов в квадрате = 78, 54 дюйма в квадрате.
Умножьте Шаг 2 на 4: 78, 54 дюйма в квадрате * 4 = 314, 16 дюйма в квадрате.
цилиндр
-
Хотя 3.14 является хорошим приближением к пи и будет работать для большинства вычислений, вы можете повысить точность своих ответов, добавив больше десятичных знаков к пи. Например, используйте 3, 1416 для числа Пи (4 десятичных знака) и 6, 2832 для значения 2pi.
Квадратный радиус. Например, если радиус составляет 2 дюйма, то: 2 дюйма * 2 дюйма = 4 дюйма в квадрате.
Умножьте Шаг 1 на 6, 28. 6, 28 * 4 дюйма = 25, 04 дюйма
Умножьте радиус на высоту. Например, радиус 2 дюйма и высота 10 дюймов дадут вам: 2 дюйма * 10 дюймов = 20 дюймов в квадрате.
Умножьте Шаг 3 на 6, 28: 20 дюймов в квадрате * 6, 28 = 125, 6 дюйма в квадрате.
Добавьте Шаг 2 и Шаг 4 вместе: 25, 04 дюйма в квадрате + 125, 6 дюйма в квадрате = 150, 64 дюйма.
подсказки
Продолжаем повторять формулы стереометрии, на этот раз площадь поверхности. Площадь поверхности любой пространственной фигуры — это сумма всех площадей её граней. Если простыми словами – это площадь той поверхности, которую можно потрогать у фигуры.
✅ Начнём с куба — у него шесть граней, все они квадраты, поэтому площадь каждой равна a^2, а площадь поверхности куба равна 6 • a^2. У прямоугольного параллелепипеда примерно та же история, у него 6 граней, только на этот раз грани — 3 пары прямоугольников. Поэтому формула площади поверхности будет состоять из суммы трёх пар площадей прямоугольников: Sпр = 2 • (ab + bc + ac).
💁🏻♂ Площадь полной поверхности призмы состоит из суммы боковой поверхности и двух площадей основания. С основаниями все более менее понятно, а вот площадь боковой поверхности можно вычислить аж по двум формулам. Первая из них для прямой призмы, а вторая для наклонной призмы.
📌 У прямой призмы все грани — прямоугольники с одинаковой стороной в виде высоты. А вторая сторона каждого прямоугольника — сторона основания многоугольника в основании. Поэтому площадь боковой поверхности прямой призмы можно вычислить как произведение периметра основания на высоту.
📌 У наклонной призмы все грани — параллелограммы, поэтому базовый способ для нахождения площади поверхности — считать каждую грань по отдельности и суммировать все грани. Но это не сильно действенный способ потому, что долго и дорого так делать на экзамене, в задачах чаще всего работает другая формула.
✅ Площадь боковой поверхности наклонной призмы равна произведению бокового ребра на периметр перпендикулярного сечения этому ребру. То есть по сути это та же формула, что и для прямой призмы, только вместо периметра основания используем периметр перпендикулярного сечения, а вместо высоты используем ребро.
👉🏻 Последняя из действенных формул — площадь боковой поверхности правильной пирамиды. Площадь полной поверхности равна сумме площадей боковой поверхности и основания. Все грани правильной пирамиды – равные треугольники, у которых одинаковая высота в виде апофемы боковой грани, и равные стороны основания.
🌟 Поэтому площадь боковой поверхности равна произведению полупериметра на апофему. Одна вторая здесь возникает из-за того, что это коэффициент в каждой площади треугольника грани.
На ЕГЭ нет подсказок в виде формул, поэтому сохраняй картинку, запоминай формулы и применяй их к задачам💕

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
1. Формула площади равнобедренной трапеции через стороны и угол

b – верхнее основание
a – нижнее основание
c – равные боковые стороны
α – угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):



2. Формула площади равнобокой трапеции через радиус вписанной окружности

R – радиус вписанной окружности
D – диаметр вписанной окружности
O – центр вписанной окружности
H – высота трапеции
α, β – углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции
α, β – углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m – средняя линия трапеции
c – боковая сторона
α, β – углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b – верхнее основание
a – нижнее основание
h – высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):

