С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».
Как найти площадь неправильного четырехугольника?
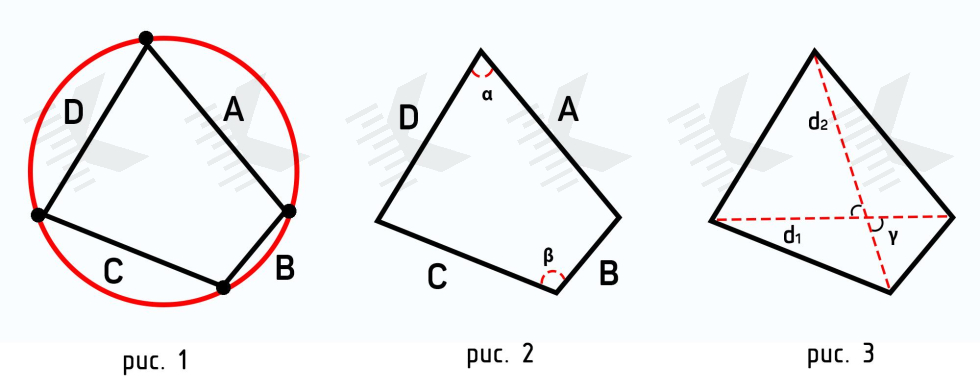
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.
![]()
где P — полупериметр, a, b, c, d — длины сторон четырехугольника.
Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.
![]()
где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.
В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.
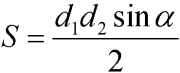
где d1, d2 — диагонали четырехугольника, α — острый угол между диагоналями.
Как вычислить площадь фигуры неправильной формы?
МатематикаГеометрияПлощадь
Анонимный вопрос
22 января 2019 · 103,4 K
Люблю математику, люблю решать задачи и учиться. · 22 янв 2021
Помещаем исходную фигуру F внутри фигуры K1, площадь которой легко посчитать ( например состоящей из квадратов). Далее размещаем внутри F фигуру L1, площадь которой аналогично легко посчитать. Положим
S1=( K1+L1)/2. Если точность оценки – например K1-L1< a – нас устраивает, то S1-искомая площадь. Если не устраивает, на втором шаге помещаем F внутри K2, так чтобы K2 лежала внутри K1, и площадь K2 легко считалась, ( например, заполняем пустоты квадратами меньшего размера.) те сужаем внешний объём и теперь аналогично увеличиваем внутренний: внутри F размещаем L2, содержащую L1. Положим S2=(K2+L2)/2.
Очевидно, что S2>S1 и K2-L2<K1-L1., те точность увеличилась. И тд, пока нас не устроит точность оценки.
18,8 K
Комментировать ответ…Комментировать…
Можно ее начертить в программе Компас 3 D и воспользоваться функцией расчет площади плоской фигуры. Либо разбить на фигуры правильной формы вашу деталь и посчитать методом суммирования и вычитания площадей. Читать далее
13,5 K
Комментировать ответ…Комментировать…
Ученик 4 класса, отличник. Если смогу, обязательно отвечу! · 15 авг 2020
Площадь фигуры неправильной формы можно вычислить так: сначала делим фигуру на квадраты одинаковой формы, потом считаем количество полных квадратов(d) , потом не полных(f) , делим неполные пополам и складывает полные и неполные (разделённые пополам) . Формула: S = d + f : 2
18,3 K
Комментировать ответ…Комментировать…
Проложить по краяю измеряемой фигуры верёвочку, затем измерить длину этой верёвки и сделать из неё правильную геометрическую фигуру (квадрат) и тогда измерять площадь квадрата. Зная высоту неправильной фигуры можно вычислить объём этой фигуры
2,7 K
Если следовать предложенному алгоритму, то конечно будет допущена ошибка. В качестве примера возьмите круг и… Читать дальше
Комментировать ответ…Комментировать…
Инженер
Финансист
Бухгалтер
Начинающий предприниматель
IT · 1 апр 2022
Надо загуглить макросы для Corel Draw. Среди них есть готовые решения. Одна из таких Curve info, там же есть описание как устанавливать. Заодно посмотреть какие версии поддерживаются
1,9 K
Комментировать ответ…Комментировать…
Могу лишь намекнуть принцип. Из физики 8-го класса известно,что ЭДС
фотоэлемента зависит от светового потока ,падающего на него Тогда идея измерения пощади будет заключаться в измерении напряжения ,вырабатываемого фотоэлементом при помощи откалиброванного в еденицах площади измерительного прибора,на который падает поток света. Если подложка из фотоэлемента ,например… Читать далее
13,2 K
Комментировать ответ…Комментировать…
Площадь неправильной фигуры высчитывается таким образом: фигура делится на квадраты, треугольники и прямоугольники так, чтобы они все максимально помещались в эту неправильную фигуру. Вычисляется площадь каждой составляющей фигуры и суммируется. Так, приблизительно подсчитывается площадь неправильной геометрической фигуры.
51,7 K
если не сложно, можно формулой?
(не я вопрос писал)
Комментировать ответ…Комментировать…
When you first start calculating area, you get easy shapes that have clearly defined formulas for finding their area: circles, triangles, squares and rectangles, for example. But what happens when you’re faced with a shape that doesn’t fit easily into those categories? Until you enter the brave new world of calculus integrals, the best way to find the area of irregular shapes is by subdividing them into shapes you’re already familiar with.
TL;DR (Too Long; Didn’t Read)
The simplest way to calculate the area of an irregular shape is to subdivide it into familiar shapes, calculate the area of the familiar shapes, then total those area calculations to get the area of the irregular shape they make up.
-
Note how you carry the units of measure – in this case, inches – throughout the calculations. Always write down your units of measure. Failing to do so is one of the most common errors but also one of the easiest to avoid.
-
Instead of subdividing the irregular shape into something familiar, can you add a piece to make it something familiar? For example, imagine that your shape looks like a square but with one corner cut off at an angle. Can you “add” a triangle to that cut-off corner to make it back into a tidy square? If yes, you can calculate the area of the entire square, then subtract the area of the triangle you just added in. The result will be the area of the irregular shape you started with.
Collect the area formulas for shapes you’re already familiar with. The most common shapes and their formulas include:
text{Area of a square or rectangle } = l × w
where l is length and w is width.
text{Area of a triangle } = frac{1}{2}(b × h)
where b is the triangle’s base and h is its vertical height.
text{Area of a parallelogram } = b × h
where b is the parallelogram’s base and h is its vertical height.
text{Area of a circle } = πr^2
where r is the radius of the circle.
Use your imagination to subdivide the irregular shape you have into more familiar shapes. Sometimes drawing the shape out, then adding lines for the subdivisions, helps you visualize it, and track the appropriate measurements for each dimension. For example, imagine that you have to find the area of a five-sided shape that isn’t a hexagon but has three perpendicular sides opposite the “point.” With a little thinking, you can subdivide this into a rectangle that butts up against a triangle, with the triangle forming the “point” of the shape.
Refer back to your area formulas for the dimensions you’ll need to calculate the area of each subdivided shape. In this case, you’ll need the base and vertical height of the triangle and the length and width (or two adjacent sides) of the rectangle. If you’re working a math problem in school, you’ll probably get at least some of these measurements and may need to use some basic algebra or geometry to find any missing measurements. If you’re working in the real world, you might be able to fill in some of the dimensions by physically measuring.
Fill the dimensions into the area formula for each subdivided shape. For example, if the triangle has a base of 6 inches and a vertical height of 3 inches, its area formula is:
frac{1}{2}(b × h) = frac{1}{2} (6 text{ in} × 3 text{ in}) = frac{1}{2} (18 text{ in}^2) = 9 text{ in}^2
If the rectangle has a length of 6 inches (which is also the side that makes up the base of the triangle) and a height of 4 inches, its area formula is:
l × w = 6 text{ in} × 4 text{ in} = 24 text{ in}^2
Tips
Add the areas of the subdivided shapes; the total is the area of the irregular shape you started with. To conclude this example, the area of the triangle is 9 in2, and the area of the rectangle is 24 in2. So your total area is:
9 text{ in}^2 + 24 text{ in}^2 = 33 text{ in}^2
Tips
Как рассчитать площадь комнаты?
Простая комната прямоугольной или квадратной формы В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах. Формула по которой можно высчитать площадь: S комнаты = А х B, где A – длина, B – ширина.
Видео
Площадь поверхности правильной шестиугольной пирамиды

Пусть сторона основания равна ( displaystyle a), а боковое ребро ( displaystyle b).
( displaystyle {{S}_{полн. пов. }}=4{{text{S}}_{ASB}}+{{text{S}}_{text{осн}.}})Как найти ( displaystyle {{S}_{OCH}})?
Шестиугольник ( displaystyle ABCDEF) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете площади поверхности правильной треугольной пирамиды, здесь используем найденную формулу.
( displaystyle {{S}_{ABCDEF}}=6cdot {{S}_{AOF}}=6cdot frac{{{a}^{2}}sqrt{3}}{4}=frac{3sqrt{3}{{a}^{2}}}{2})Ну, и площадь боковой грани мы уже искали аж два раза
Формула Пика
Существует довольно удобная формула, которая использует клеточки для вычисления площади. А то, что мы только что проделали, – очень полезное упражнение, которое поможет эту формулу понять.
Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.

Теперь вместо клеточек или их частей подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
Сколько насчитали?
У меня получилось ( Г = 22) на границе и ( В = 32) внутри.
Ну а теперь сама формула:
Делим границу пополам, прибавляем внутренности и вычитаем 1:
( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.)
Называется она формулой Пика, поскольку доказал её математик Георг Пик 120 лет назад (да, она не специально для ЕГЭ была придумана, но очень нам помогает) 🙂
Площадь прямоугольника
Запомните! 
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
 SABCD = AB · BC SABCD = 3 · 7 = 21 см2 Запомните!
SABCD = AB · BC SABCD = 3 · 7 = 21 см2 Запомните! 
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны и две не параллельны.
S = 0,5 × (a + b) × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны под прямым углом.
Круг
Круг — это множество точек на плоскости, ограниченных окружностью, удаленных от центра на равном радиусу расстоянии. Радиусом принято называть отрезок, соединяющий центр с любой точкой окружности.
-
S = π × r2, где r — это радиус, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

-
S = &pi × d2 : 4;, где d — это диаметр.

-
S = L2 : (4 × π), где L — это длина окружности.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Навигация по записям
Предыдущая статьяЕсли диагонали то этот параллелограмм является прямоугольником – Признаки прямоугольника и квадрата — урок. Геометрия, 8 класс.
Следующая статья Площадь прямоугольника равняется произведению половины квадрата – Площадь прямоугольника равняется произведению половины квадрата
Теги
как найти площадь неравной фигуры.
Павел Потапов
Ученик
(101),
закрыт
7 лет назад
Mr. President
Мудрец
(14714)
7 лет назад
Нужно разбить неровную фигуру на стандартные фигуры (треугольники, квадраты, прямоугольники и т. д.), вычислить площадь каждой такой фигуры, а потом сложить. Общая сумма площадей и есть площадь неровной фигуры.
