Как найти площадь не стандартного прямоугольника

Давайте вспомним, как найти площадь прямоугольника. Чтобы найти
площадь прямоугольника, надо длину умножить на ширину.

Вот формула для нахождения площади прямоугольника:

S = a · b

В этой формуле латинской буквой S обозначается площадь, буквами a и b  – стороны прямоугольника.

Выполним задание, в котором надо найти площадь
прямоугольника со сторонами 5 см и 3 см.

Решение. Итак, чтобы найти площадь
прямоугольника, надо его длину умножить на ширину.

Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника
равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в
квадратных единицах. В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.

3 · 5 =
15 (см²)

Ответ: площадь прямоугольника равна 15 см².

Теперь давайте найдём площадь квадрата со стороной 4 см.

Решение. У этого квадрата каждая
сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата
равна 16 квадратным сантиметрам.

4 · 4 =
16 (см²)

Ответ: площадь квадрата равна 16 см².

Ну а сейчас перейдём к решению задач, в которых нам надо будет
найти площадь сложных фигур.

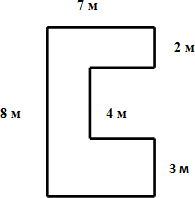
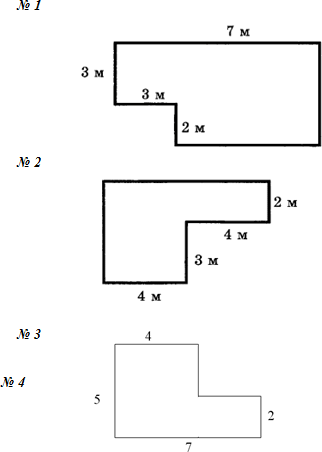
Найдите площадь фигуры, изображённой на рисунке.

Эта фигура не является ни прямоугольником, ни квадратом. Но мы
можем разделить эту фигуру на два прямоугольника, например, вот таким образом.

 А площади прямоугольников мы легко можем найти с помощью
известной формулы.

Напомним, что противоположные стороны прямоугольника равны.

Итак, стороны первого прямоугольника равны 5 см и 4 см.

5 · 4 =
20 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

Ширина этого прямоугольника равна 2 см.

7 – 4 = 3 (см) – длина второго прямоугольника

3 · 2 = 6
(см²) – площадь второго прямоугольника

Мы нашли площади прямоугольников, из которых состоит сложная
фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.

20 + 6 = 26
(см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Площадь этой сложной фигуры найти другим способом. Можно разделить
её на два прямоугольника вот таким образом.

Найдём площадь первого прямоугольника.

Одна его сторона равна 4 см.

5 – 2 = 3 (см) – длина стороны первого прямоугольника

4 · 3 =
12 (см²) – площадь первого прямоугольника

Теперь найдём площадь второго прямоугольника.

7 · 2 =
14 (см²) – площадь второго прямоугольника

12 + 14 =
26 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Решим следующую задачу.

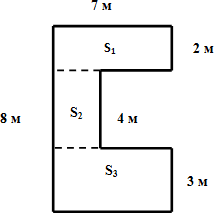
Найдём площадь ещё одной фигуры, изображённой на рисунке.

Чтобы найти площадь этой фигуры, тоже разделим её на простые
фигуры. Сделаем это вот таким образом.

Получилось 3 прямоугольника.

Найдём площадь первого прямоугольника.

7 · 2 =
14 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

7 – 4 = 3 (см) – длина одной стороны второго прямоугольника

8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника

Получается, что это квадрат, так как длина всех его сторон равна 3
см.

3 · 3 = 9
(см²) – площадь квадрата

И найдём площадь последнего прямоугольника.

Его ширина равна 3 см. Длина равна 7 см.

3 · 7 =
21 (см²) – площадь третьего прямоугольника

Таким образом, мы нашли площади всех трёх фигур, на которые
разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму
площадей трёх фигур.

14 + 9 + 21 =
44 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 44 см²

Отметим, что площадь этой фигуры можно было бы найти, разделив её
на простые фигуры и вот таким образом:

И решим ещё одну задачу.

Найдите площадь незаштрихованной фигуры.

На рисунке изображён прямоугольник со сторонами 9 см и 5 см.
Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см
и 3 см. Давайте найдём площадь каждого из них.

9 · 5 =
45 (см²) – площадь большего прямоугольника

5 · 3 =
15 (см²) – площадь меньшего прямоугольника

А как найти площадь незаштрихованной фигуры? Площадь этой фигуры
найдём, если из площади большего прямоугольника вычтем площадь меньшего
прямоугольника.

45 – 15 =
30 (см²) – площадь незаштрихованной фигуры

Ответ: площадь незаштрихованной фигуры равна 30 см².

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S
_ABC = S_ABCD : 2

S
_ABC = 20 : 2 = 10 см²

S
_ABC =
S
_ACD = 10 см²

---

Ваши комментарии

Оставить комментарий:

---

На мой взгляд, задача учителя – не только научить, а развить познавательный интерес у учащегося. Поэтому, когда возможно, связываю темы урока с практическими задачами.

На занятии учащиеся под руководством учителя составляют план решения задач на нахождение площади «сложной фигуры» (для расчеты сметы ремонта), закрепляют навыки решения задач на нахождение площади; происходит развитие внимания, способности к исследовательской деятельности, воспитание активности, самостоятельности.

Работа в парах создает ситуацию общения между теми, кто имеет знания и теми, кто их приобретает; в основе такой работы лежит повышение качества подготовки по предмету. Способствует развитию интереса к процессу учения и более глубокому усвоению учебного материала.

Урок не только систематизирует знания обучающихся, но и способствует развитию творческих, аналитических способностей. Применение задач с практическим содержанием на уроке позволяет показать востребованность математических знаний в повседневной жизни.

Цели урока:

Образовательные:

• закрепление знаний формул площади прямоугольника, прямоугольного треугольника;
• анализ заданий на вычисление площади “сложной” фигуры и способов их выполнения;
• самостоятельное выполнение заданий для проверки знаний, умений, навыков.

Развивающие:

• развитие приёмов умственной и исследовательской деятельности;
• развитие умения слушать и объяснять ход решения.

Воспитательные:

• воспитывать у учащихся навыки учебного труда;
• воспитывать культуру устной и письменной математической речи;
• воспитывать дружеское отношение в классе и умение работать в группах.

Тип урока: комбинированный.

Оборудование:

• Математика: учебник для 5 кл. общеобразоват. учреждений/ Н.Я. Виленкин, В.И. Жохов и др., М.: «Мнемозина», 2010.
• Карточки для групп учащихся с фигурами для вычисления площади сложной фигуры.
• Чертёжные инструменты.

План урока:

1. Организационный момент.
2. Актуализация знаний.
   а) Теоретические вопросы (тест).
   б) Постановка проблемы.
3. Изученного нового материала.
   а) поиск решения проблемы;
   б) решение поставленной проблемы.
4. Закрепление материала.
   а) коллективное решение задач;
   Физкультминутка.
   б) самостоятельная работа.
5. Домашнее задание.
6. Итог урока. Рефлексия.

Ход урока

I. Организационный момент.

Урок мы начнём вот с таких напутствующих слов:

Математика, друзья,
Абсолютно всем нужна.
На уроке работай старательно,
И успех тебя ждёт обязательно!

II. Актуализация знаний.

а) Фронтальная работа с сигнальными карточками (у каждого ученика карточки с числами 1, 2, 3, 4; при ответе на вопрос теста ученик поднимает карточку с номером правильного ответа).

1. Квадратный сантиметр – это:

1. площадь квадрата со стороной 1 см;
2. квадрат со стороной 1 см;
3. квадрат с периметром 1 см.

2. Площадь фигуры, изображённой на рисунке, равна:

1. 8 дм;
2. 8 дм²;
3. 15 дм².

3. Справедливо ли утверждение, что равные фигуры имеют равные периметры и равные площади?

1. да;
2. нет.

4. Площадь прямоугольника определяется по формуле:

1. S = a²;
2. S = 2 • (a + b);
3. S = a • b.

5. Площадь фигуры изображённой на рисунке, равна:

1. 12 см;
2. 8 см;
3. 16 см.

б) (Постановка проблемы). Задача. Сколько надо краски, чтобы покрасить пол, который имеет следующую форму (см. рис.), если на 1 м² расходуется 200 г краски?

III. Изучение нового материала.

Что же мы должны узнать, чтобы решить последнюю задачу? (Найти площадь пола, который имеет вид «сложной фигуры».)

Учащиеся формулируют тему и цели урока (если необходимо учитель помогает).

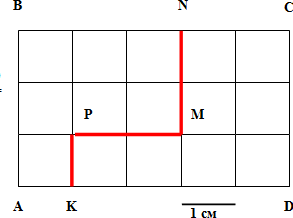
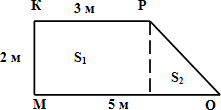
Рассмотрим прямоугольник ABCD. Проведём в нем линию KPMN, разбив прямоугольник ABCD на две части: ABNMPK и KPMNCD.

Чему равна площадь ABCD? (15 см²)

Чему равна площадь фигуры ABMNPK? (7 см²)

Чему равна площадь фигуры KPMNCD? (8 см²)

Проанализируйте полученные результаты. (15= = 7 + 8)

Вывод? (Площадь всей фигуры равна сумме площадей её частей.)

S = S₁ + S₂

Как можно применить это свойство для решения нашей задачи?(Разобьём сложную фигуру на части, найдём площади частей, затем площадь всей фигуры.)

S₁ = 7 • 2 = 14 (м²)
S₂ = (7 – 4) • (8 – 2 – 3) = 3 • 3 = 9 (м²)
S₃ = 7 • 3 = 21 (м²)
S = S₁ + S₂ + S₃ = 14 + 9 + 21 = 44 (м²)

Давайте составим план решения задач на нахождение площади «сложной фигуры»:

1. Разбиваем фигуру на простые фигуры.
2. Находим площади простых фигур.

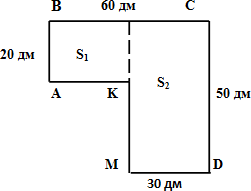
а) Задача 1. (коллективное решение на доске и в тетрадях.) Сколько потребуется плитки, чтобы выложить площадку следующих размеров:

Решение:

S = S₁ + S₂
S₁ = (60 – 30) • 20 = 600 (дм²)
S₂ = 30 • 50 = 1500 (дм²)
S = 600 + 1500 = 2100 (дм²)

Есть ли другой способ решения? (Рассматриваем предложенные варианты.)

Ответ: 2100 дм².

Задача 2. (коллективное решение на доске и в тетрадях.) Сколько требуется м² линолеума для ремонта комнаты, имеющей следующую форму:

Решение:

S = S₁ + S₂
S₁ = 3 • 2 = 6 (м²)
S₂ = ((5 – 3) • 2) : 2 = 2 (м²)
S = 6 + 2 = 8 (м²)

Ответ: 8 м².

Физкультминутка.

А теперь, ребята, встали.
Быстро руки вверх подняли.
В стороны, вперед, назад.
Повернулись вправо, влево.
Тихо сели, вновь за дело.

б) Самостоятельная работа (обучающего характера).

Учащиеся разбиваются на группы (№ 5–8 более сильные). Каждая группа – ремонтная бригада.

Задание бригадам: определите, сколько надо краски, чтобы покрасить пол, имеющий форму фигуры, изображённой на карточке, если на 1 м² требуется 200 г краски.

Вы эту фигуру строите своей тетради и записывая все данные, приступаете к выполнению задания. Можете обсуждать решение (но только в своей группе!). Если какая-то группа справляется с заданием быстро, то ей – дополнительное задание (после проверки самостоятельной работы).

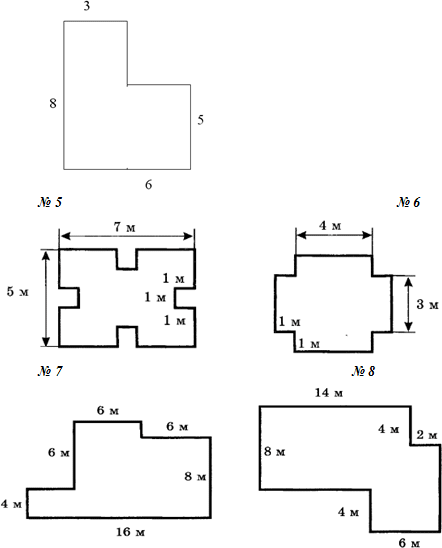
Задания для групп:

V. Домашнее задание.

п. 18, № 718, № 749.

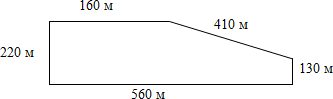
Дополнительное задание. План-схема Летнего сада (Санкт-Петербург). Вычислить его площадь.

VI. Итоги урока.

Рефлексия. Продолжи фразу:

• Сегодня я узнал…
• Было интересно…
• Было трудно…
• Теперь я могу…
• Урок дал мне для жизни…