Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
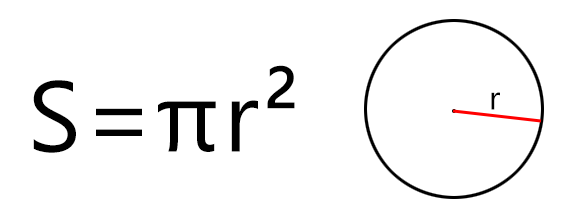
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):
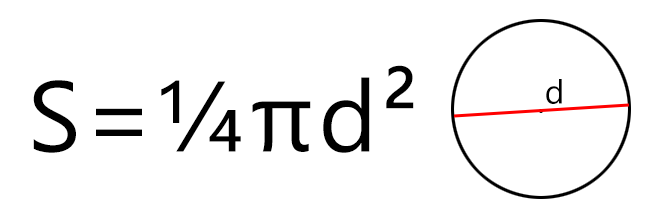
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):
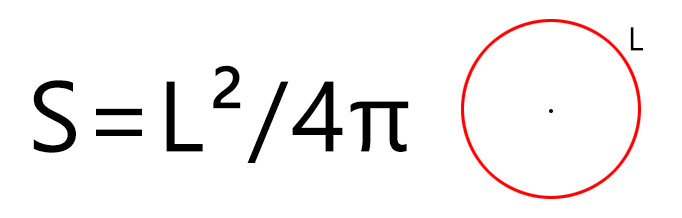
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
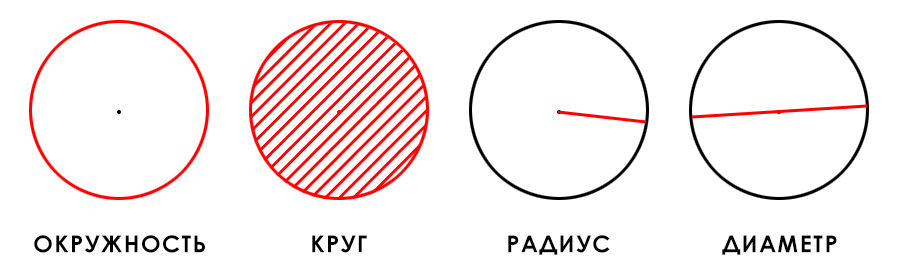
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:

Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
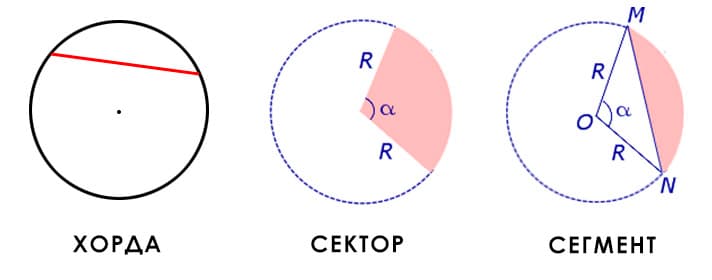
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
When you first start calculating area, you get easy shapes that have clearly defined formulas for finding their area: circles, triangles, squares and rectangles, for example. But what happens when you’re faced with a shape that doesn’t fit easily into those categories? Until you enter the brave new world of calculus integrals, the best way to find the area of irregular shapes is by subdividing them into shapes you’re already familiar with.
TL;DR (Too Long; Didn’t Read)
The simplest way to calculate the area of an irregular shape is to subdivide it into familiar shapes, calculate the area of the familiar shapes, then total those area calculations to get the area of the irregular shape they make up.
-
Note how you carry the units of measure – in this case, inches – throughout the calculations. Always write down your units of measure. Failing to do so is one of the most common errors but also one of the easiest to avoid.
-
Instead of subdividing the irregular shape into something familiar, can you add a piece to make it something familiar? For example, imagine that your shape looks like a square but with one corner cut off at an angle. Can you “add” a triangle to that cut-off corner to make it back into a tidy square? If yes, you can calculate the area of the entire square, then subtract the area of the triangle you just added in. The result will be the area of the irregular shape you started with.
Collect the area formulas for shapes you’re already familiar with. The most common shapes and their formulas include:
text{Area of a square or rectangle } = l × w
where l is length and w is width.
text{Area of a triangle } = frac{1}{2}(b × h)
where b is the triangle’s base and h is its vertical height.
text{Area of a parallelogram } = b × h
where b is the parallelogram’s base and h is its vertical height.
text{Area of a circle } = πr^2
where r is the radius of the circle.
Use your imagination to subdivide the irregular shape you have into more familiar shapes. Sometimes drawing the shape out, then adding lines for the subdivisions, helps you visualize it, and track the appropriate measurements for each dimension. For example, imagine that you have to find the area of a five-sided shape that isn’t a hexagon but has three perpendicular sides opposite the “point.” With a little thinking, you can subdivide this into a rectangle that butts up against a triangle, with the triangle forming the “point” of the shape.
Refer back to your area formulas for the dimensions you’ll need to calculate the area of each subdivided shape. In this case, you’ll need the base and vertical height of the triangle and the length and width (or two adjacent sides) of the rectangle. If you’re working a math problem in school, you’ll probably get at least some of these measurements and may need to use some basic algebra or geometry to find any missing measurements. If you’re working in the real world, you might be able to fill in some of the dimensions by physically measuring.
Fill the dimensions into the area formula for each subdivided shape. For example, if the triangle has a base of 6 inches and a vertical height of 3 inches, its area formula is:
frac{1}{2}(b × h) = frac{1}{2} (6 text{ in} × 3 text{ in}) = frac{1}{2} (18 text{ in}^2) = 9 text{ in}^2
If the rectangle has a length of 6 inches (which is also the side that makes up the base of the triangle) and a height of 4 inches, its area formula is:
l × w = 6 text{ in} × 4 text{ in} = 24 text{ in}^2
Tips
Add the areas of the subdivided shapes; the total is the area of the irregular shape you started with. To conclude this example, the area of the triangle is 9 in2, and the area of the rectangle is 24 in2. So your total area is:
9 text{ in}^2 + 24 text{ in}^2 = 33 text{ in}^2
Tips
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
Формула для нахождения площади круга через радиус:
π – константа равная (3.14); r – радиус круга.
Через диаметр
Формула для нахождения площади круга через диаметр:
π – константа равная (3.14); d – диаметр.
Через длину окружности

Формула для нахождения площади круга через длину окружности:
π – константа равная (3.14); l – длина окружности.
Площадь сегмента круга
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь сегмента круга
Чтобы посчитать площадь сегмента круга воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
По углу и радиусу

Угол α =
Радиус r =
Площадь сегмента круга
Sск =
0
Округление ответа: Округление числа π:
По длине хорды и высоте сегмента
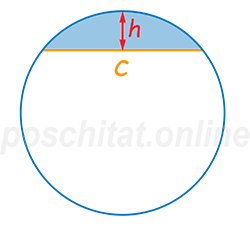
Хорда c =
Высота сегмента h =
Площадь сегмента круга
Sск =
0
Округление ответа:
По высоте и радиусу (или диаметру)

=
Высота сегмента h =
Площадь сегмента круга
Sск =
0
Округление ответа:
Просто введите данные и получите ответ.
Теория
Площадь сегмента окружности через угол и радиус
Чему равна площадь сегмента окружности Sск, если её радиус r, а угол сегмента α ?
Формула
В градусах:
Sск = r²2 ⋅ (π ⋅ α180° – sin α)
В радианах:
Sск = r²2 ⋅ (α – sin α)
Пример
К примеру, посчитаем площадь сегмента круга, имеющего радиус r = 2 см, а угол сегмента ∠α = 45°:
Sск = 2²2 ⋅ (3.14 ⋅ 45180 – sin 45) = 2 ⋅ (0.785 – 0.707) = 0.156 см²
Площадь сегмента окружности через хорду и высоту сегмента
Чему равна площадь сегмента окружности Sск, если длина хорды c, а высота сегмента h ?
Чтобы посчитать площадь сегмента, нам для начала потребуется вычислить радиус окружности r и угол сегмента α. А затем воспользоваться формулой площади сегмента из предыдущего параграфа.
Формула
Радиус круга:
r = c² + 4h²8h
Угол сегмента:
∠α = 2 ⋅ arcsinc2r
Пример
К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 2 см и длину хорды c = 5 см:
r = 5² + 4⋅2²8⋅2 = 25 + 1616 = 2.5625 см∠α = 2 ⋅ arcsin52 ⋅ 2.5625 = 2 ⋅ arcsin 0.9756 ≈ 2.7 radSск = 2.5625²2 ⋅ (2.7 – sin 2.7) = 3.2832 ⋅ (2.7 – 0,427) = 7.46 см²
Площадь сегмента окружности через высоту и радиус (или диаметр)
Чему равна площадь сегмента окружности Sск, если его высота h, а радиус r ?
Если нам известен не радиус, а диаметр, то делим его на 2 и получаем радиус (r = d ÷ 2).
Далее нам остаётся определить угол сегмента α. А затем воспользоваться формулой площади сегмента, описанной выше.
Формула
Угол сегмента:
∠α = 2 ⋅ arccosr – hr
Пример
К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 1 см, а диаметр окружности d = 4 см:
r = 4 ÷ 2 = 2 см
∠α = 2 ⋅ arccos2 – 12 = 2 ⋅ arccos 0.5 = 2.094 radSск = 2²2 ⋅ (2.094 – sin 2.094) = 2 ⋅ (2.094 – 0.866) = 2.456 см²
См. также
Как найти площадь полукруга
Необходимость найти площадь полукруга или сектора возникает регулярно при проектировании архитектурных сооружений. Это может понадобиться и при расчете ткани, например, на рыцарский или мушкетерский плащ. В геометрии встречаются самые разные задания на вычисление этого параметра. В условиях может быть предложено определить площадь полкруга, построенного на определенной стороне треугольника или параллелепипеда. В этих случаях необходимы дополнительные вычисления.

Вам понадобится
- – радиус полуокружности;
- – линейка;
- – циркуль;
- – лист бумаги;
- – карандаш;
- – формула площади круга.
Инструкция
Постройте окружность с заданным радиусом. Центр ее обозначьте как О. Чтобы получить полукруг, достаточно провести через эту точку отрезок до пересечения с окружностью. Этот отрезок является диаметром данной окружности и равен двум ее радиусам. Вспомните, что такое окружность и что такое круг. Окружность – это линия, все точки которой удалены от центра на одинаковое расстояние. Круг – часть плоскости, ограниченная этой линией.
Вспомните формулу площади круга. Она равна квадрату радиуса, умноженному на постоянный коэффициент π, равный 3,14. То есть площадь круга выражается формулой S=πR2, где S – площадь, а R – радиус окружности. Вычислите площадь полукруга. Она равна половине площади круга, то есть S1= πR2/2.
В случае, когда вам в условиях дана только длина окружности, найдите сначала радиус. Длина окружности вычисляется по формуле P=2πR. Соответственно, чтобы найти радиус, необходимо длину окружности разделить на удвоенный коэффициент. Получается формула R=P/2π.
Полукруг можно представить и как сектор. Сектором называется часть круга, которая ограничена его двумя радиусами и дугой. Площадь сектора равна площади круга, умноженной на отношение центрального угла к полному углу окружности. То есть, в данном случае она выражается формулой S=π*R2*n°/360°. Угол сектора известен, он составляет 180°. Подставив его значение, вы снова получите ту же самую формулу – S1= πR2/2.
Обратите внимание
Встречаются задания, где угол дуги указан не в градусах, а в радианах. В этом случае необходимо воспользоваться формулой перевода Ar = Ad *π / 180°, где Ar — угол в радианах, а Ad — он же в градусах. Для вычисления площади полукруга это не особенно важно. Даже если вы представляете полукруг как сектор, в конечной формуле никаких градусов нет. Но это может оказаться нужным для вычисления площади сектора, имеющего другой центральный угол.
В некоторых задачах требуется найти площадь круга или полукруга, построенного на определенной стороне правильного или неправильного многоугольника. Без дополнительных построений в этом случае не обойтись. Необходимо разделить заданную фигуру на другие, параметры которых вам заданы или вы легко можете их найти. После этого вычислите нужную сторону, которая чаще всего и представляет собой диаметр круга или полукруга.
Источники:
- формула как найти площадь
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
