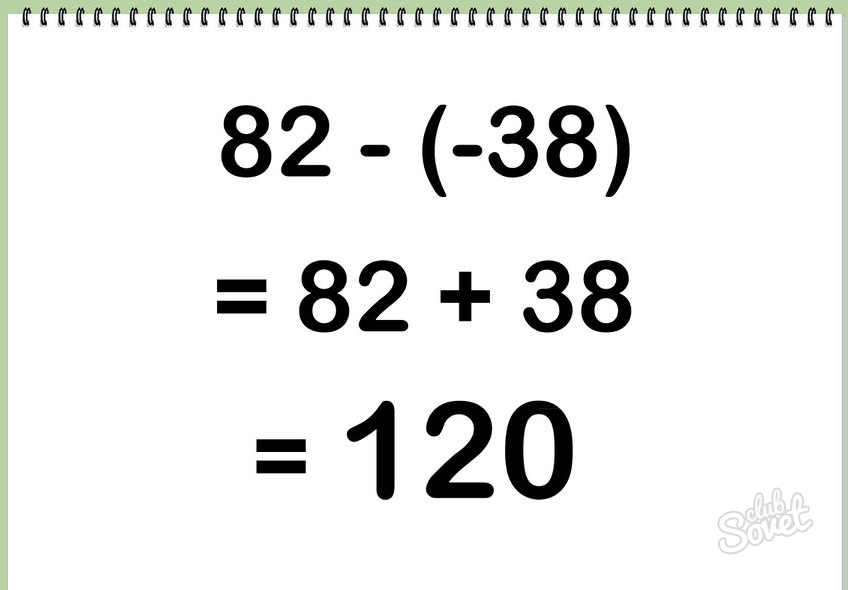как вычислить площадь неправильного многоугольника?
Мыслитель
(8599),
закрыт
15 лет назад
Дополнен 15 лет назад
программу надо написать
Донбасс
Знаток
(257)
15 лет назад
Разбить его на правильные фигуры S1,S2,…Sn. Вычислить по стандартным формулам.Потом сложить S1+S2+…+Sn=ПЛОЩАДЬ НЕПРВИЬНОГО МНОГОУГОЛЬНИКА.:)
Георгий НиколаевЗнаток (412)
3 года назад
Так не получится. Если многоугольник имеет вогнутые внутрь части, то при разбитии фигур будут получаться каждый раз новые фигуры. Я пробовал это с теоремой Герона. Но она действует только когда многоугольник полностью выпуклый- Герон дает точные результаты при суммировании треугольников. Ошибки начинаются, когда создаются самопересечения разбитых треугольников и ошибка растет в большую сторону.
Загрузить PDF
Загрузить PDF
Очень легко вычислить площадь правильного треугольника (это многоугольник!) и очень непросто сделать это в случае неправильного одиннадцатиугольника (это тоже многоугольник!). Данная статья расскажет вам, как вычислять площадь различных многоугольников.
-
1
Формула для нахождения площади правильного многоугольника: Площадь = 1/2 х периметр х апофема.
- Периметр – сумма сторон многоугольника.
- Апофема – отрезок, соединяющий центр многоугольника и середину любой из его сторон (апофема перпендикулярна стороне).
-
2
Найдите апофему. Она, как правило, дана в условии задачи. Например, дан шестиугольник, апофема которого равна 10√3.
-
3
Найдите периметр. Если периметр не дан в условии задачи, то его можно найти по известной апофеме.
- Шестиугольник можно разбить на 6 равносторонних треугольников. Апофема делит одну сторону пополам, создавая прямоугольный треугольник с углами 30-60-90 градусов.
- В прямоугольном треугольнике сторона, противолежащая углу в 60 градусов, равна x√3; углу в 30 градусов равна «х»; углу 90 градусов равна 2x. Если значение стороны x√3 равно 10√3, то х = 10.
- «х» – это половина длины основания треугольника. Удвойте ее и найдете полную длину основания. В нашем примере основание треугольника равно 20 единицам. В свою очередь основание треугольника есть сторона шестиугольника. Таким образом, периметр шестиугольника равен 20 х 6 = 120.
-
4
Подставьте значения апофемы и периметра в формулу. В нашем примере:
- площадь = 1/2 х 120 х 10√3
- площадь = 60 х 10√3
- площадь = 600√3
-
5
Упростите ответ. Возможно, вам придется записать ответ в виде десятичной дроби (то есть избавиться от корня). С помощью калькулятора найдите √3 и полученное число умножьте на 600: √3 х 600 = 1039,2. Это ваш окончательный ответ.
Реклама
-
1
Найдите площадь треугольника. Формула: Площадь = 1/2 х основание х высота.
- Если вам дан треугольник с основанием 10 и высотой 8, то его площадь = 1/2 х 8 х 10 = 40.
-
2
Найдите площадь квадрата. Чтобы найти площадь квадрата, просто возведите в квадрат длину одной его стороны. Если умножить основание квадрата на его высоту, мы получим тот же ответ, так как основание и высота равны.
- Если сторона квадрата равна 6, то его площадь = 6 х 6 = 36.
-
3
-
4
Найдите площадь трапеции. Формула: Площадь = [(основание1 + основание2) х высота] / 2.
- Например, дана трапеция с основаниями 6 и 8 и высотой 10. Ее площадь = [(6 + 8)•10]/2 = (14 х 10)/2 = 140/2 = 70.
Реклама
-
1
Используйте координаты вершин неправильного многоугольника. Зная координаты вершин, можно определить площадь неправильного многоугольника.
-
2
Сделайте таблицу. Запишите координаты вершин (х,у) (вершины выбирать последовательно в направлении против часовой стрелки). В конце списка еще раз напишите координату первой вершины.
-
3
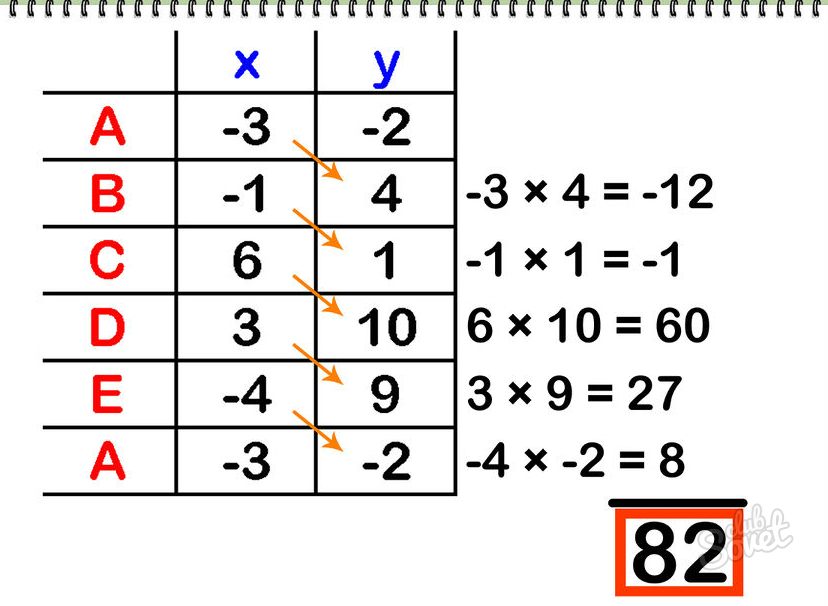
Умножьте значение координаты «х» первой вершины на значение координаты «у» второй вершины (и так далее). Сложите результаты (в нашем примере сумма равна 82).
-
4
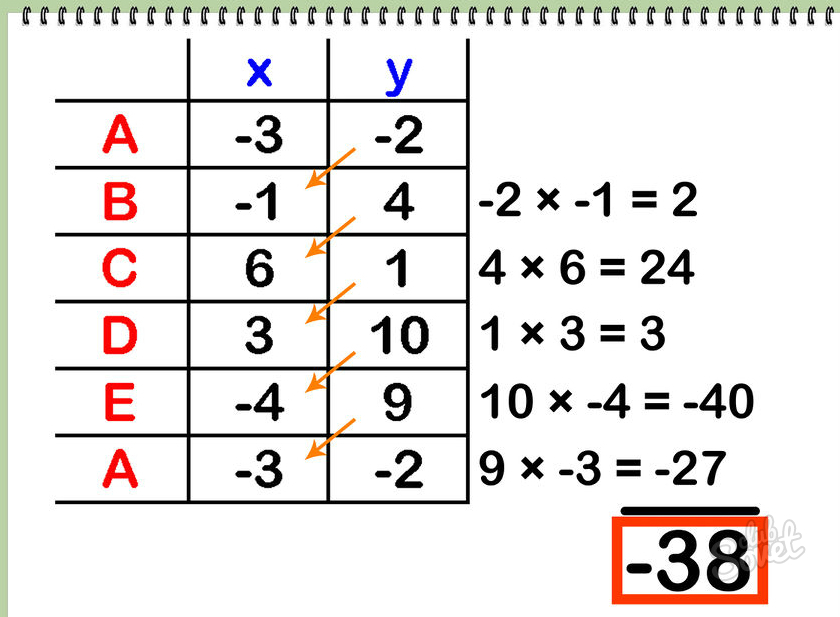
Умножьте значение координаты «у» первый вершины на значение координаты «х» второй вершины (и так далее). Сложите результаты (в нашем примере сумма равна -38).
-
5
Вычтите сумму, полученную в шаге 4, из суммы, полученной в шаге 3. В нашем примере: (82) – (-38) = 120.
-
6
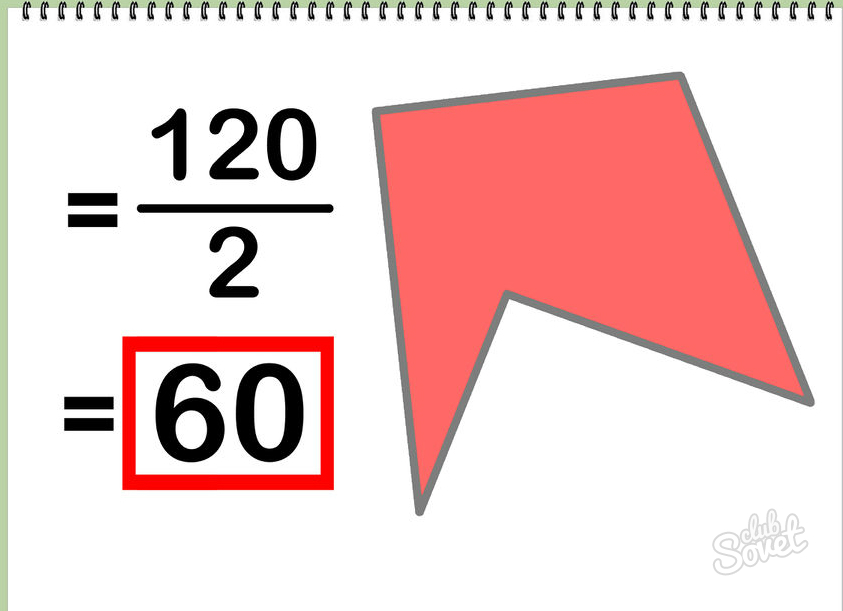
Разделите полученный результат на 2, чтобы найти площадь многоугольника: S=120/2 = 60 (квадратных единиц).
Реклама
Советы
- Если вы записываете координаты вершин в направлении по часовой стрелке, вы получите отрицательную площадь. Таким образом, это можно использовать для описания цикла или последовательности данного набора вершин, формирующих многоугольник.
- Данная формула находит площадь с учетом формы многоугольника. Если многоугольник имеет форму цифры 8, то необходимо из площади с вершинами против часовой стрелки вычесть площадь с вершинами по часовой стрелке.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 439 003 раза.
Была ли эта статья полезной?
Download Article
Download Article
Calculating the area of a polygon can be as simple as finding the area of a regular triangle or as complicated as finding the area of an irregular eleven-sided shape. If you want to know how to find the area of a variety of polygons, just follow these steps.
Area Help
-
1
Write down the formula for finding the area of a regular polygon. To find the area of a regular polygon, all you have to do is follow this simple formula: area = 1/2 x perimeter x apothem.[1]
Here is what it means:-
Perimeter = the sum of the lengths of all the sides[2]
- Apothem = a segment that joins the polygon’s center to the midpoint of any side that is perpendicular to that side[3]
-
Perimeter = the sum of the lengths of all the sides[2]
-
2
Find the apothem of the polygon. If you’re using the apothem method, then the apothem will be provided for you. Let’s say you’re working with a hexagon that has an apothem with a length of 10√3.
Advertisement
-
3
Find the perimeter of the polygon. If the perimeter is provided for you, then you’re nearly done, but it’s likely that you have a bit more work to do. If the apothem is provided for you and you know that you’re working with a regular polygon, then you can use it to find the perimeter. Here’s how you do it:[4]
- Think of the apothem as being the “x√3” side of a 30-60-90 triangle. You can think of it this way because the hexagon is made up of six equilateral triangles. The apothem cuts one of them in half, creating a triangle with 30-60-90 degree angles.
- You know that the side across from the 60 degree angle has length = x√3, the side across from the 30 degree angle has length = x, and the side across from the 90 degree angle has length = 2x. If 10√3 represents “x√3,” then you can see that x = 10.
- You know that x = half the length of the bottom side of the triangle. Double it to get the full length. The bottom side of the triangle is 20 units long. There are six of these sides to the hexagon, so multiply 20 x 6 to get 120, the perimeter of the hexagon.
-
4
Plug the apothem and the perimeter into the formula. If you’re using the formula area = 1/2 x perimeter x apothem, then you can plug in 120 for the perimeter and 10√3 for the apothem. Here is what it will look like:[5]
- area = 1/2 x 120 x 10√3
- area = 60 x 10√3
- area = 600√3
-
5
Simplify your answer. You may need to state your answer in decimal instead of square root form. Just use your calculator to find the closest value for √3 and multiply it by 600. √3 x 600 = 1,039.2. This is your final answer.[6]
Advertisement
-
1
Find the area of a regular triangle. If you want to find the area of a regular triangle, all you have to do is follow this formula: area = 1/2 x base x height.
- If you have a triangle with a base of 10 and a height of 8, then the area = 1/2 x 8 x 10, or 40.
-
2
Find the area of a square. To find the area of a square, just square the length of one side. This is really the same thing as multiplying the base of the square by its height, because the base and height are the same.
- If the square has a side length of 6, then the area is 6 x 6, or 36.
-
3
Find the area of a rectangle. To find the area of a rectangle, simply multiply the base times the height.
- If the base of the rectangle is 4 and the height is 3, then the area of the rectangle is 4 x 3, or 12.
-
4
Find the area of a trapezoid. The find the area of a trapezoid, you just have to follow this formula: area = [(base 1 + base 2) x height]/2.
- Let’s say you have a trapezoid with bases that have a length of 6 and 8 and a height of 10. The area is simple [(6 + 8) x 10]/2, which can be simplified to (14 x 10)/2, or 140/2, which makes for an area of 70.
Advertisement
-
1
Write down the coordinates of the vertices[7]
of the irregular polygon. Determining the area for an irregular polygon can be found when you know the coordinates of the vertices.[8]
-
2
Create an array. List the x and y coordinates of each vertex of the polygon in counterclockwise order. Repeat the coordinates of the first point at the bottom of the list.[9]
-
3
Multiply the x coordinate of each vertex by the y coordinate of the next vertex. Add the results. The added sum of these products is 82.
-
4
Multiply the y coordinate of each vertex by the x coordinate of the next vertex. Again, add these results. The added total of these products is -38.
-
5
Subtract the sum of the second products from the sum of the first products. Subtract -38 from 82 to get 82 – (-38) = 120.
-
6
Divide this difference by 2 to get the area of the polygon. Just divide 120 by 2 to get 60 and you’re all done.
Advertisement
Add New Question
-
Question
How can I calculate the area of an irregular polygon?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
Divide the polygon into several triangles. Then, calculate the area of each triangle by multiplying the base by half of the height. Add the different areas together to find the total area of the polygon.
-
Question
How do I calculate the area of an octagon?
Cut it into smaller shapes, such as triangles or other quadrilaterals using angles. Find the area of each smaller shape, then add the areas together to find the area of the whole shape.
-
Question
How do I find the area of a 4-sided shape?
Assuming it’s not a square or rectangle, you would have to subdivide the figure into smaller sections consisting of squares, rectangles, triangles, and other shapes whose areas can be easily calculated. Then add those areas together.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
If you list the points in a clockwise order instead of counterclockwise, you will get the negative of the area. Hence this can be used as a tool to identify the cyclic path or sequence of a given set of points forming a polygon.
-
This formula computes area with orientation. If you use it on a shape where two of the lines cross like a figure eight, you will get the area surrounded counterclockwise minus the area surrounded clockwise.
Advertisement
References
About This Article
Article SummaryX
A polygon is any kind of closed, 2-dimensional shape with at least 3 straight sides and no curves. If a polygon is regular—that is, all of its sides are the same length—you can easily find the area given the side length and the apothem. The apothem is the distance from the exact center of the polygon to the center of any of the sides. If you know the apothem and the side length, simply use the formula area = ½ x perimeter x apothem. You can find the perimeter by adding together the lengths of all the sides, or multiplying the length of a side by the number of sides. For example, say you have a hexagon with an apothem that has a length of 3 units, and each side has a length of 7 units. Multiply 7 by 6 (the number of sides in the hexagon) to find the perimeter of 42 units. Multiply 42 x 3 x ½ to get an area of 63 square units. Some types of polygons have their own special formulas that you can use to find the area. For instance, to calculate the area of a triangle, use the formula ½ x base x height. For a rectangle, all you need to do is multiply length times width. Since the length and width are the same for a square, simply square the length of one of the sides to calculate the area. If your shape is a trapezoid, add together the lengths of the two parallel sides, then multiply the sum by the height of the trapezoid. Divide the result by 2 to get the area. In other words, use the formula area = (base1 + base2) x h x ½. When you’re dealing with an irregular polygon, things get a little trickier. The easiest way to find the area of an irregular polygon is to plot it on a graph and find the coordinates of each of the vertices, or corners. Create a table with the x-coordinate of each vertex in one column, and the y-coordinate of each vertex in the next column. Multiply the x-coordinate of each vertex by the y-coordinate of the vertex below it in the table and add all the products together. Then go back the other way, and multiply each y-coordinate by the x-coordinate below it. Add together those products as well. Subtract the sum of the second set of products from the sum of the first set, then divide the difference by 2 to find the area of the polygon. If you need to calculate the area of an irregularly-shaped polygon, keep reading to learn how!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,466,230 times.
Reader Success Stories
-
Olexiy Korshunov
Aug 14, 2019
“The calculation of the area of an irregular polygons is very intelligibly written and is easily implemented for…” more
Did this article help you?
Как найти площадь многоугольника
Все, что имеет больше двух углов, является многоугольником, в том числе и треугольник. Рассмотрим, как найти площадь многоугольников.
1
Как найти площадь многоугольника – треугольник
- S = 1/2×h×b, где h – высота, а b – сторона.
- S = 1/2 a×b×sinα, где а и b – стороны треугольника, а sinα – синус угла между ними.
- S = √p×(p-a)×(p-b)×(p-c), где p – половина периметра, а, b, c – стороны. Если известны все стороны треугольника, то найти площадь можно именно по этой формуле.
- S = r×p, где r – радиус вписанной окружности, а p – половина периметра. Если в треугольник вписана окружность, то для нахождения площади можно использовать эту формулу.
- S = abc/4R, где a, b, c – стороны треугольника, а R – радиус описанной окружности. Если треугольник вписан в окружность, для нахождения площади треугольника можно использовать эту формулу.
Прямоугольный треугольник
- S = 1/2×ab, где a и b – катеты прямоугольного треугольника.
- S = d×e, где d и e отрезки гипотенузы, образованные при касании вписанной окружности об гипотенузу.
- S = (p-a)×(p-b), где p – половина периметра, а и b – катеты.
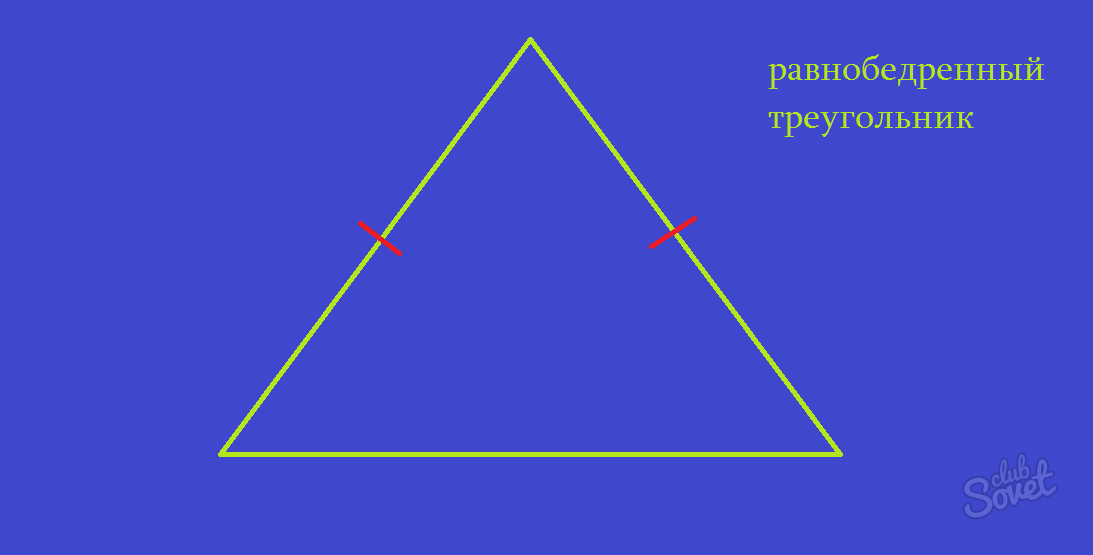
Равнобедренный треугольник
- S = 1/2×a²×sina, где а – бедро треугольника, sina же – угол между бедрами.
- S = b²/4tgα/2, где b – основание треугольника, а tgα – угол между бедрами.
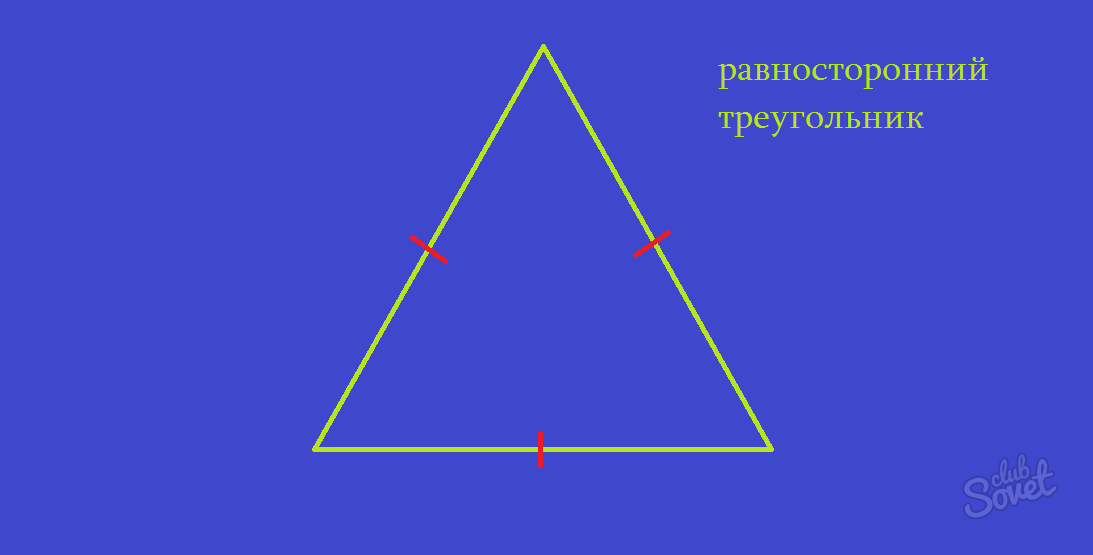
Равносторонний треугольник
- S = √3×a²/4, где а – сторона треугольника (любая, так как в равностороннем треугольнике все стороны равны).
- S = 3√3×R²/4, где R – радиус окружности, в которую вписан треугольник.
- S = 3√3×r², где r – радиус окружности, которая вписана в треугольник.
- S = h²/√3, где h – высота равностороннего треугольника.
2
Как найти площадь многоугольника – квадрат
- S = a², а – сторона квадрата. Так как все стороны квадрата равны, достаточно умножить одну его сторону на другую.
- S = d²/2, где d – диагональ квадрата.
3
Как найти площадь многоугольника – прямоугольник
- S = a×b, где a и b – стороны прямоугольника. Так как противолежащие стороны в прямоугольнике равны, достаточно умножить одну его сторону (длину) на не противолежащую, перпендикулярную сторону (ширину).
- S = a²+b²=c², где a – ширина, b – длина, а c – диагональ. Диагональ делит прямоугольник на два прямоугольных треугольника и если в условии задачи дана одна сторона прямоугольника и его диагональ, несложно будет найти и третью сторону, использую теорему Пифагора. После того как мы найдем эту сторону, ищем площадь по стандартной формуле a×b. Пример: Ширина прямоугольника – 3см, диагональ – 5 см. Найти площадь. Пишем 3² + x² = 5². x² = 16 => x = 4. S = a×b = 3×4=12. Ответ: S прямоугольника = 12см²
4
Как найти площадь многоугольника – трапеция
- S = (a+b)×h/2, где a – маленькое, b – большое основание трапеции, h – высота.
- S = h×m, где h – высота, m – средняя линия трапеции, равная половине суммы оснований – 1/2×(a+b).
- S = 1/2×d1×d2×sinα, где d1 и d2 – диагонали трапеции, а sinα – синус угла между ними.
- S = a+b/2×√c²-((b-a)²+c²-d²/2(b-a))², где a и b – основания трапеции, c и d – остальные две стороны.
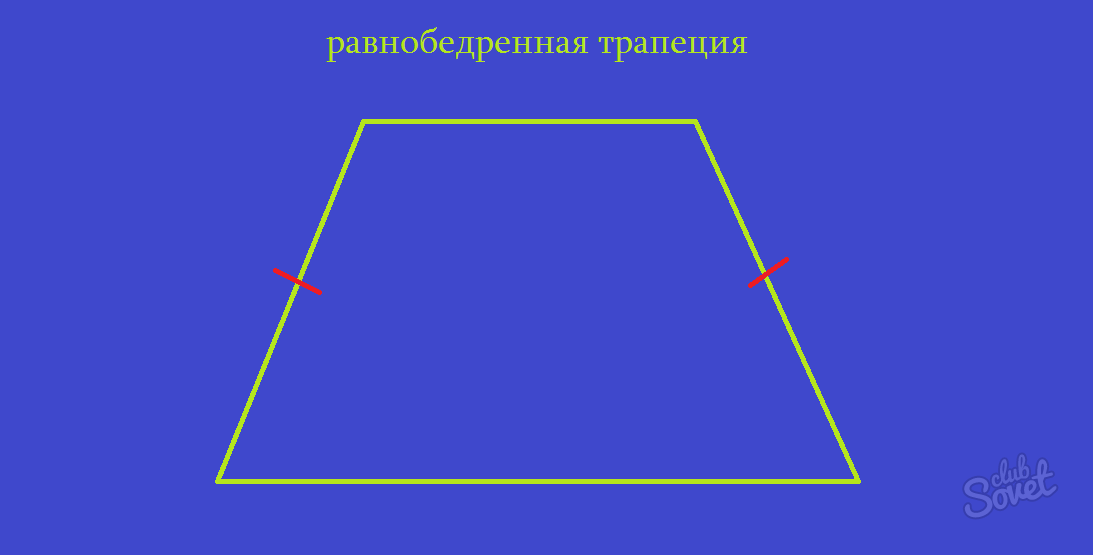
Равнобедренная трапеция
S = 4r²/sinα, где r – радиус вписанной окружности, а sinα – синус угла между стороной и основанием.
5
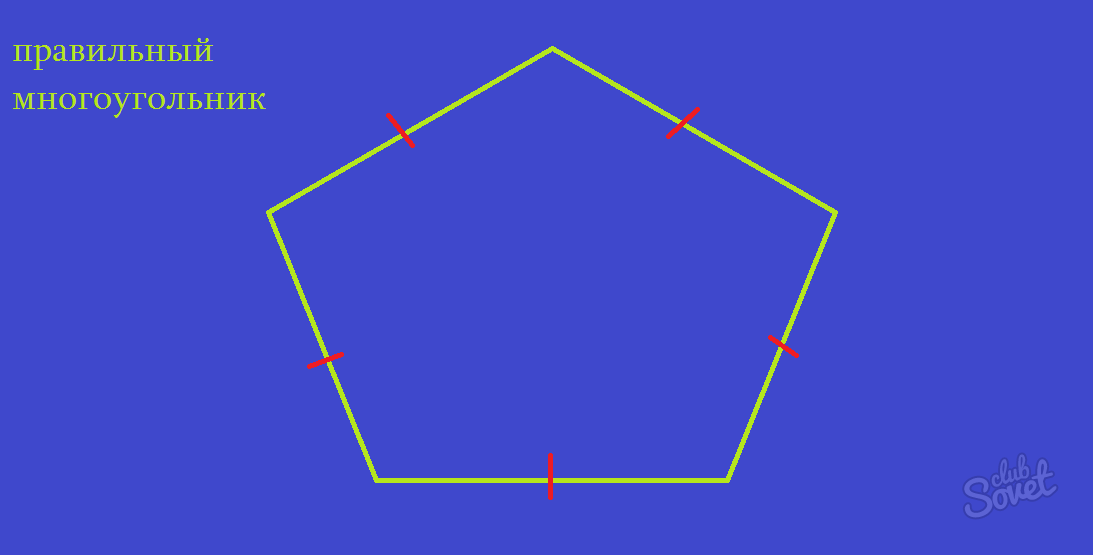
Площадь правильного многоугольника
- S = r×p = 1/2×r×n×a, где r – радиус вписанной окружности, p – половина периметра. Для того чтобы найти площадь любого правильного многоугольника, нужно разбить его на равные треугольники с общей вершиной в центре вписанной окружности.
- S = n×a²/4tg(360°/2n), где n – число сторон правильного многоугольника, а – длина стороны.
Также вычислить площадь правильного многоугольника поможет данный онлайн сервис. Просто вставьте нужное значение и получите ответ.
6
Площадь неправильного многоугольника
Площадь неправильного многоугольника можно найти с помощью координат его вершин. Если в условии задачи даны вышеупомянутые координаты, то выполняем следующее:
- Составляем таблицу указывая букву, обозначающую вершину и соответствующие координаты (x; y).
- Умножаем значение x одной вершины на значение y второй и так далее.
- Складываем все значение, получаем какое-то число.
- Составляем точно такую таблицу, по такому же принципу умножаем y координату одной вершины на x координату второй, складываем получившиеся значения.
- От суммы значений первой таблицы отнимаем сумму значений второй таблицы.
- Полученное число делим на 2 и тем самым находим площадь неправильного многоугольника.
Как вычислить площадь неправильного многоугольника зная периметр?
Формула для нахождения площади правильного многоугольника: Площадь = 1/2 х периметр х апофема.
- Периметр – сумма сторон многоугольника.
- Апофема – отрезок, соединяющий центр многоугольника и середину любой из его сторон (апофема перпендикулярна стороне).
Как найти площадь неправильного треугольника?
Площадь треугольника через гипотенузу и по радиусу вписанной окружности. S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.
Как найти площадь треугольника если известны все его стороны?
h = 2/a √p(p-a)(p-b)(p-c), где h – длина высоты треугольника, p – полупериметр, a – длина стороны, на которую падает высота (основание), b и c – длины двух других сторон треугольника.
Как высчитать квадратуру треугольника?
что обозначает, что площадь треугольника равна произведению длины его основания и высоты поделенной на два.
Как считается площадь?
В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах. Формула по которой можно высчитать площадь: S комнаты = А х B, где A – длина, B – ширина.
Как посчитать Площу Трикутника?
Формула Герона Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Как найти площадь равностороннего треугольника 4 класс?
Многоугольник, который имеет три вершины и три стороны, называется треугольником. Треугольник называется равносторонним, если все его три стороны равны. Площадь равностороннего треугольника вычисляется как половина как половина произведения его основания на высоту.
Как найти высоту равностороннего треугольника зная сторону?
Если подставить вместо угла альфа 60 градусов, получится, что высота равностороннего треугольника равна половине стороны, умноженной на корень из трех.
Как найти высоту равностороннего треугольника?
Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами «а» и «b» гипотенуза «с» равна: a2+b2=c2. Эту теорему можно использовать, чтобы найти высоту равностороннего треугольника! Разделите равносторонний треугольник на два прямоугольных треугольника (для этого проведите высоту).
Как найти высоту треугольника через площадь?
С другой стороны та же площадь треугольника через высоту равна половине произведения стороны треугольника на высоту, на нее опущенную. Отсюда высота будет равна отношению удвоенной площади к стороне треугольника. Из предыдущей формулы можно выразить площадь через три стороны треугольника и заменить ее в формуле высоты.
Как найти высоту треугольника 7 класс?
из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней (перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90 ° ) — это и будет высота. Так же как медианы и биссектрисы, треугольник имеет три высоты. Высоты треугольника пересекаются в одной точке.
Как вычислить высоту треугольника если известны стороны?
В зависимости от входных данных, высоту треугольника можно найти разными способами. h = 2/a √p(p-a)(p-b)(p-c), где h – длина высоты треугольника, p – полупериметр, a – длина стороны, на которую падает высота (основание), b и c – длины двух других сторон треугольника.
Как найти H в треугольнике?
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
- H – высота треугольника
- p – полупериметр, p=(a+b+c)/2.
- R – радиус описанной окружности
Чему равна высота в треугольнике?
Высота в формулах обозначается буквой h, нижний индекс которой соответствует стороне, на которую она опущена. Пояснения к формулам. Высота треугольника равна частному от деления произведения сторон, прилежащих к углу, из которого опущена эта высота, на удвоенный радиус описанной вокруг него окружности (Формула 4).
Как определить наибольшую высоту в треугольнике?
Чтобы найти наибольшую высоту треугольника, можно площадь треугольника разделить на длину стороны, к которой проведена эта высота (то есть на длину наименьшей из сторон треугольника).
Как найти площадь параллелограмма по высоте?
Площадь параллелограмма, формула. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h): 1.
Как найти вторую высоту у параллелограмма?
высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей стороны и отсекаемой высотой части основания. Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 3 см, то длина высоты будет: h=?(5^2-3^2)=4 (см).
Как найти периметр параллелограмма зная одну сторону и высоту?
Формулы определения длины периметра параллелограмма:
- Формула периметра параллелограмма через стороны параллелограмма: P = 2a + 2b = 2(a + b)
- Формула периметра параллелограмма через одну сторону и две диагонали: P = 2a + √2d12 + 2d22 – 4a2 …
- Формула периметра параллелограмма через одну сторону, высоту и синус угла: