Как рассчитать площадь ромба
На данной странице калькулятор поможет рассчитать площадь ромба онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
Через сторону и высоту
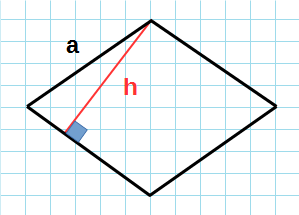
Формула для нахождения площади ромба через сторону и высоту:
a – сторона ромба; h – высота ромба.
Через диагонали
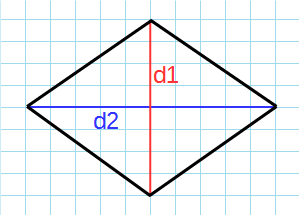
Формула для нахождения площади ромба через диагонали:
d1, d2 – диагонали ромба.
Через сторону и угол
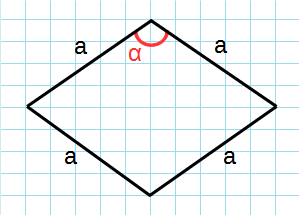
Формула для нахождения площади ромба через сторону и угол:
a – сторона ромба; α – угол между сторонами.
Через угол и диагональ из этого угла
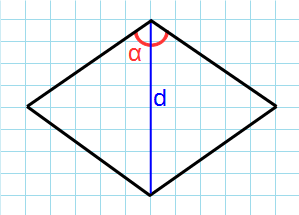
Формула для нахождения площади ромба через угол и диагональ выходящая из этого угла:
d – диагональ ромба; α – угол между сторонами.
Через угол и противолежащию диагональ
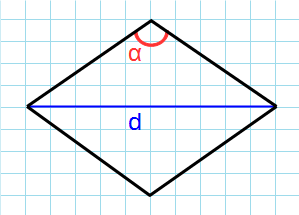
Формула для нахождения площади ромба через угол и диагональ противолежащая углу:
d – диагональ ромба; α – угол между сторонами.
Через угол и радиус вписанной окружности
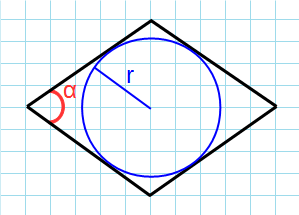
Формула для нахождения площади ромба через угол и радиус вписанной окружности:
r – радиус окружности; α – угол между сторонами.
Через сторону и радиус вписанной окружности
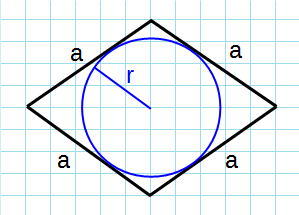
Формула для нахождения площади ромба через сторону и радиус вписанной окружности:
a – сторона ромба; r – радиус вписанной окружности.
Математика — школьный предмет, который изучается всеми, независимо от профиля класса. Однако она не всеми любима. Порой незаслуженно. Эта наука постоянно подбрасывает ученикам задачи, которые позволяют их мозгу развиваться. Математика отлично справляется с тем, чтобы не дать мыслительным возможностям детей угаснуть. Особенно хорошо с этим справляется один из ее разделов – геометрия.
Любая из тем, которые в ней изучаются, достойна внимания и уважения. Геометрия — это способ развить пространственное воображение. Примером может служить тема о площадях фигур, в частности ромбов. Эти задачки могут завести в тупик, если не разобраться в деталях. Потому что возможны разные подходы к поиску ответа. Кому-то проще запомнить разные варианты формул, которые написаны ниже, а кто-то способен сам их получить из ранее усвоенного материала. В любом случае безвыходных ситуаций не бывает. Если немного подумать, то решение обязательно найдется.
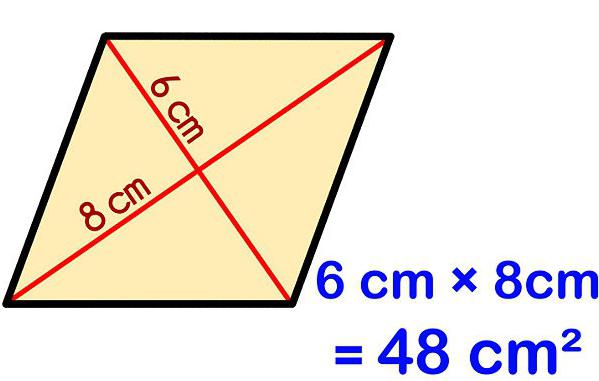
Что такое ромб и чем он похож на другие четырехугольники?
Ответить на этот вопрос нужно, чтобы понять принципы получения формул и ход рассуждения в задачах. Ведь чтобы разобраться в том, как найти площадь ромба, нужно отчетливо понимать, что это за фигура и каковы ее свойства.
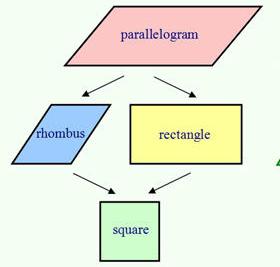
Для удобства рассмотрения параллелограмм, который является четырехугольником с попарно параллельными сторонами, примем за “родителя”. У него есть двое “детей”: прямоугольник и ромб. Оба они являются параллелограммами. Если продолжать параллели, то это – “фамилия”. Значит, для того чтобы найти площадь ромба, можно воспользоваться уже изученной формулой для параллелограмма.
Но, как и все дети, ромб имеет и нечто свое. Это немного отличает его от “родителя” и позволяет рассматривать как отдельную фигуру. Ведь прямоугольник не ромб. Возвращаясь к параллелям – они как брат и сестра. В них много общего, но они все же различаются. Эти отличия — их особенные свойства, которыми нужно пользоваться. Было бы странно знать о них и не применять в решении задач.
Если продолжить аналогии и вспомнить еще одну фигуру – квадрат, то она будет продолжением ромба и прямоугольника. В этой фигуре объединены все свойства и одного, и другого.
Свойства ромба
Их пять и они перечислены ниже. Причем некоторые из них повторяют свойства параллелограмма, а какие-то присущи только рассматриваемой фигуре.
- Ромб — это параллелограмм, который принял особую форму. Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата.
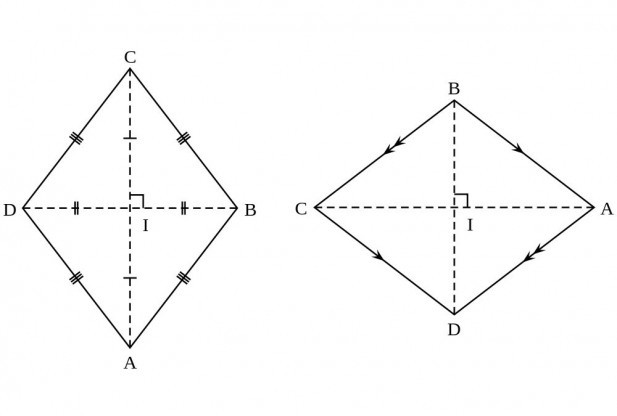
- Диагонали этого четырехугольника пересекаются под углом, который равен 90º. Это удобно и во многом упрощает ход рассуждений при решении задач.
- Другое свойство диагоналей: каждая из них делится точкой пересечения на равные отрезки.
- Лежащие друг напротив друга углы у этой фигуры равны.
- И последнее свойство: диагонали ромба совпадают с биссектрисами углов.
Обозначения, которые приняты в рассмотренных формулах
В математике полагается решать задачи с использованием общих буквенных выражений, которые называются формулами. Тема про площади не является исключением.
Для того чтобы перейти к записям, которые расскажут, как найти площадь ромба, нужно договориться о буквах, которыми заменены все числовые значения элементов фигуры.
|
Название элемента |
Обозначение |
|
сторона ромба |
а |
|
большая диагональ |
Д1 |
|
маленькая диагональ |
Д2 |
|
высота ромба |
Н |
|
острый угол |
А |
|
тупой угол |
В |
|
радиус вписанной в ромб окружности |
общепринятые в математике обозначения |
|
площадь фигуры |
Теперь пришла пора написания формул.
Среди данных задачи – только диагонали ромба
Правило утверждает, что для нахождения неизвестной величины нужно перемножить длины диагоналей, а потом произведение разделить пополам. Результат деления — это и есть площадь ромба через диагонали.
Формула для этого случая будет выглядеть так:
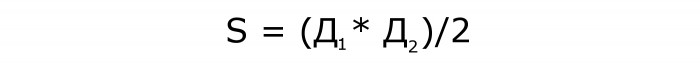
Пусть эта формула будет идти под номером 1.
В задаче даны сторона ромба и его высота
Чтобы вычислить площадь, потребуется найти произведение этих двух величин. Пожалуй, это самая простая формула. Причем она известна еще из темы про площадь параллелограмма. Там такая формула уже изучалась.
Математическая запись:
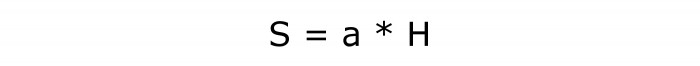
Номер этой формулы — 2.
Известны сторона и острый угол
В этом случае нужно возвести в квадрат величину стороны ромба. Потом найти синус угла. И третьим действием вычислить произведение двух образовавшихся величин. Ответом будет площадь ромба.
Буквенное выражение:
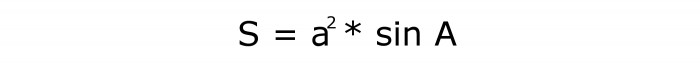
Его порядковый номер — 3.
Данные величины: радиус вписанной окружности и острый угол
Для вычисления площади ромба нужно найти квадрат радиуса и умножить его на 4. Определить значение синуса угла. Потом разделить произведение на вторую величину.
Формула принимает такой вид:
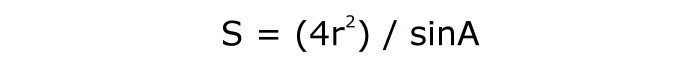
Она будет пронумерована цифрой 4.
В задаче фигурируют сторона и радиус вписанной окружности
Чтобы определить, как найти площадь ромба, потребуется вычислить произведение данных величин и числа 2.
Формула для этой задачи будет выглядеть так:
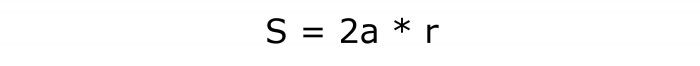
Ее номер по порядку — 5.
Примеры возможных заданий
Задача 1
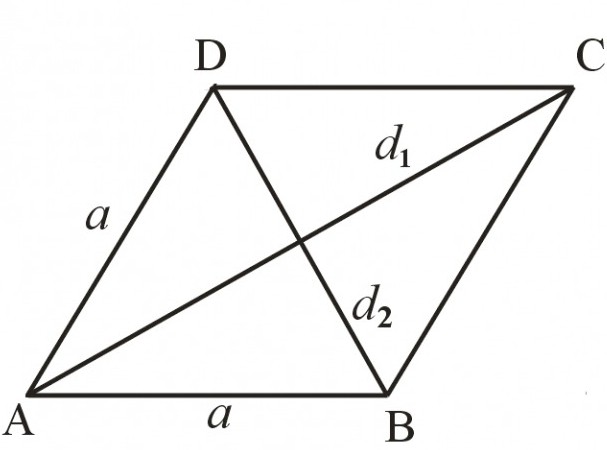
Одна из диагоналей ромба равна 8, а другая — 14 см. Требуется найти площадь фигуры и длину ее стороны.

Решение
Для нахождения первой величины потребуется формула 1, в которой Д1 = 8, Д2 = 14. Тогда площадь вычисляется так: (8 * 14) / 2 = 56 (см2).
Диагонали делят ромб на 4 треугольника. Каждый из них обязательно будет прямоугольным. Этим нужно воспользоваться, чтобы определить значение второй неизвестной. Сторона ромба станет гипотенузой треугольника, а катетами будут половины диагоналей.
Тогда а2 = (Д1 /2)2 + (Д2 /2) 2. После подстановки всех значений получается: а2 = (8 / 2)2 + (14 / 2)2 = 16 + 49 = 65. Но это квадрат стороны. Значит, нужно извлечь квадратный корень из 65. Тогда длина стороны будет приблизительно равна 8,06 см.
Ответ: площадь 56 см2, а сторона 8,06 см.
Задача 2
Сторона ромба имеет значение, равное 5,5 дм, а его высота — 3,5 дм. Найти площадь фигуры.
Решение
Для того чтобы найти ответ нужна будет формула 2. В ней а = 5,5, Н = 3,5. Тогда, заменив в формуле буквы на числа, получим, что искомая величина равна 5,5 * 3,5 = 19,25 (дм2).
Ответ: площадь ромба равна 19,25 дм2.
Задача 3
Острый угол у некоторого ромба равен 60º, а его меньшая диагональ — 12 см. Требуется вычислить его площадь.
Решение
Чтобы получить результат, нужна будет формула под номером 3. В ней вместо А будет 60, а значение а неизвестно.
Для нахождения стороны ромба потребуется вспомнить теорему синусов. В прямоугольном треугольнике а будет гипотенузой, меньший катет равен половине диагонали, а угол делится пополам (известно из свойства, где упоминается биссектриса).
Тогда сторона а будет равна произведению катета на синус угла.
Катет нужно вычислить как Д/2 = 12/2 = 6 (см). Синус(А/2) будет равен его значению для угла 30º, то есть 1/2.
Выполнив несложные вычисления, получим такое значение стороны ромба: а = 3 (см).
Теперь площадь — это произведение 32 и синуса 60º, то есть 9 * (√3)/2 = (9√3)/2 (см2).
Ответ: искомая величина равна (9√3)/2 см2.
Итоги: все возможно
Здесь были рассмотрены некоторые варианты того, как найти площадь ромба. Если в задаче напрямую непонятно, какую формулу использовать, то нужно немного подумать и попробовать связать ранее изученные темы. В других темах обязательно найдется подсказка, которая поможет связать известные величины с теми, что есть в формулах. И задача решится. Главное – помнить, что все раньше изученное можно и нужно использовать.
Кроме предложенных заданий, возможны и обратные задачи, когда по площади фигуры нужно вычислить значение какого-либо элемента ромба. Тогда нужно воспользоваться тем уравнением, которое ближе всего к условию. А потом преобразовать формулу, оставив в левой части равенства неизвестную величину.

{S = a^2 cdot sin (alpha)}
На этой странице мы предлагаем вам 7 формул площади ромба. Для каждой формулы можно воспользоваться онлайн калькулятором и мгновенно получить результат, не прибегая к помощи обычного калькулятора
Содержание:
- калькулятор площади ромба
- формула площади ромба через сторону и угол
- формула площади ромба через сторону и высоту
- формула площади ромба через диагонали
- формула площади ромба через угол и диагональ из угла
- формула площади ромба через угол и противолежащую диагональ
- формула площади ромба ромба через радиус вписанной окружности и угол
- формула площади ромба через радиус вписанной окружности и сторону
- примеры задач
Формула площади ромба через сторону и угол

S = a^2 cdot sin (alpha)
a – сторона ромба
α – угол между сторонами ромба
Формула площади ромба через сторону и высоту

S = a cdot h
a – сторона ромба
h – высота ромба
Формула площади ромба через диагонали
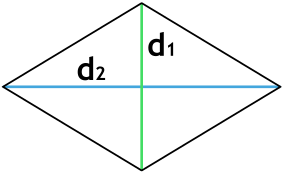
S = dfrac{d_1 cdot d_2}{2}
d1 и d2 – диагонали ромба
Формула площади ромба через угол и диагональ из угла
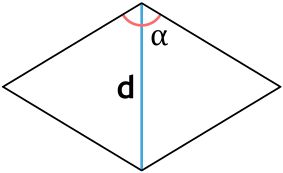
S = dfrac{d^2}{2} cdot \tg(dfrac{alpha}{2})
d – диагональ ромба
α – угол между сторонами ромба, из которого выходит диагональ
Формула площади ромба через угол и противолежащую диагональ

S = dfrac{d^2}{2} cdot ctg(dfrac{alpha}{2})
d – диагональ ромба, противоположная углу α
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и угол
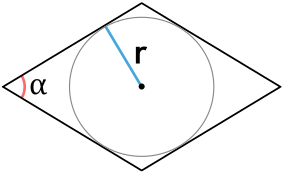
S = dfrac{4r^2}{sin(alpha)}
r – радиус окружности
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и сторону
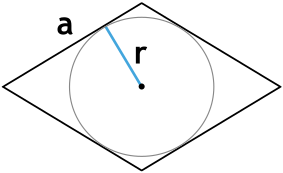
S = 2ar
r – радиус окружности
a – сторона ромба
Примеры задач на нахождение площади ромба
Задача 1
Найдите площадь ромба если его диагонали равны 34 и 4.
Решение
Для решения задачи воспользуемся формулой площади ромба через диагонали.
S = dfrac{d_1 cdot d_2}{2} = dfrac{34 cdot 4}{2} = 68 : см^2
Ответ: 68 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь ромба если его диагонали равны 4 и 6.
Решение
Задача аналогична предыдущей.
S = dfrac{d_1 cdot d_2}{2} = dfrac{4 cdot 6}{2} = 12 : см^2
Ответ: 12 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь ромба стороны которого равны 5, а высота равна 4.
Решение
Воспользуемся формулой площади ромба через высоту и сторону.
S = a cdot h = 5 cdot 4 = 20 : см^2
Ответ: 20 см²
Проверим полученный ответ на калькуляторе .
Так как ромб – это параллелограмм, у которого все стороны равны, то для него действуют все те же формулы, как и для параллелограмма, включая формулу нахождения площади через произведение высоты и стороны.
Площадь ромба можно найти, также зная его диагонали. Диагонали делят ромб на четыре абсолютно одинаковых прямоугольных треугольника. Если мы их рассортируем, так чтобы получить прямоугольник, то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).
Если в распоряжении только угол и сторона, то можно вооружиться диагональю в качестве помощника и начертить ее напротив известного угла. Тогда она разделит ромб на два конгруэнтных треугольника, площади которых в сумме дадут нам площадь ромба. Площадь каждого из треугольников будет равна половине произведения квадрата стороны на синус известного угла, как площадь равнобедренного треугольника. Поскольку таких треугольников два, то коэффициенты сокращаются, оставив только сторону во второй степени и синус:


Если внутри ромба вписать окружность, то его радиус будет относиться к стороне под углом 90°, что значит, что удвоенный радиус будет равен высоте ромба. Подставив вместо высоты h=2r в предыдущую формулу, получим площадь S=ha=2ra
Если же вместе с радиусом вписанной окружности, дана не сторона, а угол, то следует сначала найти сторону, проведя высоту таким образом, чтобы получить прямоугольный треугольник с заданным углом. Тогда сторона a может быть найдена из тригонометрических отношений по формуле  . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит
. Подставляя это выражение в ту же стандартную формулу площади ромба, выходит 
