Как найти площадь неровной фигуры 4 класс

Оборудование. Учебник Э.И.Александровой
(изд-во ВИТА-ПРЕСС), на каждого ученика листочки
четырёх цветов, листочки с четырьмя вариантами
заданий, непрозрачные конверты с палетками из
целлофана, два больших демонстрационных листа с
рисунками 2 и 3, 6 листов для работы (по количеству
групп) с фигурой на рисунке 2, 12 листов с фигурой
на рисунке 3.

Тема. Измерение площадей криволинейных
фигур. Палетка.

Цели.

Образовательная: познакомить с способом
измерения площадей криволинейных фигур; с
устройством для измерения площадей – палеткой;
закреплять умение находить площади
прямолинейных фигур.

Развивающая: развивать внимание,
наблюдательность, умение рассуждать, обобщать и
делать выводы.

Воспитательная: воспитывать умение общаться,
аккуратность, внимательность.

1. Учебная ситуация успеха

Учитель. Чем мы занимались на вчерашнем уроке?

Ученики. Находили площади и периметры фигур.

Учитель. Как найти площадь геометрической
фигуры?

Ученики. Площадь прямоугольника и треугольника
находят по формуле. Если это не прямоугольник и
не треугольник, то сначала многоугольник надо
разбить или достроить до фигур, площади которых
мы уже знаем как находить.

Учитель. Я предлагаю вам выполнить эти задания.
Здесь 4 варианта заданий. Посмотрите на них и
выберите себе любое. Все 4 варианта лежат у вас на
партах.

На доске четыре варианта заданий. Каждое
записано своим цветом. У детей на партах кроме
карточек с фигурами четырёх цветов, квадраты
соответствующих цветов.

На доске

Дети, решив задание, поднимают карточку с
соответствующим заданию цветом. По цвету они
находят группу, сверяют решение, выбирают одного
представителя от группы, который записывает
решение на доске. Остальные сверяют свои ответы с
доской.

Учитель. Ребята, научились мы находить площади
геометрических фигур?

Ученики. Да.

2. Постановка учебной задачи

Учитель. А теперь найдите площадь этой фигуры.

Показывает и вывешивает на доску

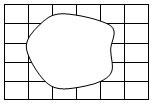
Ученики молчат.

Учитель. Почему вы не можете выполнить задание?

Ученики. Это не прямоугольник и не треугольник.
Это не многоугольник.

Учитель. Чем эта фигура отличаются от нам
известных фигур, многоугольников?

Ученики. Непонятно, где длина, ширина. Нет углов.
Фигуры некрасивые, какие-то кривые.

Учитель. Да, все многоугольники состоят из
прямых линий. Поэтому их называют прямолинейными
фигурами. А из каких линий состоят эти фигуры?

Как бы вы их назвали?

Ученики. Кривые.

Учитель. В математике такие фигуры называют криволинейными.

Учитель. Чем же мы будем заниматься сегодня на
уроке?

Ученики. Учиться находить площади
криволинейных фигур.

Учитель фиксирует проблему на доске:

S = ?

3. Поиск решения поставленной задачи

Учитель. Как же мы будем решать эту задачу? Как
вы находили площадь прямоугольника, когда ещё не
знали формулу его площади?

Ученики. Мы измеряли площадь прямоугольника с
помощью мерки.

Учитель. А для криволинейной фигуры такой
способ можно попробовать?

Ученики. Да.

Учитель. Как можно узнать площадь
криволинейной фигуры с помощью мерки в одну
клетку?

Ученики. Разбить на мерки, продолжив линии
клеток-мерок.

Учитель. Что будете делать, когда разобьёте
фигуру на мерки, чтобы узнать площадь фигуры?

Ученики. Посчитаем количество мерок в фигуре.

Учитель. Работаем в группах.

Представители от групп записывают свои ответы
на доске. Ответы оказываются разными.

Учитель. Почему ответы оказались разными? Наши
ребята не умеют считать?

Группа, у которой количество мерок меньше,
объясняют: “Мы не считали нецелые мерки”.

Учитель. Правильно будет вообще не считать
неполные мерки?

Ученики. Нет.

Учитель. А считать половинку как полную
мерку-квадрат можно?

Ученики. Нет.

Учитель. Что же делать с неполными мерками,
ребята? Как их считать?

Ученики. Складывать по две мерки.

Учитель. Да, в математике договорились считать
всё количество неполных мерок и делить на 2.

Учитель. Посчитайте ещё раз количество полных
мерок. Неполных мерок.

Ученики работают в группах.

Учитель. Скольким квадратным меркам равна
площадь фигуры?

Представители от групп называют ответы. Все
сверяют со своими ответами.

4. Моделирование

Учитель. Что мы сейчас нашли?

Ученики. Мы узнали площадь криволинейной
фигуры.

Учитель. Давайте вспомним, как мы это делали.

Дети говорят, учитель записывает на доске.

1. Разбить на мерки.

1. Посчитать полные мерки.

2. Посчитать неполные мерки и разделить на 2.

3. Сложить.

Учитель. Так можно найти площадь только этой
криволинейной фигуры?

Ученики. Можно найти площадь и другой фигуры.

Учитель. Как записать, чтобы было понятно, что
таким способом можно воспользоваться для
вычисления площади любой криволинейной фигуры?

Как обозначить полные мерки? Неполные мерки?

Дети предлагают разные варианты. Учитель
сообщает, что в математике договорились полные
мерки обозначать буквой n, а неполные мерки
буквой m.

Учитель. Кто закончит запись S_o = ?

На доске появляется запись: S_o = n + m : 2

Физминутка

5. Рефлексия

Учитель. Откройте учебники на стр. 61. Найдите №
88. Работая в парах, узнайте площади криволинейных
фигур: 1 ряд – площадь первой фигуры, 2 ряд –
площадь второй фигуры, 3 ряд – площадь третьей
фигуры.

Проверка

Представители от пар, выполнивших задание
первыми, записывают на доске ответы. Остальные
сравнивают свои ответы с их записями.

Учитель. По какой формуле вы находили площадь
криволинейной фигуры?

Ученики. S = n + m : 2

Учитель. При таком способе нахождения площади
(путём разбиения фигуры на мерки-квадраты)
измерения получаются неточными.

Какие единицы измерения площадей вы знаете?

Ученики. Кв.см, кв.мм, кв.м, кв.км.

Учитель. Откройте учебник на с. 62 , № 89.

Одну и ту же фигуру измеряли сначала в кв.см,
потом в кв. мм

Как вы думаете, в каком случае измерения
выполнены более точно: в кв. см или в кв.мм?

Ученики. Более точно измерили квадратными мм .

6. Конкретизация способа нахождения площади
криволинейной фигуры

Учитель. Мы научились измерять площади
криволинейных фигур, разбивая их на клетки –
мерки.

А сейчас посмотрите вот на эту фигуру:

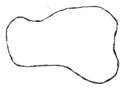
Надо узнать площадь этой фигуры с помощью мерки
в 1 кв. см.

Чем отличается данное задание от предыдущего?

Ученики. Нет клеточек, по которым можно
провести линии мерок.

Учитель. Да, здесь нет сетки из квадратов. Как же
узнать, сколько полных и неполных кв. см
поместилось в данной фигуре?

Все задумались и молчат. Один ученик предлагает
свою версию – накинуть сверху какую-нибудь сетку
из квадратиков.

Учитель. Да, можно изготовить специальное
устройство (показываю). Это палетка.

Достаньте из конверта палетку. Кто догадался,
как её сделали?

Ученики. Расчертили на квадраты со стороной в 1
см.

Учитель. А как ей пользоваться?

Ученики. Наложить на фигуру и посчитать
количество клеток.

Посчитайте в парах площадь этой криволинейной
фигуры.

Учитель. Выполните задание в учебнике №
90.Каждый самостоятельно.

Проверка.

Три первых ученика, выполнивших задание,
выходят к доске и записывают свои ответы

Класс сверяет ответы.

7. Дз.

Учитель. Дома вам надо найти площади фигур из №
91. Что вам для этого понадобится?

Ученики. Палетка.

Учитель. Кто сможет сделать её сам?

Как это сделать?

Думаю, что все справятся с этой работой.

Если вы увидите фигуру, площадь которой можно
найти другим способом, то вычислите площадь
такой фигуры двумя способами: с помощью палетки и
без неё.

8. Итоговая рефлексия

Учитель. Какую задачу решали на уроке?

Ученики. Учились находить площадь
криволинейной фигуры.

Учитель. Кто сможет дома рассказать родителям
,как найти площадь криволинейной фигуры?

Как это сделать?

Учитель. А как вы думаете, чем мы будем
заниматься на следующих уроках?

Ученики. Будем решать задачи на нахождение
площадей фигур.

Будем находить новые формулы для нахождения
площадей фигур.

Учитель. Да, на следующих уроках мы будем
использовать полученные знания в решении задач.

Математика, 4 класс

Урок №14. Измерение площади фигуры с помощью палетки

Перечень вопросов, рассматриваемых в теме:

Площадь геометрической фигуры.

Вычисление площади фигур произвольной формы, используя палетку.

Глоссарий по теме:

Площадь – свойство фигур занимать место на плоскости.

Длина – свойство предмета “быть протяжённым в пространстве”

Палетка – прозрачная пластинка, разделенная на единицы площади.

Основная и дополнительная литература по теме урока:

1. Математика: 4 класс: учебник в 2 ч. Ч.1/ М.И.Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова, С.В.Степанова – М. Просвещение, 2016. – с. 36-38
2. Всероссийские проверочные работе. Математика. Рабочая тетрадь 4 класс в 2 ч. Ч 1/ под.ред. Н.А. Сопруновой – М.; Просвещение, 2016. – с. 50 -68

Теоретический материал для самостоятельного изучения

Вычислите площадь прямоугольника, если известно, что его длина равна 8см, а ширина 5см.

Вы уже знаете, чтобы найти площадь прямоугольника, нужно длину умножить на ширину. S= 8 ∙ 5 = 40 см²

А теперь попробуйте вычислить площадь данной фигуры:

-?

Сегодня мы узнаем, что для нахождения площади фигур можно использовать палетку. Палетка – это прозрачная плёнка, которая может быть разбита на квадратные дециметры, квадратные сантиметры, квадратные миллиметры. Простейшая палетка – лист кальки, разделенный на квадратные сантиметры. Палетку используют для измерения площади фигур, ограниченных кривой линией.

Чтобы найти площадь данной фигуры, нужно:

1) На данную фигуру наложить палетку. Не сдвигать!

2)Сосчитать, сколько целых клеток- квадратных единиц – содержится в фигуре.

Целых 34 клетки.

3) Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.

Неполных 8 клеток.

4) Количество нецелых квадратных единиц разделить на 2, примерно столько целых квадратных единиц они образуют.

8 : 2 = 4

5) Сложить числа, полученные в пунктах 2 и 4.

6) В ответе записать, что площадь фигуры приблизительно равна найденной сумме.

S = 34 + (8 : 2) = 38 см²

Ответ: S = 38 см²

Задания тренировочного модуля:

1. Определите, какая фигура имеет большую площадь, а какая – меньшую, и решите ребус соответствия.

Правильный ответ: Прямоугольник – большую, круг – меньшую.

Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.

Правильный ответ:

Площадь 7 см²

Периметр 12 см

На этой странице вы найдете ответ на вопрос Как найти площадь неровной фигуры?. Вопрос
соответствует категории Математика и уровню подготовки учащихся 1 – 4 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S
_ABC = S_ABCD : 2

S
_ABC = 20 : 2 = 10 см²

S
_ABC =
S
_ACD = 10 см²

---

Ваши комментарии

Оставить комментарий:

---