Как найти площадь незакрашенной фигуры квадрата

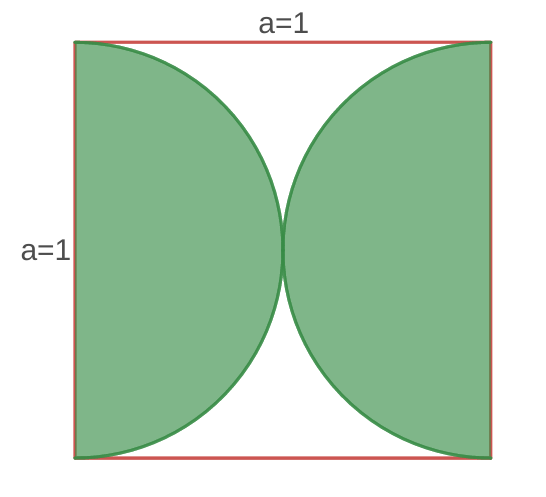
Если соединить середины сторон квадрата, получим квадрат с диагональю 4. Внутри него окажутся восемь закрашенных сегментов кругов, которые по площади равны восьми незакрашенным сегментам кругов, расположенных вдоль диагоналей квадрата со стороной 4 (грубо говоря, в его углах).

Таким образом, площадь незакрашенной части квадрата 4х4 будет равна площади квадрата с диагональю 4 или 4²/2 = 8.

Но можно и побольше заморочиться. Площадь квадрата равна 4² = 16. Диаметр полукругов равен 4/2 = 2, значит, радиус равен 1, а площадь каждого из них π/2. Площадь восьми полукругов – 4π. Но полукруги пересекаются, поэтому из этой площади необходимо исключить площадь восьми секторов (они как раз не закрашены), равную 8*(π/4 – 1/2) = 2π – 4. Т.о. площадь, занятая полукругами, равна (4π – 2π + 4) = 2π + 4. Площадь незакр. части квадрата будет равна разнице площади квадрата и площади, занятой полукругами, плюс площадь восьми незакрашенных секторов.

16 – 2π – 4 + 2π – 4 = 8.

Получили тот же самый результат.

Ответ. Правильный вариант – (Б), площадь части квадрата, оставшейся незакрашенной, равна 8.

Есть много задач на нахождение площадей фигур, полученных в результате разнообразных пересечений и наложений многоугольников и окружностей. Такие задачи очень интересно решать, если включить воображение, мысленно достраивая исходные рисунки до полных фигур, применяя соображения симметрии, используя идеи поворота или проводя дополнительные построения.

Решение задач на площади полученные в результате разнообразных пересечений многоугольников и окружностей

Рассмотрим один пример такой задачи.

Задача 1

Найди площадь незакрашенной части квадрата.

“Разрежем” рисунок на две одинаковые части вертикальной осью симметрии и переставим их. Получим квадрат и вписанный в него зеленый круг.

Тогда площадь незакрашенной части квадрата равна площадь квадрата минус площадь круга с радиусом 0.5.

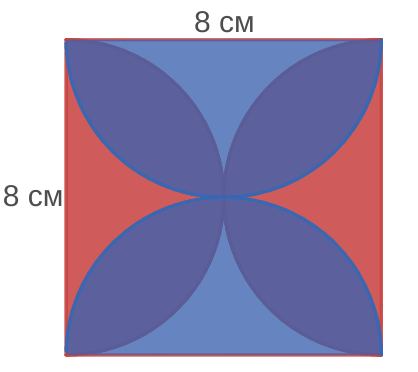
 Задача 2

Еще один пример:

Найди площадь закрашенной фиолетовым цветом фигуры См. исходный рис. слева).

 

Как можно быстро решить такую задачу?

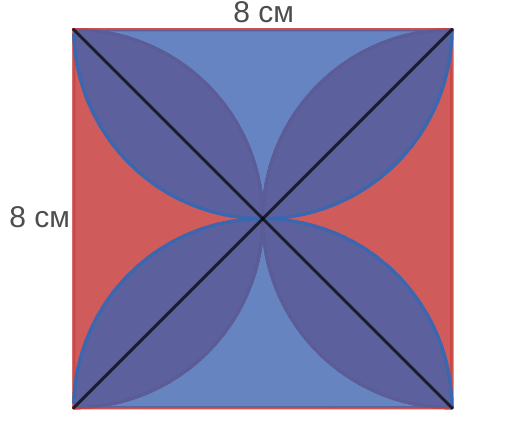
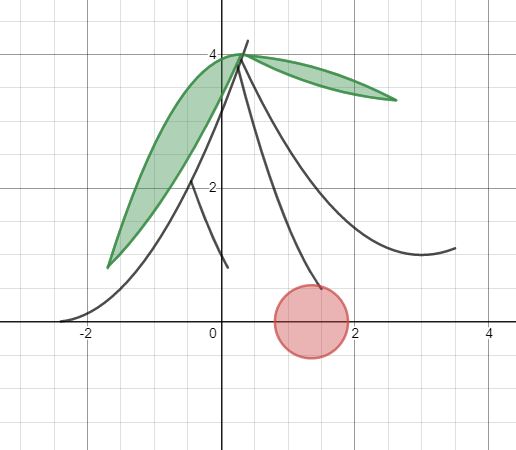
1. Проведем диагонали исходного квадрата, получим второй рис. 
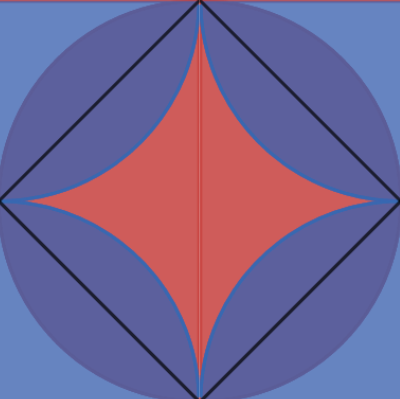
2. “Разрежем” его на две одинаковые части вертикальной осью симметрии и переставим их. Работать будем с третьим рисунком.
3. Из площади получившегося после преобразования картинки круга (с радиусом 4), вписанного в большой квадрат,  вычтем площадь малого квадрата (он обведен на 3-м рисунке черным).
4. Полученную площадь удвоим.
5. Искомая площадь равна примерно 36,5 кв. см. Точнее площадь даст формула.

Коллекция Фигуры и формы

 Такие вот вызовы можно найти на Pinterest

Формы и фигуры с помощью аналитических записей

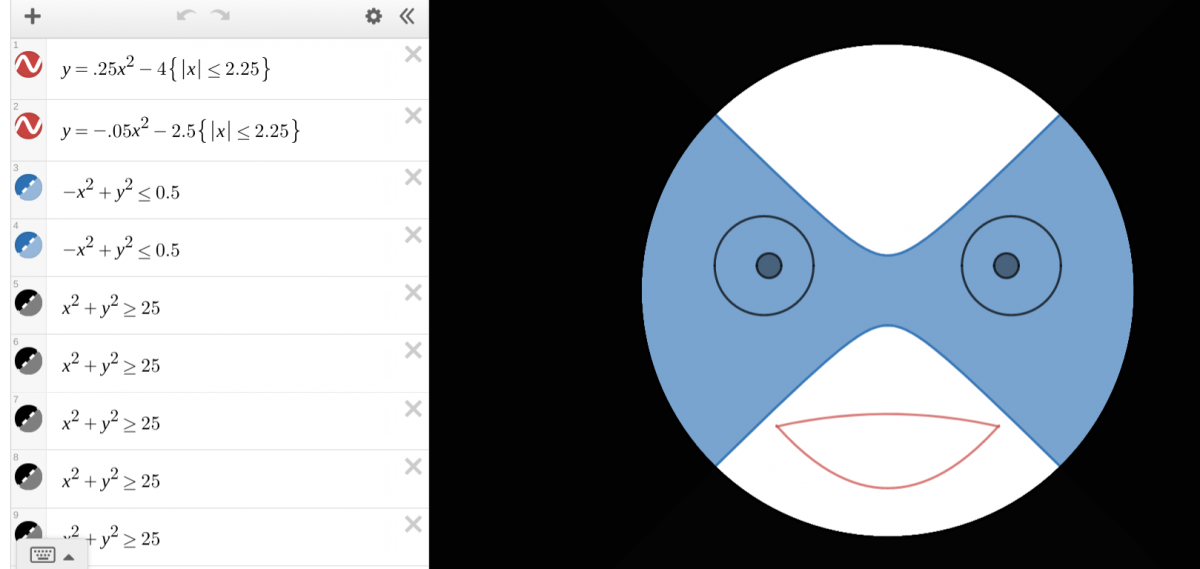
Отдельная задача – “нарисовать” такие чертежи с помощью аналитических записей в Desmos.

Такой рисунок в качестве заставки к активности создал с помощью функций и неравенств ученик 11 класса TKVG Валерий Чернов.

Использованы уравнение и неравенство окружности, квадратичные функции, заданные на отрезке, неравенства с модулем.

Вообще тема “рисования” окружностями и кругами очень интересна для освоение учениками именно с использованием Desmos.

Впервые уравнение окружности для необычных задач мной было использовано в этой статье!

Уроки в Desmos продолжаются… Повесь ягоду на ветку!

Вот тот самый апплет

Добавь на ветки ягоды! 

Упражнения на уравнение и неравенство окружности: круг и полукруг

Круг и полукруг

Фигура 5

Рассмотрим еще несколько задач на создание таких во рисунков с использованием в аналитических записях уравнения окружности…

Фигура 1

Фигура 2

Фигура 3

Квадрат создается с помощью знакомых уже таблиц и полигонов

Чтобы внутри квадрата “нарисовать” два полукруга, зададим их с помощью записей: неравенства окружности и неравенства для обозначения области его задания

Для “прорисовки” кругового сектора начнем с создания угла, сделаем это при помощи двух отрезков

Для того, чтобы “нарисовать” сектор и “закрасить” его черным, прибегнем к записям неравенствами

Еще одна задача: требуется создать довольно сложную картинку, состоящую из нескольких закрашенных разными цветами областей. Начнем с закрашенного квадрата (полигон), сложного цвета добиваемся последовательным “наложением” цветов: красного и синего.

Пересечение двух полукругов даст требуемый фиолетовый цвет.

Продолжение следует…

Обновление на 25.11.19

Продолжаются уроки математики с использованием активностей в TeacherDesmos, разработанных учениками нашей гимназии.
В 8б прошел урок математики по сценарию, предложенному Валерием Черновым, учеником G2.2.

Предложенные задания, вызвали интерес у ребят. В течение урока они обсуждали и предлагали разные варианты решения задач.
Сегодня этот же урок был проведен в том же классе, где учится сам Валерий, естественно, он был главным экспертом по этой теме.

Публикации по теме

• Идеи заданий с подвижными отрезками
• Виртуальный геоборд своими руками
• От бумаги к цифре: утренние ремиксы
• Мондриан как артефакт
• Ремикс-проект начинается с рамы
• Клетчатая Ёлка и новогодние ремиксы
• Математическая задача как вызов. Уроки в Desmos
• Инструкция: как создать “объект в зеркале” в среде Desmos
• Курс Desmos-математики стартовал!
• Математики больше не плачут, они анализируют проблемы
• Polygon: от подвижных геометрических фигур до картин
• Страсть к кругам и окружностям
• Задачи на оптимизацию — с помощью ползунков Desmos
• Списки? А для чего они нужны? Потренируемся?
• О “Розе ветров” и других визуализациях-ремиксах в Desmos
• По следам курса Desmos-математики: бери и делай!

Задача из Рабочей тетради по математике, 4 класс, часть2, Автор – Дорофеев, пр. Перспектива

Определи площади закрашенной и незакрашенной частей данного квадрата.

Решение: Чтобы определять площади этих треугольничков, нужно дорисовывать их до прямоугольников и находить площади этих прямоугольников (длину одной стороны умножить на длину другой), а потом делить на два.

Получается:

• площадь закрашенной части: 34 клетки
• площадь незакрашенной части: 30 клеток
• площадь закрашенной части больше, чем незакрашенной

См. ответ:

См. еще :

Как разрезать треугольник на 3 тупоугольных треугольника (математика, 4 класс, Дорофеев)

Плитка шоколада раскололась на 5 кусков, как разделить ее между 3 детьми (математика, 4 класс, Дорофеев)

Приложения:

---