A combined figure is a geometrical shape that is the combination of many simple geometrical shapes.
To find the area of combined figures we will follow the steps:
Step I: First we divide the combined figure into its simple geometrical shapes.
Step II: Then calculate the area of these simple geometrical shapes separately,
Step III: Finally, to find the required area of the combined figure we need to add or subtract these areas.
Solved Examples on Area of combined figures:
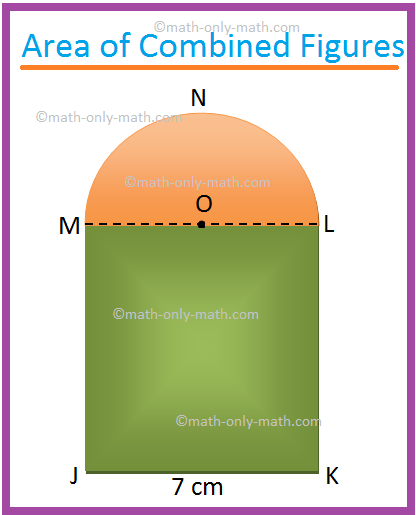
1. Find the area of the shaded region of the adjoining figure. (Use π = (frac{22}{7}))
JKLM is a square of side 7 cm. O is the centre of the
semicircle MNL.
Solution:
Step I: First we divide the combined figure into
its simple geometrical shapes.
The given combined shape is combination of a
square and a semicircle.
Step II: Then calculate the area of
these simple geometrical shapes separately.
Area of the square JKLM = 72 cm2
=
49 cm2
Area of the semicircle LNM = (frac{1}{2}) π ∙ ((frac{7}{2})^{2}) cm2 , [Since,
diameter LM = 7 cm]
=
(frac{1}{2}) ∙ (frac{22}{7}) ∙ (frac{49}{4}) cm2
=
(frac{77}{4}) cm2
=
19.25 cm2
Step III: Finally, add these areas up to get
the total area of the combined figure.
Therefore, the required area = 49 cm2 + 19.25 cm2
=
68.25 cm2.
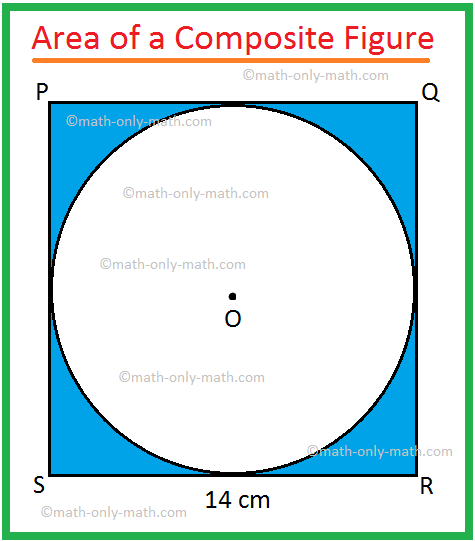
2. In the adjoining figure, PQRS is a square of side 14 cm
and O is the centre of the circle touching all sides of the square.
Find the area of the shaded region.
Solution:
Step I: First we divide the combined figure into its simple geometrical shapes.
The given combined shape is combination of a square and a circle.
Step II: Then calculate the area of these simple geometrical shapes separately.
Area of the square PQRS = 142 cm2
= 196 cm2
Area of the circle with centre O = π ∙ 72 cm2, [Since, diameter SR = 14 cm]
= (frac{22}{7}) ∙ 49 cm2
= 22 × 7 cm2
= 154 cm2
Step III: Finally, to find the required area of the combined figure we need to subtract the area of the circle from the area of the square.
Therefore, the required area = 196 cm2 – 154 cm2
= 42 cm2
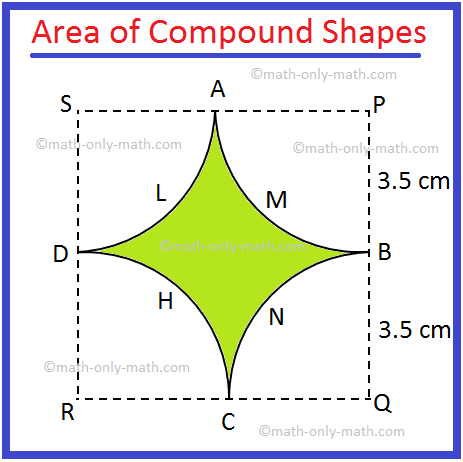
3. In the adjoining figure alongside, there are four equal quadrants of circles each of radius 3.5 cm, their centres being P, Q, R and S.
Find the area of the shaded region.
Solution:
Step I: First we divide the combined figure into its simple geometrical shapes.
The given combined shape is combination of a square and four quadrants.
Step II:Then calculate the area of these simple geometrical shapes separately.
Area of the square PQRS = 72 cm2, [Since, side of the square = 7 cm]
= 49 cm2
Area of the quadrant APB = (frac{1}{4}) π ∙ r2 cm2
= (frac{1}{4}) ∙ (frac{22}{7}) ∙ ((frac{7}{2})^{2}) cm2, [Since, side of the square = 7 cm and radius of the quadrant = (frac{7}{2}) cm]
= (frac{77}{8}) cm2
There are four quadrants and they have the same area.
So, total area of the four quadrants = 4 × (frac{77}{8}) cm2
= (frac{77}{2}) cm2
= (frac{77}{2}) cm2
Step III: Finally, to find the required area of the combined figure we need to subtract the area of the four quadrants from the area of the square.
Therefore, the required area = 49 cm2 – (frac{77}{2}) cm2
= (frac{21}{2}) cm2
= 10.5 cm2
10th Grade Math
From Areas of Combined Figures to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Площадь фигуры — это аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Содержание:
- Понятие площади
- Площади прямоугольника и прямоугольного треугольника
- Площади треугольников
- Площади четырехугольников и многоугольников
Понятие площади
Площадь — это тоже величина. Каждой плоской геометрической фигуре соответствует своя площадь. У пространственных фигур тоже есть соответствующая им площадь, называемая площадью поверхности.
Площадь фигур мы будем обозначать буквой S. Запись 
читается как «площадь фигуры F».
Определение. Измерить площадь фигуры — это значит сравнить ее с площадью некоторой фигуры, принятой за единицу измерения площади.
Измерить площадь фигуры в Древней Греции означало построить квадрат, площадь которого равна площади данной фигуры. С тех пор всякое вычисление площади принято называть квадратурой.
Если за единицу длины принимается 1 мм, то единицей площади является 1 
(квадратный миллиметр); при единице длины 1 см единицей площади является 1 
(квадратный сантиметр). Если единицей измерения длины является 1 м, ему соответствует единица площади 1
(квадратный метр).
Любую площадь S можно выразить через единицу измерения площади в виде 
, где k — числовой множитель, который показывает, сколько раз единичный квадрат укладывается в данной фигуре.
Пусть, например, за единицу измерения площади принят квадратный сантиметр (т. е. 
). Тогда запись 
означает, что площадь фигуры равна 
, т. е. в данной фигуре квадрат со стороной 1 см укладывается 15 раз.
Можно сфорулировать свойства измерения площади.
1. Всякий многоугольник F имеет площадь 
. Площадь является величиной, численное значение которой неотрицательно, т. е. 
для любой фигуры F.
Площадь фигуры зависит только от ее размеров и формы и не зависит от места расположения фигуры в пространстве. Это формулируется так.
2. Если две фигуры равны, то равны и их площади.
Пусть дана фигура F, которая является объединением двух фигур 
, причем эти фигуры пересекаются не более чем по конечному числу отрезков и точек. Тогда
Есть случаи, когда фигура является объединением двух других фигур, но данное равенство не выполняется. На рисунке 2.138 изображены два треугольника 
Фигура R — их объединение. В этом случае 
(при сложении площадь ромбовидной области в центре рисунка войдет в сумму дважды).
Еще одно свойство площади формулируется следующим образом.
3. За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения длины отрезка.
Для фигуры, разбитой на части, справедливо следующее свойство.
4. Если фигура разбита на части, то площадь фигуры равна сумме площадей частей фигуры.
Свойство измерения площади квадрата.
5. Площадь квадрата со стороной 
равна 
.
В геометрии различают фигуры равные и равновеликие.
Определение. Две фигуры называются равновеликими, если они имеют одинаковую площадь.
Площади прямоугольника и прямоугольного треугольника
Теорема 33. Площадь прямоугольника равна произведению его основания на высоту.
где 
— стороны прямоугольника.
Проведя диагональ АС прямоугольника ABCD (рис. 2.139), можно легко доказать, что она разбивает этот прямоугольник на два равных треугольника ABC и CDA, а тогда нетрудно доказать теорему 34.
Теорема 34. Площадь прямоугольного треугольника равна половине произведения его катетов (рис. 2.140):
где — катеты прямоугольного треугольника.
Площади треугольников
Теорема 35. Площадь треугольника равна половине произведения основания и высоты.
На рисунке 2.141 изображен треугольник ABC.
Есть еще одна формула для вычисления площади треугольника через его стороны. Эта формула носит имя древнегреческого математика Герона Александрийского (около I в.). Кроме этой формулы, есть еще так называемые ге-роновы треугольники — это треугольники, у которых целочисленные стороны и их площадь тоже есть целое число (примерами таких треугольников могут быть треугольники со сторонами 13, 14, 15 или 51, 52, 53).
Теорема 36 (формула Герона). Площадь треугольника равна
где 
— стороны треугольника, а р — его полупериметр, 
.
Существует формула площади треугольника, которая использует понятие синуса угла.
Теорема 37. Площадь треугольника равна половине произведения его сторон на синус угла между ними
где 
— стороны ААВС, а 
— угол между этими сторонами.
Площади четырехугольников и многоугольников
Для вывода формулы площади параллелограмма определим высоту параллелограмма.
Определение. Высотой параллелограмма называют отрезок перпендикуляра, проведенного из любой точки какой-нибудь стороны параллелограмма к прямой, содержащей противоположную сторону.
Высотой параллелограмма можно считать также и длину этого перпендикуляра. У параллелограмма две пары противоположных параллельных сторон и соответственно две высоты.
На рисунке 2.142 изображен параллелограмм ABCD, 
— его высоты. Заметим, что основания высот параллелограмма могут попасть и на продолжение одной из сторон (рис. 2.143).
Теорема 38. Площадь параллелограмма равна произведению его стороны и проведенной к ней высоты.
ABCD — параллелограмм, AD = ВС = 
, AM = CN = h (рис. 2.144).
Для вывода формулы площади еще одного четырехугольника — трапеции определяется понятие высоты трапеции.
Определение. Высотой трапеции называют отрезок перпендикуляра, проведенного из какой-либо точки основания трапеции к прямой, содержащей другое основание.
Высотой можно также считать длину этого перпендикуляра. На рисунке 2.145 ВМ — высота трапеции ABCD.
Теорема 39. Площадь трапеции равна произведению полусуммы оснований и высоты, т. е. если 
и 
— основания трапеции, h — высота и S — площадь трапеции, то
Чтобы вычислить площадь произвольного многоугольника, можно разбить его на треугольники, не имеющие общих внутренних точек, и найти сумму их площадей.
Такое разбиение выпуклого многоугольника можно осуществить, проведя, например, диагонали из одной его вершины (рис. 2.146). Иногда удобно пользоваться другими разбиениями (рис. 2.147, 2.148).
Пример:
Через середину основания треугольника проведены прямые, параллельные боковым сторонам. Докажите, что полученный таким образом четырехугольник — параллелограмм и что его площадь равна половине площади треугольника.
Решение:
Из условия задачи имеем:
1. 
2. AD = DC. (рис. 2.149)
3. DE || ВС, DF || АВ.
4. Надо доказать, что BEDF — параллелограмм и что 
5. Так как DE || ВС и DF || АВ, то BEDF — параллелограмм (2, определение параллелограмма).
Нужно установить связь между площадью параллелограмма и треугольника. Для этого удобно параллелограмм разбить на треугольники.
6. Соединим точки В и D и рассмотрим полученные треугольники (построение) (рис. 2.150).
7. 
равны (BD — общая сторона, 
и 
, как углы внутренние накрест лежащие при параллельных прямых (1, 2, 3, признак равенства треугольников по сторонам и двум прилежащим углам).
8. Эти треугольники и равновелики.
9. Треугольники BFD и CFD также равновелики между собой (хотя в общем случае они не равны), так как BF = FC (DF — средняя линия), т. е. основания их равны и они имеют одинаковую высоту, так как вершина D у них общая.
10. Аналогично равновелики между собой и 
11. 
следовательно, площади 
и параллелограмма BEDF можно записать так: 
а 
(8, 10, свойства площадей).
12. 
(11).
Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету “Математика”:
Лекции:
- Производные высших порядков. Формула Тейлора
- Статистические показатели
- Векторный анализ
- Система тригонометрических уравнений
- Формула дисперсии
- Системы дифференциальных уравнений. Методы интегрирования.
- Дифференциальные уравнения высших порядков
- Параллельность плоскостей
- Частные производные первого порядка
- Найти сходимость ряда
Приложения определенного интеграла
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Вычисление площади плоской фигуры.
Начать изучение
-
Плоская фигура и ее площадь.
Начать изучение
-
Площадь криволинейной трапеции.
Начать изучение
-
Площадь криволинейного сектора.
Начать изучение
-
Вычисление объема тела.
Начать изучение
-
Тело и его объем.
Начать изучение
-
Цилиндрическое тело и его объем.
Начать изучение
-
Объем тела вращения.
Начать изучение
-
Объем тела с заданными площадями поперечных сечений.
Начать изучение
-
Вычисление длины дуги кривой.
Начать изучение
-
Вычисление площади поверхности вращения.
Начать изучение
-
Применение определенного интеграла при решении физических задач.
Начать изучение
Вычисление площади плоской фигуры.
Плоская фигура и ее площадь.
Произвольное ограниченное множество точек плоскости будем называть плоской фигурой. Если плоскую фигуру можно представить как объединение конечного числа непересекающихся прямоугольников, то такую фигуру назовем клеточной. Подпрямоугольником будем понимать множество точек вида
$$
K = {(x, y): a_{1} leq x leq b_{1}, a_{2} leq y leq b_{2}}nonumber
$$
или множество, получаемое из (K) удалением части границы (или всей границы) множества (K).
Площадью прямоугольника (K) назовем число ((b_{1}-a_{1})(b_{2}-a_{2})) независимо от того, принадлежат или не принадлежат множеству (K) его граничные точки, а площадью клеточной фигуры назовем сумму площадей прямоугольников, из которых составлена эта фигура.
Замечание 1.
Можно показать, что площадь клеточной фигуры не зависит от способа разбиения ее на прямоугольники. Нетрудно также убедиться в том, что площадь клеточной фигуры неотрицательна и обладает свойствами:
- аддитивности, то есть площадь объединения двух непересекающихся клеточных фигур равна сумме их площадей;
- инвариантности, то есть площади двух равных (конгруэнтных) клеточных фигур совпадают;
- монотонности, то есть если клеточные фигуры (G_{1}) и (G_{2}) таковы, что (G_{1} subset G_{2}), то площадь фигуры (G_{1}) не превосходит площади фигуры (G_{2}).
Плоскую фигуру (G) назовем квадрируемой, если для любого (varepsilon > 0) найдутся клеточные фигуры (q) и (Q) такие, что
$$
q subset G subset Q,label{ref1}
$$
$$
0 leq S(Q)-S(q) < varepsilon,label{ref2}
$$
где (S(Q), S(q)) — площади фигур (Q) и (q) соответственно.
Пусть плоская фигура (G) квадрируема. Тогда площадью этой фигуры назовем число (S(G)) такое, что
$$
S(q) leq S(G) leq S(Q)label{ref3}
$$
для любых клеточных фигур (q) и (Q), удовлетворяющих условию eqref{ref1}.
Теорема 1.
Для любой квадрируемой фигуры (G) число (S(G)) существует и единственно, причем
$$
S(G) = sup S(q) = inf S(Q).label{ref4}
$$
Доказательство.
(circ) Так как для любых клеточных фигур (q) и (Q), удовлетворяющих условию eqref{ref1}, выполняется неравенство
$$
S(q) leq S(Q),nonumber
$$
то по теореме об отделимости существуют (sup S(q)) и (inf S(Q)) (супремум и инфимум берутся по всем клеточным фигурам, соответственно содержащимся в фигуре (G) и содержащим эту фигуру), причем
$$
S(q) leq sup S(q) leq inf S(Q) leq S(Q),label{ref5}
$$
откуда
$$
S(q) leq sup S(q) leq S(Q),label{ref6}
$$
Таким образом, число (S(G) = sup S(q)) удовлетворяет условию eqref{ref3}.
Докажем единственность числа (S(G)). Предположим, что наряду с числом (S(G)) существует еще одно число (S'(G)), удовлетворяющее условию eqref{ref3}, то есть
$$
S(q) leq S^{‘}(G) leq S(Q),label{ref7}
$$
Тогда из eqref{ref3} и eqref{ref7} в силу свойств неравенств получаем, что
$$
|S(G)-S'(G)| leq S(Q)-S(q)label{ref8}
$$
для любых клеточных фигур таких, что (q subset G subset Q). Так как (G) -квадрируемая фигура, то разность (S(Q)-S(q)) можно сделать сколь угодно малой в силу условия eqref{ref2}, выбрав соответствующие фигуры (Q) и (q). Поэтому из eqref{ref8} следует, что (S'(G) = S(G)). Таким образом, квадрируемая фигура (G) имеет площадь (S(G)), причем в силу eqref{ref5} справедливо равенство eqref{ref4}. (bullet)
Теорема 2.
Для того чтобы плоская фигура (G) была квадрируема, необходимо и достаточно, чтобы для любого (varepsilon > 0) существовали такие квадрируемые плоские фигуры (tilde{q}) и (tilde{Q}), что
$$
tilde{q} subset G subset tilde{Q},quad 0 leq S(tilde{Q})-S(tilde{q}) < varepsilon,label{ref9}
$$
где (S(tilde{Q})) и (S(tilde{q})) — площади фигур (Q) и (q) соответственно.
Доказательство.
(circ) Необходимость условий eqref{ref9} очевидна, так как по определению квадрируемой фигуры эти условия выполняются, если взять (tilde{q} = q, tilde{Q} = Q), где (q) и (Q) — клеточные фигуры, удовлетворяющие соотношениям eqref{ref1}, eqref{ref2}.
Докажем достаточность. Фиксируя произвольное число (varepsilon > 0), найдем в силу eqref{ref9} такие квадрируемые плоские фигуры (tilde{q}) и (tilde{Q}), что
$$
tilde{q} subset G subset tilde{Q}, 0 leq S(tilde{Q})-S(tilde{q}) < frac{varepsilon}{2},label{ref10}
$$
Так как (tilde{q}) и (tilde{Q}) — квадрируемые плоские фигуры, то существуют клеточные фигуры (Q’) и (q’) такие, что
$$
q’ subset tilde{q},quad tilde{Q} subset Q’,quad 0 leq S(tilde{q})-S(q’) < frac{varepsilon}{4},quad S(Q’)-S(tilde{Q}) < frac{varepsilon}{4}.label{ref11}
$$
Из eqref{ref10} и eqref{ref11} следует, что
$$
q’ subset G subset Q’,quad 0 leq S(Q’)-S(q’) < varepsilon.nonumber
$$
Это означает, что (G) — квадрируемая фигура, причем
$$
S(G) = sup S(tilde{q}) = inf S(tilde{Q}). bulletnonumber
$$
Замечание 2.
Можно доказать, что площадь квадрируемой фигуры обладает свойствами аддитивности, инвариантности и монотонности (см. замечание 1).
Площадь криволинейной трапеции.
Одной из основных задач, приводящих к понятию определенного интеграла, является задача о площади криволинейной трапеции, то есть фигуры (G), задаваемой на плоскости (Oxy) условиями
$$
G = {(x, y): a leq x leq b, 0 leq y leq f(x)},label{ref12}
$$
где (f(x)) — функция, непрерывная на отрезке ([a, b]).
Утверждение 1.
Криволинейная трапеция (G) — квадрируемая фигура, площадь которой (S = S(G)) выражается формулой
$$
S = intlimits_a^b f(x) dx,label{ref13}
$$
Доказательство.
(circ) Пусть (T = {x_{i}, i = overline{0, n}}) — разбиение отрезка ([a, b]), (M_{i}) и (m_{i}) — соответственно наибольшее и наименьшее значения функции (f) на отрезке (Delta_{i} = [x_{i-1}, x_{i}], Delta x_{i} = x_{i}-x_{i-1}, i = overline{1, n}) (рисунок ниже).
Рассмотрим клеточную фигуру (q), составленную из прямоугольников (q_{i} (i = overline{1, n})), таких, что длина основания (i)-го прямоугольника равна (Delta x_{i}), а высота равна (m_{i}).
Аналогично определяется клеточная фигура (Q), составленная из фигур (Q_{i}), где (Q_{i}) — прямоугольник, длина основания которого (Delta x_{i}), а высота (M_{i}, i = overline{1, n}).
Очевидно, (q subset G subset Q), площади фигур (q) и (Q) соответственно равны
$$
S(q) = sum_{i=1}^{n}m_{i}Delta x_{i},quad S(Q) = sum_{i=1}^{n}M_{i}Delta x_{i}.nonumber
$$
Заметим, что
$$
S(q) = s_{T}, S(Q) = S_{T},label{ref14}
$$
где (s_{T}) и (S_{T}) — соответственно нижняя и верхняя суммы Дарбу для функции (f) при разбиении (T) отрезка ([a, b]).
Так как функция (f(x)) непрерывна на отрезке ([a, b]), то в силу критерия интегрируемости для любого (varepsilon > 0) найдется такое разбиение (T) этого отрезка, что
$$
0 leq S_{T}-s_{T} < varepsilon.nonumber
$$
Иными словами (см. равенства eqref{ref14}), существуют клеточные фигуры (q) и (Q) такие, что
$$
q subset G subset Q,quad 0 leq S(Q)-S(q) < varepsilon,nonumber
$$
то есть выполняются условия eqref{ref1}, eqref{ref2}. Это означает, что (G) — квадрируемая фигура и согласно теореме 1 справедливо равенство eqref{ref4}, которое в силу равенств eqref{ref14} можно записать в виде
$$
S(G) = sup s_{T} = inf S_{T}.label{ref15}
$$
Используя следствие из критерия интегрируемости функции, получаем
$$
sup s_{T} = inf S_{T} = intlimits_a^b f(x) dx.label{ref16}
$$
Из eqref{ref15} и eqref{ref16} следует, что площадь (S = S(G)) криволинейной трапеции (G) выражается формулой eqref{ref13}. (bullet)
Замечание 3.
Ранее площадь (S) фигуры (G) была определена как предел интегральной суммы (sigma_{T} = displaystylesum_{i=1}^{n}f(xi_{i})Delta x_{i}) при (l(T) rightarrow 0) при условии, что этот предел не зависит от разбиения (T) и выборки (xi = {xi_{i}, i = overline{1, n}}), где (xi_{i} in Delta_{i}). Для непрерывной на отрезке ([a, b]) функции (displaystylelim_{l(T) longrightarrow 0}sigma_{T}(xi) = intlimits_a^b f(x) dx), и поэтому оба определения площади приводят к одному и тому же результату.
Рассмотрим теперь фигуру (D) (рис. 37.1), ограниченную отрезками прямых (x = a) и (x = b) и графиками непрерывных на отрезке ([a, b]) функций (y = f_{1}(x)) и (y = f_{2}(x)), где (f_{1}(x) leq f_{2}(x)) при (x in [a, b]). Если (f_{1}(x) geq 0) для всех (x in [a, b]), то площадь фигуры (D) равна разности площадей криволинейных трапеций (D_{2}) и (D_{1}), где (D_{i} = {(x, y): a leq x leq b, 0 leq y leq f_{i}(x)}, i = 1,2). Поэтому площадь фигуры (D) выражается формулой
$$
S(D) = intlimits_a^b (f_{2}(x)-f_{1}(x)) dx.label{ref17}
$$
Формула eqref{ref17} остается в силе и в случае, когда не выполняется условие (f_{1}(x) geq 0) для всех (x in [a, b]). Чтобы убедиться в этом, достаточно сдвинуть фигуру (D) вдоль положительного направления оси (Oy) на (y_{0} = displaystylevertmin_{x in [a, b]}f_{1}(x)vert) и воспользоваться тем, что площади равных фигур совпадают.
Пример 1.
Найти площадь (S) фигуры, ограниченной эллипсом
$$
frac{x^{2}}{a^{2}} + frac{y^{2}}{b^{2}} = 1nonumber
$$
Решение.
(triangle) Искомая площадь (S) равна (4sigma), где (sigma) (рис. 37.2) — площадь криволинейной трапеции, ограниченной осями (Ox), (Oy) и графиком функции (y = b displaystylesqrt{1-frac{x^{2}}{a^{2}}}, 0 leq x leq a). По формуле eqref{ref13} находим
$$
sigma = b intlimits_0^a sqrt{1-frac{x^{2}}{a^{2}}} dx = ab intlimits_0^1 sqrt{1-t^{2}} dt = frac{1}{4} pi abnonumber
$$
(см. пример здесь). Итак, площадь, ограниченная эллипсом с полуосями (a) и (b), равна
$$
S = pi abnonumber
$$
В частности, площадь круга радиуса (R) равна (pi R^{2}). (blacktriangle)
Отсюда следует, что площадь кругового сектора (радиуса (R)), соответствующего центральному углу (alpha), равна
$$
frac{pi R^{2}}{2pi}alpha = frac{R^{2}alpha}{2}.nonumber
$$
Пример 2.
Найти площадь фигуры, ограниченной параболой (y = 6x-x^{2}) и прямой (y = x + 4).
Решение.
(triangle) Парабола (y = 6x-x^{2}) пересекается с прямой (y = x + 4) в точках (A) и В (рис. 37.3), абсциссы которых являются корнями уравнения (6x-x^{2} = x + 4). Решая это уравнение, находим его корни (x_{1} = 1, x_{2} = 4). Согласно формуле eqref{ref17} искомая площадь (S) равна
$$
S = intlimits_1^4 ((6x-x^{2})-(x + 4)) dx = left(frac{5}{2}x^{2}-left.frac{x^{3}}{3}-4xright)right|_{1}^{4} = frac{9}{2}. blacktrianglenonumber
$$
Площадь криволинейного сектора.
Пусть кривая (Gamma) задана в полярной системе координат уравнением
$$
rho = rho(varphi),quad alpha leq varphi leq beta,nonumber
$$
где (rho(varphi)) — неотрицательная и непрерывная на отрезке ([alpha, beta]) функция. Тогда плоскую фигуру (G), ограниченную кривой (Gamma) и, быть может, отрезками двух лучей, составляющих с полярной осью углы (alpha) и (beta) (рис. 37.4), назовем криволинейным сектором.
Утверждение 2.
Криволинейный сектор (G) — квадрируемая фигура, площадь которой (S) выражается формулой
$$
S = frac{1}{2} intlimits_{alpha}^{beta} rho^{2}(varphi) dvarphi.label{ref18}
$$
Доказательство.
(circ) Пусть (T = {varphi_{i}, i = overline{0, n}}) — разбиение отрезка ([alpha, beta]), (m_{i}) и (M_{i}) — соответственно наименьшее и наибольшее значения функции (rho(varphi)) на отрезке (Delta_{i} = [varphi_{i-1}, varphi_{i}], i = overline{1, n}). Обозначим через (q_{i}) и (Q_{i}) круговые секторы, ограниченные лучами (varphi = varphi_{i-1}, varphi = varphi_{i}) и дугами окружностей радиусов (m_{i}) и (M_{i}) соответственно (рис. 37.4). Если (q) — объединение фигур (q_{1}, ldots, q_{n}), а (Q) — объединение фигур (Q_{1}, ldots, Q_{n}), то (q subset G subset Q).Так как (q_{i}) и (Q_{i}) — квадрируемые фигуры, то (q) и (Q) также являются квадрируемыми фигурами, а их площади соответственно равны
$$
S(q) = frac{1}{2} sum_{i=1}^{n}m_{i}^{2}Delta varphi_{i}quad mbox{и}quad S(Q) = frac{1}{2} sum_{i=1}^{n}M_{i}^{2}Delta varphi_{i}.nonumber
$$
Отсюда следует, что (S(q)) и (S(Q)) совпадают соответственно с нижней и верхней суммами Дарбу для функции (displaystylefrac{1}{2} rho^{2}(varphi)) на отрезке ([alpha, beta]). Поэтому (следствие из теоремы о критерии интегрируемости)
$$
sup S(q) = inf S(Q) = frac{1}{2} intlimits_{alpha}^{beta} rho^{2}(varphi) dvarphi.nonumber
$$
Это означает (теорема 2), что (G) — квадрируемая фигура, а ее площадь (S) выражается формулой eqref{ref18}. (bullet)
Пример 3.
Найти площадь фигуры (G), которая ограничена лемнискатой Бернулли (рис. 37.5), заданной уравнением
$$
rho^{2} = a^{2} cos 2varphi.nonumber
$$
Решение.
(triangle) Фигура (G) симметрична относительно координатных осей. Площадь (sigma) той части фигуры (G), которая лежит в первом квадранте, согласно формуле eqref{ref18} равна (sigma = displaystylefrac{1}{2} intlimits_0^{pi/4} a^{2} cos 2varphi dvarphi). Поэтому искомая площадь (S = 4sigma = a^{2}). (blacktriangle)
Вычисление объема тела.
Тело и его объем.
Произвольное ограниченное множество точек пространства будем называть телом.
Основные определения и утверждения, относящиеся к телам, аналогичны соответствующим определениям и утверждениям, рассмотренным выше. Поэтому некоторые утверждения для тел будут опущены.
По аналогии с понятием клеточной фигуры назовем тело клеточным, если его можно представить как объединение конечного числа непересекающихся параллелепипедов, то есть тел вида
$$
M = {(x, y, z): a_{1} leq x leq b_{1}, a_{2} leq y leq b_{2}, a_{3} leq z leq b_{3}},nonumber
$$
а также тел, получаемых из (M) удалением части границы (или всей границы) тела (M). Объемом параллелепипеда (M) назовем число ((b_{1}-a_{1})(b_{2}-a_{2})(b_{3}-a_{3})), а объемом клеточного тела — сумму объемов составляющих его параллелепипедов.
Тело (Omega) будем называть кубируемым, если для любого (varepsilon > 0) найдутся клеточные тела (p) и (P) такие, что
$$
p subset Omega subset P,quad 0 leq V(P)-V(p) < varepsilon,nonumber
$$
где (V(P)) и (V(p)) — объемы тел (P) и (p) соответственно. Как и в случае с площадью фигуры, легко показать, что если тело (Omega) кубируемо, то существует единственное число (V(Omega)) такое, что неравенство
$$
V(p) leq V(Omega) leq V(P)nonumber
$$
выполняется для любых клеточных тел (p), (P), удовлетворяющих условию (p subset Omega subset P); при этом
$$
V(Omega) = sup V(p) = inf V(P).nonumber
$$
Это число (V(Omega)) называют объемом тела (V). Рассмотрим некоторые классы кубируемых (имеющих объем) тел.
Цилиндрическое тело и его объем.
Пусть простой контур (Gamma), расположенный в плоскости (Oxy), ограничивает плоскую фигуру (G). Рассмотрим множество (Omega) точек пространства, которые получаются сдвигом фигуры (G) в направлении положительной полуоси (Oz) на расстояние, не превосходящее (h), где (h) — заданное число, и назовем (Omega) цилиндрическим телом. Граница этого тела состоит из равных (конгруэнтных) фигур (G) и (G_{1}) (рис. 37.6) и части цилиндрической поверхности, образующие которой параллельны оси (Oz). Фигуры (G) и (G_{1}) называют основаниями цилиндрического тела, а расстояние между плоскостями оснований — высотой этого тела.
Утверждение 3.
Если основанием цилиндрического тела (Omega) служит плоская квадрируемая фигура (G), то тело (Omega) кубируемо, а его объем (V(Omega)) равен (S(G)h), где (S(G)) — площадь основания, (h) — высота тела (Omega). В частности, объем прямого кругового цилиндра равен (V = pi R^{2}h), где (R) — радиус основания, (h) — высота цилиндра.
Доказательство.
(circ) По определению плоской квадрируемой фигуры для любого (varepsilon > 0) существуют такие клеточные фигуры (q) и (Q), что
$$
q subset G subset Q,quad 0 leq S(Q)-S(q) < frac{varepsilon}{h},nonumber
$$
Рассмотрим цилиндрические тела (Omega_{1}) и (Omega_{2}) основаниями которых служат соответственно фигуры (q) и (Q), а высота каждого из этих тел равна (h). Тела (Omega_{1}) и (Omega_{2}) являются клеточными, а их объемы соответственно равны
$$
V(Omega_{1}) = S(q)hquad mbox{и}quad V(Omega_{2}) = S(Q)h.nonumber
$$
Так как (Omega_{1} subset Omega subset Omega_{2}, 0 leq V(Omega_{2})-V(Omega_{1}) < varepsilon), то (Omega) — кубируемое тело, а его объем равен (S(G)h). (bullet)
Замечание 4.
Из свойства аддитивности объема и утверждения 3 следует, что ступенчатое тело, то есть тело, являющееся объединением конечного числа цилиндрических тел, кубируемо, если основания цилиндрических тел квадрируемы; при этом объем ступенчатого тела равен сумме объемов тел, из которых составлено ступенчатое тело.
Объем тела вращения.
Утверждение 4.
Тело, образованное вращением вокруг оси (Ox) криволинейной трапеции (G) (условие eqref{ref12}), где (f(x)) — функция, непрерывная на отрезке ([a, b]), кубируемо, а его объем (V) выражается формулой
$$
V = pi intlimits_a^b f^{2}(x) dx.label{ref19}
$$
Доказательство.
(circ) Пусть (T, m_{i}, M_{i}, Delta x_{i}, q, Q) — те же, что и в пункте про «площадь криволинейной трапеции». При вращении вокруг оси (Ox) фигур (q), (G), (Q) получаются тела вращения (p), (Omega), (P) такие, что
$$
p subset Omega subset P,nonumber
$$
причем объемы ступенчатых тел (p) и (P) соответственно равны
$$
V(p) = pi sum_{i=1}^{n}m_{i}^{2}Delta x_{i},quad V(P) = pi sum_{i=1}^{n}M_{i}^{2}Delta x_{i}.nonumber
$$
Так как (V(p)) и (V(P)) равны соответственно нижней и верхней суммам Дарбу для функции (pi f^{2}(x)) при разбиении (T) отрезка ([a, b]), то согласно следствию из теоремы о критерии интегрируемости
$$
sup V(p) = inf V(P) = pi intlimits_a^b f^{2}(x) dx.nonumber
$$
Следовательно, (Q) — кубируемое тело (по теореме, аналогичной теореме 2), а его объем выражается формулой eqref{ref19}. (bullet)
Пример 4.
Найти объем тела, полученного при вращении вокруг оси (Ox) фигуры, ограниченной осью (Ox) и графиком функции (y = sin x, 0 leq x leq pi).
Решение.
(triangle) По формуле eqref{ref19} получаем (V = pi displaystyleintlimits_0^{pi} sin^{2}(x) dx = frac{pi^{2}}{2}). (blacktriangle)
Объем тела с заданными площадями поперечных сечений.
Пусть тело (Omega) заключено между плоскостями, перпендикулярными оси Ох и пересекающими эту ось в точках (x = a) и (x = b), где (a < b) (рис. 37.7).
Обозначим через (G_{x}) фигуру, получаемую в сечении тела (Omega) плоскостью, перпендикулярной оси (Ox) и проходящей через точку (x in [a, b]) этой оси. Будем считать, что при любом (x in [a, b]) фигура (G_{x}) квадрируема, а ее площадь (sigma (x)) — функция, непрерывная на отрезке ([a, b]). Кроме того, предположим, что при проектировании на плоскость, перпендикулярную оси (Ox), фигур (G_{alpha}) и (G_{beta}), где (alpha, beta), — любые точки отрезка ([a, b]), получаются фигуры, одна из которых содержится в другой.
Утверждение 5.
При указанных выше условиях тело (Omega) кубируемо, а его объем (V) выражается формулой
$$
V = intlimits_a^b sigma(x) dx.label{ref20}
$$
Доказательство.
(circ) Пусть (T = {x_{i}, i = overline{0, n}}) — разбиение отрезка ([a, b]), (m_{i}) и (M_{i})-соответственно наименьшее и наибольшее значения функции (sigma(x)) на отрезке (Delta x_{i} = [x_{i-1}, x_{i}], Delta x_{i} = x_{i}-x_{i-1}, i = overline{1, n}). Так как (sigma(x)) — непрерывная функция, то существуют точки (xi_{i} in Delta_{i}) и (xi_{i}’) такие, что (sigma(xi_{i}) = m_{i}, sigma(xi_{i}’) = M_{i}, i = overline{1, n}).
Обозначим через (Omega_{i}) ту часть тела (Omega), которая заключена между плоскостями (A_{i-1}) и (A_{i}), перпендикулярными оси (Ox) и проходящими соответственно через точки (x_{i-1}) и (x_{i}) (см. рис. 37.7).
Пусть (D_{i}) и (D_{i}’) — цилиндрические тела высотой (Delta x_{i}), построенные на сечениях (G_{xi_{i}}) и (G_{xi_{i}’}) как на основаниях и расположенные между плоскостями (A_{i-1}) и (A_{i}). Тогда (D_{i} subset Omega_{i} subset D_{i}’) а объемы тел (D_{i}) и (D_{i}’) соответственно равны
$$
V(D_{i}) = m_{i}Delta x_{i},quad V(D_{i}’) = M_{i}Delta x_{i}.nonumber
$$
Если (p) — объединение тел (D_{1}, ldots, D_{n}), а (P) — объединение тел (D_{1}’, ldots, D_{n}’), то (p subset Omega subset P),
$$
V(p) = sum_{i=1}^{n}m_{i}Delta x_{i},quad V(P) = sum_{i=1}^{n}M_{i}Delta x_{i}.nonumber
$$
Так как (sup V(p) = inf V(P) = displaystyleintlimits_a^b sigma(x) dx), то (Omega) — кубируемое тело, a его объем выражается формулой eqref{ref20}. (bullet)
Пример 5.
Вычислить объем эллипсоида (displaystylefrac{x^{2}}{a^{2}} + frac{y^{2}}{b^{2}} + frac{z^{2}}{c^{2}} = 1).
Решение.
(triangle) Воспользуемся тем, что площадь фигуры (G), получаемой в сечении эллипсоида плоскостью, параллельной плоскости (Oyz) и отстоящей от нее на расстоянии (x_{0}), где (0 leq x_{0} leq a), равна
$$
S(x_{0}) = pi bc (1-frac{x_{0}^{2}}{a^{2}}).label{ref21}
$$
В самом деле, граница фигуры (G) — эллипс, задаваемый уравнениями
$$
frac{y^{2}}{b^{2}} + frac{z^{2}}{c^{2}} = 1-frac{x_{0}^{2}}{a^{2}},quad x = x_{0}
$$
Полуоси этого эллипса равны (blambda) и (clambda), где (lambda = displaystylesqrt{1-frac{x_{0}^{2}}{a^{2}}}). Используя пример 1, получаем формулу eqref{ref21}, а по формуле eqref{ref20} находим искомый объем эллипсоида:
$$
v = 2 intlimits_0^a S(x) dx = 2pi bc intlimits_0^a left(1-frac{x^{2}}{a^{2}}right) dx = frac{4}{3} pi abc.nonumber
$$
Отсюда следует, что объем шара, радиус которого равен (R), выражается формулой (v = displaystylefrac{4}{3} pi R^{3}) . (blacktriangle)
Вычисление длины дуги кривой.
Утверждение 6.
Если кривая (Gamma), заданная уравнением
$$
Gamma = {boldsymbol{r} = boldsymbol{r}(t), alpha leq t leq beta},label{ref22}
$$
непрерывно дифференцируема, то ее длина (S) выражается формулой
$$
S = intlimits_{alpha}^{beta} |boldsymbol{r}'(t)| dt.label{ref23}
$$
Доказательство.
(circ) Ранее было доказано, что непрерывно дифференцируемая кривая (Gamma) спрямляема (имеет длину), а производная переменной длины дуги (s(t)) этой кривой выражается формулой
$$
s'(t) dt = |boldsymbol{r}'(t)|.label{ref24}
$$
Пусть (S) — длина всей кривой (Gamma); тогда, используя равенство eqref{ref24} и формулу Ньютона-Лейбница, получаем
$$
intlimits_{alpha}^{beta} |boldsymbol{r}'(t)| dt = intlimits_{alpha}^{beta} s'(t) dt = s(beta)-s(alpha) = S.nonumber
$$
так как (s(beta) = S), a (s(alpha) = 0). (bullet)
Если (boldsymbol{r}(t) = (x(t), y(t), z(t))), то формула eqref{ref23} принимает вид
$$
S = intlimits_{alpha}^{beta} sqrt{(x'(t))^{2}+(y'(t))^{2}+(z'(t))^{2}} dt.label{ref25}
$$
а если (Gamma)-плоская кривая, заданная уравнением
$$
y = f(x),quad a leq x leq b,nonumber
$$
то ее длина выражается формулой
$$
S = intlimits_a^b sqrt{1 + (f^{‘}(x))^{2}} dx.label{ref26}
$$
Пример 6.
Найти длину кривой (y = operatorname{ch} x, 0 leq x leq a).
Решение.
(triangle) Применяя формулу eqref{ref26}, находим
$$
S = intlimits_0^a sqrt{1 + operatorname{sh}^{2}x} dx = intlimits_0^a operatorname{ch} x dx = operatorname{sh} a. blacktrianglenonumber
$$
Вычисление площади поверхности вращения.
Пусть (f(x)) — неотрицательная и непрерывная на отрезке ([a, b]) функция, (T = {x_{i}, i = overline{0, n}}) — разбиение отрезка ([a, b]), (L_{T}) — ломаная с вершинами (A_{i}(x_{i}, f(x_{i})), i = overline{0, n}), соединяющая последовательно точки (A_{0}, A_{1}, ldots A_{n}) (рис. 37.8), (l_{i}) — длина отрезка (mathcal{L}_{i} = [A_{i-1}, A_{i}]) — (i)-го звена ломаной (L_{T}). Тогда
$$
l_{i} = sqrt{(x_{i}-x_{i-1})^{2} + (f(x_{i})-f(x_{i-1}))^{2}}.label{ref27}
$$
При вращении вокруг оси (Ox) звена (mathcal{L}_{i}) образуется боковая поверхность усеченного конуса (цилиндра в случае, когда (f(x_{i}) = f(x_{i-1}))). Площадь этой поверхности, как известно из курса элементарной геометрии, равна
$$
p_{i} = pi (y_{i} + y_{i-1})l_{i},quad y_{k} = f(x_{k}),quad k = overline{1, n},nonumber
$$
откуда следует, что площадь (mathcal{P}_{T}) поверхности, получаемой при вращении ломаной (L_{T}) вокруг оси (Ox), равна
$$
mathcal{P}_{T} = sum_{i=1}^{n}(y_{i} + y_{i-1})l_{i}.label{ref28}
$$
Если существует
$$
lim_{l(T) rightarrow 0} mathcal{P}_{T} = mathcal{P}.label{ref29}
$$
где (l(T)) — мелкость разбиения (T), а (mathcal{P}_{T}) определяется формулой eqref{ref28}, то число (mathcal{P}) называют площадью поверхности вращения, то есть площадью поверхности, образующейся при вращении вокруг оси (Ox) графика функции (y = f(x), a leq x leq b).
Утверждение 7.
Если функция (f) имеет непрерывную производную на отрезке ([a, b]), то предел eqref{ref29} существует, а площадь (mathcal{P}) поверхности вращения выражается формулой
$$
mathcal{P} = 2pi intlimits_a^b f(x) sqrt{1 + (f'(x))^{2}} dx.label{ref30}
$$
Доказательство.
(circ) Из формул eqref{ref28} и eqref{ref27} следует, что
$$
mathcal{P}_{T} = pisum_{i=1}^{n}sqrt{(x_{i}-x_{i-1})^{2} + (y_{i}-y_{i-1})^{2}}(y_{i} + y_{i-1}),label{ref31}
$$
где (y_i=f(x_i)). По теореме Лагранжа
$$
y_{i}-y_{i-1} = f'(xi_{i})Delta x_{i},label{ref32}
$$
где (xi_{i} in Delta_{i} = [x_{i-1}, x_{i}]), (Delta x_{i} = x_{i}-x_{i-1}). Поэтому формулу eqref{ref28} можно записать в виде
$$
mathcal{P}_{T} = pi sum_{i=1}^{n}(y_{i} + y_{i-1}) sqrt{1 + (f'(xi_{i}))^{2}}Delta x_{i}.label{ref33}
$$
Прибавим и вычтем в правой части равенства eqref{ref33} интегральную сумму для интеграла eqref{ref30}, соответствующую разбиению (T) и выборке (xi = xi_{i} (i = overline{1, n})), указанной формулой eqref{ref32}, то есть сумму
$$
sigma_{T} (xi, g)= 2pi sum_{i=1}^{n}(f(xi_{i}))sqrt{1 + (f'(xi_{i}))^{2}}Delta x_{i}.label{ref34}
$$
где (g(x) = 2pi f(x)displaystylesqrt{1 + (f'(x))^{2}}). Заметим, что в силу непрерывности функции (g) для любой выборки (xi) существует
$$
lim_{l(T) rightarrow 0} sigma_{T} (xi, g) = 2pi intlimits_a^b f(x) sqrt{1 + (f'(x))^{2}} dx.nonumber
$$
Поэтому для доказательства формулы eqref{ref30} достаточно показать, что
$$
omega = mathcal{P}_{T}-sigma_{T} (xi, g) rightarrow 0 mbox{при} l(T) rightarrow 0.label{ref35}
$$
Из eqref{ref33} и eqref{ref34} следует, что
$$
omega = pi sum_{i=1}^{n}(y_{i} + y_{i-1}-2f(xi_i)) sqrt{1 + (f'(xi_{i}))^{2}}Delta x_{i}.label{ref36}
$$
При оценке величины (omega) воспользуемся тем, что функция (a) равномерно непрерывна на отрезке ([a, b]), то есть для любого (varepsilon > 0) существует (delta_{varepsilon} > 0) такое, что для любых точек (x’), (x″) из отрезка ([a, b]), удовлетворяющих условию (|x’-x″| < delta_{varepsilon}), выполняется неравенство
$$
|f(x’)-f(x″)| < frac{varepsilon}{C}.label{ref37}
$$
где число (C > 0) будет выбрано ниже.
Пусть разбиение (T) удовлетворяет условию (l(T) = displaystylemax_{1 leq i leq n} Delta x_{i} < delta_{varepsilon}); тогда (|x_{i}-xi_{i}| leq l(T) < delta_{varepsilon}), (|x_{i-1}-xi_{i}| leq l(T) < delta_{varepsilon}), так как (xi_{i} in Delta_{i}). Из eqref{ref37} следует, что
$$
|y_{i}-f(xi_{i})| = |f(x_{i})-f(xi_{i})| < frac{varepsilon}{C},quad |y_{i-1}-f(xi_{i})| < frac{varepsilon}{C},nonumber
$$
и поэтому
$$
|y_{i} + y_{i-1}-2f(xi_{i})| < frac{2varepsilon}{C}.label{ref38}
$$
В силу непрерывности функции (f'(x)) на отрезке ([a, b]) существует число (M > 0) такое, что (0 < displaystylesqrt{1 + (f'(x))^{2}} < M) для всех (x in [a, b]) и, в частности,
$$
0 < sqrt{1 + (f'(xi_{i}))^{2}} < M,quad i = overline{1, n}.label{ref39}
$$
Из eqref{ref36}, eqref{ref38} и eqref{ref39} получаем следующую оценку:
$$
|omega| < pi sum_{i=1}^{n} frac{2varepsilon}{C} M Delta x_{i} = frac{2pi M (b-a)}{C}varepsilon.label{ref40}
$$
Возьмем (C = 2pi M (b-a)) в условии eqref{ref37}; тогда из eqref{ref40} следует, что для любого (varepsilon > 0) существует (delta_{varepsilon} > 0) такое, что для каждого разбиения (T), мелкость (l(T)) которого удовлетворяет условию (l(T) < delta_{varepsilon}), выполняется неравенство (|omega| < varepsilon). Это означает, что (omega rightarrow 0) при (l(T) rightarrow 0). Формула eqref{ref30} доказана. (bullet)
Пример 7.
Пользуясь формулой eqref{ref30}, вычислить площадь (mathcal{P}) поверхности сферического пояса высоты (h), если радиус сферы равен (R).
Решение.
(triangle) Сферический пояс высоты (h) можно получить вращением дуги полуокружности, заданной уравнением (y = f(x) = displaystylesqrt{R^{2}-x^{2}}, a leq x leq b), где ([a, b] subset [-R, R], b-a = h), вокруг оси (Ox) (рис. 37.9). Так как (f'(x) =-displaystylefrac{x}{sqrt{R^{2}-x^{2}}}), то (1 + (f'(x))^{2} = displaystylefrac{R^{2}}{R^{2}-x^{2}}), (f(x)sqrt{1 + (f'(x))^{2}} = R) и по формуле eqref{ref30} получаем (mathcal{P}_{T} = 2pi displaystyleintlimits_a^b R dx = 2pi R(b-a) = 2pi Rh). В частности, площадь поверхности сферы радиуса (R) равна (4pi R^{2}). (blacktriangle)
Применение определенного интеграла при решении физических задач.
Определенный интеграл широко применяется при решении различных физических задач. С помощью определенного интеграла можно вычислять: путь, пройденный материальной точкой, если известна скорость движения; работу переменной силы; силу давления жидкости на плоскую фигуру; статические моменты и координаты центра масс плоской кривой и плоской фигуры и так далее.
Пусть плоская пластинка (G), имеющая форму криволинейной трапеции, определяемой условиями eqref{ref1}, погружена вертикально в жидкость с плотностью (rho) так, что ее боковые стороны параллельны поверхности жидкости и удалены от уровня жидкости на расстояния (a) и (b) (рис. 37.10). Требуется найти силу давления жидкости на пластинку.
Из курса физики известно, что если пластинка погружена в жидкость и расположена горизонтально на расстоянии (h) от поверхности жидкости, то сила давления (mathcal{P}) на одну из сторон пластинки равна
$$
mathcal{P} = g rho hS,nonumber
$$
где (S) — площадь пластинки, (g) — ускорение силы тяжести. Таким образом, сила давления — линейная функция от глубины погружения пластинки. Поэтому естественно разбить пластинку (G) на части прямыми, параллельными поверхности жидкости (оси (Oy)).
Пусть (T = {x_{i}, i = overline{0, n}}) — разбиение отрезка ([a, b]). Прямыми, проведенными через точки (x_{i} (i = overline{1, n-1})), разобьем фигуру (G) на (n) частей (полосок) (G_{i} (i = overline{1, n})). Выделим полоску (G_{i}), ограниченную прямыми (x = x_{i-1}) и (x = x_{i}) (рис. 37.10). Площадь этой полоски приближенно равна площади прямоугольника с основанием (Delta x_{i}) и высотой (f(x_{i})), глубину погружения всех точек полоски (G_{i}) можно считать равной (x_{i}). Поэтому сила давления жидкости на полоску (G_{i}) приближенно равна
$$
g rho x_{i}f(x_{i})Delta x_{i},nonumber
$$
а сумма
$$
mathcal{P}_{T} = sum_{substack{i=1}}^{substack{n}} g rho x_{i}f(x_{i})Delta x_{i}nonumber
$$
приближенно равна силе давления жидкости на пластинку (G).
Если (l(T) rightarrow 0), где (l(T)) — мелкость разбиения (T), а функция (f) непрерывна на отрезке ([a, b]), то (mathcal{P}_{T} rightarrow mathcal{P}), где
$$
mathcal{P} = g intlimits_a^b rho x f(x) dx.label{ref41}
$$
Число (mathcal{P}) выражаемое формулой eqref{ref41}, называют силой давления жидкости на пластинку (G).
Пример 8.
Вычислить силу давления (mathcal{P}) жидкости с плотностью (rho) на вертикальную стенку, имеющую форму полукруга радиуса (R) и погруженную в жидкость так, что диаметр полукруга расположен на поверхности жидкости (рис. 37.11).
Решение.
(triangle) Выберем систему координат так, как указано на рис. 37.11. Пользуясь формулой eqref{ref41}, где (f(x) = sqrt{R^{2}-x^{2}}, a = 0, b = R), получаем
$$
mathcal{P} = 2g rho intlimits_0^R x sqrt{R^{2}-x^{2}} dx =-left.frac{2}{3} g rho (R^{2}-x^{2})^{3/2}right|_{0}^{R} = frac{2rho g}{3} R^{3}. blacktrianglenonumber
$$
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
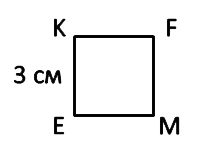
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
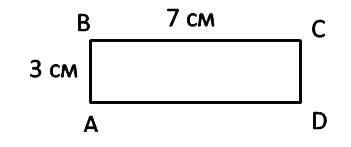
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
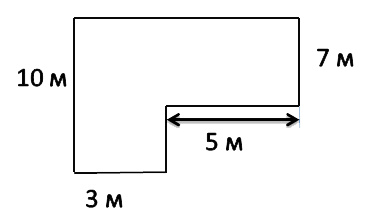
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
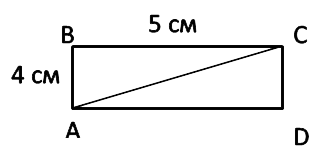
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Зависит от того, пересекаются ли эти прямоугольники или нет. Если же ко всему прочему эти прямоугольники произвольно “ориентированы” на плоскости, то задача усложняется еще больше.
В целом алгоритм простой:
1) Находим сумму площадей прямоугольников (S0)
2) Находим сумму площадей попарных пересечений прямоугольников (S1)
3) Находим сумму площадей попарных пересечений фигур из п. 2 (S2) и т. д.
Ответом будет сумма: S0 – S1 + S2 – S3 + .
Либо можно поступить просто. Если прямоугольники расположены достаточно “компактно”, то можно найти вмещающий их прямоугольник, в нем случайным образом накидать N точек, из этого множества выделить n точек, попавших внутрь какого-нибудь из интересующих нас прямоугольников, и полученное отношение n/N даст оценку площади (метод Монте-Карло).
Либо можно избавиться от вероятностного характера оценки из предыдущего пункта, введя на вмещающем прямоугольнике дискретную двумерную сетку с шагом h, и подсчитав количество узлов сетки, попавших внутрь рассматриваемых прямоугольников. Но вычислительная сложность этого алгоритма будет O((1/h)^2).
