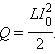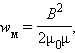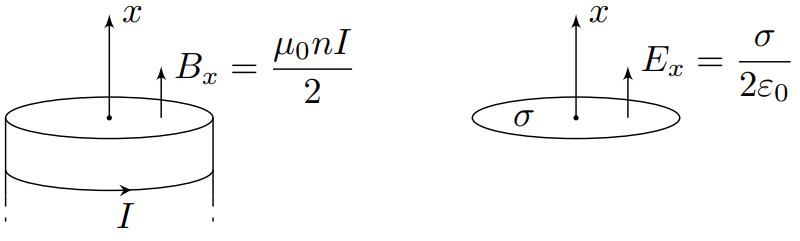Как найти площадь одного витка соленоида - Сайт, где вы сможете решить свои вопросы

Окей, остальные задачки:

1) Магнитное поле в центре кругового витка вычисляется по формуле B = μₒI/2R, откуда по известной индукции и известному радиусу враз находится величина тока. Плотность тока – это ток делить на площадь сечения проводника. Площадь сумеете сосчитать?

2) Индуктивность соленоида можно выразить не только через его длину и число витков (как у Габбаса), но и через длину намотки (l) и плотность намотки (n): L = μₒn²lS. Слова “из прилегающих вплотную” как раз и дают плотность намотки – не забудьте выразить её в числе витков на метр. Индуктивность и магнитный поток Ф внутри соленоида связаны простым соотношением Ф = IL, a индукция через магнитный поток – как B = ФS. Стало быть, индукция магнитного поля внутри соленоида связана с током как B = ILS, При этом площадь сечения соленоида равна πr² (r – тот самый радиус, который надо найти). Отсюда ток I = B/LS = B/Lπr².

В свою очередь, ток, по закону Ома, равен U/R, a R = ρl/s (l – длина проводника, s – его сечение). Полная длина проводника тут – это число витков умножить на длину одного витка, а длина одного витка = 2πr. Число витков N известно, поскольку длина соленоида и шаг витков в задачке указаны. Значит, ток от радиуса зависит как I = U/R = U/(ρl/s) = U/(ρN*2πr/s).

Приравнивая два выражения для тока друг к другу, можно найти радиус.

4) Полное индуктивное сопротивление Z = R + jωL + 1/jωC = R+j(ωL-1/ωC). Из этой формуле можно получить и выражение для его модуля – уж потрудитесь сделать это самостоятельно. Оный же модуль вычисляется из условия задачки по тому же закону Ома. И если приравнять два полученных модуля друг другу, то получится уравнение относительно L. Не штука.

Источник

Условие задачи:

Соленоид, содержащий 1000 витков медной проволоки сечением 0,2 мм², находится в однородном магнитном поле с осью, параллельной линиям магнитной индукции. Индукция магнитного поля равномерно изменяется со скоростью 0,01 Тл/с. Диаметр соленоида 5 см. Определить тепловую мощность, выделяющуюся в соленоиде, концы которого замкнуты между собой.

Задача №8.4.53 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(N=1000), (S_{пр}=0,2) мм², (alpha = 0^circ), (frac{Delta B}{Delta t}=0,01) Тл/с, (d=5) см, (W-?)

Решение задачи:

Тепловую мощность (W), выделяющуюся в соленоиде при протекании по нему электрического тока, можно определить по такой формуле:

[W = {I^2}R;;;;(1)]

Силу индукционного тока в контуре (I) будем искать, используя закон Ома:

[I = frac{{rm E_i}}{R};;;;(2)]

Подставим выражение (2) в формулу (1), тогда получим:

[W = frac{{{rm E}_i^2}}{R};;;;(3)]

Согласно закону Фарадея для электромагнитной индукции, ЭДС индукции, возникающая в соленоиде при изменении магнитного потока, пересекающего этот соленоид, равна по модулю скорости изменения магнитного потока. Учитывая, что соленоид содержит (N) витков, имеем:

[{{rm E}_i} = Nfrac{{Delta Phi }}{{Delta t}};;;;(4)]

Следует отметить, что для определения мгновенного значения ЭДС индукции по этой формуле интервал времени (Delta t) должен стремиться к нулю, в противном случае Вы получите среднее значение ЭДС индукции. Будем считать, что в нашем случае магнитный поток изменялся равномерно, поэтому интервал времени (Delta t) может быть каким угодно – среднее и мгновенное значения ЭДС индукции в таком случае будут одинаковы.

Модуль изменения магнитного потока (Delta Phi) будем определять по формуле (изменение магнитного потока происходило за счёт изменения величины магнитной индукции):

[Delta Phi = Delta BScos alpha ]

Здесь угол (alpha) – угол между осью соленоида и вектором магнитной индукции, равный по условию (alpha = 0^circ), то есть (cos alpha = 1). Тогда:

[Delta Phi = Delta BS ]

Полученное выражение подставим в (4):

[{{rm E}_i} = frac{{NDelta BS}}{{Delta t}}]

А это выражение подставим в (3):

[W = {left( {frac{{Delta B}}{{Delta t}}} right)^2}frac{{{N^2}{S^2}}}{R};;;;(5)]

Общее сопротивление соленоида можно найти по формуле:

[R = rho frac{{Npi d}}{{{S_{пр}}}};;;;(6)]

В этой формуле (rho) – удельное электрическое сопротивление меди, равное 17 нОм·м.

Площадь одного витка соленоида (S) равна:

[S = frac{{pi {d^2}}}{4};;;;(7)]

Выражения (6) и (7) подставим в формулу (5):

[W = {left( {frac{{Delta B}}{{Delta t}}} right)^2}frac{{{N^2}{pi ^2}{d^4}{S_{пр}}}}{{16rho Npi d}}]

[W = {left( {frac{{Delta B}}{{Delta t}}} right)^2}frac{{Npi {d^3}{S_{пр}}}}{{16rho }}]

Задача решена в общем виде, посчитаем ответ:

[W = frac{{{{0,01}^2} cdot 1000 cdot 3,14 cdot {{0,05}^3} cdot 0,2 cdot {{10}^{ – 6}}}}{{16 cdot 17 cdot {{10}^{ – 9}}}} = 28,9 cdot {10^{ – 6}};Вт = 28,9;мкВт]

Ответ: 28,9 мкВт.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.4.52 При равномерном изменении силы тока через катушку из 500 витков в ней возникает
8.4.54 Какой ток идет через гальванометр с сопротивлением 100 Ом, присоединенный
8.4.55 Два металлических стержня расположены вертикально и замкнуты вверху проводником

Источник

;

, (9)

где
– число витков на единицу длины;
объем соленоида.

Индуктивность
соленоида пропорциональна квадрату
числа витков на единицу его длины, объему
соленоида и магнитной проницаемости
вещества сердечника соленоида.

ЭДС
самоиндукции,
возникающая в катушке с постоянным
значением индуктивности,

,
при
L
=
const

,
(10)

т.е. ЭДС самоиндукции
прямо пропорциональна индуктивности
катушки и скорости изменения силы тока
в ней.

Из
аналогии

следует физический
смысл индуктивности:
индуктивность
контура является мерой
инертности
контура по отношению к изменению тока
в контуре.

Глава 1. Электродинамика

Магнитное поле

1.21. Самоиндукция. Энергия магнитного
поля

Самоиндукция
является важным частным случаем
электромагнитной индукции, когда
изменяющийся магнитный поток, вызывающий
ЭДС индукции, создается током в самом
контуре. Если ток в рассматриваемом
контуре по каким-то причинам изменяется,
то изменяется и магнитное поле этого
тока, а, следовательно, и собственный
магнитный поток, пронизывающий контур.
В контуре возникает ЭДС самоиндукции,
которая согласно правилу Ленца
препятствует изменению тока в контуре.

Собственный
магнитный
поток Φ,
пронизывающий контур или катушку с
током, пропорционален силе тока I:

Φ
= LI.

Коэффициент
пропорциональности L
в этой формуле называется коэффициентом
самоиндукции
или индуктивностью
катушки. Единица индуктивности в СИ
называется генри
(Гн). Индуктивность контура или катушки
равна 1 Гн, если при силе постоянного
тока 1 А собственный поток равен 1 Вб:

1 Гн = 1 Вб / 1 А.

В
качестве примера рассчитаем индуктивность
длинного соленоида, имеющего N
витков, площадь сечения S
и длину l.
Магнитное поле соленоида определяется
формулой (см. § 1.17)

B
= μ₀In,

где
I
– ток в соленоиде, n = N / e
– число витков на единицу длины соленоида.

Магнитный
поток, пронизывающий все N
витков соленоида, равен

Φ
= B·S·N
= μ₀n²SlI.

Следовательно, индуктивность соленоида
равна

L
= μ₀n²Sl
= μ₀n²V,

где
V
= Sl
– объем соленоида, в котором сосредоточено
магнитное поле. Полученный результат
не учитывает краевых эффектов, поэтому
он приближенно справедлив только для
достаточно длинных катушек. Если соленоид
заполнен веществом с магнитной
проницаемостью μ,
то при заданном токе I
индукция магнитного поля возрастает
по модулю в μ раз (см. §
1.17); поэтому
индуктивность катушки с сердечником
также увеличивается в μ раз:

L_μ
= μL
= μ₀μn²V.

ЭДС
самоиндукции,
возникающая в катушке с постоянным
значением индуктивности, согласно
формуле
Фарадеяравна

ЭДС
самоиндукции прямо пропорциональна
индуктивности катушки и скорости
изменения силы тока в ней.

Магнитное
поле обладает энергией. Подобно тому,
как в заряженном конденсаторе имеется
запас электрической энергии, в катушке,
по виткам которой протекает ток, имеется
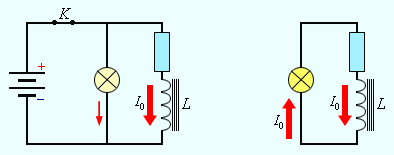
запас магнитной энергии. Если включить
электрическую лампу параллельно катушке
с большой индуктивностью в электрическую
цепь постоянного тока, то при размыкании
ключа наблюдается кратковременная
вспышка лампы (рис. 1.21.1). Ток в цепи
возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при
этом в электрической цепи, является
магнитное поле катушки.

Рисунок
1.21.1.

Магнитная
энергия катушки. При размыкании ключа
K
лампа ярко вспыхивает.

Из
закона сохранения энергии следует, что
вся энергия, запасенная в катушке,
выделится в виде джоулева тепла. Если
обозначить через R
полное сопротивление цепи, то за время
Δt
выделится количество теплоты ΔQ = I²RΔt.

Ток в цепи равен

Выражение
для ΔQ
можно записать в виде

ΔQ
= –LIΔI
= –Φ(I)ΔI.

В
этом выражении ΔI < 0;
ток в цепи постепенно убывает от
первоначального значения I₀
до нуля. Полное количество теплоты,
выделившейся в цепи, можно получить,
выполнив операцию интегрирования в
пределах от I₀до 0. Это дает

Эту
формулу можно получить графическим
методом, изобразив на графике зависимость
магнитного потока Φ(I)
от тока I
(рис. 1.21.2). Полное количество выделившейся
теплоты, равное первоначальному запасу
энергии магнитного поля, определяется
площадью изображенного на рис. 1.21.2
треугольника.

Рисунок
1.21.2.

Вычисление
энергии магнитного поля.

Таким
образом, энергия W_м
магнитного поля катушки с индуктивностью
L,
создаваемого током I,
равна

Применим
полученное выражение для энергии катушки
к длинному соленоиду с магнитным
сердечником. Используя приведенные
выше формулы для коэффициента самоиндукции
L_μ
соленоида и для магнитного поля B,
создаваемого током I,
можно получить:

где
V– объем соленоида. Это выражение
показывает, что магнитная энергия
локализована не в витках катушки, по
которым протекает ток, а рассредоточена
по всему объему, в котором создано
магнитное поле. Физическая величина

равная
энергии магнитного поля в единице
объема, называется объемной
плотностью магнитной энергии.
Дж. Максвелл
показал, что выражение для объемной
плотности магнитной энергии, выведенное
здесь для случая длинного соленоида,
справедливо для любых магнитных полей.

Источник

1
^??

Точки $A$ и $C$ расположены в плоскости витка на расстояниях $r/3$ и $3r$ соответственно от оси симметрии системы.

Найдите проекции индукции $B_{Ax}$ и $B_{Cx}$ магнитного поля, создаваемого соленоидом в точках $A$ и $C$ соответственно.

$$large{textbf{Первое решение}}

$$

Добавим к исходному соленоиду такой же, дополнив его до бесконечного.

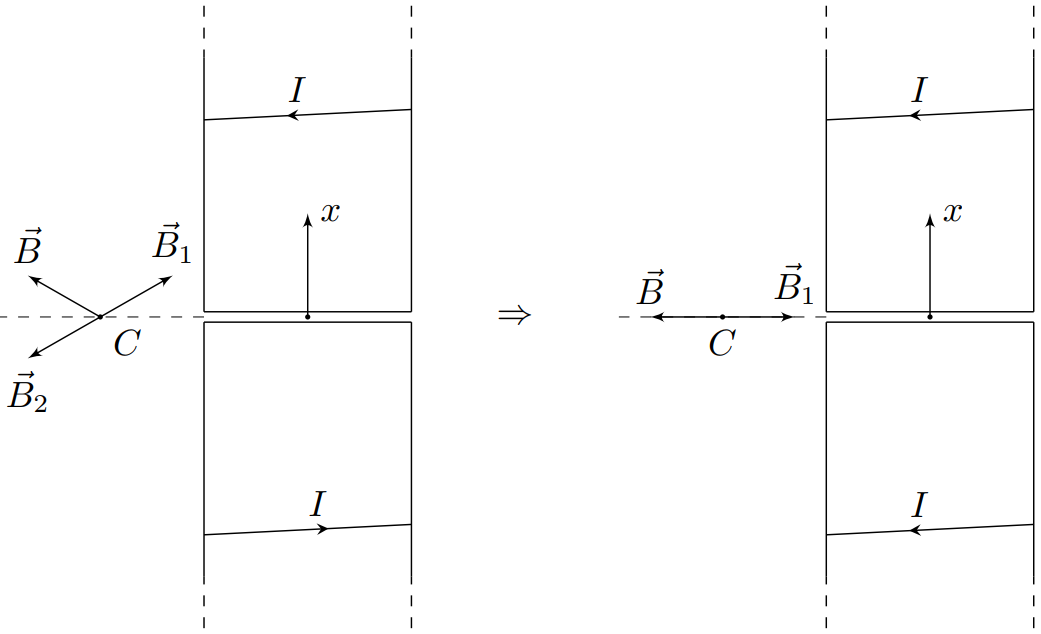
Обозначим магнитные поля исходного и добавленного соленоидов за $vec{B}$ и $vec{B}_1$ соответственно.

Если направление силы тока в добавленном соленоиде изменить на противоположное, то и создаваемое им магнитное поле $vec{B}_2$ изменится на противоположное, т.е $vec{B}_2=-vec{B}_1$.

Добавленный соленоид с изменённым на противоположное направлением силы тока симметричен исходному относительно основания, поэтому создаваемые добавленным и исходным соленоидами магнитные поля $vec{B}_2$ и $vec{B}$ соответственно будут также симметричны относительно основания.

Рассмотрим в точки, принадлежащие основанию.

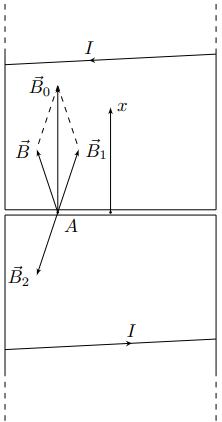
На рис.1 показаны исходный соленоид и добавленный с противоположным направлением тока.

Поскольку внутри соленоида магнитное поле $vec{B}_0$ однородно, имеем:

$$B_x+B_{1x}=B_0{.}

$$

Также, поскольку магнитные поля $vec{B}$ и $vec{B}_2$ симметричным относительно основания, имеем:

$$B_x+B_{2x}=0{.}

$$

Комбинируя полученные равенства, находим:

$$B_x=B_{1x}=displaystylefrac{B_0}{2}{.}

$$

Таким образом, в исходной ситуации в точке $A$ проекция магнитного поля на ось $x$ равна:

Рис.1.

Ответ:

$$B_{Ax}=displaystylefrac{mu_0nI}{2}{.}

$$

Рассмотрим в плоскости основания точки, не принадлежащие ему.

Поскольку магнитное поле вне бесконечного соленоида равно нулю:

$$vec{B}+vec{B}_1=0{.}

$$

Тогда $vec{B}_2=-vec{B}_1=vec{B}$. Поскольку векторы $vec{B}$ и $vec{B}_2$ симметричны относительно основания – в рассматриваемых точках магнитное поле направлено в плоскости основания, иначе $vec{B}_2neq{vec{B}}$ ⃗ (см.рис.2.)

Таким образом, в исходной ситуации в точке $C$ проекция магнитного поля на ось $x$ равна:

Рис.2.

Ответ:

$$B_{Cx}=0{.}

$$

$$large{textbf{Второе решение}}

$$

Второй вариант рассуждений может быть построен на использовании теоремы о телесном угле для магнитного поля. Если по плоскому слою течёт ток линейной плотностью $vec{i}$ , то в точке $O$ компонента магнитного поля, направленная вдоль слоя перпендикулярно $vec{i}$, равна:

$$B_{O||}=displaystylefrac{mu_0iOmega_O}{4pi}{,}

$$

где $Omega_O$– телесный угол, под которым виден слой из точки $O$.

Применяя теорему о телесном угле к осевой компоненте магнитного поля соленоида, получим:

$$B_x=displaystylefrac{mu_0nI Omega_text{бок}}{4pi}{,}

$$

где $Omega_text{бок}$ – телесный угол, под которым видна боковая поверхность соленоида(с учётом знака, данная величина может быть и отрицательна).

Отметим, что утверждения, данные в примечании к условию задачи, могут быть получены с помощью этой теоремы.

В точках, принадлежащих основанию, боковая поверхность соленоида видна под телесным углом $Omega_text{бок}=2pi$, а в точках, лежащих в плоскости основания и не принадлежащих ему, боковая поверхность соленоида видна под нулевым телесным углом. Отсюда получим ответы:

Ответ:

$$B_{Ax}=displaystylefrac{mu_0nI}{2}qquad B_{Cx}=0{.}

$$

2
^??

Найдите силу тока $I_text{в}$ в витке. Укажите, как он направлен.

Поскольку виток сверхпроводящий, магнитный поток, пронизывающий его, должен оставаться постоянным и равным нулю. Пусть $Phi_text{с}$ – магнитный поток через виток от соленоида. Выберем положительное направление силы тока в витке такое, как и в соленоиде, тогда:

$$Phi_text{с}+LI_text{в}=0{.}

$$

Как было показано в п.1, осевая компонента магнитного поля в плоскости витка на расстояниях меньших $r$ постоянна и равна $displaystylefrac{B_0}{2}$, а на расстояниях больших $r$ равна нулю. Поэтому поток магнитного поля соленоида через виток равен $Phi_text{с}=displaystylefrac{B_0S}{2}$, где $S$ – площадь основания соленоида.

С учетом $S=pi{r}^2$, находим:

$$Phi_text{с}=displaystylefrac{pimu_0nIr^2}{2}{,}

$$

и получаем ответ на второй вопрос:

Ответ:

$$I_text{в}=-displaystylefrac{pimu_0nIr^2}{2L}

$$

(ток в витке направлен против тока в обмотке соленоида).

3
^??

Найдите величину и направление силы магнитного взаимодействия, действующей на соленоид со стороны витка.

$$large{textbf{Первое решение}}

$$

Сила взаимодействия витка с соленоидом направлена вдоль их общей оси.

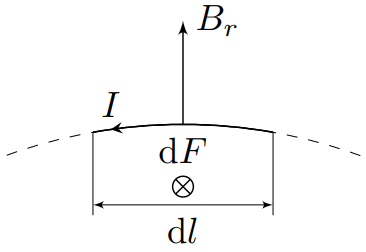
Пусть $B_r$ – компонента магнитного поля витка, направленная перпендикулярно боковой поверхности соленоида. Рассмотрим элемент тока соленоида длины $dl$. Будем искать силу притяжения витка к соленоиду. Осевая компонента силы Ампера, действующей на него, равна:

$$dF_{1x}=-IB_rdl{.}

$$

Рис.3.

В толщине слоя $dh$ находится $dN=ndh$ витков, а сила, действующая на них равна:

$$dF_x=dF_{1x}dN=-InB_rdldh{.}

$$

Отметим, что $dldh=dS_text{бок}$ – элемент площади боковой поверхности соленоида.

Тогда выражение для элемента силы можно переписать в виде:

$$dF_x=-IndPhi_text{бок}{,}

$$

где $Phi_text{бок}$ – поток магнитного поля витка через боковую поверхность соленоида.

Равнодействующая сила равна:

$$F_x=-InPhi_text{бок}{.}

$$

Для нахождения $Phi_text{бок}$ воспользуемся теоремой Гаусса для магнитного поля: через любую замкнутую поверхность поток магнитного поля равен нулю. Тогда имеем:

$$Phi_text{бок}+Phi_text{осн}=0{,}

$$

где $Phi_text{осн}$ – поток магнитного поля витка через основание соленоида.

Поскольку $rll{R}$, магнитное поле витка в ближнем основании соленоида можно считать однородным и равным:

$$B_{text{в}x}=displaystylefrac{mu_0I_text{в}}{2R}{.}

$$

Также, поскольку соленоид полубесконечный, в дальнем основании соленоида магнитное поле витка равняется нулю.

Тогда для $Phi_text{осн}$ имеем:

$$Phi_text{осн}=B_{text{в}x}S=displaystylefrac{mu_0I_text{в}S}{2R}{,}

$$

откуда находим:

Ответ:

$$F_x=-displaystylefrac{1}{RL}left(displaystylefrac{pimu_0nIr^2}{2}right)^2

$$

Соленоид и виток отталкиваются.

$textit{Примечание:}$ Отметим, что метод решения, использующий силу, действующую на виток с током в неоднородном магнитном поле, эквивалентен решению, описанному выше.

$$large{textbf{Второе решение}}

$$

На больших ($Rgg{r}$) расстояниях от основания полубесконечного соленоида источник магнитного потока $Phi_0=B_0S$ – ближний торец соленоида – выглядит практически точечным, и магнитный поток от него растекается практически равномерно по всем направлениям. Покажем это.

В соответствии с п.1 в основании соленоида проекция на ось $x$ создаваемого им магнитного поля постоянна и равна $B_x=displaystylefrac{mu_0nI}{2}$.

Изменение магнитного поля вне соленоида описывается теоремой Гаусса, а также теоремой о циркуляции для магнитного поля.

Поскольку токи вне соленоида отсутствуют, циркуляция магнитного поля по любому замкнутому контуру, не пересекающему поверхность соленоида, равна нулю.

Теми же уравнениями описывается электрическое поле тонкого диска, заряженного по поверхности с плотностью заряда $sigma$.

Действительно, проекция на ось $x$ электрического поля диска на его поверхности постоянна и равна $displaystylefrac{sigma}{2epsilon_0}$.

Поскольку вне диска электрические заряда отсутствуют, поток электрического поля через любую поверхность, не пересекающую плоскость диска, равен нулю. Циркуляция электрического поля по любому замкнутому контуру также равна нулю.

Рис.4.

В частности, убедимся в эквивалентности формул для $B_x$ и $E_x$ вне соленоида (рис.5.)

Рис.5.

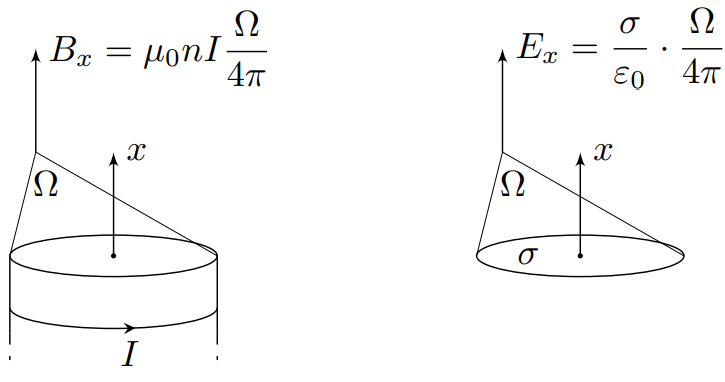
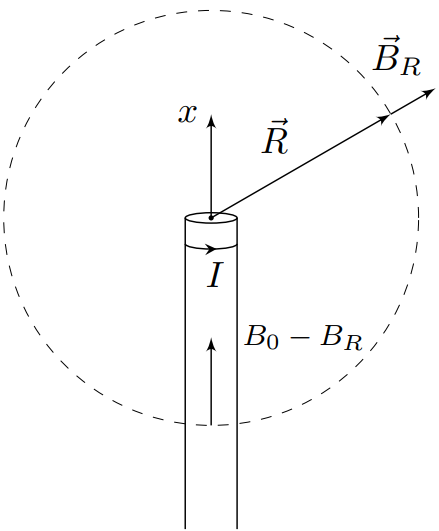
В соответствии с аналогией структур магнитного поля полубесконечного соленоида и электрического поля равномерно заряженного диска, на расстоянии $Rgg{r}$ от основания соленоида магнитное поле соленоида направленно вдоль линии, соединяющей рассматриваемую точку с основанием и равняется:

$$B_R=displaystylefrac{mu_0nIr^2}{4R^2}{.}

$$

Отметим, что изложенный вывод не противоречит теореме Гаусса для магнитного поля. Действительно, из теоремы о телесном угле для магнитного поля следует, что разность проекций магнитного поля внутри и вне соленоида на ось $x$ равна $B_0$. Применяя теорему Гаусса для сферической поверхности радиуса $Rgg{r}$ с центром в центре основания (см.рис.6), получим:

$$4pi{R}^2B_R=Phi_0=pi{r}^2B_0{,}

$$

что совпадает с полученным из аналогии результатом.

Рис.6.

Результирующая сила отталкивания, действующая на виток со стороны соленоида, равна:

$$F_{text{в}x}=-2pi{R}I_text{в}B_R=displaystylefrac{1}{RL}left(displaystylefrac{pimu_0nIr^2}{2}right)^2{,}

$$

откуда в соответствии с третьим законом Ньютона получим:

Ответ:

$$F_x=-displaystylefrac{1}{RL}left(displaystylefrac{pimu_0nIr^2}{2}right)^2{.}

$$

$$large{textbf{Третье решение}}

$$

Задача также допускает энергетическое решение.

Обозначим взаимную индуктивность соленоида и витка за $L_text{вз}=displaystylefrac{Phi_text{с}}{I}$.

В рассматриваемом положении она равна $displaystylefrac{mu_0nS}{2}$.

Если обозначить индуктивность соленоида $L_1$, то энергия системы равна

$$E=displaystylefrac{L_1I^2}{2}+displaystylefrac{LI^2_text{в}}{2}+L_text{вз}II_text{в}{,}

$$

или, с учетом соотношения $L_text{вз}I+LI_text{в}=0$:

$$E=displaystylefrac{L_1I^2}{2}-displaystylefrac{L^2_text{вз}I^2}{2L}{.}

$$

Изменение энергии системы равняется:

$$dE=-displaystylefrac{I^2L_text{вз}dL_text{вз}}{L}{.}

$$

При движении соленоида в нём возникает ЭДС индукции. Поскольку сила тока в соленоиде остаётся постоянной, источник, подключенный к соленоиду, компенсирует ЭДС индукции, а значит совершает работу.

Поток магнитного поля витка через соленоид равен

$$Phi_2=L_text{вз}I_text{в}=-displaystylefrac{L^2_text{вз}I}{L}{,}

$$

поэтому работа источника равна:

$$dA_text{ист}=-intlimits_0^{t}mathcal{E}_{инд}Idt=IdPhi_2=-displaystylefrac{2I^2L_text{вз}dL_text{вз}}{L}=-2dE{.}

$$

Пусть $F_x$ – сила, действующая на соленоид со стороны витка. Тогда внешняя сила, действующая на соленоид для поддержания его в равновесии равна $-F_x$.

При сдвиге соленоида на $dx$ изменение энергии системы равно

$$dA_text{ист}-F_xdx=dE{,}

$$

откуда

$$F_x=displaystylefrac{dE}{dx}=-displaystylefrac{I^2L_text{вз}}{L}displaystylefrac{dL_text{вз}}{dx}{.}

$$

Найдём изменение взаимной индуктивности $dL_text{вз}$ при сдвиге соленоида на расстояние $dx$ вдоль оси симметрии. Сдвиг эквивалентен наращиванию еще $dN=ndx$ витков соленоида вблизи торца. Тогда сверхпроводящий виток начинает создавать дополнительный поток $dPhi_1=B_{text{в}x}SdN$ через соленоид, а значит, изменение $L_text{вз}$ составит

$$dL_text{вз}=dleft(displaystylefrac{Phi_1}{I_text{в}}right)=displaystylefrac{mu_0Sndx}{2R}{.}

$$

В последнем выражении мы воспользовались магнитным полем витка в его центре.

Подставляя $L_text{вз}$ и $dL_text{вз}$ в выражение для $F_x$, находим:

Ответ:

$$F_x=-displaystylefrac{1}{RL}left(displaystylefrac{pimu_0nIr^2}{2}right)^2{.}

$$

$$large{textbf{Четвёртое решение}}

$$

Поиск работы источника можно обойти, замкнув подводящие к соленоиду провода накоротко. Тогда поток магнитного поля $Phi=left(L_1-displaystylefrac{L^2_text{вз}}{L}right)I$, пронизывающего соленоид, сохраняется при его перемещении.

Для энергии магнитного поля получим:

$$E=displaystylefrac{Phi^2}{2left(L_1-displaystylefrac{L^2_text{вз}}{L}right)}{.}

$$

При перемещении соленоида изменение энергии системы равняется

$$dE=frac{Phi^2}{left(L_1-displaystylefrac{L^2_text{вз}}{L}right)^2}frac{L_text{вз}dL_text{вз}}{L}=displaystylefrac{I^2L_text{вз}dL_text{вз}}{L}{.}

$$

Тогда для силы, действующей на соленоид со стороны витка, получим:

$$F_x=-displaystylefrac{dE}{dx}=-displaystylefrac{I^2L_text{вз}}{L}cfrac{dL_text{вз}}{dx}{.}

$$

Подставляя $L_text{вз}$ и $dL_text{вз}$ (см. третье решение) в выражение для $F_x$, находим:

Ответ:

$$F_x=-displaystylefrac{1}{RL}left(displaystylefrac{pimu_0nIr^2}{2}right)^2{.}

$$

Источник

Подробности: Обновлено 03.07.2018 17:41; Просмотров: 1451

Задачи по физике – это просто!

Не забываем, что решать задачи надо всегда в системе СИ!

А теперь к задачам!

Элементарные задачи из курса школьной физики на расчет индуктивности, самоиндукции, энергии магнитного поля тока.

Задача 1

Какова индуктивность витка проволоки, если при токе 6 А создается магнитный поток 12 мВб?

Задача 2

В катушке из 150 витков течет ток 7,5 А, и при этом создается магнитный поток 20 мВб.
Какова индуктивность катушки?

Задача 3

Через соленоид, индуктивность которого 0,4 мГн и площадь поперечного сечения 10 см², проходит ток 0,5 А.
Какова индукция поля внутри соленоида, если он содержит 100 витков?

Задача 4

Определить индуктивность контура с током 1,2 А, если контур ограничивает площадь 20 см², а магнитная индукция поля равна 0,8 Тл, причем вектор магнитной индукции направлен под углом 30^o к плоскости контура.