Как найти площадь одной грани тетраэдра - Сайт, где вы сможете решить свои вопросы

В данной публикации мы рассмотрим определение и разновидности тетраэдра, а также формулы для расчета площади его поверхности (одной грани и полной) и объема. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение тетраэдра
Виды тетраэдра
Формулы площади и объема правильного тетраэдра

Определение тетраэдра

Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.

Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.

Развертка тетраэдра на примере правильной фигуры представлена ниже:

Основные элементы и свойства тетраэдра (к нему применимы свойства правильной пирамиды) мы рассмотрели в отдельной публикации.

Виды тетраэдра

Равногранный тетраэдр – боковые грани фигуры равны, а основанием является правильный (равносторонний) треугольник.
Прямоугольный тетраэдр – угол между всеми тремя ребрами при одной вершине является прямым, т.е. равным 90°.
Правильный тетраэдр – все ребра равны, а грани, соответственно, являются равносторонними треугольниками.
Ортоцентричный тетраэдр – все высоты, проведенные из всех вершин фигуры к противолежащим граням, пересекаются в одной точке.

Формулы площади и объема правильного тетраэдра

Площадь поверхности

Объем

Источник

Тетраэдр,

или же частный случай треугольной пирамиды

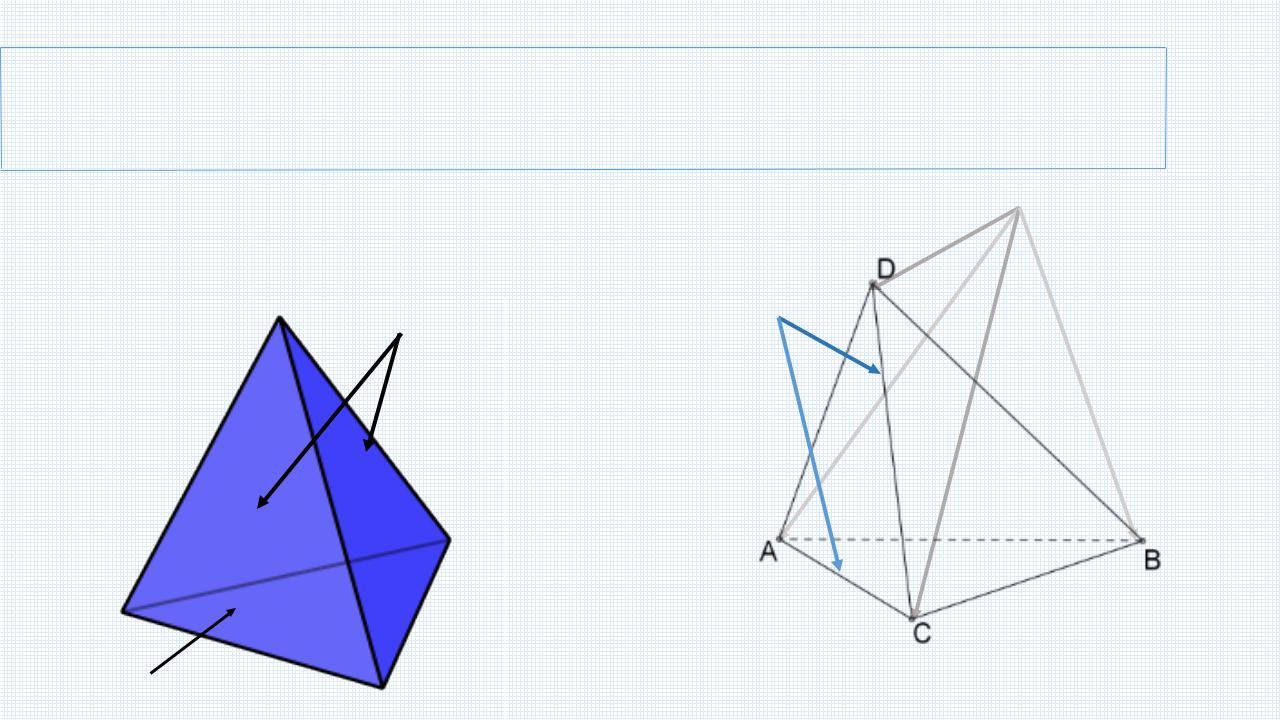
Что же такое этот «тетраэдр»?

Тетраэдр (от греческого «tetra» – «четыре» и «hedra» – «грань», иначе

говоря, четырехгранник) – простейший многогранник, гранями

которого являются четыре треугольника.

Вершины тетраэдра (всего 4)

	Ребра
	тетраэдра
Грани тетраэдра (всего 4)	(всего 6)

Два ребра тетраэдра, которые не

имеют общих вершин,

называются противоположными.

Основание тетраэдра	У тетраэдра 4 вершины, к каждой из них сходится 3 ребра.
Общее количество ребер у тетраэдра 6.

На самом деле, тетраэдры нас повсюду окружают
Например, в молекулярном		(Не в прямом смысле, конечно.)

мире в строении некоторых		А в живой природе
химических элементов, в		некоторые плоды, находясь
живой природе или в бытовой		вчетвером на одной кисти,
жизни.		располагаются в вершинах
Это – молекула метана CH ,	С	почти правильного
тетраэдра, как вот эти
которая, как мы видим,
	грецкие орехи.
имеет форму тетраэдра.

	А вот это грандиозное	Эта фигура также часто
	сооружение хоть и	используется человеком.
	выглядит страшно, но	Например, упаковка
	представляет собой	«Tetra Classic», в которую
	молекулу оксида цинка	в СССР помещали
	ZnO (синим цветом	молочные продукты,
	обведены тетраэдры в ее	также имеет форму
	строении) .	тетраэдра.

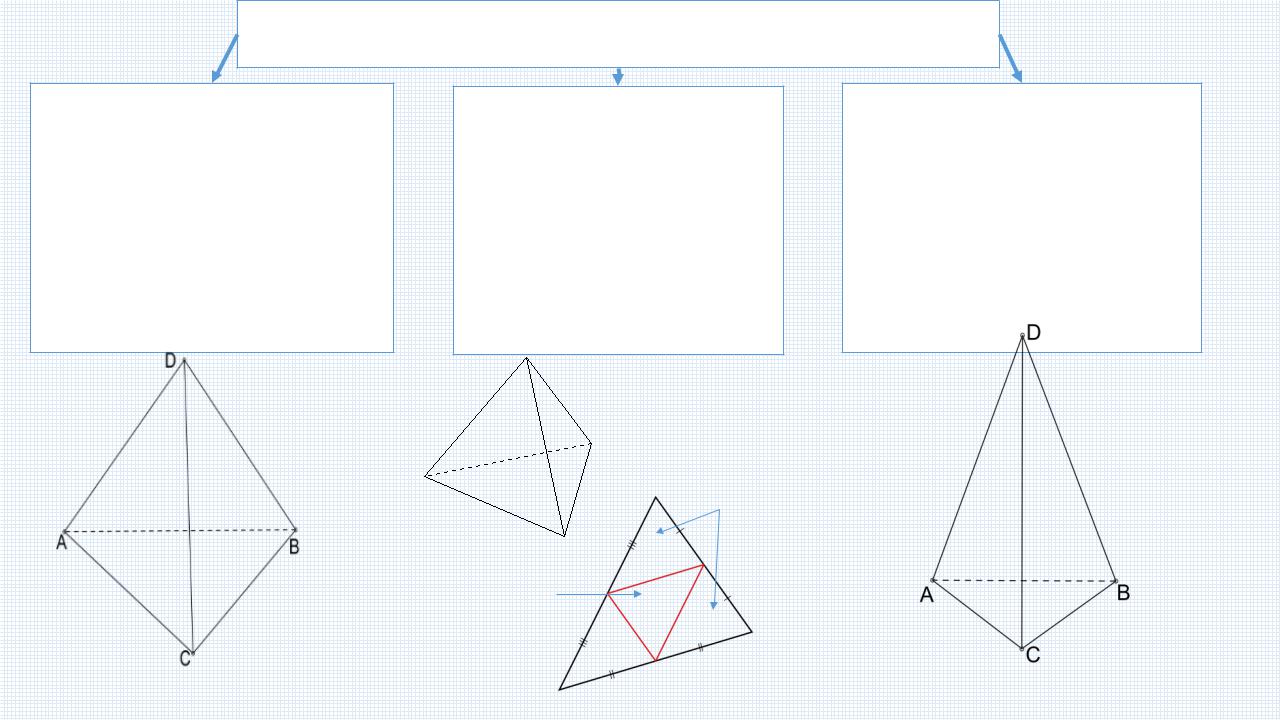
Основные виды тетраэдров
Правильный тетраэдр –		Равногранный	Правильная
это такая правильная		тетраэдр, у которого	треугольная пирамида,
треугольная пирамида,		все грани – равные	у которой одна грань —
каждая из граней которой		между собой	основание пирамиды —
является равносторонним		треугольники. Его	правильный треугольник,
треугольником. Все ребра		развертка	а остальные — боковые
такого тетраэдра имеют		представляет собой	грани — равные
равную длину, а грани –		четыре остроугольных	треугольники с общей
равную площадь.		треугольника.	вершиной
		D
		B
	А	Грани

		C
		Основание
		Развертка равногранного тетраэдра

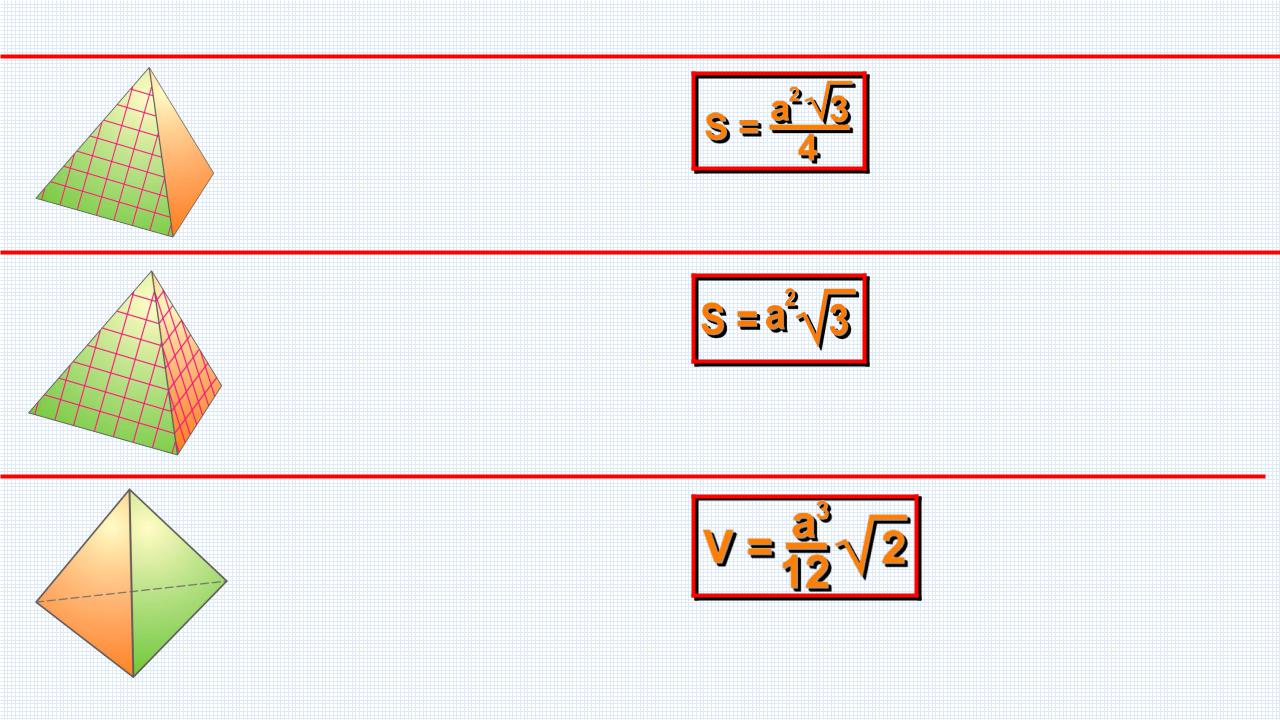
Основные формулы тетраэдра

1. Площадь одной грани тетраэдра

S – площадь одной грани

а– длина ребра тетраэдра

2.Площадь поверхности тетраэдра

S – площадь поверхности тетраэдра

а– длина ребра тетраэдра

3.Объем тетраэдра

V – объем тетраэдра

a – длина ребра тетраэдра

Основные формулы тетраэдра (продолжение)

4. Высота тетраэдра

h – высота тетраэдра

a – ребро тетраэдра

5. Радиус описанной

сферы тетраэдра.

R – радиус описанной сферы

a – ребро тетраэдра

6. Радиус вписанной

в тетраэдр сферы

r – радиус вписанной в тетраэдр сферы

a – ребро тетраэдра

Соседние файлы в папке Куча презентаций

#
#
#
#
#
14.01.20232.05 Mб0Тетраэдр.ppsx
#
#
#
#
#
#

Источник

Что такое тетраэдр: определение, виды, формулы площади и объема

Определение тетраэдра

Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.

Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.

Развертка тетраэдра на примере правильной фигуры представлена ниже:

Тетраэдр

Древние греки дали многограннику имя по числу граней. «Тетра» означает четыре, «хедра» – означает грань (тетраэдр – четырехгранник).

Поэтому на вопрос – “что такое тетраэдр?”, можно дать следующее определение: ” Тетраэдр это геометрическое тело из четырех граней, каждая их которых – правильный треугольник “.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .

Тетраэдр имеет следующие характеристики:

Тип грани – правильный треугольник;
Число сторон у грани – 3;
Общее число граней – 4;
Число рёбер, примыкающих к вершине – 3;
Общее число вершин – 4;
Общее число рёбер – 6;

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.

Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.

Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.

Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы тетраэдра определяется по формуле:

, где a – длина стороны.

Сфера может быть вписана внутрь тетраэдра.

Радиус вписанной сферы тетраэдра определяется по формуле:

Площадь поверхности тетраэдра

Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:

Объем тетраэдра определяется по следующей формуле:

Высота тетраэдра определяется по следующей формуле:

Расстояние до центра основания тетраэдра определяется по формуле:

Вариант развертки

Тетраэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка – единая деталь с линиями сгибов.

Древнегреческий философ Платон ассоциировал тетраэдр с “земным” элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.

Заметим, что это не единственный вариант развертки.

Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
– если Вы предполагаете распечатать на цветном принтере – цветная развертка
– если Вы предполагаете использовать для сборки цветной картон – развертка

Видео. Тетраэдр из набора “Волшебные грани”

Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора “Волшебные грани”.

Сборка многогранника из набора:

Подробная сборка от Алексея Жигулева (youtube-канал PRO)

вращение готового многогранника:

Видео. Вращение всех правильных многогранников

Тетраэдр.

Тетраэдр – это частный случай правильной треугольной пирамиды.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Медиана тетраэдра – это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).

Бимедиана тетраэдра – это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).

Высота тетраэдра – это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Типы тетраэдров.

Правильный тетраэдр – это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Правильный тетраэдр – это один из 5-ти правильных многогранников.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

– Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

– Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

– Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

– Каркасный тетраэдр — тетраэдр, который таким условиям:

есть сфера, которая касается каждого ребра,
суммы длин ребер, что скрещиваются равны,
суммы двугранных углов при противоположных ребрах равны,
окружности, которые вписаны в грани, попарно касаются,
каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.

– Соразмерный тетраэдр, бивысоты у него одинаковы.

– Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

Формулы для определения элементов тетраэдра.

Высота тетраэдра:

где h – высота тетраэдра, a – ребро тетраэдра.

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

где V – объем тетраэдра, a – ребро тетраэдра.

Основные формулы для правильного тетраэдра:

Где S – Площадь поверхности правильного тетраэдра;

h – высота, опущенная на основание;

r – радиус вписанной в тетраэдр окружности;

[spoiler title=”источники:”]

http://mnogogranniki.ru/tetraedr.html

http://www.calc.ru/1535.html

[/spoiler]

Источник

Площадь пирамиды

Гагик Оганесян

Эксперт по предмету «Калькуляторы»

Задать вопрос автору статьи

На этой странице вы сможете познакомиться с формулами для вычисления площади полной и боковой поверхности пирамиды. Также на страницу добавлены онлайн-калькуляторы и примеры вычисления площадей пирамид.

Определение 1

Пирамида представляет собой объёмную фигуру, в основании которой лежит многоугольник, а боковые грани являются треугольниками. У правильной пирамиды в основании лежит правильный многоугольник, а боковые грани равны.

Рассмотрим, как вычислять площадь полной поверхности правильной пирамиды.

Полная площадь поверхности пирамиды через высоту и сторону основания

Суммарная площадь всех сторон и основания правильной пирамиды определяется по формуле:

${S =frac{n cdot a}{2} cdot (frac{a}{2 cdot mathrm{tg}frac{180}{n}} + sqrt{H^2 + (frac{a}{2 cdot mathrm{tg}(frac{180}{n})})^2})}$

Здесь:

$a$ — длина стороны основания;

$n$ — число сторон основания;

$H$ — высота пирамиды.

Для вычисления полной поверхности правильного тетраэдра можно применять более простую формулу.

Полная площадь тетраэдра

Для правильного тетраэдра полная площадь поверхности определяется по формуле:

$S =sqrt3 cdot a^2$, где

$a$ — длина стороны тетраэдра.

Рассмотрим пример использования формулы для правильного тетраэдра.

Пример 1

Задача

Боковая грань правильного тетраэдра равна $7$ см. Чему равна площадь полной поверхности?

Решение:

Вспомним, чему равна площадь правильного треугольника:

$S_∆ = sqrt3 cdot frac{a^2}{4} = sqrt3 cdot frac{7^2}{4} ≈ 21.21$ кв. см.

Мы нашли площадь одной грани правильного тетраэдра. Всего у тетраэдра 4 грани, а это значит что вся площадь поверхности равна произведению площади одной грани на количество граней, равное четырём:

$S = 21.21 cdot 4 = 84,87$ кв. см.

Полученный ответ проверим онлайн-калькулятором. Результаты совпадают, а значит ответ — верный.

Боковую поверхность правильной пирамиды чаще всего вычисляют по двум формулам — через периметр и апофему или через сторону основания и высоту.

Определение 2

Апофемой пирамиды называется высота боковой грани.

Боковая поверхность пирамиды через периметр и апофему

Боковая поверхность правильной пирамиды в данном случае определяется по формуле:

$S_б = frac12 cdot P cdot c$, где

$P$ — периметр основания пирамиды;

$c$ — апофема пирамиды.

При этом периметр правильного многоугольника может быть определён по формуле:

$P = a cdot n$, где

$a$ — длина стороны многоугольника;

$n$ — количество сторон.

Вычислим боковую поверхность через апофему и периметр на примере 4-угольной пирамиды.

Пример 2

Задача

Дана правильная пирамида с квадратом в основании, сторона которого равна $5$ см. Апофема пирамиды равна $9$ см. Вычислите площадь боковой поверхности.

Решение:

Рассчитаем периметр основания. Для квадрата периметр равен умноженной на 4 стороне:

$P_{осн.} = 4 cdot a^2 = 20$ см

Теперь сосчитаем площадь боковой поверхности:

$S_б = frac12 cdot 20 cdot 9 = 90$ кв. см.

Боковая поверхность пирамиды через высоту и сторону основания

В случае если дана высота и сторона основания правильной пирамиды, площадь боковой поверхности рассчитывается по формуле:

$S_б = frac{n cdot a}{2} cdot sqrt{h^2 + (frac{a} {2 cdot mathrm{tg}(180 / n)})^2}$, здесь

$n$ — количество сторон основания;

$a$ — длина стороны основания;

$h$ — высота пирамиды.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата написания статьи: 27.06.2019

Источник

Тетра́эдр (др.-греч. τετράεδρον «четырёхгранник»^[1] ← τέσσαρες / τέσσερες / τέτταρες / τέττορες / τέτορες «четыре» + ἕδρα «седалище, основание») — простейший многогранник, гранями которого являются четыре треугольника^[2].

Тетраэдр является треугольной пирамидой при принятии любой из граней за основание.
У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным. Правильный тетраэдр является одним из пяти правильных многогранников.

Свойства[править | править код]

Параллельные плоскости, проходящие через три пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.

Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра, делит его на две равные по объёму части^[3]^:216-217.

Бимедианы тетраэдра пересекаются в той же самой точке, что и медианы тетраэдра.
- Бимедианами тетраэдра называют отрезки, соединяющие середины его скрещивающихся рёбер (не имеющих общих вершин).

Центры сфер, которые проходят через три вершины и инцентр, лежат на сфере, центр которой совпадает с центром описанной сферы.
- Также это утверждение верно и для внешних инцентров.

Плоскости, которые проходят через середину ребра и перпендикулярны противоположному ребру,пересекаются в одной точке (ортоцентр).
- Ортоцентр в симплексе определяется как пересечение гиперплоскостей, которые перпендикулярны ребру и проходят через центр тяжести противоположного элемента.

Центр сферы(F),которая проходит через центры тяжести граней тетраэдра, центр тяжести тетраэдра(M), центр описанной сферы(R) и ортоцентр (H) лежат на одной прямой. При этом .

Центр сферы (S) вписанный в дополнительный тетраэдр,центр сферы (N) вписанный в антидополнительный тетраэдр, центр тяжести тетраэдра (M) и центр вписанной сферы (I) лежат на одной прямой.

Пусть точка G₁ делит отрезок соединяющий ортоцентр(H) и вершину 1 в отношении 1:2. Опустим перпендикуляр с точки G₁ на грань противолежащей вершине 1. Перпендикуляр пересекает грань в точке W₁. Точки G₁ и W₁ лежат на сфере (сфере Фейербаха), которая проходит через центры тяжести граней тетраэдра.

Сечение плоскостью, проходящей через середины четырёх рёбер тетраэдра, является параллелограммом.

Типы тетраэдров[править | править код]

Равногранный тетраэдр[править | править код]

Развёртка равногранного тетраэдра

Все грани его представляют собой равные между собой треугольники. Развёрткой равногранного тетраэдра является треугольник, разделённый тремя средними линиями на четыре равных треугольника. В равногранном тетраэдре основания высот, середины высот и точки пересечения высот граней лежат на поверхности одной сферы (сферы 12 точек) (Аналог окружности Эйлера для треугольника).

Свойства равногранного тетраэдра:

Все его грани равны (конгруэнтны).
Скрещивающиеся рёбра попарно равны.
Трёхгранные углы равны.
Противолежащие двугранные углы равны.
Два плоских угла, опирающихся на одно ребро, равны.
Сумма плоских углов при каждой вершине равна 180°.
Развёртка тетраэдра — треугольник или параллелограмм.
Описанный параллелепипед прямоугольный.
Тетраэдр имеет три оси симметрии.
Общие перпендикуляры скрещивающихся рёбер попарно перпендикулярны.
Средние линии попарно перпендикулярны.
Периметры граней равны.
Площади граней равны.
Высоты тетраэдра равны.
Отрезки, соединяющие вершины с центрами тяжести противоположных граней, равны.
Радиусы описанных около граней окружностей равны.
Центр тяжести тетраэдра совпадает с центром описанной сферы.
Центр тяжести совпадает с центром вписанной сферы.
Центр описанной сферы совпадает с центром вписанной.
Вписанная сфера касается граней в центрах описанных около этих граней окружностей.
Сумма внешних единичных нормалей (единичных векторов, перпендикулярных к граням) равна нулю.
Сумма всех двугранных углов равна нулю.
Центры вневписанных сфер лежат на описанной сфере.

Ортоцентрический тетраэдр[править | править код]

Все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.

Высоты тетраэдра пересекаются в одной точке.
Основания высот тетраэдра являются ортоцентрами граней.
Каждые два противоположных ребра тетраэдра перпендикулярны.
Суммы квадратов противоположных рёбер тетраэдра равны.
Отрезки, соединяющие середины противоположных рёбер тетраэдра, равны.
Произведения косинусов противоположных двугранных углов равны.
Сумма квадратов площадей граней вчетверо меньше суммы квадратов произведений противоположных рёбер.
У ортоцентрического тетраэдра окружности 9 точек (окружности Эйлера) каждой грани принадлежат одной сфере (сфере 24 точек).
У ортоцентрического тетраэдра центры тяжести и точки пересечения высот граней, а также точки, делящие отрезки каждой высоты тетраэдра от вершины до точки пересечения высот в отношении 2:1, лежат на одной сфере (сфере 12 точек).

Прямоугольный тетраэдр[править | править код]

Все рёбра, прилежащие к одной из вершин, перпендикулярны между собой.
Прямоугольный тетраэдр получается отсечением тетраэдра плоскостью от прямоугольного параллелепипеда.

Каркасный тетраэдр[править | править код]

Это тетраэдр, отвечающий любому из следующих условий^[4]:

существует сфера, касающаяся всех рёбер,
суммы длин скрещивающихся рёбер равны,
суммы двугранных углов при противоположных рёбрах равны,
окружности, вписанные в грани, попарно касаются,
все четырёхугольники, получающиеся на развёртке тетраэдра, — описанные,
перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.

Соразмерный тетраэдр[править | править код]

У этого типа бивысоты равны.

Свойства соразмерного тетраэдра:

Инцентрический тетраэдр[править | править код]

У этого типа отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Свойства инцентрического тетраэдра:

Отрезки, соединяющие центры тяжести граней тетраэдра с противоположными вершинами (медианы тетраэдра), всегда пересекаются в одной точке. Эта точка — центр тяжести тетраэдра.
Замечание. Если в последнем условии заменить центры тяжести граней на ортоцентры граней, то оно превратится в новое определение ортоцентрического тетраэдра. Если же заменить их на центры вписанных в грани окружностей, называемых иногда инцентрами, мы получим определение нового класса тетраэдров — инцентрических.
Отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Биссектрисы углов двух граней, проведённому к общему ребру этих граней, имеют общее основание.
Произведения длин противоположных рёбер равны.
Треугольник, образованный вторыми точками пересечения трёх рёбер, выходящих из одной вершины, с любой сферой, проходящей через три конца этих рёбер, является равносторонним.

Правильный тетраэдр[править | править код]

Это равногранный тетраэдр, у которого все грани — правильные треугольники. Является одним из пяти платоновых тел.

Свойства правильного тетраэдра:

все рёбра тетраэдра равны между собой,
все грани тетраэдра равны между собой,
периметры и площади всех граней равны между собой.
Правильный тетраэдр является одновременно ортоцентрическим, каркасным, равногранным, инцентрическим и соразмерным.
Тетраэдр является правильным, если он принадлежит к двум любым видам тетраэдров из перечисленных: ортоцентрический, каркасный, инцентрический, соразмерный, равногранный.
Тетраэдр является правильным, если он является равногранным и принадлежит к одному из следующих видов тетраэдров: ортоцентрический, каркасный, инцентрический, соразмерный.
В правильный тетраэдр можно вписать октаэдр, притом четыре (из восьми) грани октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
Правильный тетраэдр состоит из одного вписанного октаэдра (в центре) и четырёх тетраэдров (по вершинам), причём рёбра этих тетраэдров и октаэдра вдвое меньше рёбер правильного тетраэдра.
Правильный тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба.
Правильный тетраэдр можно вписать в додекаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами додекаэдра.
Скрещивающиеся рёбра правильного тетраэдра взаимно перпендикулярны.

Объём тетраэдра[править | править код]

${displaystyle V={frac {1}{6}}{begin{vmatrix}1&x_{1}&y_{1}&z_{1}\1&x_{2}&y_{2}&z_{2}\1&x_{3}&y_{3}&z_{3}\1&x_{4}&y_{4}&z_{4}end{vmatrix}}={frac {1}{6}}{begin{vmatrix}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\x_{3}-x_{1}&y_{3}-y_{1}&z_{3}-z_{1}\x_{4}-x_{1}&y_{4}-y_{1}&z_{4}-z_{1}end{vmatrix}},}$

или

${displaystyle V={frac {1}{3}} SH,}$

где — площадь любой грани, а — высота, опущенная на эту грань.

Объём тетраэдра через длины рёбер выражается с помощью определителя Кэли-Менгера:

$288cdot V^{2}={begin{vmatrix}0&1&1&1&1\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\1&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{2}\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\1&d_{14}^{2}&d_{24}^{2}&d_{34}^{2}&0end{vmatrix}}.$

Эта формула имеет плоский аналог для площади треугольника в виде варианта формулы Герона через аналогичный определитель.
Объём тетраэдра через длины двух противоположных рёбер a и b, как скрещивающихся линий, которые удалены на расстояние h друг от друга и образуют друг с другом угол , находится по формуле:

${displaystyle V={frac {1}{6}}abhsin phi .}$

Объём тетраэдра через длины трёх его рёбер a, b и c, выходящих из одной вершины и образующих между собой попарно соответственно плоские углы , находится по формуле^[5]

${displaystyle V={frac {1}{6}} abc{sqrt {D}},}$

где

${displaystyle D={begin{vmatrix}1&cos gamma &cos beta \cos gamma &1&cos alpha \cos beta &cos alpha &1end{vmatrix}}.}$

Аналогом для плоскости последней формулы является формула площади треугольника через длины двух его сторон a и b, выходящих из одной вершины и образующих между собой угол :

$S={frac {1}{2}} ab{sqrt {D}},$

где
$D={begin{vmatrix}1&cos gamma \cos gamma &1\end{vmatrix}}.$

Замечание[править | править код]

Есть аналог формулы Герона для объёма тетраэдра ^[6]

Формулы тетраэдра в декартовых координатах в пространстве[править | править код]

Обозначения:

${displaystyle mathbf {r} _{1}(x_{1},y_{1},z_{1}),}$ ${displaystyle mathbf {r} _{2}(x_{2},y_{2},z_{2}),}$ ${displaystyle mathbf {r} _{3}(x_{3},y_{3},z_{3}),}$ ${displaystyle mathbf {r} _{4}(x_{4},y_{4},z_{4})}$ — координаты вершин тетраэдра.

Объём тетраэдра (с учётом знака):

${displaystyle V={frac {1}{6}}{begin{vmatrix}1&x_{1}&y_{1}&z_{1}\1&x_{2}&y_{2}&z_{2}\1&x_{3}&y_{3}&z_{3}\1&x_{4}&y_{4}&z_{4}end{vmatrix}}}$ .

Координаты центра тяжести (пересечение медиан): ${displaystyle mathbf {r} _{T}(x_{T},y_{T},z_{T})}$

${displaystyle x_{T}={frac {x_{1}+x_{2}+x_{3}+x_{4}}{4}};}$ ${displaystyle y_{T}={frac {y_{1}+y_{2}+y_{3}+y_{4}}{4}};}$ ${displaystyle z_{T}={frac {z_{1}+z_{2}+z_{3}+z_{4}}{4}}.}$

Координаты центра вписанной сферы: ${displaystyle mathbf {r} _{r}(x_{r},y_{r},z_{r})}$

${displaystyle x_{r}={frac {S_{1}x_{1}+S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}};}$ ${displaystyle y_{r}={frac {S_{1}y_{1}+S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}};}$ ${displaystyle z_{r}={frac {S_{1}z_{1}+S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}},}$

где $S_{1}$ — площадь грани, противолежащей первой вершине, ${displaystyle S_{2}}$ — площадь грани, противолежащей второй вершине и так далее.

Соответственно уравнение вписанной сферы:

${displaystyle (x-{frac {S_{1}x_{1}+S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(y-{frac {S_{1}y_{1}+S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(z-{frac {S_{1}z_{1}+S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2}=({frac {3V}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2},}$

Уравнение вневписанной сферы, противолежащей первой вершине:

${displaystyle (x-{frac {-S_{1}x_{1}+S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(y-{frac {-S_{1}y_{1}+S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(z-{frac {-S_{1}z_{1}+S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2}=({frac {3V}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2},}$

Уравнение вневписанной сферы, противолежащей первой и второй вершинам (количество таких сфер может варьироваться от нуля до трёх):

${displaystyle (x-{frac {-S_{1}x_{1}-S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2}+(y-{frac {-S_{1}y_{1}-S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2}+(z-{frac {-S_{1}z_{1}-S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2}=({frac {3V}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2},}$

Уравнение описанной сферы:

${displaystyle {begin{vmatrix}x^{2}+y^{2}+z^{2}&x&y&z&1\x_{1}^{2}+y_{1}^{2}+z_{1}^{2}&x_{1}&y_{1}&z_{1}&1\x_{2}^{2}+y_{2}^{2}+z_{2}^{2}&x_{2}&y_{2}&z_{2}&1\x_{3}^{2}+y_{3}^{2}+z_{3}^{2}&x_{3}&y_{3}&z_{3}&1\x_{4}^{2}+y_{4}^{2}+z_{4}^{2}&x_{4}&y_{4}&z_{4}&1end{vmatrix}}=0.}$

Формулы тетраэдра в барицентрических координатах[править | править код]

Обозначения:

${displaystyle mathbf {J} (alpha _{1},alpha _{2},alpha _{3},alpha _{4})=alpha _{1}mathbf {J_{1}} +alpha _{2}mathbf {J_{2}} +alpha _{3}mathbf {J_{3}} +alpha _{4}mathbf {J_{4}} ,}$ — барицентрические координаты.

Объём тетраэдра (с учётом знака): Пусть ${displaystyle mathbf {J} _{1}(x_{1},y_{1},z_{1},t_{1}),mathbf {J} _{2}(x_{2},y_{2},z_{2},t_{2}),mathbf {J} _{3}(x_{3},y_{3},z_{3},t_{3}),mathbf {J} _{4}(x_{4},y_{4},z_{4},t_{4}).}$ — координаты вершин тетраэдра.

Тогда

${displaystyle V={frac {begin{vmatrix}x_{1}&y_{1}&z_{1}&t_{1}\x_{2}&y_{2}&z_{2}&t_{2}\x_{3}&y_{3}&z_{3}&t_{3}\x_{4}&y_{4}&z_{4}&t_{4}\end{vmatrix}}{(x_{1}+y_{1}+z_{1}+t_{1})(x_{2}+y_{2}+z_{2}+t_{2})(x_{3}+y_{3}+z_{3}+t_{3})(x_{4}+y_{4}+z_{4}+t_{4})}}V',}$ где — объем базисного тетраэдра.

Координаты центра тяжести (пересечение медиан): ${displaystyle mathbf {J} _{T}(1,1,1,1).}$

Координаты центра вписанной сферы: ${displaystyle mathbf {J} _{r}(S_{1},S_{2},S_{3},S_{4}).}$

Координаты центра описанной сферы:

${displaystyle mathbf {J} _{R}={begin{vmatrix}0&mathbf {J_{1}} &mathbf {J_{2}} &mathbf {J_{3}} &mathbf {J_{4}} \1&0&alpha _{2,1}^{2}&alpha _{3,1}^{2}&alpha _{4,1}^{2}\1&alpha _{2,1}^{2}&0&alpha _{3,2}^{2}&alpha _{4,2}^{2}\1&alpha _{3,1}^{2}&alpha _{3,2}^{2}&0&alpha _{4,3}^{2}\1&alpha _{4,1}^{2}&alpha _{4,2}^{2}&alpha _{4,3}^{2}&0\end{vmatrix}}.}$

Расстояние между точками ${displaystyle mathbf {J} _{A}(A_{1},A_{2},A_{3},A_{4}),mathbf {J} _{B}(B_{1},B_{2},B_{3},B_{4})}$ :

Пусть ${displaystyle C_{1}={frac {A_{1}}{A_{1}+A_{2}+A_{3}+A_{4}}}-{frac {B_{1}}{B_{1}+B_{2}+B_{3}+B_{4}}};C_{2}={frac {A_{2}}{A_{1}+A_{2}+A_{3}+A_{4}}}-{frac {B_{2}}{B_{1}+B_{2}+B_{3}+B_{4}}}}$ и так далее.

Тогда расстояние между двумя точками: ${displaystyle d^{2}=-(C_{1}C_{2}alpha _{1,2}^{2}+C_{1}C_{3}alpha _{1,3}^{2}+C_{1}C_{4}alpha _{1,4}^{2}+C_{2}C_{3}alpha _{2,3}^{2}+C_{2}C_{4}alpha _{2,4}^{2}+C_{3}C_{4}alpha _{3,4}^{2}).}$

Сравнение формул треугольника и тетраэдра[править | править код]

Площадь(Объём)
${displaystyle S={sqrt {-{frac {1}{16}}{begin{vmatrix}0&1&1&1\1&0&a^{2}&b^{2}\1&a^{2}&0&c^{2}\1&b^{2}&c^{2}&0\end{vmatrix}}}}}$	${displaystyle V={sqrt {{frac {1}{288}}{begin{vmatrix}0&1&1&1&1\1&0&alpha _{2,1}^{2}&alpha _{3,1}^{2}&alpha _{4,1}^{2}\1&alpha _{2,1}^{2}&0&alpha _{3,2}^{2}&alpha _{4,2}^{2}\1&alpha _{3,1}^{2}&alpha _{3,2}^{2}&0&alpha _{4,3}^{2}\1&alpha _{4,1}^{2}&alpha _{4,2}^{2}&alpha _{4,3}^{2}&0\end{vmatrix}}}}}$ , где ${displaystyle alpha _{1,2}}$ — расстояние между вершинами 1 и 2
${displaystyle S={frac {1}{2}}ah_{a}}$	${displaystyle V={frac {1}{3}}S_{1}H_{1}}$
${displaystyle S={frac {1}{2}}absin gamma }$	${displaystyle V={frac {2}{3}}{frac {S_{1}S_{2}}{alpha _{3,4}}}sin(phi _{1,2})}$ , где ${displaystyle phi _{1,2}}$ — угол между гранями 1 и 2, ${displaystyle S_{1}}$ и ${displaystyle S_{2}}$ — площади граней, противолежащие вершинам 1 и 2
Длина(площадь) биссектрисы
$l_{c}={frac {2abcos {frac {gamma }{2}}}{a+b}}$	${displaystyle L_{1,2}={frac {2S_{1}S_{2}cos({frac {phi _{1,2}}{2}})}{S_{1}+S_{2}}}}$
Длина медианы
$m_{c}={frac {{sqrt {2a^{2}+2b^{2}-c^{2}}}}{2}}$	${displaystyle m_{1}={frac {sqrt {3(alpha _{1,2}^{2}+alpha _{1,3}^{2}+alpha _{1,4}^{2})-(alpha _{2,3}^{2}+alpha _{2,4}^{2}+alpha _{3,4}^{2})}}{3}}}$
Радиус вписанной окружности(сферы)
${displaystyle r={frac {2S}{a+b+c}}}$	${displaystyle r={frac {3V}{S_{1}+S_{2}+S_{3}+S_{4}}}}$
Радиус описанной окружности(сферы)
$R={frac {abc}{4S}}$	${displaystyle R={frac {S_{T}}{6V}}}$ , где ${displaystyle S_{T}}$ — площадь треугольника со сторонами ${displaystyle alpha _{1,2}alpha _{3,4},alpha _{1,3}alpha _{2,4},alpha _{1,4}alpha _{2,3}}$
Теорема косинусов
$cos {alpha }={frac {b^{2}+c^{2}-a^{2}}{2bc}}$	${displaystyle cos(phi _{1,2})={frac {A_{1,2}}{16S_{1}S_{2}}}}$ , где ${displaystyle phi _{1,2}}$ — угол между гранями 1 и 2, ${displaystyle S_{1}}$ и ${displaystyle S_{2}}$ — площади граней, противолежащие вершинам 1 и 2, ${displaystyle A_{1,2}}$ — алгебраическое дополнение элемента ${displaystyle alpha _{2,1}^{2}}$ матрицы ${displaystyle {begin{pmatrix}0&1&1&1&1\1&0&alpha _{2,1}^{2}&alpha _{3,1}^{2}&alpha _{4,1}^{2}\1&alpha _{2,1}^{2}&0&alpha _{3,2}^{2}&alpha _{4,2}^{2}\1&alpha _{3,1}^{2}&alpha _{3,2}^{2}&0&alpha _{4,3}^{2}\1&alpha _{4,1}^{2}&alpha _{4,2}^{2}&alpha _{4,3}^{2}&0\end{pmatrix}}}$
Теорема синусов
${frac {a}{sin alpha }}={frac {b}{sin beta }}={frac {c}{sin gamma }}$	${displaystyle {frac {S_{1}}{Psi _{1}}}={frac {S_{2}}{Psi _{2}}}={frac {S_{3}}{Psi _{3}}}={frac {S_{4}}{Psi _{4}}}}$ , где ${displaystyle S_{1},S_{2},S_{3},S_{4}}$ — площади граней, противолежащие вершинам 1, 2, 3, 4, ${displaystyle Psi ={sqrt {begin{vmatrix}1&-cos(A)&-cos(B)\-cos(A)&1&-cos(C)\-cos(B)&-cos(C)&1\end{vmatrix}}}}$ , где — двугранные углы вершины.
Теорема о сумме углов треугольника(соотношение между двугранными углами тетраэдра)
$alpha +beta +gamma =180^{circ }$	${displaystyle {begin{vmatrix}1&-cos left(phi _{2,1}right)&-cos left(phi _{3,1}right)&-cos left(phi _{4,1}right)\-cos left(phi _{2,1}right)&1&-cos left(phi _{3,2}right)&-cos left(phi _{4,2}right)\-cos left(phi _{3,1}right)&-cos left(phi _{3,2}right)&1&-cos left(phi _{4,3}right)\-cos left(phi _{4,1}right)&-cos left(phi _{4,2}right)&-cos left(phi _{4,3}right)&1\end{vmatrix}}=0}$ , где ${displaystyle phi _{1,2}}$ — угол между гранями 1 и 2
Расстояние между центрами вписанной и описанной окружностей (сфер)
${displaystyle R^{2}-d^{2}=2Rr}$	${displaystyle R^{2}-d^{2}={frac {S_{1}S_{2}alpha _{1,2}^{2}+S_{1}S_{3}alpha _{1,3}^{2}+S_{1}S_{4}alpha _{1,4}^{2}+S_{2}S_{3}alpha _{2,3}^{2}+S_{2}S_{4}alpha _{2,4}^{2}+S_{3}S_{4}alpha _{3,4}^{2}}{(S_{1}+S_{2}+S_{3}+S_{4})^{2}}}}$ , где ${displaystyle S_{1},S_{2},S_{3},S_{4}}$ — площади граней, противолежащие вершинам 1, 2, 3, 4. Другая запись выражения: ${displaystyle R^{2}-d^{2}=2rT,}$ где — расстояние между центром описанной сферы и центром сферы, проходящая через три вершины и инцентр.

Тетраэдр в неевклидовых пространствах[править | править код]

Объём неевклидовых тетраэдров[править | править код]

Существует множество формул нахождения объёма неевклидовых тетраэдров. Например, формула Деревнина — Медных^[7] для гиперболического тетраэдра и формула Дж. Мураками^[8] для сферического тетраэдра. Объём тетраэдра в сферическом пространстве и в пространстве Лобачевского, как правило, не выражается через элементарные функции.

Соотношение между двугранными углами тетраэдра[править | править код]

— для сферического тетраэдра.

— для гиперболического тетраэдра.

Где ${displaystyle Psi ={begin{pmatrix}1&-cos(A_{2,1})&-cos(A_{3,1})&-cos(A_{4,1})\-cos(A_{2,1})&1&-cos(A_{3,2})&-cos(A_{4,2})\-cos(A_{3,1})&-cos(A_{3,2})&1&-cos(A_{4,3})\-cos(A_{4,1})&-cos(A_{4,2})&-cos(A_{4,3})&1\end{pmatrix}}}$ — матрица Грама для двугранных углов сферического и гиперболического тетраэдра.

$A_{{i,j}}$ — угол между гранями, противолежащими i и j вершине.

Теорема косинусов[править | править код]

${displaystyle cos(A_{i,j})=-{frac {Phi _{i,j}}{sqrt {Phi _{i,i}Phi _{j,j}}}}}$ — для сферического и гиперболического тетраэдра.

${displaystyle cos(alpha _{i,j})={frac {Psi _{i,j}}{sqrt {Psi _{i,i}Psi _{j,j}}}}}$ — для сферического тетраэдра.

${displaystyle operatorname {ch} (alpha _{i,j})={frac {Psi _{i,j}}{sqrt {Psi _{i,i}Psi _{j,j}}}}}$ — для гиперболического тетраэдра.

Где
${displaystyle Phi ={begin{pmatrix}1&cos(alpha _{2,1})&cos(alpha _{3,1})&cos(alpha _{4,1})\cos(alpha _{2,1})&1&cos(alpha _{3,2})&cos(alpha _{4,2})\cos(alpha _{3,1})&cos(alpha _{3,2})&1&cos(alpha _{4,3})\cos(alpha _{4,1})&cos(alpha _{4,2})&cos(alpha _{4,3})&1\end{pmatrix}}}$ — матрица Грама для приведённых рёбер сферического тетраэдра.

${displaystyle Phi ={begin{pmatrix}1&operatorname {ch} (alpha _{2,1})&operatorname {ch} (alpha _{3,1})&operatorname {ch} (alpha _{4,1})\operatorname {ch} (alpha _{2,1})&1&operatorname {ch} (alpha _{3,2})&operatorname {ch} (alpha _{4,2})\operatorname {ch} (alpha _{3,1})&operatorname {ch} (alpha _{3,2})&1&operatorname {ch} (alpha _{4,3})\operatorname {ch} (alpha _{4,1})&operatorname {ch} (alpha _{4,2})&operatorname {ch} (alpha _{4,3})&1\end{pmatrix}}}$ — матрица Грама для приведённых рёбер гиперболического тетраэдра.

${displaystyle alpha _{i,j}}$ — приведенное расстояние между i и j вершин.

${displaystyle Psi _{i,j}}$ — алгебраическое дополнение матрицы Psi .

Теорема синусов[править | править код]

${displaystyle {frac {Phi _{1,1}}{Psi _{1,1}}}={frac {Phi _{2,2}}{Psi _{2,2}}}={frac {Phi _{3,3}}{Psi _{3,3}}}={frac {Phi _{4,4}}{Psi _{4,4}}}}$ — для сферического и гиперболического тетраэдра.

Радиус описанной сферы[править | править код]

${displaystyle {begin{vmatrix}1&cos(alpha _{2,1})&cos(alpha _{3,1})&cos(alpha _{4,1})&1\cos(alpha _{2,1})&1&cos(alpha _{3,2})&cos(alpha _{4,2})&1\cos(alpha _{3,1})&cos(alpha _{3,2})&1&cos(alpha _{4,3})&1\cos(alpha _{4,1})&cos(alpha _{4,2})&cos(alpha _{4,3})&1&1\1&1&1&1&{frac {1}{cos ^{2}(R)}}\end{vmatrix}}=0}$ — для сферического тетраэдра.

Другая запись выражения: ${displaystyle {frac {1}{cos(R)}}={frac {|{sqrt {Phi _{1,1}}}{overrightarrow {n_{1}}}+{sqrt {Phi _{2,2}}}{overrightarrow {n_{2}}}+{sqrt {Phi _{3,3}}}{overrightarrow {n_{3}}}+{sqrt {Phi _{4,4}}}{overrightarrow {n_{4}}}|}{sqrt {operatorname {det} Phi }}}}$ , где ${displaystyle {overrightarrow {n_{1}}},{overrightarrow {n_{2}}},{overrightarrow {n_{3}}},{overrightarrow {n_{4}}}}$ нормали граней тетраэдра.

Или с координатами вершин тетраэдра: ${displaystyle {frac {1}{cos(R)}}={frac {|{begin{vmatrix}0&{overrightarrow {i_{1}}}&{overrightarrow {i_{2}}}&{overrightarrow {i_{3}}}&{overrightarrow {i_{4}}}\1&X_{1}&Y_{1}&Z_{1}&T_{1}\1&X_{2}&Y_{2}&Z_{2}&T_{2}\1&X_{3}&Y_{3}&Z_{3}&T_{3}\1&X_{4}&Y_{4}&Z_{4}&T_{4}\end{vmatrix}}|}{sqrt {operatorname {det} Phi }}}}$ .

${displaystyle {begin{vmatrix}1&operatorname {ch} (alpha _{2,1})&operatorname {ch} (alpha _{3,1})&operatorname {ch} (alpha _{4,1})&1\operatorname {ch} (alpha _{2,1})&1&operatorname {ch} (alpha _{3,2})&operatorname {ch} (alpha _{4,2})&1\operatorname {ch} (alpha _{3,1})&operatorname {ch} (alpha _{3,2})&1&operatorname {ch} (alpha _{4,3})&1\operatorname {ch} (alpha _{4,1})&operatorname {ch} (alpha _{4,2})&operatorname {ch} (alpha _{4,3})&1&1\1&1&1&1&{frac {1}{operatorname {ch} ^{2}(R)}}\end{vmatrix}}=0}$ — для гиперболического тетраэдра.

Радиус вписанной сферы[править | править код]

${displaystyle {frac {1}{sin ^{2}(r)}}={frac {Phi _{1,1}+Phi _{2,2}+Phi _{3,3}+Phi _{4,4}+2{sqrt {Phi _{1,1}Phi _{2,2}}}cos(alpha _{1,2})+2{sqrt {Phi _{1,1}Phi _{3,3}}}cos(alpha _{1,3})+2{sqrt {Phi _{1,1}Phi _{4,4}}}cos(alpha _{1,4})+2{sqrt {Phi _{2,2}Phi _{3,3}}}cos(alpha _{2,3})+2{sqrt {Phi _{2,2}Phi _{4,4}}}cos(alpha _{2,4})+2{sqrt {Phi _{3,3}Phi _{4,4}}}cos(alpha _{3,4})}{operatorname {det} Phi }}}$ — для сферического тетраэдра.

Другая запись выражения: ${displaystyle {frac {1}{sin(r)}}={frac {|{sqrt {Phi _{1,1}}}{overrightarrow {r_{1}}}+{sqrt {Phi _{2,2}}}{overrightarrow {r_{2}}}+{sqrt {Phi _{3,3}}}{overrightarrow {r_{3}}}+{sqrt {Phi _{4,4}}}{overrightarrow {r_{4}}}|}{sqrt {operatorname {det} Phi }}}}$ , где ${displaystyle {overrightarrow {r_{1}}},{overrightarrow {r_{2}}},{overrightarrow {r_{3}}},{overrightarrow {r_{4}}}}$ единичные радиус векторы вершин тетраэдра.

${displaystyle {frac {1}{operatorname {sh} ^{2}(r)}}=-{frac {Phi _{1,1}+Phi _{2,2}+Phi _{3,3}+Phi _{4,4}+2{sqrt {Phi _{1,1}Phi _{2,2}}}operatorname {ch} (alpha _{1,2})+2{sqrt {Phi _{1,1}Phi _{3,3}}}operatorname {ch} (alpha _{1,3})+2{sqrt {Phi _{1,1}Phi _{4,4}}}operatorname {ch} (alpha _{1,4})+2{sqrt {Phi _{2,2}Phi _{3,3}}}operatorname {ch} (alpha _{2,3})+2{sqrt {Phi _{2,2}Phi _{4,4}}}operatorname {ch} (alpha _{2,4})+2{sqrt {Phi _{3,3}Phi _{4,4}}}operatorname {ch} (alpha _{3,4})}{operatorname {det} Phi }}}$ — для гиперболического тетраэдра.

Расстояние между центрами вписанной и описанной сфер[править | править код]

${displaystyle {frac {cos(d)}{sin(r)cos(R)}}={frac {{sqrt {Phi _{1,1}}}+{sqrt {Phi _{2,2}}}+{sqrt {Phi _{3,3}}}+{sqrt {Phi _{4,4}}}}{sqrt {operatorname {det} Phi }}}}$ — для сферического тетраэдра.

Формулы тетраэдра в барицентрических координатах[править | править код]

Координаты центра вписанной сферы:

${displaystyle mathbf {J} _{r}({sqrt {Phi _{1,1}}},{sqrt {Phi _{2,2}}},{sqrt {Phi _{3,3}}},{sqrt {Phi _{4,4}}}).}$ — для сферического тетраэдра.

Координаты центра описанной сферы:

${displaystyle mathbf {J} _{R}={begin{vmatrix}0&mathbf {J_{1}} &mathbf {J_{2}} &mathbf {J_{3}} &mathbf {J_{4}} \1&1&cos(alpha _{1,2})&cos(alpha _{1,3})&cos(alpha _{1,4})\1&cos(alpha _{2,1})&1&cos(alpha _{2,3})&cos(alpha _{2,4})\1&cos(alpha _{3,1})&cos(alpha _{3,2})&1&cos(alpha _{3,4})\1&cos(alpha _{4,1})&cos(alpha _{4,2})&cos(alpha _{4,3})&1\end{vmatrix}}.}$ — для сферического тетраэдра.

Тетраэдры в микромире[править | править код]

Правильный тетраэдр образуется при sp³-гибридизации атомных орбиталей (их оси направлены в вершины правильного тетраэдра, а ядро центрального атома расположено в центре описанной сферы правильного тетраэдра), поэтому немало молекул, в которых такая гибридизация центрального атома имеет место, имеют вид этого многогранника.
Молекула метана СН₄.
Ион аммония NH₄⁺.
Сульфат-ион SO₄^2-, фосфат-ион PO₄^3-, перхлорат-ион ClO₄^– и многие другие ионы.
Алмаз C — тетраэдр с ребром, равным 2,5220 ангстрем.
Флюорит CaF₂, тетраэдр с ребром, равным 3,8626 ангстрем.
Сфалерит, ZnS, тетраэдр с ребром, равным 3,823 ангстрем.
Оксид цинка, ZnO.
Комплексные ионы [BF₄] ^–, [ZnCl₄]^2-, [Hg(CN)₄]^2-, [Zn(NH3)₄]²⁺.
Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO₄]^4-.

Тетраэдры в живой природе[править | править код]

Тетраэдр из грецких орехов

Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.

Тетраэдры в технике[править | править код]

Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм,Стержни испытывают только продольные нагрузки.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр^[9].

Тетраэдры в философии[править | править код]

«Платон говорил, что наименьшие частицы огня суть тетраэдры»^[10].

См. также[править | править код]

Симплекс — n-мерный тетраэдр
Тетраэдр Мейсснера
Тетраэдр Рёло
Треугольник

Примечания[править | править код]

↑ Древнегреческо-русский словарь Дворецкого «τετρά-εδρον». Дата обращения: 20 февраля 2020. Архивировано из оригинала 28 декабря 2014 года.
↑ Селиванов Д. Ф.,. Тело геометрическое // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с. Архивная копия от 10 января 2014 на Wayback Machine
↑ В. Э. МАТИЗЕН Равногранные и каркасные тетраэдры «Квант» № 7, 1983 г.
↑ Моденов П.С. Задачи по геометрии. — М.: Наука, 1979. — С. 16.
↑ Маркелов С. Формула для объема тетраэдра// Математическое просвещение. Вып. 6. 2002. С. 132
↑ Источник. Дата обращения: 31 марта 2018. Архивировано 30 августа 2017 года.
↑ Источник. Дата обращения: 31 марта 2018. Архивировано 31 марта 2018 года.
↑ http://knol.google.com/k/триггер#view Архивная копия от 23 ноября 2010 на Wayback Machine Триггер
↑ Вернер Гейзенберг. У истоков квантовой теории. М. 2004 г. стр.107

Литература[править | править код]

Матизен В. Э., Дубровский. Из геометрии тетраэдра «Квант», № 9, 1988 г. С.66.
Заславский А. А. Сравнительная геометрия треугольника и тетраэдра // Математическое просвещение, сер. 3 (2004), № 8, стр. 78-92.
Понарин Я. П. Элементарная геометрия. Том 3. Треугольники и тетраэдры.2009 г.

Источник

Определение тетраэдра

Виды тетраэдра

Формулы площади и объема правильного тетраэдра

Тетраэдр,

Что же такое этот «тетраэдр»?

На самом деле, тетраэдры нас повсюду окружают

Основные виды тетраэдров

Основные формулы тетраэдра

Основные формулы тетраэдра (продолжение)

Что такое тетраэдр: определение, виды, формулы площади и объема

Определение тетраэдра

Тетраэдр

Математические характеристики тетраэдра

Вариант развертки

Видео. Тетраэдр из набора “Волшебные грани”

Видео. Вращение всех правильных многогранников

Популярное

Тетраэдр.

Свойства тетраэдра.

Типы тетраэдров.

Формулы для определения элементов тетраэдра.

Площадь пирамиды

Полная площадь поверхности пирамиды через высоту и сторону основания

Полная площадь тетраэдра

Боковая поверхность пирамиды через периметр и апофему

Боковая поверхность пирамиды через высоту и сторону основания

Свойства[править | править код]

Типы тетраэдров[править | править код]

Равногранный тетраэдр[править | править код]

Ортоцентрический тетраэдр[править | править код]

Прямоугольный тетраэдр[править | править код]

Каркасный тетраэдр[править | править код]

Соразмерный тетраэдр[править | править код]

Инцентрический тетраэдр[править | править код]

Правильный тетраэдр[править | править код]

Объём тетраэдра[править | править код]

Замечание[править | править код]

Формулы тетраэдра в декартовых координатах в пространстве[править | править код]

Формулы тетраэдра в барицентрических координатах[править | править код]

Сравнение формул треугольника и тетраэдра[править | править код]

Тетраэдр в неевклидовых пространствах[править | править код]

Объём неевклидовых тетраэдров[править | править код]

Соотношение между двугранными углами тетраэдра[править | править код]

Теорема косинусов[править | править код]

Теорема синусов[править | править код]

Радиус описанной сферы[править | править код]

Радиус вписанной сферы[править | править код]

Расстояние между центрами вписанной и описанной сфер[править | править код]

Формулы тетраэдра в барицентрических координатах[править | править код]

Тетраэдры в микромире[править | править код]

Тетраэдры в живой природе[править | править код]

Тетраэдры в технике[править | править код]

Тетраэдры в философии[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти плошадь осевого сечения конуса

Как найти работу совершенную тепловым двигателем

Как найти причину падения

Добавить комментарий Отменить ответ