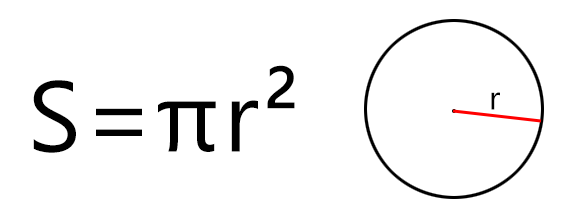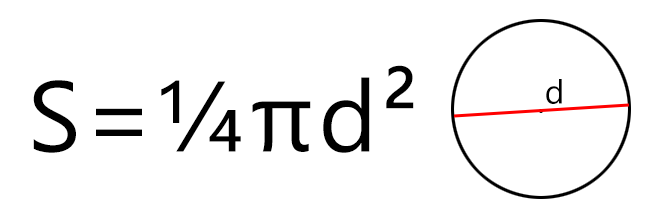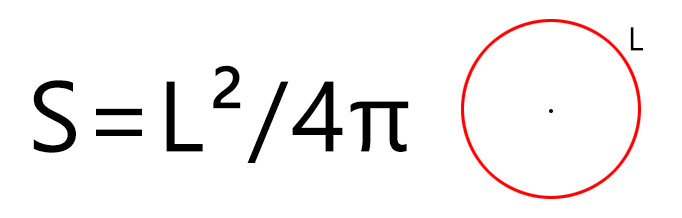Калькулятор площади окружности (круга) через длину (периметр)
При помощи данного калькулятора можно вычислить площадь окружности зная ее длину (периметр).
Длина окружности P
Формула для вычисления площади окружность выглядит следующим образом:
S = πR2 при вычислении через радиус
S = πD2/4 при вычислении через диаметр
Таким образом для нахождения окружности нам необходимо знать либо ее диаметр D, либо радиус R.
Зная длину (периметр) окружности проще всего установить диаметр, т.к. диаметр окружности в π раз меньше ее длины. Соответственно для установления диаметра окружности необходимо ее длину разделить на π.
D = P/π
Найдя диаметр окружности, мы можем узнать площадь круга через формулу, указанную выше:
S = πD2/4
В рассмотренном случае, мы для нахождения площади круга, использовали две формулы. Но как же нам найти площадь используя только одну формулу? Давайте постараемся создать ее сами.
В формулу S = πD2/4 вместо D подставим значение P/π соответственно получаем
S = (π/4)*(P/π)2 = (π*P2)/(π2*4) = (π*P2)/(π*π*4) = P2/(π*4)
или
S = P2/(π*4)
Где:
S – площадь окружности.
P – длина окружности.
D – диаметр окружности
π – математическая постоянная, константа, которая примерно равна 3.14
Пример решения
P = 12.5
Первым действием мы вычисляем диаметр окружности.
D = 12.5/π = 3.9788735772973833
Затем, зная, что диаметр окружности равен 3.9788735772973833 вычисляем ее площадь
S = π*3.97887357729738332/4 = 12.434
Для вычисления площади круга через его длину в одно действие нам необходимо воспользоваться следующей формулой – S = P2/(π*4)
Подставляем в данную формулу известное нам значение – длину круга
S = 12.52/(π*4) = 12.434
Распишем подробнее
S = 12.52/(π*4) = 156.25/12.566371 = 12.434
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
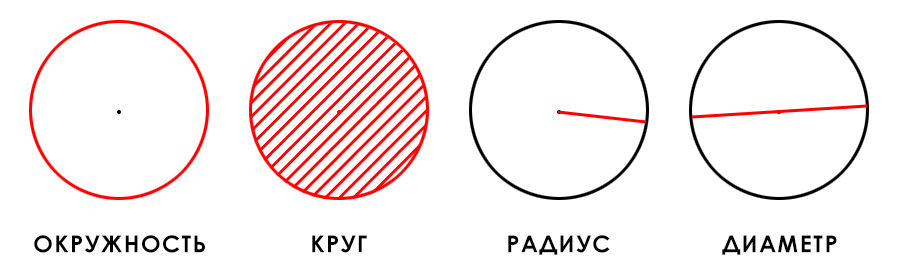
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
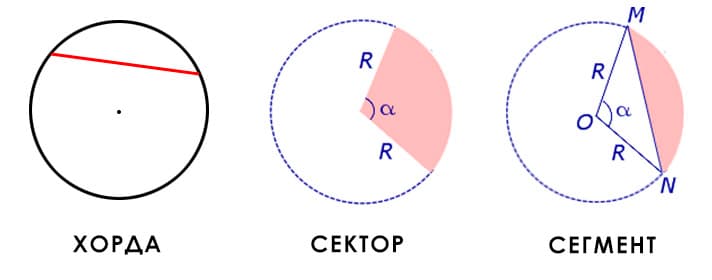
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
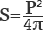
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Определение: Круг- это часть плоскости , ограниченная окружностью, круг является выпуклой фигурой.

Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Нужно быстро определить площадь круга, если известен периметр, радиус или длина? Тогда воспользуйтесь этим простым онлайн-калькулятором. Заполните одну любую ячейку в калькуляторе окружности и нажмите на кнопку расчета. Остальные величины посчитаются автоматически. Также напротив значений будут выведены формулы вычислений.
После того как будет найден радиус окружности, можно воспользоваться двумя нижерасположенными калькуляторами и найти величины сегмента и сектора круга.
Обратите внимание! Если у сегмента известны только площадь или периметр, то произвести вычисления не получится. Для расчета остальных значений сегмента, помимо его площади и периметра также должны быть известны длина хорды, длина дуги или высота.
Калькулятор окружности:
Достаточно заполнить только одну ячейку — остальное калькулятор посчитает сам.
Периметр или длина окружности (P)
Калькулятор сектора окружности:
Достаточно ввести только одно значение и указать радиус окружности — остальное калькулятор посчитает сам.
Центральный угол сектора в градусах (α)
Площадь сектора окружности (S1)
Калькулятор сегмента окружности:
Достаточно ввести только одно* значение и указать радиус окружности — остальное калькулятор посчитает сам.
Исключения:
* – при известном периметре (P2) нужно дополнительно указать длину дуги (l1) или хорды (c).
* – при известной площади (S2) нужно дополнительно указать длину хорды (c) или высоты (h).
Угол сегмента в градусах (α1)
Площадь сегмента окружности (S2)
Округление:
* – обязательно заполнить
|
Например, нужно вычислить площадь круглой колонны. Диаметр не измеришь. Какие формулы использовать, чтобы высчитать её площадь. Формула площади: S = П*r²Формула длины окружности (периметра): P = 2*П*rП – это число Пи: 3.14…Из окружности находим радиус: r = P/2ПИ подставляем это в формулу площади: S = П*(P/2П)² = П*P²/4П²Если я правильно раскрыл скобки со степенями, то: П – сокращаются и остаётся: S = P²/4Павтор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Для того, чтобы найти площадь круга через длину окружности, нужно сначала вспомнить формулы, по которым вычисляется: 1) Длина окружности. 2) Площадь круга. Итак, формула для длины окружности: l =2πR. Что касается площади круга, то она вычисляется по формуле: C = πR². Здесь R – это радиус, а π – число Пи, которое равно 3,14. Если известна длина окружности, то легко выразить её радиус. После этого остаётся лишь подставить полученное значение в формулу для площади круга. R = l / 2π. C = π * (l / 2π)² = l² / 4π. Пример Дана длина окружности l = 20 см. Нужно найти площадь круга. C = l² / 4π = (20 * 20) / (4 * 3,14) = 400 / 12,56 = 31,85 см. Таким образом, если длина окружности равна 20 см., то площадь круга будет составлять 31,85 см. Урания 2 года назад Площадь круга можно легко рассчитать по известной формуле, в которую входит радиус круга (или окружности, что одно и то же): S = πR²; Где R – это радиус окружности, а число π – это неизменяемая величина, равная – 3,14 В свою очередь, длина окружности тоже рассчитывается через его радиус: С = 2πR; Отсюда следует, что выразив радиус окружности из последней формулы (R = C/2π) , и подставив его в первую формулу, мы получим формулу, в которой площадь круга будет выражена через его длину окружности: S = π(C/ 2π)². После возведения в квадрат и необходимых сокращений, получим окончательную искомую формулу: S = C²/4π Эта именно та формула, в которой площадь (S) круга выражена через его длину окружности (С). Чёрная Луна 4 года назад Выедим формулу для нахождения площади круга, при условии использования длинны окружности. Как известно, формула площади круга: S = 2πR²; Формула периметра окружности или длинны окружности вычисляется по формуле: С = 2πR; R – это радиус окружности, число π – всегда равно 3,14. Радиус необходим нам для того, чтобы найти площадь. А зная длину окружности мы можем вычислить радиус. R = C/2π Заменяем эту форму на радиус в формуле по нахождению площади окружности: S = 2π(C/2π)²; После раскрытия скобок и сокращения получаем следующую формулу: S = C²/4π По конечной формуле можно найти площадь круга, зная его периметр. Для этого есть формула вычисления площади окружности – где S – искомая площадь, C – длина окружности, П – число равное 3,14. Допустим длина окружности равна 75 сантиметрам. Возводим ее в квадрат, получаем 5625. Теперь получаем 5625/4П. Сокращаем выражение до минимума – 5625/4=1406 Теперь это значение выглядит как 1406/п = 447 квадратных сантиметров. Это стандартная геометрическая задача. Радиус колонны вычисляется из формулы длины окружности L = 2 * пи * R, откуда R = 0.5 * L / пи Площадь находим по формуле S = пи * R^2 = пи * (0.5 * L / пи)^2 = 0.25 * пи * L^2. Аналогично можно посчитать и объем колонны, зная лишь длину окружности и высоту. V = 0.25 * пи * L^2 * H, где H – высота колонны. -Irinka- 4 года назад Выведенная формула для нахождения S окружности, зная длину его окружности: Так как площадь круга равняется Подставляя в формулу значение радиуса, мы получаем формулу нахождения площади круга, через длину окружности. Допустим длина l=8 см, число π=3,14 Получается, что площадь круга будет равна 5 см². Бекки Шарп 3 года назад Есть такая всем известная константа Пи (3,1425), она равна длине окружности поделенной на длину диаметра. То есть зная длину, мы всегда найдем диаметр. А зная диаметр мы можем посчитать площадь круга по известной формуле. Знаете ответ? |