Как найти площадь окружности по клеткам 1х1

Площадь круга равна произведению числа на квадрат радиуса:

Задача 1. Найдите площадь круга, считая стороны клеток равными 1 (см. рис. 1). В ответе укажите .

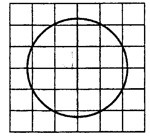
Рис.1

Решение.
Площадь круга равна произведению числа на квадрат радиуса. Найдём радиус. Из центра проведём радиус . В треугольнике сторона — гипотенуза, катеты равны 1 и 2 (см. рис. 2).

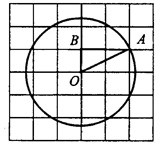
Рис.2

Найдём гипотенузу по теореме Пифагора.
Площадь круга
Ответ: 5.
Задача 2. На клетчатой бумаге нарисовано два круга (см. рис. 3). Площадь внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.

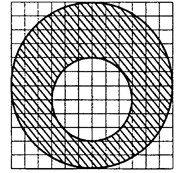
Рис.3

Решение.
Радиус внутреннего круга — 3 клетки, его площадь равна . Радиус внешнего круга — 6 клеток, то есть , поэтому его площадь равна Площадь заштрихованной фигуры равна разности 12 — 3 = 9.
Ответ: 9.
Площадь сектора с углом градусов равна
Задача 3. Найдите площадь сектора с углом 18 градусов и радиусом 4. В ответе укажите .
Решение.
Посчитаем площадь сектора по формуле
Ответ: 0,8.
Задача 4. Найдите площадь заштрихованного сектора, считая стороны клеток равными 1 (см. рис. 4). В ответе укажите .

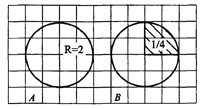
Рис.4

Решение.
На рисунке 4A) площадь круга с радиусом = 2 равна
На рисунке 4В) площадь сектора составляет от площади круга (если круг разделить на 4 равные части, то одна из них как раз и будет равна заданному сектору), то есть

Можно было решать задачу по-другому. Площадь сектора равна площади круга, делённой на 4.

Ответ: 1.
Задача 5. Найдите площадь заштрихованных секторов на рисунках C и D, считая стороны клеток равными 1 (см. рис. 5).

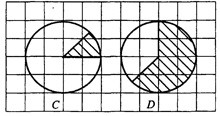
Рис.5

В ответе укажите .
Решение. Посчитаем, какая часть круга закрашена. Проведя дополнительные линии (см. рис. 6), видим, что сектор на рисунке 6C) составляет – часть круга, а сектор на рисунке 6D) составляет
частей круга (круг разделён на 8 равных частей, и закрашено 5 таких частей).
Находим площади секторов на рисунках 6C) и 6D).

Рис.6

1-й способ.
Поделим площадь круга на 8, получим площадь сектора на рисунке 6C), потом умножим эту площадь на 5, получим площадь сектора на рисунке 6D).

Ответ: 0,5 и 2,5.
2-й способ. Найдём площадь круга.

Ответ: 0,5 и 2,5.

На клетчатой бумаге нарисованы два круга

Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.

Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):

Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:

Разделим результат на число Пи и запишем ответ.

На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.

Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:

Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:

Получили, что его площадь в 4 раза больше.

Следовательно, она равна 51∙4 = 204 см 2

Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см 2 .

*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.

Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).

Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:

Выразим площадь большего круга, так как его радиус равен 6х:

Как видно, площадь большего круга в 4 раза больше.

Следовательно, она равна 1∙4 = 4 см 2

Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см 2 .

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Обозначим размер клетки переменной х (икс).

Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3 ∙ х, то

Выразим площадь большего круга. Так как его радиус равен 4 ∙ х, то

Разделим площадь большего на площадь меньшего:

То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:

Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см 2 .

Вычислим радиус меньшего круга. Его площадь равна 9, значит,

Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:

Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:

Определяем площадь большего круга:

Находим разность: 16 – 9 = 7 см 2

На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.

В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.

На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?

По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна 32∙3 = 96.

Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/л.

В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.

В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.

Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.

На этом всё. Успеха вам!

С уважением, автор проекта Александр Крутицких.

Как найти площадь окружности по клеткам

На клетчатой бумаге с размером клетки 1 × 1 изображён вписанный в окружность угол ABC. Найдите его градусную величину.

Аналоги к заданию № 27890: 26237 27891 509571 Все

На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

Отрежем от закрашенной фигуры сектор, отмеченный синим цветом, и добавим к ней сектор, выделенный красным цветом. Указанные секторы равны, поэтому площадь фигуры не изменилась. Следовательно, она равна трём четвертям площади круга, радиус которого см. Поэтому

см 2 .

Хотелось бы более “научного” доказательства. Аргумент “это видно” не достаточен, так как всем видно разное. Спасибо!

На рисунке ВИДНО, что они равны. Или задайте прямые уравнениями и и найдите угол между ними. Но то, что уравнения именно такие, тоже ВИДНО по рисунку. Задания на работу с рисунками предполагают считывание информации с рисунка.

На клетчатой бумаге с размером клетки 1 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.

Треугольник прямоугольный, значит, радиус описанной вокруг него окружности равен половине гипотенузы.

Круг на клетчатой бумаге

Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.

Для решения обеих задач надо определить величину соответствующего ему центрального угла.

Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.

Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.

Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).

Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).

1) На клетчатой бумаге изображён круг площадью 60.

Найти площадь заштрихованного сектора.

Так как центральный угол, соответствующий данному сектору, равен 90º, то

2) На клетчатой бумаге изображён круг.

Какова площадь круга, если площадь заштрихованного сектора равна 17?

Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.

Следовательно, площадь сектора составляет 1/4 от площади круга: S_круга=S_{сектора}:(1/4)=17·4=68.

3) Найти площадь круга, если площадь заштрихованного сектора равна 21.

Площадь заштрихованного сектора составляет 3/4 площади круга.

Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).

Так как 45° составляет от 360° 1/8 часть, то

5) На клетчатой бумаге изображен круг площадью 96.

Найдите площадь заштрихованного сектора.

Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.

S_{закрашенного сектора}=S_{незакрашенного сектора}-S_круга=96-12=84.

А как определить на клетчатой бумаге центральные углы в 60° и 30°?

Можно рассуждать следующим образом.

Рассмотрим треугольник ABC.

Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.

Но AO=BO (как радиусы).

Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.

6) Найти площадь заштрихованного сектора, если площадь круга равна 30.

Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и S_{сектора}=S_круга:6=30:6=5.

7) Найти площадь круга, если площадь заштрихованного сектора равна 24.

Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.

8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.

Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.

Следовательно, на площадь закрашенной части приходится 5/6 круга:

В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.

9) Центральный угол равен 30+45=75°,

площадь заштрихованного сектора составляет

1/12+1/8=5/24 площади круга, то есть

10) Центральный угол равен 180-30=150°,

площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,

11) Центральный угол равен 60-45=15°,

площадь заштрихованного сектора составляет 1/24 площади круга

12) Центральный угол равен 15+90=105°

[spoiler title=”источники:”]

http://ege.sdamgia.ru/test?theme=123

[/spoiler]

   Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.

Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально  (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):

Найдите (в см²) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга: 

Значит,

Разделим результат на число Пи и запишем ответ.

Ответ: 3

На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.

Площадь заштрихованной фигуры можно найти вычислив разность между  площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:

Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:

Получили, что его площадь в 4 раза больше.

Следовательно, она равна    51∙4 = 204 см²

Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см². 

*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.

Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить  размер клетки переменной х (икс).

Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:

Выразим площадь большего круга, так как его радиус равен 6х:

Как видно, площадь большего круга в 4 раза больше.

Следовательно, она равна  1∙4 = 4 см²

Таким образом, площадь заштрихованной фигуры равна   4 – 1 = 3 см². 

Ответ: 3

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Обозначим размер клетки переменной х (икс).

Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3∙х, то

Выразим площадь большего круга. Так как его радиус равен 4∙х, то

Разделим площадь большего на площадь меньшего:

То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:

Таким образом, площадь заштрихованной фигуры равна   16 – 9 = 7 см². 

*Второй способ.

Вычислим радиус меньшего круга. Его площадь равна 9, значит,

Найдём размер  клетки и затем сможем определить радиус большего круга. Размер клетки равен:

Так как радиус большего круга соответствует 4 клеткам, то его радиус  будет равен:

Определяем площадь большего круга:

Находим разность:    16 – 9 = 7 см²

Ответ: 7

На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.

В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.

Ответ: 24

На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?

По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна  32∙3 = 96.

Ответ: 96

Найдите (в см²) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Посмотреть решение

Найдите площадь S круга, считая стороны квадратных клеток равными 1.  В ответе укажите S/л.

Посмотреть решение

Небольшой итог.

В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.

В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.

Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.

На этом всё. Успеха вам!

С уважением, автор проекта Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Задачи на клетчатой бумаге интересны тем, что можно их решать различными способами – и через дополнительное построение, и через различные геометрические формулы. Так как задач таких сейчас полно в сети, ещё раз обозначу себе картинкой условие:

У нас нет ничего в условии кроме длины клетки, равной 1/√π

Как найти площадь?

Например, по такой формуле, где альфа – размер угла.

Но у нас нет ни угла, ни радиуса.

Значит, находим радиус. На глаз тут 4,5 клетки, но мы будем точнее, если нарисуем вот такой треугольник прямоугольник, в котором радиус будет гипотенузой и через теорему Пифагора его найдём.

(4/√π)2 + (2/√π)2 = 16/π+4/π = √(20/π)

Как найти угол? Если разделить всю окружность на 4 части, то видно, что закрашенная часть составит целую четверть и ещё её половинку. То бишь, 1/4+0,5Х1/4 Это не что иное как 3/8

Теперь считаем угол: 360Х3/8=135 градусов.

Теперь, когда у нас есть все данные, подставляем в формулу.

S=135/360 Х π Х (√(20/π))2

Квадрат и корень квадратный сокращаются, получаем 135/360 Х π Х 20/π

Следом сокращается и п, остаётся 135/360 Х 20/1 = 135/18 = 7,5

Поскольку площадь измеряется в квадратных сантиметрах в нашей задаче, то и ответ будет 7,5 кв.см

Сайты, меню, вход, новости