Сегодня мы говорим про окружность и круг, друзья мои. У многих шестиклассников, да и не только у них, возникают трудности с этой темой. А она-то как раз и есть ваш реальный шанс на получение хорошей отметки. Да, есть там одна заковырка. Вот она не нравится ребятам. Но я сейчас подробно всё расскажу. Давайте приступим)))
Сначала дам несколько определений. Они очень лёгкие, просто посмотрите:
Есть окружность, а есть круг:
Определения, ребята, есть у вас в учебнике. Их надо знать наизусть, учителя это любят. Выучите их, пожалуйста. А я вам простыми словами расскажу, чтобы совсем понятно было.
- Окружность – это линия на бумаге или ещё где-нибудь. На асфальте мелом, например.
- Круг – это часть листа (плоскости).
Как отличить круг от окружности?
Круг я могу вырезать ножницами и у меня в руках будет круглый кусок бумаги. А линию я вам как вырежу?!
Окружность нельзя вырезать ножницами! Она же линия!
Дальше. У вас будут две формулы. Я знаю, что их три, на самом деле – две. Расскажу попозже. Сначала основные определения простыми словами дам:
А это диаметр. Присмотритесь: вам ничего не показалось?)))
Вы молодцы, если вам показалось, что один диаметр – это ДВА РАДИУСА! Так и есть!
Значит, вот эти две формулы одинаковые.
Запомните: один диаметр – это два радиуса! Один радиус – это половина диаметра! Если знаете диаметр – радиус тоже знаете!!! И наоборот!
Что такое C в этой формуле? Это длина окружности. Если я возьму окружность, мысленно её разрежу и разогну, то получится прямая. Тогда я смогу померить её длину. А можно и не разрезать. Возьмите сантиметровую ленту у бабушки или у мамы. Потом найдите чашку на кухне, отметьте точку (незаметно, чтобы потом смыть) и действуйте по схеме:
Есть ещё формула площади круга:
Тоже легко. В статье я уже не буду об этом писать. А вот видео, в нём я задачи разбираю для шестиклассников, именно на эту тему. Там про площадь круга рассказываю подробно. Для других классов тоже подойдёт, кто не понял, забыл или не успел)))
Подведём итог. Если вы будете знать наизусть определение диаметра и радиуса, если вы будете знать 2 формулы (а на самом деле одну!) длины окружности и одну формулу площади круга, то по этой теме у вас точно будет не ниже четвёрки, друзья мои школьники.
Если статья показалась вам полезной, поставьте, пожалуйста, оценку. Она поможет мне дальше помогать вам)))
Вот здесь кое-что про борьбу со списыванием с сайта ГДЗ
А вот здесь – как учить стихи
P. S.: Про число “ПИ” я ничего не говорила в этой статье. Но в видео я про него рассказываю. Это фантастическое, просто удивительное число!!!!! Но мне места не хватило, В другой раз…
Прежде чем определится, как рассчитать площадь круга,
необходимо хорошо
усвоить и понять в чём разница между окружностью и кругом. Что
называется окружностью, а что подразумевают под словом круг.
Важно!
Замкнутая кривая (линия),
чьи точки лежат на
одинаковом расстоянии от одной точки её центра, называется
окружностью.
Окружность разбивает плоскость на две области:
внутреннюю и внешнюю.
Важно!
Та часть плоскости, которая лежит
внутри окружности (вместе с самой окружностью)
называется кругом.
Другими словами, для простоты понимания, следует запомнить:
- окружность — это замкнутая линия (
граница круга). - круг — это внутренняя область окружности.
- У окружности нельзя посчитать площадь!
А у круга найти площадь,
зная формулу,
достаточно легко.
Как найти площадь круга
Запомните!
Для расчета площади круга используется формула:
- S = πR2,
где R — радиус круга, - S = π
()2 =
π
=π
, где
D — диаметр круга, т.к.
R =
Как решать задачи на площадь круга
Теперь, зная, по какой формуле считается площадь круга,
решим задачи на
площадь круга.
Зубарева 6 класс. Номер 675(г)
Условие задачи:
Найдите площадь круга, радиус которого равен 1,2 см.
Воспользуемся формулой площади круга:
S = πR2 =
3,14 · 1,22 = 3,14 · 1,44 = 4,5216 см2
Обратите внимание, что площадь измеряется в квадратных единицах.
Всегда проверяйте свои ответы, правильно ли вы указали единицы
измерения.
Зубарева 6 класс. Номер 677(б)
Условие задачи:
Определите радиус круга, площадь которого равна 1,1304 см2.
Выразим из формулы радиус:
S = πR2
R = √
S /
π
= √ 1,1304 /
3,14 = √ 0,36 =
0,6 см
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
Загрузить PDF
Загрузить PDF
Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала нужно запомнить формулу, по которой вычисляется площадь круга: 
. Формула проста: чтобы найти площадь круга, нужно знать только его радиус. Но нужно уметь преобразовывать другие исходные величины, чтобы воспользоваться этой формулой.
-
1
Найдите радиус круга. Радиус – это отрезок, соединяющий центр круга с любой точкой внешней окружности круга. Радиус можно измерить в любом направлении: он будет одним и тем же. Радиус также равен половине диаметра круга. Диаметр – это отрезок, который проходит через центр круга и соединяет две точки внешней окружности круга.[1]
- Как правило, значение радиуса дано в условиях задачи. Довольно трудно найти точный центр круга, если только он не обозначен на круге, который нарисован на бумаге.
- Например, радиус круга равен 6 см.
-
2
Возведите радиус в квадрат. Формула для вычисления площади круга:
, где – радиус, который возведен во вторую степень (в квадрат).[2]
-
3
Полученный результат умножьте на число Пи. Это число обозначается греческой буквой
и представляет собой математическую константу, которая характеризует взаимосвязь радиуса и площади круга. Число Пи приблизительно равно 3,14. Точное значение числа Пи включает бесконечное количество цифр. Иногда ответ (площадь круга) записывается с постоянной .[3]
- В нашем примере (r = 6 см) площадь вычисляется так:
-
4
Запишите ответ. Помните, что площадь измеряется в квадратных единицах. Если радиус дан в сантиметрах, площадь измеряется в квадратных сантиметрах. Если радиус дан в миллиметрах, площадь измеряется в квадратных миллиметрах. Уточните у преподавателя, нужно ли представить ответ с постоянной
или в числовой форме, используя приблизительное значение числа Пи. Если требование не ясно, запишите оба варианта ответа.[4]
- В нашем примере (r = 6 см) S = 36 см2 или S = 113,04 см2.
Реклама
- В нашем примере (r = 6 см) S = 36
-
1
Измерьте или запишите диаметр. В некоторых задачах радиус не дан. Вместо радиуса указывается диаметр. Если диаметр нарисован на бумаге, измерьте его с помощью линейки. Скорее всего, числовое значение диаметра будет задано.
- Например, диаметр круга равен 20 мм.
-
2
Разделите диаметр пополам. Помните, что диаметр равен удвоенному радиусу. Поэтому разделите любое значение диаметра на 2, чтобы найти радиус.
- Таким образом, если диаметр круга равен 20 мм, то радиус круга равен 20/2 = 10 мм.
-
3
-
4
Запишите ответ. Помните, что площадь измеряется в квадратных единицах. В нашем примере диаметр дан в миллиметрах, поэтому радиус тоже измеряется в миллиметрах, а площадь в квадратных миллиметрах. В нашем примере S =
мм2.
- Также ответ можно представить в численной форме, используя вместо приблизительное значение 3,14. В этом случае S = (100)(3,14) = 314 мм2.
Реклама
- Также ответ можно представить в численной форме, используя вместо
-
1
Запишите преобразованную формулу. Если известна длина окружности круга, можно воспользоваться преобразованной формулой для вычисления его площади. Такая формула включает длину окружности, а не радиус, и записывается так:
-
2
Измерьте или запишите длину окружности. В некоторых ситуациях нельзя точно измерить диаметр или радиус. Если диаметр не нарисован или центр не отмечен, очень сложно найти точный центр круга. Длину окружности некоторых предметов (например, сковороды) довольно легко измерить с помощью рулетки, то есть можно найти более точное значение длины окружности, чем диаметра.[5]
- Например, длина окружности круга (или круглого предмета) равна 42 см.
-
3
-
4
Запишите формулу для вычисления площади круга. Запишите преобразованную формулу на основе соотношения между длиной окружности и радиусом. Подставьте последнее равенство в стандартную формулу для вычисления площади круга:[7]
-
5
Воспользуйтесь преобразованной формулой, чтобы решить задачу. Теперь в формуле вместо радиуса присутствует длина окружности, поэтому можно вычислить площадь круга по известной длине окружности. Подставьте значение длины окружности и выполните вычисления следующим образом:[8]
-
6
Запишите ответ. Если длина окружности дана в виде числа, а не произведения числа и
, ответ можно записать с в знаменателе. Или вместо числа Пи подставьте его приблизительное значение (3,14).[9]
Реклама
-
1
Запишите известные величины. В некоторых задачах дана площадь сектора круга, по которой нужно найти площадь всего круга. Внимательно прочитайте такую задачу; ее условие может выглядеть так: «Площадь сектора круга равна 15
см2. Найдите площадь всего круга».[10]
-
2
Запомните определение сектора. Сектор круга – это часть круга, которая ограничена дугой и двумя радиусами. Пространство между такими радиусами и дугой называется сектором.[11]
-
3
Измерьте центральный угол сектора. Воспользуйтесь транспортиром, чтобы измерить угол между двумя радиусами. Линейку (прямолинейную шкалу) совместите с одним из радиусов, причем центр линейки должен совпадать с центром круга. Затем найдите величину угла; для этого посмотрите на точку пересечения второго радиуса с угломерной шкалой.[12]
- Не перепутайте внутренний и внешний угол между двумя радиусами. В задаче должно быть указано, с каким углом работать. Помните, что сумма внутреннего и внешнего углов равна 360 градусов.
- Во многих задачах центральный угол дан, то есть измерять его не нужно. Например, в задаче может быть сказано: «Центральный угол сектора равен 45 градусов»; если это не так, измерьте центральный угол.
-
4
Используйте преобразованную формулу для вычисления площади круга. Если известны площадь сектора и его центральный угол, используйте следующую преобразованную формулу, чтобы найти площадь круга: [13]
-
5
-
6
Запишите ответ. В нашем примере сектор составлял одну восьмую полного круга. Поэтому площадь полного круга равна 120
см2. Так как площадь сектора дана с постоянной , скорее всего, ответ тоже можно представить с этой постоянной.[15]
- Чтобы записать ответ в численной форме, умножьте 120 x 3,14 = 376,8 см2.
Реклама
Об этой статье
Эту страницу просматривали 265 096 раз.
Была ли эта статья полезной?
В данном материале разберёмся, как найти площадь круга, и зачем это может пригодиться в реальной жизни.
Начнём с формулы, а затем рассмотрим из чего она состоит.
S=πR², где
- S – площадь
- π – число пи (математическая постоянная, равная отношению длины окружности к её диаметру). Значение π – 3,14 (сокращено до сотых).
- R – радиус круга. Сразу стоит упомянуть, что радиус равен половине диаметра.
Примеры
Рассмотрим несколько простых примеров расчёта площади круга.
Радиус круга равен 5 сантиметрам. Необходимо найти площадь круга.
- S = 3,14 х 5² = 78 см² (квадратных сантиметров).
Далее перейдём к практическим примерам. Дело в том, что недавно я убедился в том, что некоторые люди не очень хорошо понимают зависимость площади круга от его диаметра. Речь о выборе диаметра пиццы. Многие полагают, что между пиццей диаметром 30 и 40 см очень небольшая разница – четверть, а разница в цене более ощутимая. Но дело в том, что площадь пиццы отличается куда серьёзнее. Давайте посчитаем!
Сразу учтём, что радиус, используемый в формуле, это половина диаметра, рассчитывать отдельно не будем.
- S (30 см) = 3,14 * 15² = 706 см²
- S (40 см) = 3,14 * 20² = 1256 см²
Разница намного существеннее 25%, правда? Она составляет 1 — (1256 : 706) = 0,779 или 77,9%. Так что пицца 40 см примерно на три четверти больше пиццы 30 см, а не на одну. Давайте теперь сравним пиццу 20 см и пиццу 30 см.
- S (20 см) = 3,14 * 10² = 314 см²
- S (30 см) = 3,14 * 15² = 706 см²
Пицца 30 см в 2,248 раза (или на 124,8%) больше пиццы 20 см.
Разумеется, геометрии можно найти и куда более полезное применение. Но, надеюсь, теперь всё стало предельно понятно. А для расчёта просто запомните формулу — S=πR².
Содержание:
- Формула
- Примеры вычисления площади круга
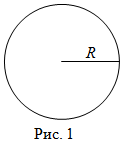
Формула
Чтобы найти площадь круга (рис. 1), надо найти произведение числа
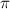на квадрат радиуса этого круга, то есть
$$mathrm{S}_{k p}=pi R^{2}$$
Напомним, что число $pi approx 3,1415926535 ldots$, а
радиусом круга называется отрезок, соединяющий центр круга с любой точкой ограничивающей его окружности.
Примеры вычисления площади круга
Пример
Задание. Найти площадь круга, если известно, что его радиус равен 3 м.
Решение. Площадь круга вычисляется по формуле:
$$mathrm{S}_{k p}=pi R^{2}$$
Подставляя в эту формулу значение радиуса $R=3$ м, получаем:
$mathrm{S}_{k p}=pi cdot 3^{2}=9 pi$ (м2)
Ответ. $mathrm{S}_{k p}=9 pi$ (м2)
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Чему равна площадь круга, если его диаметр равен 4 см?
Решение. Площадь круга найдем по формуле:
$$mathrm{S}_{k p}=pi R^{2}$$
Известно, что радиус круга связан с его диаметром соотношением:
$$d=2R$$
А тогда искомая площадь
$R=frac{d}{2}=frac{4}{2}=2$ (см2)
Ответ. $R=frac{d}{2}=2$ (см2)
Читать дальше: как найти площадь квадрата.
