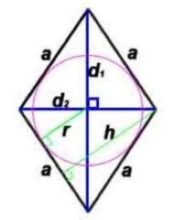
Как найти площадь окружности вписанной в ромб

Как найти площадь окружности вписанной в ромб

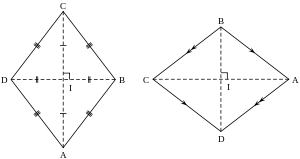
Ромб. Формулы, признаки и свойства ромба

Признаки ромба

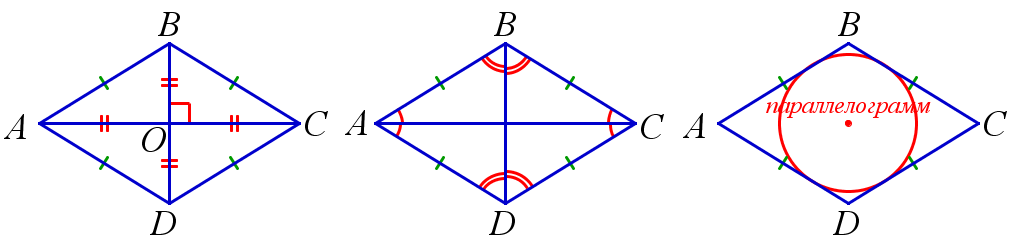
∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

2. Формула стороны ромба через площадь и синус угла:

3. Формула стороны ромба через площадь и радиус вписанной окружности:

4. Формула стороны ромба через две диагонали:

5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):

6. Формула стороны ромба через большую диагональ и половинный угол:

7. Формула стороны ромба через малую диагональ и половинный угол:

8. Формула стороны ромба через периметр:

Диагонали ромба

Формулы определения длины диагонали ромба:

d 1 = a √ 2 + 2 · cosα

d 1 = a √ 2 – 2 · cosβ

d 2 = a √ 2 + 2 · cosβ

d 2 = a √ 2 – 2 · cosα

d 1 = 2 a · cos ( α /2)

d 1 = 2 a · sin ( β /2)

d 2 = 2 a · sin ( α /2)

d 2 = 2 a · cos ( β /2)

7. Формулы диагоналей через площадь и другую диагональ:

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Площадь ромба

Формулы определения площади ромба:

4. Формула площади ромба через две диагонали:

5. Формула площади ромба через синус угла и радиус вписанной окружности:

6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):

S = 1 d 1 2 · tg ( α /2)
2
S = 1 d 2 2 · tg ( β /2)
2

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

6. Формула радиуса круга вписанного в ромб через две диагонали:

r = d 1 · d 2
2√ d 1 2 + d 2 2

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Вписанная в ромб окружность

Какими свойствами обладает вписанная в ромб окружность? Как найти её радиус?

Центр вписанной в ромб окружности — точка пересечения его диагоналей.

Радиус вписанной в ромб окружности можно найти по общей формуле

где S — площадь ромба, p — его полупериметр.

Так как полупериметр ромба равен p=2a, где a — сторона ромба, эту формулу можно записать как

С учётом формул для нахождения площади ромба:

где α — угол ромба (причем α может быть как острым, так и тупым).

где d1и d2 — диагонали ромба.

Таким образом, еще две формулы радиуса вписанной в ромб окружности:

Так как диаметр вписанной окружности равен высоте ромба, радиус равен половине высоты ромба:

Если известно, что точка касания вписанной окружности делит сторону ромба на отрезки, то радиус можно выразить через длины этих отрезков.

Так как диагонали ромба взаимно перпендикулярны и радиус, проведённый в точку касания, перпендикулярен стороне, то по свойству высоты прямоугольного треугольника из треугольника AOD имеем

Следовательно, радиус вписанной в ромб окружности есть среднее пропорциональное между отрезками, на которые делит сторону точка касания:

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d2b334caed19069 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

[spoiler title=”источники:”]

Вписанная в ромб окружность

http://mathvox.ru/geometria/mnogougolniki/glava-6-romb-i-ego-svoistva/ploschad-romba-i-vpisannaya-okrujnost-formula-1/

[/spoiler]

Источник

Improve Article

Save Article

Like Article

  • Read
  • Discuss

    • Improve Article

    Save Article

    Like Article

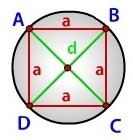
    Given a rhombus with diagonals a and b, which contains an inscribed circle. The task is to find the area of that circle in terms of a and b.
    Examples: 
     

    Input: l = 5, b = 6
    Output: 11.582

    Input: l = 8, b = 10
    Output: 30.6341

    Approach: From the figure, we see, the radius of inscribed circle is also a height h=OH of the right triangle AOB. To find it, we use equations for triangle’s area :
     

    Area AOB = 1/2 * (a/2) * (b/2) = ab/8 = 12ch

     where c = AB i.e. a hypotenuse. So, 

    r = h = ab/4c = ab/4√(a^2/4 + b^2/4) = ab/2√(a^2+b^2)

    and therefore area of the circle is
     

    A = Π * r^2 = Π a^2 b^2 /4(a2 + b2)

    Below is the implementation of above approach:
     

    C++

    #include <bits/stdc++.h>

    using namespace std;

    float circlearea(float a, float b)

    {

        if (a < 0 || b < 0)

            return -1;

        float A = (3.14 * pow(a, 2) * pow(b, 2))

                / (4 * (pow(a, 2) + pow(b, 2)));

        return A;

    }

    int main()

    {

        float a = 8, b = 10;

        cout << circlearea(a, b) << endl;

        return 0;

    }

    Java

    public class GFG {

        public static float circlearea(double a, double b)

        {

            if (a < 0 || b < 0)

                return -1 ;

            float A = (float) ((3.14 * Math.pow(a, 2) * Math.pow(b, 2))

                            / (4 * (Math.pow(a, 2) + Math.pow(b, 2)))) ;

            return A ;

        }

        public static void main(String[] args) {

            float a = 8, b = 10 ;

            System.out.println(circlearea(a, b));

        }

    }

    Python 3

    def circlearea(a, b):

        if (a < 0 or b < 0):

            return -1

        A = ((3.14 * pow(a, 2) * pow(b, 2))/

            (4 * (pow(a, 2) + pow(b, 2))))

        return A

    if __name__ == "__main__":

        a = 8

        b = 10

        print( circlearea(a, b))

    C#

    using System;

    public class GFG {

        public static float circlearea(double a, double b)

        {

            if (a < 0 || b < 0)

                return -1 ;

            float A = (float) ((3.14 * Math.Pow(a, 2) * Math.Pow(b, 2))

                            / (4 * (Math.Pow(a, 2) + Math.Pow(b, 2)))) ;

            return A ;

        }

        public static void Main() {

            float a = 8, b = 10 ;

            Console.WriteLine(circlearea(a, b));

        }

    }

    PHP

    <?php

    function circlearea($a, $b)

    {

        if ($a < 0 || $b < 0)

            return -1;

        $A = (3.14 * pow($a, 2) * pow($b, 2)) /

               (4 * (pow($a, 2) + pow($b, 2)));

        return $A;

    }

    $a = 8; $b = 10;

    echo circlearea($a, $b);

    ?>

    Javascript

    <script>

    function circlearea(a , b)

    {

        if (a < 0 || b < 0)

            return -1 ;

        var A =  ((3.14 * Math.pow(a, 2) * Math.pow(b, 2))

                        / (4 * (Math.pow(a, 2) + Math.pow(b, 2)))) ;

        return A ;

    }

    var a = 8, b = 10 ;

    document.write(circlearea(a, b).toFixed(4));

    </script>

    Time Complexity: O(1), as calculating squares using pow function is a constant time operation.
    Auxiliary Space: O(1), as no extra space is required

    Last Updated :
    25 Sep, 2022

    Like Article

    Save Article

    Источник

    Окружность, вписанная в ромб

    Ромб — это параллелограмм с четырьмя равными сторонами.

    Квадрат — частный случай ромба; это ромб, все углы которого прямые.

    Вписанная в ромб окружность — это окружность, которая лежит внутри ромба и касается всех его сторон.

    Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

    Окружность можно вписать в многоугольник, у которого равны суммы противолежащих сторон. Ромб соответствует этому условию, поэтому в ромб можно вписать окружность.

    окружность вписанная ромб

    Свойства ромба и вписанной окружности

    • в любой ромб можно вписать окружность;
    • точка пересечения диагоналей ромба является центром окружности, вписанной в ромб.

    Как найти радиус, основные способы

    Радиус вписанной окружности, если известны диагонали и сторона

    Радиус r вписанной в ромб окружности равен произведению его диагоналей, деленному на периметр или на сторону, умноженную на 4.

    Формула 1

    (r=frac{d_1d_2}Р=frac{d_1d_2}{4a})

    где r — радиус вписанной окружности,

    d1 и d2 — диагонали ромба,

    a — сторона ромба,

    Р — периметр ромба.

    Формула 1

    У изображенного ромба АВСD сторона равна а. Большая диагональ BD равна (d_1), меньшая диагональ АС равна (d_2). Радиус вписанной окружности:

    (r=frac{d_1d_2}{4a}=frac{BDcdot AC}{4cdot АВ}).

    Если известны только диагонали ромба

    Формула 2

    (r=frac{d_1d_2}{2sqrt{left(d_1right)^2+left(d_2right)^2}})

    где r — радиус вписанной окружности,

    d1 и d2 — диагонали ромба.

    Эту формулу можно получить из предыдущей.

    Диагонали ромба пересекаются под прямым углом, делятся точкой пересечения пополам, и разбивают ромб на четыре прямоугольных треугольника.

    Рассмотрим один из таких треугольников — ΔАВО. Сторона ромба АВ является гипотенузой ΔАВО.

    Если известны диагонали ромба BD, равная (d_1) и АС, равная (d_2), то катеты ВО и АО ΔАВО будут равны (frac{d_1}2) и (frac{d_2}2) соответственно.

    Выразим гипотенузу АВ треугольника АВО через его катеты ВО и АО.

    Согласно теореме Пифагора (АВ=sqrt{ВО^2+АО^2}=sqrt{left(frac{d_1}2right)^2+left(frac{d_2}2right)^2}).

    Подставив в формулу (r=frac{d_1d_2}p=frac{d_1d_2}{4a}) значение (а=sqrt{left(frac{d_1}2right)^2+left(frac{d_2}2right)^2}) и упростив выражение,

    получаем (r=frac{d_1d_2}{2sqrt{left(d_1right)^2+left(d_2right)^2}}).

    Если известны сторона и угол

    окружность вписанная ромб формула 3

    Радиус окружности, вписанной в ромб, равен половине произведения его стороны и синуса любого внутреннего угла ромба.

    Формула 3

    (r=frac{acdotsinalpha}2=frac{acdotsinbeta}2)

    где r — радиус вписанной окружности,

    α и β — внутренние углы ромба,

    a — сторона ромба.

    Если известна высота ромба

    окружность вписанная ромб формула 4

    Радиус вписанной в ромб окружности равен половине его высоты.

    Формула 4

    (r=frac h2)

    где r — радиус вписанной окружности,

    h — высота ромба.

    Из этой формулы следует, что высота ромба равна диаметру вписанной в него окружности.

    Если известны площадь ромба и его сторона

    Формула 5

    (r=frac S{2a}=frac Sр)

    где r — радиус вписанной окружности,

    S — площадь ромба,

    a — сторона ромба,

    р — полупериметр ромба.

    Вычисление радиуса через отрезки m и n

    отрезки м н

    Вписанная окружность касается стороны ромба. Точка касания делит сторону ромба на два отрезка. Пусть это будут отрезки m и n.

    Диагонали ромба взаимно перпендикулярны, ΔАОD — прямоугольный. Высота ΔАОD к стороне АD равна радиусу вписанной в ромб АВСD окружности.

    По свойству высоты прямоугольного треугольника, проведенной к гипотенузе, (ОК=sqrt{АКcdot КD}).

    Следовательно, радиус вписанной в ромб окружности равен среднему пропорциональному между отрезками, на которые делит сторону ромба точка касания.

    Формула 6

    (r=sqrt{mcdot n})

    где r — радиус вписанной окружности,

    m и n — отрезки, на которые делит сторону ромба точка касания.

    Задачи с решениями

    Задача 1

    Дано: ромб с диагоналями 6 см и 8 см.

    Найти: радиус вписанной в ромб окружности.

    Решение: так как известны диагонали ромба,

    применим формулу (r=frac{d_1d_2}{2sqrt{left(d_1right)^2+left(d_2right)^2}}). 

    (r=frac{6cdot8}{2sqrt{6^2+8^2}}=2,4 (см).)

    Ответ: радиус вписанной в ромб окружности равен 2,4 см.

    Задача 2

    Дано: ромб, сторона которого равна 16 см, а острый угол ромба — 30°.

    Найти: радиус вписанной в ромб окружности.

    Решение: применим формулу (r=frac{acdotsinalpha}2.)

    (r=frac{16cdot0,5}2=frac82=4 (см).)

     Ответ: радиус вписанной в ромб окружности равен 4 см.

    Источник

    Ромб — это параллелограмм, у которого все стороны равны. При этом трапеция обладает всеми свойствами четырехугольника и параллелограмма. Поэтому запоминать надо свойства, которые характерны для ромба.

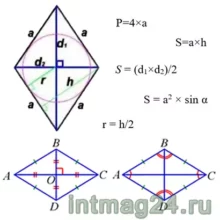
    Свойства ромба:

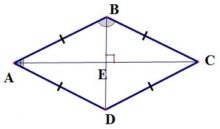
    1. Противоположные углы равны. На рисунке: ∠BAC=∠DAC=∠BCA=∠DCA, ∠ABD=∠CBD=∠ADB=∠CDB.
    2. Диагонали точкой пересечения делятся пополам. На рисунке: точка E.
    3. Диагонали ромба пересекаются под прямым углом. На рисунке: AC⊥BD
    4. Диагонали ромба являются биссектрисами его углов.

    Признаки ромба:

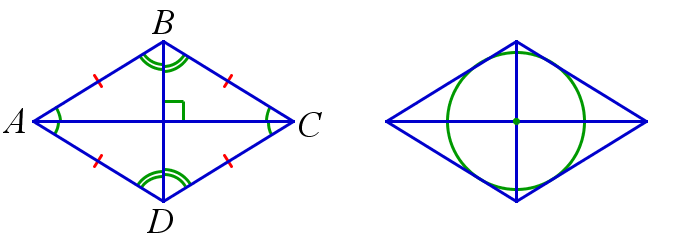
    1. Если диагонали четырёхугольника перпендикулярны и делятся точкой пересечения пополам, то этот четырёхугольник – ромб. На рисунке: AC⊥BD,AO=CO,BO=DO
    2. Если диагонали четырёхугольника лежат на биссектрисах его углов, то этот четырёхугольник – ромб. На рисунке: ∠BAC=∠DAC,∠BCA=∠DCA∠ABD=∠CBD,∠ADB=∠CDB.
    3. Если четырёхугольник — это параллелограмм и в него можно вписать окружность, то этот четырёхугольник – ромб. На рисунке: AB||CD,BC||AD,ABCD – описанный.

    Ромб и окружность

    В ромб можно вписать окружность. Центром этой окружности является точка пересечения диагоналей ромба.

    Радиус окружности, вписанной в ромб, можно найти по формуле: или где: a — длина стороны, d1, d2 –диагонали.

    Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°. Таким образом, ромб, вписанный в окружность – это квадрат. Центр окружности совпадает с точкой пересечения диагоналей.

    Основные формулы для ромба:

     Периметр: Площадь по стороне и высоте: Площадь по диагоналям: Радиус окружности, вписанной в ромб: или Площадь по стороне и радиусу вписанной окружности:

    Площадь по стороне и углу:

    где a — длина стороны, d1, d2 –диагонали, P-периметр, S-площадь,
    h -высота, проведенная к противоположной стороне
    α — угол между сторонами ромба.

    Источник

    У этого термина существуют и другие значения, см. Ромб (значения).

    Rhombus.svg

    Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1] (см. другие варианты определенияПерейти к разделу «Признаки»).

    Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

    Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

    Свойства[править | править код]

    • Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны: АВ || CD, AD || ВС. Противоположные углы ромба равны, а соседние углы дополняют друг друга до 180°.
    • Высоты в ромбе равны между собой.
    • Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре конгруэнтных прямоугольных треугольника.
    • Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
    • Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
    • Середины четырёх сторон ромба являются вершинами прямоугольника.
    • Диагонали ромба являются осями его симметрии.
    • В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

    Признаки[править | править код]

    Самое общее определение: ромб — это выпуклый четырёхугольник[2], все стороны которого равны друг другу. Можно показать, что такой четырёхугольник является параллелограммом[3][1].

    Параллелограмм ABCD является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[4]:

    • Две его смежные стороны равны (отсюда следует, что все стороны равны).
    • Его диагонали пересекаются под прямым углом.
    • Одна из диагоналей делит содержащие её углы пополам. Другими словами, диагональ является биссектрисой противоположных углов.
    • Диагонали параллелограмма делят его на четыре равных между собой треугольника.
    • Диагонали параллелограмма являются осями симметрии[5].

    Помимо всего, ромб можно рассматривать как частный случай дельтоида, у которого любые две смежные стороны равны между собой.

    Квадрат как частный случай ромба[править | править код]

    Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.

    Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[6][7].

    Уравнение ромба[править | править код]

    К уравнению ромба (центр в начале координат)

    Уравнение ромба с центром в точке {displaystyle {x_{0},y_{0}}} и диагоналями, параллельными осям координат, может быть записано в виде[8]:

    {displaystyle {frac {|x-x_{0}|}{a}}+{frac {|y-y_{0}|}{b}}=1,}

    где a,b — половины длин диагоналей ромба по осям X,Y соответственно.

    Длина стороны ромба равна {displaystyle {sqrt {a^{2}+b^{2}}}.} Площадь ромба равна {displaystyle 2ab.} Левый угол ромба рассчитывается по формуле:

    {displaystyle 2operatorname {arctg} {frac {b}{a}}}

    Второй угол дополняет его до 180°.

    В случае a = b уравнение отображает повёрнутый на 45° квадрат:

    {displaystyle |x-x_{0}|+|y-y_{0}|=a,}

    где сторона квадрата равна {displaystyle a{sqrt {2}},} а его диагональ равна {displaystyle 2a.} Соответственно площадь квадрата равна {displaystyle 2a^{2}.}

    Из уравнения видно, что ромб можно рассматривать[8] как суперэллипс степени 1.

    Площадь ромба[править | править код]

    Rhombus1.svg

    • Площадь ромба равна половине произведения его диагоналей.
    {displaystyle S={dfrac {ACcdot BD}{2}}}
    • Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
    {displaystyle S=acdot h}
    • Кроме того, площадь ромба может быть вычислена по формуле:
    {displaystyle S=a^{2}cdot sin alpha },

    где alpha  — угол между двумя смежными сторонами ромба.

    • Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол alpha :
    {displaystyle S={dfrac {4r^{2}}{sin alpha }};}
    • Площадь ромба равна удвоенному произведению стороны и радиуса вписанной окружности:
    {displaystyle S=2ar.}

    Радиус вписанной окружности[править | править код]

    Радиус вписанной окружности r может быть выражен через диагонали p и q в виде[9]:

    {displaystyle r={frac {pcdot q}{2{sqrt {p^{2}+q^{2}}}}}.}

    В геральдике[править | править код]

    Ромб является простой геральдической фигурой.

    • Червлёный ромб в серебряном поле

      Червлёный ромб в серебряном поле

    • В червлёном поле 3 сквозных ромба: 2 и 1

      В червлёном поле 3 сквозных ромба: 2 и 1

    • Просверленный червлёный ромб в серебряном поле

      Просверленный червлёный ромб в серебряном поле

    • В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

      В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

    Симметрия[править | править код]

    Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.

    • Ромбический орнамент

      Ромбический орнамент

    • Ромбические звёзды

      Ромбические звёзды

    • Более сложный орнамент

      Более сложный орнамент

    • Мозаика Пенроуза

    См. другие примеры на Викискладе.

    См. также[править | править код]

    • Дельтоид
    • Звезда (геометрия)
    • Ромбододекаэдр
    • Ромбоид

    Примечания[править | править код]

    1. ↑ 1 2 Элементарная математика, 1976, с. 435..
    2. ↑ Требование выпуклости нужно, чтобы исключить случаи вырожденного четырёхугольника, у которого часть вершин совпадают (например, фигура, имеющая вид буквы V и ромбом не являющаяся).
    3. ↑ Погорелоа А. В. Домашняя работа по геометрии за 8 класс. М.: Просвещение, 2001, С. 18.
    4. ↑ Элементарная математика, 1976, с. 435—436..
    5. ↑ Шахмейстер А. Х. Треугольники и параллелограммы // Геометрические задачи на экзаменах. Часть 1. Планиметрия : книга / А. Х. Шахмейстер. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2015. — С. 26. — 392 с. : илл. — (Математика. Элективные курсы). — 1500 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-98712-083-5. — ISBN 978-5-91673-155-2. — ISBN 978-5-4439-0347-7.
    6. ↑ Ромб // Малый академический словарь. — М.: Институт русского языка Академии наук СССР. Евгеньева А. П.. 1957—1984.
    7. ↑ Чудинов А. Н. Ромб // Словарь иностранных слов, вошедших в состав русского языка. 1910.
    8. ↑ 1 2 Weisstein, Eric W. Superellipse (англ.) на сайте Wolfram MathWorld. Здесь ромб назван diamond.
    9. ↑ Weisstein, Eric W. Rhombus (англ.) на сайте Wolfram MathWorld.

    Литература[править | править код]

    • Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
    • Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
    Источник

    Добавить комментарий