Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given a regular Hexagon with side length a, the task is to find the area of the circle inscribed in it, given that, the circle is tangent to each of the six sides.
Examples:
Input: a = 4 Output: 37.68 Input: a = 10 Output: 235.5

Approach:
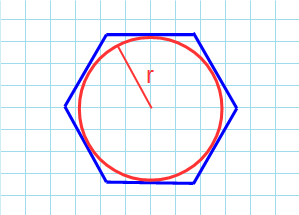
From the figure, it is clear that, we can divide the regular hexagon into 6 identical equilateral triangles.
We take one triangle OAB, with O as the centre of the hexagon or circle, & AB as one side of the hexagon.
Let M be mid-point of AB, OM would be the perpendicular bisector of AB, angle AOM = 30 deg
Then in right angled triangle OAM,
tanx = tan30 = 1/√3
So, a/2r = 1/√3
Therefore, r = a√3/2
Area of circle, A =Πr²=Π3a^2/4
Below is the implementation of the approach:
C++
#include <bits/stdc++.h>
using namespace std;
float circlearea(float a)
{
if (a < 0)
return -1;
float A = (3.14 * 3 * pow(a, 2)) / 4;
return A;
}
int main()
{
float a = 4;
cout << circlearea(a) << endl;
return 0;
}
Java
import java.util.*;
class solution
{
static double circlearea(double a)
{
if (a < 0)
return -1;
double A = (3.14 * 3 * Math.pow(a,2) ) / 4;
return A;
}
public static void main(String arr[])
{
double a = 4;
System.out.println(circlearea(a));
}
}
Python 3
def circlearea(a) :
if a < 0 :
return -1
A = (3.14 * 3 * pow(a,2)) / 4
return A
if __name__ == "__main__" :
a = 4
print(circlearea(a))
C#
using System;
class GFG
{
static double circlearea(double a)
{
if (a < 0)
return -1;
double A = (3.14 * 3 *
Math.Pow(a, 2)) / 4;
return A;
}
public static void Main()
{
double a = 4;
Console.WriteLine(circlearea(a));
}
}
PHP
<?php
function circlearea($a)
{
if ($a < 0)
return -1;
$A = (3.14 * 3 * pow($a, 2)) / 4;
return $A;
}
$a = 4;
echo circlearea($a) . "n";
Javascript
<script>
function circlearea(a) {
if (a < 0)
return -1;
var A = (3.14 * 3 * Math.pow(a, 2)) / 4;
return A;
}
var a = 4;
document.write(circlearea(a));
</script>
Time complexity: O(1)
Auxiliary Space: O(1)
Last Updated :
20 Aug, 2022
Like Article
Save Article
Ответ:
75π см².
Объяснение:
ABCDEF – правильный шестиугольник со стороной 10 см.
Рассмотрим Δ AOB – равносторонний , AO=BO=AB= 10 см.
OH – радиус вписанной окружности и высота Δ AOB. Высота равностороннего треугольника определяется по формуле:
, где a- сторона треугольника. Тогда
см.
Значит радиус окружности, вписанной в данный шестиугольник
см.
Площадь круга найдем по формуле :
см²
Как найти площадь вписанной окружности
Площадь окружности, вписанной в многоугольник, можно вычислить не только через параметры самой окружности, но через различные элементы описанной фигуры – стороны, высоту, диагонали, периметр.

Инструкция
Окружность называется вписанной в многоугольник, если имеет общую точку с каждой стороной описанной фигуры. Центр вписанной в многоугольник окружности всегда лежит в точке пересечения биссектрис его внутренних углов. Площадь, ограниченная окружностью, определяется формулой S=π*r²,
где r – радиус окружности,
π – число «Пи» – математическая постоянная, равная 3,14.
Для окружности, вписанной в геометрическую фигуру, радиус равен отрезку от центра до точки касания со стороной фигуры. Следовательно, можно определить зависимость между радиусом вписанной в многоугольник окружности и элементами данной фигуры и выразить площадь окружности через параметры описанного многоугольника.
В любой треугольник возможно вписать единственную окружность с радиусом, определяемым формулой: r=s∆/p∆,
где r – радиус вписанной окружности,
s∆ – площадь треугольника,
p∆ – полупериметр треугольника.
Подставьте полученное значение радиуса, выраженное через элементы описанного около окружности треугольника, в формулу площади окружности. Тогда площадь S окружности, вписанной в треугольник с площадью s∆ и полупериметром p∆ вычисляется по формуле:
S = π*(s∆/p∆)².
Окружность можно вписать в выпуклый четырехугольник при условии, что в нем равны суммы противолежащих сторон.
Площадь S окружности, вписанной в квадрат со стороной a, равна: S= π*a²/4.
В ромбе площадь S вписанной окружности равна: S= π*(d₁d₂/4a)². В этой формуле d₁ и d₂ — диагонали ромба, а – сторона ромба.
Для трапеции площадь S вписанной в нее окружности определяется по формуле: S= π*(h/2)², где h – высота трапеции.
Сторона а правильного шестиугольника равна радиусу вписанной в него окружности, площадь S окружности вычисляется по формуле: S = π*a².
Окружность можно вписать в правильный многоугольник с любым количеством сторон. Общая формула для определения радиуса r окружности, вписанной в многоугольник со стороной а и числом сторон n: r=a/2tg(360°/2n). Площадь S вписанной в такой многоугольник окружности: S=π*(a/2tg(360°/2n)²/2.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
На этой странице вы найдете калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного шестиугольника по стороне или радиусам вписанной и описанной окружностей.
Шестиугольник представляет собой многоугольник, к которого все внутренние углы равны 120 градусов, а все стороны равны между собой.
Содержание:
- калькулятор площади правильного шестиугольника
- формула площади правильного шестиугольника через длину стороны
- формула площади правильного шестиугольника через радиус вписанной окружности
- формула площади правильного шестиугольника через радиус описанной окружности
- формула площади правильного шестиугольника через периметр
- примеры задач
Формула площади правильного шестиугольника через длину стороны
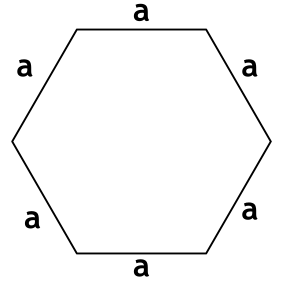
S = dfrac{3 sqrt{3} a^2}{2}
a – длина стороны шестиугольника
Формула площади правильного шестиугольника через радиус вписанной окружности
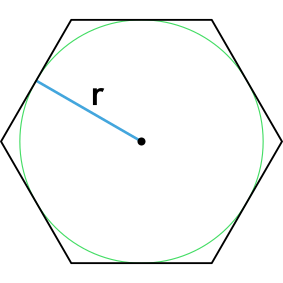
S = 2 sqrt{3}r^2
r – радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности

S = dfrac{3 sqrt{3} R^2}{2}
R – радиус описанной окружности
Формула площади правильного шестиугольника через периметр

S = dfrac{P^2 sqrt{3}}{24}
P – периметр шестиугольника
Примеры задач на нахождение площади правильного шестиугольника
Задача 1
Найдите площадь правильного шестиугольника, радиус вписанной окружности которого равен 9 см.
Решение
Исходя из того, что из условия задачи нам известен радиус вписанной окружности, мы воспользуемся формулой.
S = 2 sqrt{3}r^2 = 2 sqrt{3} cdot 9^2 = 2 sqrt{3} cdot 81 = 162 sqrt{3} : см^2 approx 280.59223 : см^2
Ответ: 162 sqrt{3} : см^2 approx 280.59223 : см^2
Проверить правильность решения нам поможет калькулятор .
Задача 2
Найдите площадь правильного шестиугольника со стороной равной 1 см.
Решение
Для этой задачи нам подойдет формула.
S = dfrac{3 sqrt{3} a^2}{2} = dfrac{3 sqrt{3} cdot 1^2}{2} = dfrac{3 sqrt{3} cdot 1}{2} = dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Ответ: dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Проверим ответ .
Как рассчитать площадь правильного шестиугольника
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник – многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
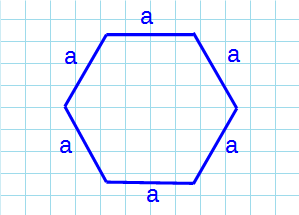
a:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через сторону:
a – сторона шестиугольника.
Через радиус описанной окружности
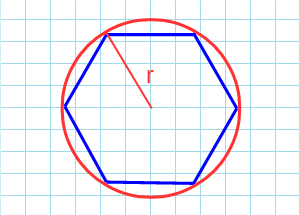
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
r – радиус описанной окружности.
Через радиус вписанной окружности
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
r – радиус вписанной окружности.
