Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности: 
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: 
отсюда 
.
После того, как найдем диагональ – мы сможем рассчитать радиус: 
.
И после подставим все в основную формулу площади круга описанного вокруг квадрата: 
Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
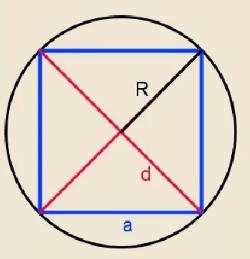
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.
Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Ответ:
128·π см²
Объяснение:
Дано (см. рисунок):
a=16 см – сторона квадрата
Найти: S – площадь круга.
Решение.
Радиус окружности (круга), описанной около квадрата связана со стороной a следующей формулой:
Тогда радиус круга, описанного около квадрата со стороной 16 см равен см.
Площадь круга определяется через радиус по формуле:
Теперь находим нужную площадь круга: см².
|
Как известно, чтобы вычислить площадь круга надо знать только одну величину – его радиус или диаметр. Поэтому однотипные задачи по нахождению площади окружности описанной вокруг квадрата, прямоугольника или треугольника сводятся к нахождению именно этой величины. Если с квадратом и прямоугольником все достаточно просто – центром описанной окружности будет точка пересечения диагоналей этих четырехугольников, то с треугольником сложнее – центр описанной окружности расположится в точке пересечения его медиан. Поэтому радиус круга описанного вокруг прямоугольника находится через теорему Пифагора. Для квадрата это: R=0.5*a*√‾2 Для прямоугольника: R=0.5*√‾(а*а+b*b) Ну а для любого треугольника ищем радиус круга через теорему синусов: R=a/(2*sin(A)) Ну а далее находим площадь круга по стандартной формуле: S=π*r2 система выбрала этот ответ лучшим
дольфаника 8 лет назад Если надо найти площадь описанного круга вокруг, например, квадрата, то надо воспользоваться выведенной уже очень давно формулой Площадь = число пи умножить на радиус в квадрате Можно еще по другой формуле высчитать площадь описанного вокруг треугольника круга. Формула подходит для расчета площади круга через диаметр
Знаете ответ? |
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Содержание
- Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
- Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
- Площадь круга, описанного около квадрата: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
- Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
- Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
- Видео: Математика | Вычисление площадей круга и его частей
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:
Примеры решения заданий по нахождению S-площади круга через R-радиус:
————————————————————————————————————————
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:
Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Площадь круга, вписанного в квадрат: формула, примеры решения задач
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Решайте так: Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Площадь круга, описанного около квадрата: формула, примеры решения задач
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
Формулы площади круга вписанного и описанного в треугольник и квадрат.
Площадь круга. Площадь круга вписанного в треугольник и квадрат (описанного около).
Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов
Обозначения:
A, B, C — углы,
a, b, c — стороны,
h — высота,
R — радиус,
S — площадь.
p — полупериметр.
Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов
1. Площадь круга
Где S — площадь круга, R — радиус круга.
2. Площадь круга вписанного в квадрат.
Где a/2 — радиус круга, a — длина стороны квадрата.
3. Площадь круга описанного около квадрата.
Где a — длина стороны квадрата.
В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3.
4. Площадь круга вписанного в треугольник.
Используя формулу радиуса вписанной окружности
R = (p-a)*tg(A/2)
Где a, A — сторона и противолежащий угол соответственно, p — полупериметр.
Можем записать формулу площади круга вписанного в треугольник:
S = пи * ((p-a)*tg(A/2))²
5. Площадь круга описанного около треугольника.
Используя формулу радиуса описанной окружности
R = a/(2*sin(A))
Где a, A — сторона и противолежащий угол соответственно.
Можем записать формулу площади круга описанного около треугольника:
S = пи * (a/(2*sin(A)))²
6. Формулы полезные в жизни
Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича.
Площадь круга
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: 
отсюда 
.
После того, как найдем диагональ – мы сможем рассчитать радиус: 
.
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Площадь круга: как найти, формулы
О чем эта статья:
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Ответ: 113,04 см 2 .
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Ответ: 6358,5 мм 2 .
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Ответ: 18,84 см 2 .
[spoiler title=”источники:”]
http://2mb.ru/matematika/geometriya/ploshhad-kruga/
http://skysmart.ru/articles/mathematic/ploshad-kruga
[/spoiler]
