Как найти площадь описанной окр около квадрата

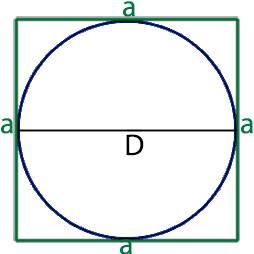
Онлайн калькулятор площади квадрата описанного около окружности. Как узнать площадь квадрата описанного около окружности.

Вычислить площадь квадрата описанного около окружности через:

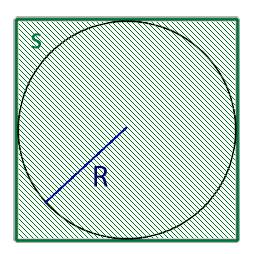
Радиус круга R:

Для того, что бы узнать площадь квадрата описанного около окружности необходимо с тем что у этих двух фигур общее, а одной из общих величин у них является сторона квадрата которая равна диаметру круга.

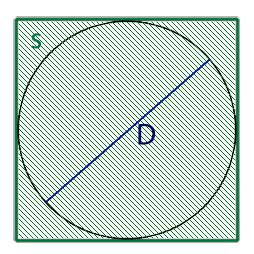
Таким образом для нахождения площади квадрата описанного около окружности, через этот круг, необходимо найти значение диаметра.

Для нахождения диаметра окружности нам необходимо знать одну из его величин а именно:

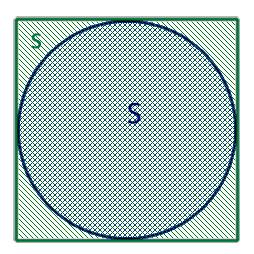
1. либо площадь круга, обозначаемая буквой S,
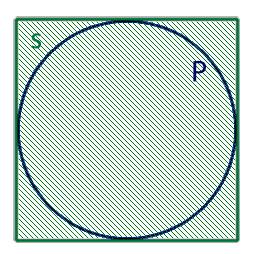
2. либо периметр круга, обозначаемый буквой P,
3. либо радиус круга, обозначаемый буквой R,

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

Соответственно если мы знаем диаметр круга который равен стороне описанного квадрата,

Теперь мы можем узнать площадь этого квадрата

Как определить площадь квадрата

О чем эта статья:

3 класс, 8 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Формула нахождения площади квадрата

Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

S = a × a = a 2 , где S — площадь, a — сторона.

Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d 2 : 2, где d — диагональ.

Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

S = 4 × r 2 , где r — это радиус вписанной окружности.

Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

S = 2 × R 2 , где R — это радиус описанной окружности.

У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р 2 : 16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Популярные единицы измерения площади:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Воспользуемся формулой: S = d 2 : 2.

Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .

Ответ: 4050 мм 2 .

Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.

Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d

Диаметр окружности равен двум радиусам:
d = 2r

Получается, что сторона равна двум радиусам:
a = 2r

Используем формулу нахождения площади квадрата через сторону:
S = a 2

Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2

Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Окружность, описанная около квадрата

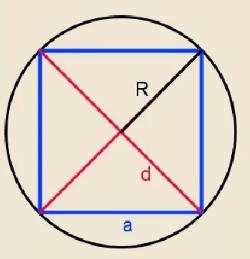
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/ploshad-kvadrata

http://matworld.ru/geometry/kvadrat.php

[/spoiler]

Здравствуйте, уважаемые читатели. Продолжаем разбор заданий с окружностью. В этой статье рассмотрим задачи на вписанную окружность в квадрат и описанную около квадрата.

1. Центральные и вписанные углы.

2.Касательная, хорда, секущая.

3.Вписанная и описанная окружность (треугольник)

4. Вписанная и описанная окружность (квадрат)

Все задачи такого типа достаточно простые. Приступим сразу же к решению задач.

Задача №1

Решение:

Радиус окружности – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.

Решение к этой задачи представлю в виде картинки.

О – центр окружности, r – радиус окружности. В этой задаче радиус окружности равен половине стороны квадрата. Ответ 8.

Задача №2

Найдите площадь квадрата, описанного вокруг окружности радиуса 9

Решение:

Задача обратная той, что мы решили выше. Так как радиус окружности равен 9, то сторона квадрата равна 18. Площадь квадрата равна:

Задача №3

Решение:

В предыдущих задачах мы определили, что если известен радиус вписанной окружности в квадрат, то сторона квадрата будет равна удвоенному значению радиуса.

Зная сторону квадрата, диагональ квадрата найдем, используя теорему Пифагора.

Задача №4

Решение:

Эта задача, включает в себя все этапы, которые были разобраны выше. Задачу можно разбить на действия:

1) Найдем сторону квадрата.

2) Найдем диагональ квадрата.

3) Найдем радиус описанной окружности, разделив диагональ квадрата пополам.

1) Найдем сторону квадрата:

2) Найдем диагональ квадрата используя теорему Пифагора:

3) Найдем радиус описанной окружности, разделив диагональ квадрата пополам.

Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Для того, что бы узнать площадь квадрата описанного около окружности необходимо с тем что у этих двух фигур общее, а одной из общих величин у них является сторона квадрата которая равна диаметру круга.

a=D

Таким образом для нахождения площади квадрата описанного около окружности, через этот круг, необходимо найти значение диаметра.

Для нахождения диаметра окружности нам необходимо знать одну из его величин а именно:

1. либо площадь круга, обозначаемая буквой S,
2. либо периметр круга, обозначаемый буквой P,
3. либо радиус круга, обозначаемый буквой R,

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=P/π

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=2R

Соответственно если мы знаем диаметр круга который равен стороне описанного квадрата,

a=D

Теперь мы можем узнать площадь этого квадрата

p = a²

Задания

Версия для печати и копирования в MS Word