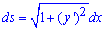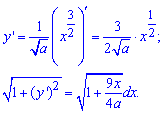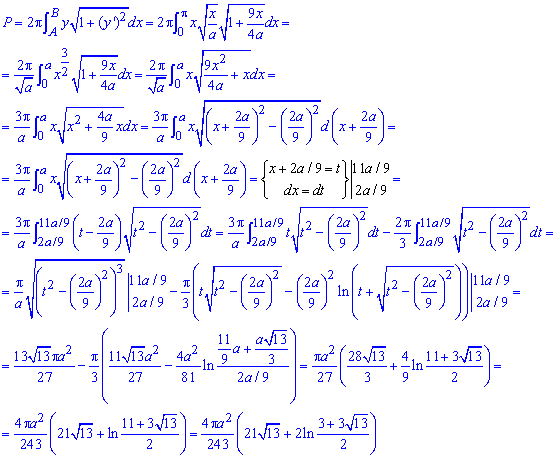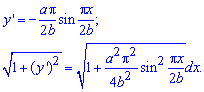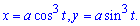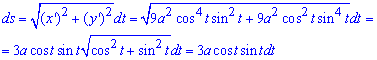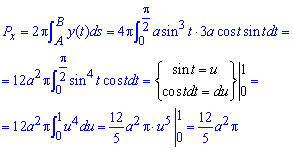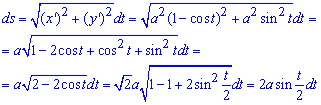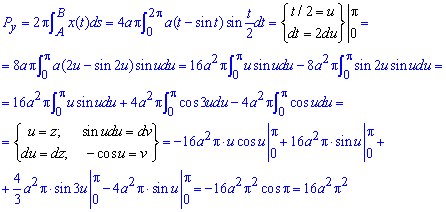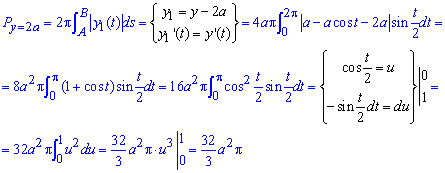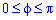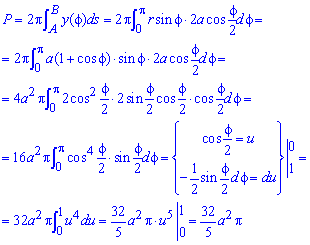Сечение цилиндра: определение, виды, его образующая
Содержание:
- Кратко о цилиндре
- Осевое сечение
- Как найти площадь сечения
- Осевое сечение наклонного цилиндра
-
Примеры задач
- Задача 1
- Задача 2
Кратко о цилиндре
Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.
Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.
Осевое сечение
Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти площадь сечения
Формула 1
(S = d*h,)
где (d) — диаметр, а (h) — высота всей фигуры.
Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).
Формула 2
(S = a*h, )
где (a) — хорда.
Осевое сечение наклонного цилиндра
Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.
Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:
(S = d * b * sin(α))
Примеры задач
Рассмотрим пару задач на осевое сечение с решениями.
Задача 1
Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?
Решение
Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:
(Sц = 2pi * r * (r + h))
Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:
(Sц = 2pi * r * (r + 2r) = 6 * pi * r²)
Исходя из этого, будем выражать радиус:
(r = √(Sц / (6*pi)))
Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:
(S = (2*r)2 = 4*r2 = 2*Sц/ (3*pi))
Подставим известные данные ((Sц = 100см^2)) и получим площадь сечения (S = 21,23 см²).
Ответ: (S = 21,23 см²).
Задача 2
Дано: ABCD — осевое сечение цилиндра. Площадь сечения (Sc) равна (10 м²), а площадь основания (Sо— 5 м²). Найти высоту цилиндра.
Решение
Так как площадь основания — круг, то (Sо = pi * r²). Тогда (r = √(Sо/pi) = √(5/pi).)
Так как площадь сечения — прямоугольник, то (Sc = AB * BC = h * 2r.) Тогда (h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).)
Ответ: (h = √(5pi).)
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
На этой странице вы сможете рассчитать площадь эллипса. Для этого необходимо знать длины полуосей или осей – просто введите их в поля калькулятора и получите результат. Кроме этого вы можете найти площадь эллипса самостоятельно по формулам, которые мы также публикуем на этой странице.
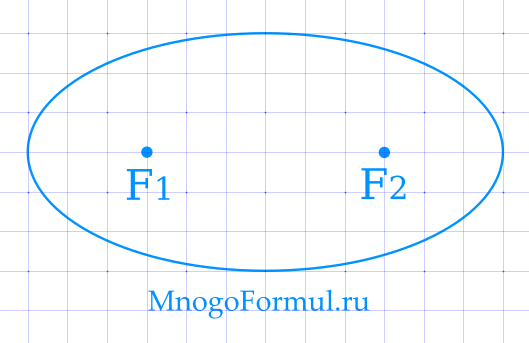
Эллипс — замкнутая кривая на плоскости, которую можно получить пересечением цилиндра плоскостью.
Эллипс можно определить как замкнутую плоскую кривую, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
Формула площади эллипса через полуоси
S = pi Rr
R – большая полуось эллипса
r – малая полуось эллипса
Формула площади эллипса через оси
S= pi dfrac{dD}{4}
D – большая ось эллипса
d – малая ось эллипса
Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x=a, x=b, а также непрерывной (неотрицательной или неположительной) функцией y=f(x). Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t. В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.
После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.
Основная формула для вычисления
Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x=a, x=b, ось Ox и параметрически заданная кривая x=φ(t)y=ψ(t), а функции x=φ(t) и y=ψ(t) являются непрерывными на интервале α; β, α<β, x=φ(t) будет непрерывно возрастать на нем и φ(α)=a, φ(β)=b.
Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S(G)=∫αβψ(t)·φ'(t)dt.
Мы вывели ее из формулы площади криволинейной трапеции S(G)=∫abf(x)dx методом подстановки x=φ(t)y=ψ(t):
S(G)=∫abf(x)dx=∫αβψ(t)d(φ(t))=∫αβψ(t)·φ'(t)dt
Учитывая монотонное убывание функции x=φ(t) на интервале β; α, β<α, нужная формула принимает вид S(G)=-∫βαψ(t)·φ'(t)dt.
Если функция x=φ(t) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.
Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой
В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.
Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x=2cos ty=3sin t.
Решение
У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3. См на иллюстрацию:
Попробуем найти площадь 14 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x∈a; b=0; 2. Далее умножим полученное значение на 4 и найдем площадь целой фигуры.
Вот ход наших вычислений:
x=φ(t)=2cos ty=ψ(t)=3sin tφα=a⇔2cos α=0⇔α=π2+πk, k∈Z,φβ=b⇔2cos β=2⇔β=2πk, k∈Z
При k, равном 0, мы получим интервал β; α=0; π2. Функция x=φ(t)=2cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:
-∫0π23 sin t·2cos t’dt=6∫0π2sin2t dt=3∫0π2(1-cos(2t)dt==3·t-sin(2t)20π2=3·π2-sin2·π22-0-sin2·02=3π2
Значит, площадь фигуры, заданной исходной кривой, будет равна S(G)=4·3π2=6π.
Ответ: S(G)=6π
Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x∈a; b=-2; 2. В этом случае у нас бы получилось:
φ(α)=a⇔2cos α=-2⇔α=π+πk, k∈Z,φ(β)=b⇔2cos β=2⇔β=2πk, k∈Z
Таким образом, при k равном 0, мы получили β; α=0; π. Функция x=φ(t)=2cos t на этом интервале будет монотонно убывать.
После этого вычисляем площадь половины эллипса:
-∫0π3sin t·2cos t’dt=6∫0πsin2t dt=3∫0π(1-cos(2t)dt==3·t-sin(2t)20π=3·π-sin2·π2-0-sin2·02=3π
Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.
Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x=a·cos ty=b·sin t. Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса Sэлипса=πab.
Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x=R·cos ty=R·sin t, где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R: Sкруга=πR2.
Разберем еще одну задачу.
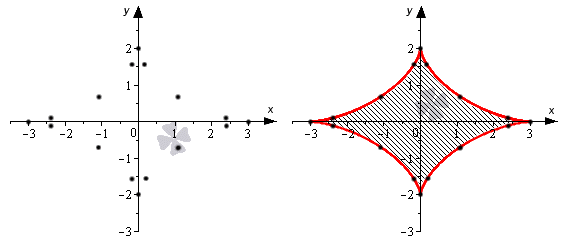
Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x=3cos3ty=2sin3t.
Решение
Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x=a·cos3ty=a·sin3t.
Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.
У нас x=φ(t)=3cos3t, y=ψ(t)=2sin3t.
Данные функции являются определенными для всех действительных значений t. Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x=φ(t)=3cos3t, y=ψ(t)=2sin3t для некоторых t=t0∈0; 2π π8, π4, 3π8, π2,…, 15π8, получим точки x0; y0=(φ(t0); ψ(t0)).
Составим таблицу итоговых значений:
| t0 | 0 | π8 | π4 | 3π8 | π2 | 5π8 | 3π4 | 7π8 | π |
| x0=φ(t0) | 3 | 2.36 | 1.06 | 0.16 | 0 | -0.16 | -1.06 | -2.36 | -3 |
| y0=ψ(t0) | 0 | 0.11 | 0.70 | 1.57 | 2 | 1.57 | 0.70 | 0.11 | 0 |
| t0 | 9π8 | 5π4 | 11π8 | 3π2 | 13π8 | 7π4 | 15π8 | 2π |
| x0=φ(t0) | -2.36 | -1.06 | -0.16 | 0 | 0.16 | 1.06 | 2.36 | 3 |
| y0=ψ(t0) | -0.11 | -0.70 | -1.57 | -2 | -1.57 | -0.70 | -0.11 | 0 |
После этого отметим нужные точки на плоскости и соединим их одной линией.
Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x∈a; b=0; 3:
φ(α)=a⇔3cos3t=0 ⇔α=π2+πk, k∈Z,φ(β)=b⇔3cos3t=3⇔β=2πk, k∈Z
Если k равен 0, то у нас получится интервал β; α=0; π2, и функция x=φ(t)=3cos3t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:
-∫0π22sin3t·3cos3t’dt=18∫0π2sin4t·cos2tdt==18∫0π2sin4t·(1-sin2t)dt=18∫0π2sin4tdt-∫0π2sin6tdt
У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу Jn(x)=-cos x·sinn-1(x)n+n-1nJn-2(x), где Jn(x)=∫sinnxdx.
∫sin4tdt=-cos t·sin3t4+34∫sin2tdt==-cos t·sin3t4+34-cos t·sin t2+12∫sin0tdt==-cos t·sin3t4-3cos t·sin t8+38t+C⇒∫0π2sin4tdt=-cos t·sin3t4-3cos t·sin t8+38t0π2=3π16∫sin6tdt=-cos t·sin5t6+56∫sin4tdt⇒∫0π2sin6tdt=-cos t·sin5t60π2+56∫0π2sin4tdt=56·3π16=15π96
Мы вычислили площадь четверти фигуры. Она равна 18∫0π2sin4tdt-∫0π2sin6tdt=183π16-15π96=9π16.
Если мы умножим это значение на 4, получим площадь всей фигуры – 9π4.
Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x=a·cos3ty=a·sin3t, можно найти по формуле Sастроиды=3πa28, а площадь фигуры, которая ограничена линией x=a·cos3ty=b·sin3t, считается по формуле S=3πab8.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Площадь поверхности P, что образована вращением гладкой кривой AB вокруг оси Ox где y(x) – непрерывная гладкая функция равняется
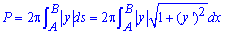
Основные формулы теории расчета площади поверхности Вы имеете, теперь перейдем к примерам, что Вас ожидают на практике и экзаменах.
Задание подобрано из учебной программы для студентов мех-мату Львовского национального университета имени Ивана Франко.
Другие Вузы имеют подобную программу учебы, задания похожие, а в ряде случаев те же.
Номера в примерах отвечает номеру из сборника Б. П. Демидовича. Для изучения основных моментов формулы интегрирования для вычисления площади поверхности вращения будут повторяться из примера в пример.
Часть заданий проиллюстрируем графиками кривых.
Пример 2486 Найти площадь поверхности вращения кривой 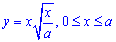
Решение: Найдем дифференциал дуги:
для этого вычисляем производную функции и, возведя к квадрату, подставляем в формулу
Запишем пределы интегрирования (известно за условием):
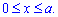
Интегрированием находим площадь поверхности вращения:
Как видите больше всего трудностей возникает при нахождении интеграла.
Здесь пришлось выделить полные квадраты под корнем, а дальше перейти к новой переменной под интегралом.
Не забывайте, что это приводит к изменению пределов интегрирования. Также здесь и в следующих примерах будем искать лишь интеграл, то что площадь измеряется в единицах квадратных Вы должны знать еще из школы.
Пример 2487 Найти площадь поверхности вращения кривой 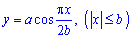
Решение: Вычисляем дифференциал дуги кривой:
За условием предела интегрирования: xє[-b;b].
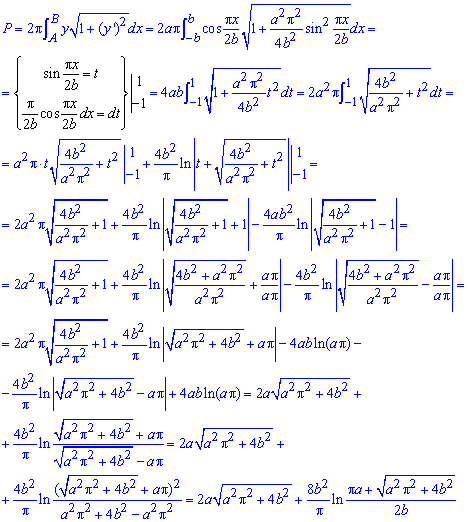
За формулой находим площадь поверхности вращения:
Здесь также под интегралом переходим к новой переменной, дальше после возведения к табличным интегралам подставляем пределы и упрощаем логарифмы.
Пример 2492 Найти площадь поверхности вращения астроиды 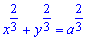
Решение: Записываем уравнение астроиды в параметрическом виде:
Находим дифференциал дуги параметрически заданной кривой по формуле:
Заметьте, что для параметрически заданной кривой формула несколько иная.
Запишем пределы интегрирования: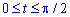
Вычислим площадь поверхности вращения:
Замена переменных упрощает интегрирование.
Пример 2495 Найти площадь поверхности вращения кривой, заданной параметрически x=a(t-sin (t)), y=a(1-cos(t)), t[0;2pi]
а) вокруг оси Ox;
б) вокруг оси Oy;
в) вокруг прямой y=2a.
Решение: Найдем дифференциал дуги параметрически заданной кривой:
При упрощении использовали известные тригонометрические зависимости.
Пределы интегрирования:
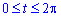
Найдем площадь поверхности вращения вокруг осей:
а) 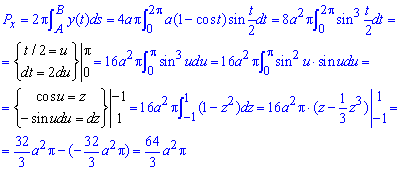
б)
в) площадь поверхности вращения вокруг прямой y=2a
Здесь использовали симметрию относительно прямой x1=a*Pi, поэтому результат умножили на 2.
Пример 2497 Найти площадь поверхности вращения кардиоиды 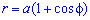

Решение: Для кривой заданной в полярных координатах дифференциал дуги находим по формуле:
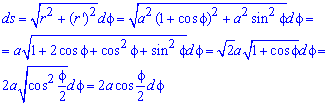
Пределы интегрирования:
Вычислим площадь поверхности вращения кардиоиды:
Здесь также использовали замену переменных под интегралом.
Использованная литература:
1. Практикум из математического анализа. Часть 2. Заболоцький М. В., Фединяк С. И., Филевич П. В. – Львов: Издательский центр ЛНУ имени Ивана Франко, 2006. – 68 с.
2. Демидович Б. П. Сборник задач и упражнений по математическому анализу. Учебное пособие для студентов физических и механико-математических специальностей ВУЗов.-9-е изд.-М.: Наука, главная редакция физико-математической литературы, 1977. – 528 с.
3. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, том ІІ : – М.: Наука, главная редакция физико-математической литературы, 1966. – 800 с.
4. Справочное пособие по математическому анализу, часть И -К. : “Высшая школа”, 1978. – 696 с.
Площадь
фигуры, ограниченной графиком непрерывной
функции
=
,
(
0),
двумя прямыми
=
,
=
и осью OX
, или площадь криво-линейной трапеции,
ограниченной дугой графика функции
=
,
в (рис.1), вычисляется по формуле :
(1)
рис
1.
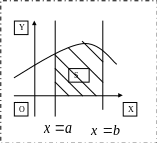
Площадь
фигуры , ограниченной графиками
непрерывных функции
и
и двумя прямыми
=
,
=
(рис.2), определяется по формуле :
(2)
рис.
2
Пример1.
Найти площадь фигуры, лежащей в правой
полуплоскости и ограниченной окружностью
и параболой
Решение:
найдем
точки пересечения кривых ( рис.3), решив
систему уравнений :
рис.
3
Используя
симметрию относительно оси OX
, найдем искомую площадь как удвоенную
сумму площадей криволинейных трапеций
,ограниченных соответственно дугами
параболы
,
0x2
и окружностью.
S=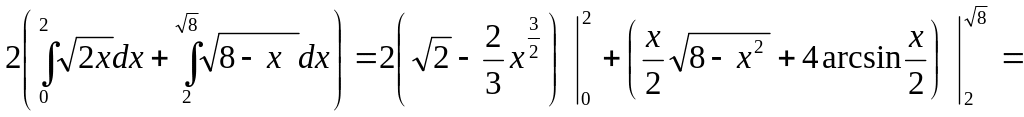
=
Иногда
удобно использовать формулы , аналогичные
(1) и (2) , но по переменной
(считая x
функцией от
),
в частности
(3)
Если
фигура ограничена кривой, имеющей
параметрические уравнения
=
,
=
,
прямыми
=
,
=
и осью OX,
то площадь вычисляется по формуле :
(4),
где
пределы интегрирование находятся из
уравнений
на
отрезке
.
Формула
(4) применима также для вычисления площади
фигуры, ограниченной замкнутой кривой
( изменения параметра t
от
до
должно
соответствовать обходу контура по
часовой стрелке).
Пример2.
Найти площадь петли кривой
Решение:
Найдем точки пересечения кривой с
координатами осями. Имеем : x=0
при t=
;
y=0
при t=0,
t=
.Следовательно,
получаем следующие точки:
при
t=1;
при t=-1;
при
t=0;
при t=
.
Точка
является точкой самопересечения кривой.
При
При
(рис.4).
График
функции
;
,
при
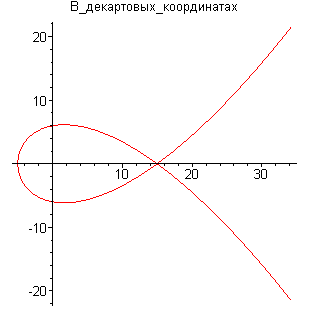
Площадь фигуры
находим как удвоенную площадь верхней
ее половины:
Площадь
фигуры, ограниченной графиком непрерывной
функции
и двумя лучами
где
– полярные координаты, или площадь
криволинейного сектора , ограниченного
дугой графика функции
,
,
вычисляется по формуле:
(5).

Пример
3. Найти площадь лунки , ограниченной
дугами окружностей
Окружности пересекаются при
;
рассматриваемая фигура ( рис.5) симметрична
относительно луча
.
График
функции
;
,
при
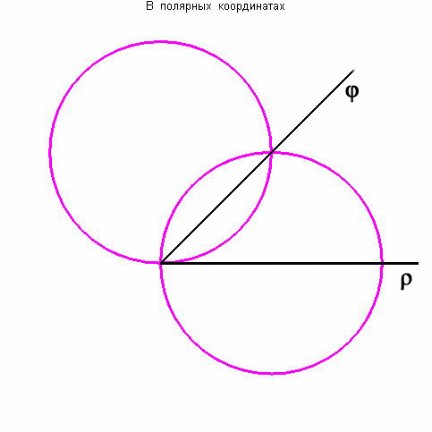
Следовательно,
ее площадь можно вычислять так:
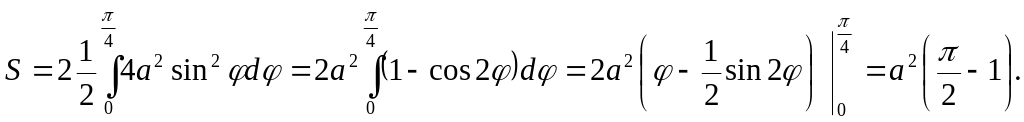
ВАРИАНТЫ
Вычислить
площадь фигуры, ограниченной данными
линиями:
В-1.
-
-
и
ее асимптотой. -
Кардиоидой
. -
.
В-5.
-
-
и
касательные к ней , проведенные через
токи -
одной
аркой циклиды
-
В-3.
-
-
касательной
к ней в точке
и осью OX.
-
Астроидой
-
(
Бернулли ) .
В-4.
-
-
,
касательной к ней в точке x=e
и осью OX. -
Петли
линии
. -
(
улитка Паскаля )
В-5.
-
-
,
касательной к ней в точке
. -
Одной
арки циклоиды
и OX.
-
.
В-6.
-
-
касательной
к ней в точке
и x=1.
-
Петли
линии
-
(кардиоида)
В-7.
-
-
касательной
к ней в точке Mк осью ординат.
-
Петли
кривой
-
(
лепестковая роза).
В-8.
-
Параболой
и гиперболой
-
-
-
(в
не круга
)
В-9
-
-
Найдите
площадь фигуры, ограниченной графиком
функции
и касательными к этому графику,
проведенными через точку
. -
-
В-10
-
-
Найдите
площадь фигуры, ограниченной графиком
функции
и касательными к этому графику,
проведенными через точку
. -
-
В-11
-
-
Найдите
площадь фигуры, ограниченной графиками
функций
,
и осью ординат.
-
-
В-12
2)
3)
4)
В-13
В-14
В-15
В-16
В-17
1)
В-18
1)
В-19
В-20
-
-
-
-
площадь,
ограниченную кардиоидой
и окружностью
.
В-21
В-22
-
-
-
одной
петлей кривой
4)
(общая область)
В-23
В-24
В-25
-
-
Вычислить
площадь, ограниченную параболой
и осью абсцисс.
-
-
Вопросы к
лабораторной работе №9:
-
Какая
фигура называется квадрируемой? Какие
вы знаете условия квадрируемости? -
Какими свойствами
обладает квадрируемая фигура? -
Как
вычисляется площадь плоской фигуры,
ограниченной прямыми
и непрерывными кривыми
и
,
при условии, что
для
?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #