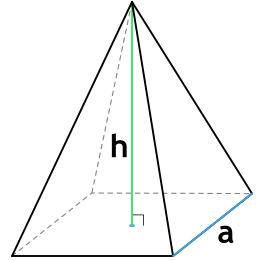
Основание правильной пирамиды является правильный многоугольник – равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды – это площадь этой плоской фигуры.
Площадь основания правильной пирамиды
Правильная пирамида может быть трех видов:
- треугольная,
- четырехугольная,
- шестиугольная.
Соответственно у правильной треугольной пирамида основание – равносторонний треугольник. У правильной четырехугольной пирамиды основание – квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:
Площадь основания правильной треугольной пирамиды
В основании равносторонний треугольник – находим его площадь:
, где
– сторона треугольника.
Площадь основания правильной четырехугольной пирамиды
В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:
, где
– сторона квадрата.
Площадь основания правильной шестиугольной пирамиды
Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:
Площадь основания любой пирамиды
Площадь основания любой пирамиды – это площадь ее основания.
Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье “Площадь треугольника”.
В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.
Теперь давайте решим несколько задач для нахождения площади основания пирамиды
Примеры решения задач
Задача 1
Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.
Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона
, тогда
Ответ:
Задача 2
Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?
Решение:
Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны
. Получим:
м2.
Теперь подсчитаем, сколько нам понадобится досок: .
Ответ: 108 досок.
Задача 3
Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.
Решение: иными словами – нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой – высотой. Определяем площадь по формуле:
.
Ответ: 8
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
- 2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
-
4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
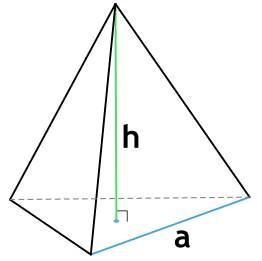
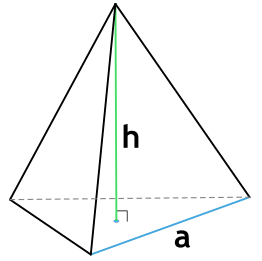
1. Через длину основания (a) и высоту (h):
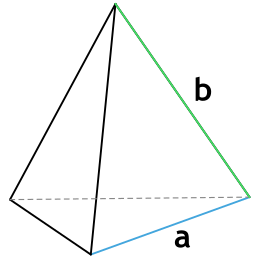
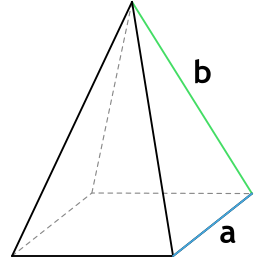
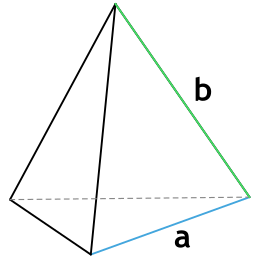
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
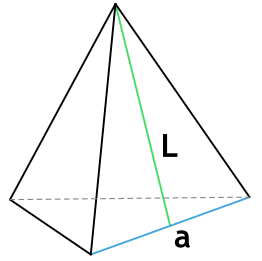
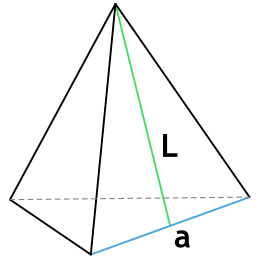
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
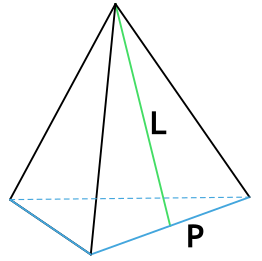
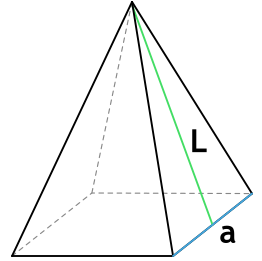
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
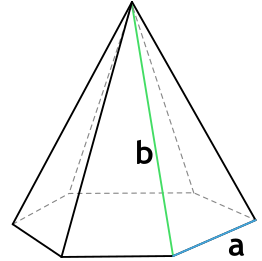
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник
Полная площадь боковой поверхности пирамиды состоит из суммы площадей его боковых граней.
В четырехугольной пирамиде различается два вида граней – четырехугольник в основании и треугольники с общей вершиной, которой образуют боковую поверхность.
Для начала потребуется рассчитать площадь боковых граней. Для этого можно использовать формулы площади треугольника, а можно также воспользоваться формулой площади поверхности четырехугольной пирамиды (только в случае, если многогранник правильный). Если пирамида правильная и в ней известна длина ребра a основания и проведенной к нему апофемы h, то:
Если по условиям даны длина ребра c правильной пирамиды и длина стороны основания a, то можно найти значение по следующей формуле:
Если же дана длина ребра в основании и противолежащий ей острый угол у вершины, то можно рассчитать площадь боковой поверхности по соотношению квадрата стороны a к удвоенному косинусу половины угла α:
Рассмотрим пример расчета площади поверхности четырехугольной пирамиды через боковое ребро и сторону основания.
Задача: пусть дана правильная четырехугольная пирамида. Длина ребра b = 7 см, длина стороны основания a = 4 см. Подставим заданные значения в формулу:
Мы показали расчеты площади одной боковой грани для правильной пирамиды. Соответственно. Чтобы найти площадь всей поверхности необходимо умножить результат на количество граней, то есть на 4. Если пирамида произвольная и ее грани не равны между собой, то рассчитать площадь необходимо для каждой отдельной стороны. Если в основании лежит прямоугольник или параллелограмм, то стоит вспомнить их свойства. Стороны у этих фигур попарно параллельны, а соответственно грани пирамиды будут также попарно одинаковы.
Формула площади основания четырехугольной пирамиды напрямую зависит от того, какой четырехугольник лежит в основании. Если пирамида правильная, то площадь основания рассчитывается по формуле площади квадрата, если в основании лежит ромб, то потребуется вспомнить, как находится площадь ромба. Ели же в основании лежит прямоугольник, то найти его площадь будет довольно просто. Достаточно знать длины сторон основания. Рассмотрим пример расчета площади основания четырехугольной пирамиды.
Задача: Пусть дана пирамида, в основании которой лежит прямоугольник со сторонами a = 3 см, b = 5 см. К каждой из сторон из вершины пирамиды опущена апофема. h-a=4 см,h-b=6 см. Вершина пирамиды лежит на одной линии с точкой пересечения диагоналей. Найдите полную площадь пирамиды.
Формула площади четырехугольной пирамиды состоит из суммы площадей всех граней и площади основания. Для начала найдем площадь основания:
Теперь рассмотрим грани пирамиды. Они попарно одинаковы, потому что высота пирамиды пересекает точку пересечения диагоналей. То есть, в нашей пирамиде есть два треугольника с основанием a и высотой h-a, а также два треугольника с основанием b и высотой h-b. Теперь найдем площадь треугольника по известной формуле:
Теперь выполним пример расчета площади четырехугольной пирамиды. В нашей пирамиде с прямоугольником в основании, формула будет выглядеть так:

{S_{полн} = dfrac{1}{2}PL + S}
На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды – это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды – это совокупная площадь всех боковых граней пирамиды.
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
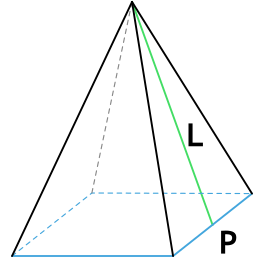
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
{S_{полн} = dfrac{1}{2}PL+S}
P – периметр основания пирамиды
L – апофема пирамиды
S – площадь основания пирамиды
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{na}{2} {Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} + sqrt{h^2+ Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
n – число сторон основания
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{a^2 sqrt{3}+6aL}{4}}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{a^2 sqrt{3}+6a sqrt{b^2 – dfrac{a^2}{4}}}{4}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{3a}{2} {Bigg( dfrac{a}{2 tg ( 60°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{полн} = 2a {Bigg( dfrac{a}{2 tg ( 45°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{полн} = a^2+2aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3asqrt{b^2-dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{полн} = 3a {Bigg( dfrac{a}{2 tg ( 30°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
{S_{бок} = dfrac{1}{2}PL}
P – периметр основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{na}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( dfrac{180°}{n})} Bigg) ^2} }
a – сторона основания пирамиды
h – высота пирамиды
n – число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{бок} = dfrac{3}{2}aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{бок} = dfrac{3a sqrt{b^2 – dfrac{a^2}{4}}}{2}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{3a}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
{S_{бок} =dfrac{1}{2}PL}
P – периметр основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{бок} = 2aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 2a sqrt{b^2 – dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{бок} = 3aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 3asqrt{b^2-dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{бок} = 3a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. Найдите площадь поверхности этой пирамиды.
Решение
Так как пирамида правильная четырехугольная, то воспользуемся соответствующей формулой площади поверхности через сторону основания и боковую грань.
S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}} = 60^2 + 2 cdot 60 sqrt{78^2- dfrac{60^2}{4}} = 3600 + 120 sqrt{6084- dfrac{3600}{4}} = 3600 + 120 sqrt{6084 – 900} = 3600 + 120 sqrt{5184} = 3600 + 120 cdot 72 = 3600 + 8640 = 12240 : см²
Ответ: 12240 см²
Проверим полученный ответ с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной треугольной пирамиды со стороной 6см и апофемой 10см.
Решение
Из условия мы знаем апофему и сторону правильной треугольной пирамиды, поэтому нам потребуется эта формула.
S_{бок} = dfrac{3}{2}aL = dfrac{3}{2} cdot 6 cdot 10 = dfrac{3}{2} cdot 60 = 90 : см²
Ответ: 90 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной четырехугольной пирамиды сторона основания 6см и высота 4см.
Решение
Подставим значения в формулу и произведем расчет.
S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} = 2 cdot 6 sqrt{4^2+ Bigg( dfrac{6}{2 tg ( 45°)} Bigg) ^2} = 60 : см²
Ответ: 60 см²
Проверка .
Площадь правильной четырехугольной пирамиды
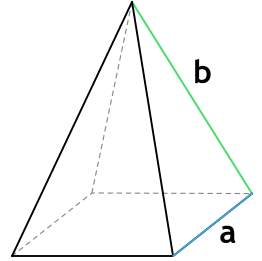
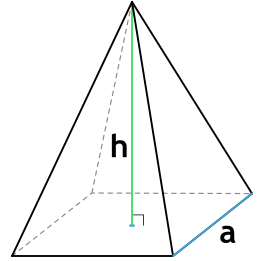
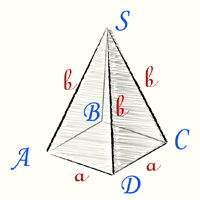
Основанием правильной четырехугольной пирамиды является квадрат со стороной a, боковыми гранями являются четыре равнобедренных треугольника с основанием a и равными бедрами b.
Площадь правильной четырехугольной пирамиды равна сумме площадей основания — квадрата пирамиды и площади четырех треугольников боковых граней.
[ S = S_{осн} + 4 S_{бок} ]
Раскроем формулу (1) подставив в нее площадь квадрата и площадь равнобедренных треугольников
[ S = a^2 + 2 a sqrt{b^2-frac{a^2}{4}} ]
Вычислить, найти площадь правильной четырехугольной пирамиды
Площадь правильной четырехугольной пирамиды |
стр. 325 |
|---|