Как найти площадь основания цилиндра зная радиус

В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.

Формула вычисления площади цилиндра

1. Боковая поверхность

Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.

Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:

S = 2 π R h

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:

S = π R²

Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:

S = π (d/2)²

3. Полная площадь

Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:

S = 2 π R h + 2 π R² или S = 2 π R (h + R)

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см².

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см)  = 326,56 см².

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Онлайн калькулятор для цилиндра позволяет по известным данным вычислить:

• объем цилиндра,
• площадь основания, площадь боковой поверхности и  площадь полной поверхности цилиндра,
• элементы: радиус, диаметр и высоту.

Калькулятор для цилиндра: комментарий

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).

Обозначения для цилиндра:
R – радиус, D – диаметр,
V – объем,
Sо – площадь основания, Sб – площадь боковой поверхности, S – площадь полной поверхности,
h – высота прямого кругового цилиндра (h1 и h2 — минимальная  и максимальная высота)
π – число Пи которое всегда примерно равно 3,14.

Прямой круговой цилиндр

Круговым называется цилиндр, если его направляющая является окружностью. Прямым называется цилиндр, если его образующая перпендикулярна основаниям.

Формулы для прямого кругового цилиндра:

Найти объем цилиндра, если известны:

• радиус и высота цилиндра: V=πR²h
• диаметр и высота цилиндра: V=πD²/4h
• площадь и высота цилиндра: V=Sоh

Площадь(Sб) боковой поверхности прямого кругового цилиндра

Так как боковая поверхность представляет собой прямоугольник, то площадь боковой поверхности цилиндра определяется по формуле: Sб=2πR⋅h

Площадь(Sо) основания цилиндра

Основание цилиндра —круг, поэтому площадь одного основания находится по формуле площади круга: Sо=πR².

Площадь(S)  полной поверхности прямого кругового цилиндра

Площадь полной поверхности цилиндра определяется по формуле: S=2πRh+2πR²=2πR(h+R)

Формулы нахождения радиуса и диаметра по:

• высоте и объему: R=√(V/πh), D=2*√(V/πh)
• площади боковой поверхности и высоте: R=Sб/2πh, D=2*Sб/2πh
• площади основания и высоте: R=√(Sо/π), R=2*√(Sо/π)

Формулы нахождения высоты по:

• радиусу и объему: h=V/πR²
• площади боковой поверхности и радиусу: h=Sб/2πR
• площади полной поверхности и радиусу: h=S/2πR-R

Скошенный цилиндр

Прямой круговой цилиндр со скошенным основанием (скошенный цилиндр) определяется радиусом основания R, минимальной высотой h1 и максимальной высотой h2.

Формулы для скошенного цилиндра:

• Объем скошенного цилиндра: V=πR²(h1+h2)²
• Площадь(Sб) боковой поверхности скошенного цилиндра: Sб=πR(h1+h2)
• Площадь(Sо) оснований скошенного цилиндра: Sо=πR²+πR √(R2+((h1−h2)/2)²)
• Площадь(S) полной поверхности скошенного цилиндра  
  S=Sб+Sо= πR(h1+h2)+ πR²+πR √ (R²+((h1−h2)/2)²)  = πR[(h1+h2)+ R+√ (R²+((h1−h2)/2)²) ]

Список всех онлайн-конвертеров на странице «Калькуляторы«.

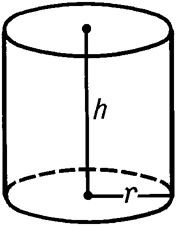
Цилиндр – это геометрическая фигура, полученная вращением прямоугольника вокруг одной из его сторон. У каждого цилиндра есть 2 одинаковых основания (верхнее и нижнее) и боковая поверхность.

Любой цилиндр характеризуется высотой h (осевой линией) и радиусом r (см. рисунок). Именно эти характеристики используются в формулах цилиндра при вычислении объема, площади поверхности и площади боковой поверхности.

Высота цилиндра (осевая линия) – это перпендикуляр, проведенный от верхнего основания к нижнему.

Радиус цилиндра – это радиус его основания.

Формула площади боковой поверхности цилиндра

Площадь боковой поверхности цилиндра можно получить, зная его высоту H и длину основания L:

S_{бок.пов} = LH = 2πrH

Формула площади основания цилиндра

Площадь основания цилиндра можно вычислить по его радиусу R:

S_осн = πR²

Формула площади цилиндра

Площадь поверхности цилиндра можно получить, сложив площадь боковой поверхности и 2 площади основания цилиндра:

S = S_{бок.пов} + 2S_осн = 2πRH + 2πR²

Формула объема цилиндра

Объем цилиндра можно вычислить, зная его высоту H и площадь основания:

V = S_осн ⋅ H = πR²H