Так как площадь основания конуса зависит только от радиуса, следовательно, зная ее, можно сразу вычислить радиус конуса и диаметр и периметр основания.
r=√(S_(осн.)/π)
d=2√(S_(осн.)/π)
P=2πr=2√(πS_(осн.) )
Если построить прямоугольный треугольник, соединяющий образующую конуса с высотой через радиус, то, зная образующую и радиус, можно вычислить высоту по теореме Пифагора, а также угол наклона конуса между образующей и основанием. Далее, через равнобедренный треугольник с образующими и диаметром, можно найти угол раствора конуса, как разность двух углов наклона от 180 градусов. (рис.40.1,40.2)
h=√(l^2-r^2 )=√(l^2-S_(осн.)/π)
cosβ=r/l
α=180°-2β
Чтобы найти площадь боковой поверхности понадобится радиус и образующая конуса, а если затем прибавить к полученному выражению данную по условию площадь основания, то получится площадь полной поверхности конуса.
S_(б.п.)=πrl=l√(πS_(осн.) )
S_(п.п.)=S_(осн.)+l√(πS_(осн.) )
Объем конуса рассчитывается через площадь основания и высоту, заменив высоту на квадратный корень из квадрата образующей за вычетом площади основания, деленной на число π, получим формулу объема через площадь основания и образующую.
V=1/3 hS_(осн.)=S_(осн.)/3 √(l^2-S_(осн.)/π)
Вычислить радиусы сфер вписанной и описанной около конуса через площадь основания и образующую, можно используя нижеприведенные формулы. (рис. 40.3, 40.4)
r_1=hr/(l+r)=√((l^2-S_(осн.)/π)(S_(осн.)/π) )/(l+√(S_(осн.)/π))
R=l^2/2h=l^2/(2√(l^2-S_(осн.)/π))
Как рассчитать площадь поверхности конуса
На данной странице калькулятор поможет рассчитать площадь поверхности конуса онлайн. Для расчета задайте высоту, радиус или образующую.
Конус – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.
Образующая конуса – это отрезок, соединяющий вершину и границу основания.
Боковая поверхность через радиус и образующую
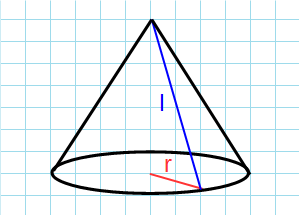
Формула боковой поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Боковая поверхность через радиус и высоту
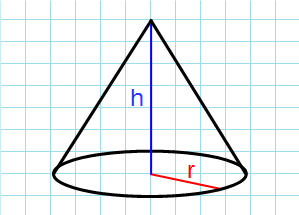
Формула боковой поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Полная площадь через радиус и образующую

Формула площади полной поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Полная площадь через радиус и высоту

Формула полной площади поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Площадь поверхности конуса онлайн калькулятор
Онлайн калькулятор площади поверхности конуса вычислит площадь различными формулами.
Возможно два варианта расчета – либо площадь всей поверхности, – либо только боковой поверхности.
Сделав расчет площади конуса на этом калькуляторе Вы не только получите ответ но и детальное пошаговое решение с выводом формул.
- Калькулятор
- Инструкция
- Теория
- История
- Сообщить о проблеме

Что необходимо найти:
Радиус R:
Образующая L:
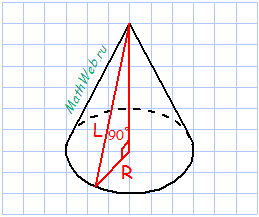
Конус – это геометрическая фигура, которая получается путем вращения прямоугольного треугольника вокруг его катета.
Формула площади всей поверхности конуса 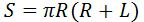
где R – радиус вращения, L – длина образующей.
Решение:
S = π·R·(R+L)
S = π·6.7·(6.7+6.75)
S = π·6.7·13.45
= 90.115·π
=
283.096
Ответ: Площадь всей поверхности конуса с радиусом R = 6.7, и образующей L = 6.75 равна 283.096
Образующая конуса — это линия соединяющая вершину конуса с его основанием.
Высота конуса — это линия соединяющая вершину конуса с центром его основания.
Боковая поверхность конуса — это поверхность получаемая слиянием всех образующих.
Площадь всей поверхности конуса — это сумма площади боковой поверхности и площади основания.
Скачать все формулы нахождения площади поверхности конуса в формате Word/PDF
Похожие калькуляторы
-
Площадь поверхности призмы онлайн калькулятор
-
Площадь поверхности параллелепипеда онлайн калькулятор
-
Площадь боковой поверхности цилиндра онлайн калькулятор (2 способа)
-
Площадь поверхности цилиндра онлайн калькулятор (2 способа)
-
Площадь поверхности шара онлайн калькулятор (2 способа)
Калькуляторы других категорий
-
Деление в столбик онлайн. Калькулятор наглядного деления.
-
Перевод чисел из одной системы счисления в любую другую онлайн
-
Сторона треугольника 14 формул расчет онлайн
-
Сложение, умножение и деление чисел в различных системах счисления
-
Умножение в столбик онлайн. Калькулятор наглядного умножения.
| Ваша оценка? |
Расчет приведен для прямого кругового конуса (подробное описание внизу страницы)
Площадь основания конуса равна:
Площадь боковой поверхности конуса равна:
Полная площадь конуса равна:
Как рассчитать площадь поверхности прямого кругового конуса по радиусу основания и его высоте?
Площадь поверхности прямого кругового конуса равна сумме площадей основания конуса и боковой поверхности конуса.
Прямой круговой конус — конус в основании которого лежит круг и центр симметрии совпадает с центром этого круга (то есть это обычный, в простом понимании, конус).
Площадь основания конуса определяется по формуле:
Sо = Π*r2
Площадь боковой поверхности конуса, если известна высота, определяется по формуле:
Sб = П*r*(√(r2+h2))
Полная площадь поверхности конуса равна:
Sп = Sо + Sб = Π*r2 + П*r*(√(r2+h2)), где
h — высота конуса;
Π = 3.1415926535 — математическая постоянная, равная отношению длины окружности к её диаметру;
r — радиус основания конуса.
Полная площадь поверхности конуса равна сумме площадей основания конуса и боковой поверхности конуса.
Если радиус и высота конуса измерены в см (сантиметрах), то площадь конуса равна:
Sсм2(п) = Π*rсм2 + П*rсм*(√(rсм2+hсм2))
Sм2(п) = (Π*r2см + П*rсм*(√(rсм2+hсм2)))/10 000
Площадь конуса вычисляется путем суммирования значений S лежащего в основании круга и S боковой поверхности фигуры. Исходными данными для ее вычисления является радиус R и образующая l, площадь конуса вычисляется по формуле S = π х R х (R + l).
Образующая боковой поверхности l – отрезок, соединяющий вершину конуса и любую точку базисной окружности основания данной геометрической фигуры. Калькулятор вычисляет площадь конуса после внесения исходных данных в соответствующие поля формы на странице и нажатия кнопки «Вычислить».
Конус является одной из элементарных объемных геометрических фигур, из которых состоят сложные детали различных инженерных сооружений и конструкций. Конструкторам и проектировщикам в их работе довольно часто требуется вычислять S конуса.
Потребность в расчете площади конуса может быть необходима для последующего выяснения значений важных показателей эксплуатационных нагрузочных и прочностных характеристик, приходящихся на единицу площади фигуры. С учетом S конуса выбирается соответствующий исходный материал, из которого будет изготовлена проектируемая деталь.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»








