Как найти площадь основания куба 5 класс

На этой странице вы найдете ответ на вопрос Как найти площадь основания куба?. Вопрос
соответствует категории Математика и уровню подготовки учащихся 1 – 4 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.

Площадь поверхности куба, формулы и примеры

Формулы для нахождения площади поверхности куба:

1. Через длину грани H: S=6*H^2
2. Через длину диагонали d: S =6*H^2=6*(frac < d >< sqrt < 3 >> )

Как найти площадь поверхности куба?

1. Чтобы найти с гранью H, надо сложить сумму площадей всех его граней, то есть вычислить площадь квадрата со стороной H, и умножить полученный результат на 6.
   S=6*H
2. Если известна только диагональ грани куба, надо его диагональ d поделить на квадратный корень из трёх и результат умножить на 6.
   S =6*(frac < d >< sqrt < 3 >> )

Примеры

1. Дан куб с ребром H = 7. Для начала возведем длину его грани в квадрат:
   H 2 = H * H = 7 * 7 = 49. Мы получили периметр одной грани.
   Для вычисления площади результат из первого действия умножим на количество граней:
   S = 6 * 49 = 294.
   Мы получили искомый результат.
   Ответ: 294.
2. Дан куб с диагональю ребра d=13. Требуется найти площадь его поверхности
   Вычислим его грань H, исходя из формулы H=frac < d >< sqrt < 3 >> = frac < 13 >< sqrt < 3 >> = 7,51.
   Теперь, когда нам известна величина грани куба, воспользуемся первой формулой, и умножим результат на 6 :
   S = 6 * H 2 = 6 * 7,512 2 = 6 * 56,43 ≈ 338.
   Мы снова получили искомый результат.
   Ответ: 338.

Площадь поверхности прямоугольного параллелепипеда равна

S_{пов. куба} = (аа + аа +аа) * 2 = 6 а 2

S_{пов. куба} = 6 а 2

Пример. Площадь поверхности куба равна 18. Найдите его диагональ.

S_{пов. куба} = 6 а 2

Источник

Все формулы для площадей полной и боковой поверхности тел

1. Площадь полной поверхности куба

a — сторона куба

Формула площади поверхности куба,(S):

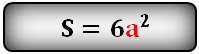
2. Найти площадь поверхности прямоугольного параллелепипеда

a , b , c — стороны параллелепипеда

Формула площади поверхности параллелепипеда, (S):

3. Найти площадь поверхности шара, сферы

R — радиус сферы

Формула площади поверхности шара (S):

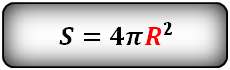
4. Найти площадь боковой и полной поверхности цилиндра

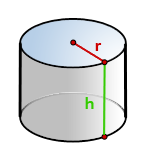
r — радиус основания

h — высота цилиндра

Формула площади боковой поверхности цилиндра, (S _бок ):

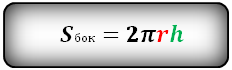
Формула площади всей поверхности цилиндра, (S):

5. Площадь поверхности прямого, кругового конуса

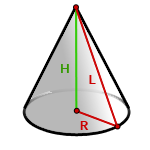
R — радиус основания конуса

L — образующая конуса

Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S _бок ):

Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S _бок ):

Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):

Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):

Источник

Нахождение площади поверхности куба: формула и задачи

В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.

Формула вычисления площади куба

1. Через длину ребра

Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.

Данная формула получена следующим образом:

Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).

2. Через длину диагонали грани

Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√ 2 .

Это значит, что вычислить площадь поверхности фигуры можно так:

S = 6 ⋅ (d/√ 2 ) 2

Примеры задач

Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.

Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см) 2 = 864 см 2 .

Задание 2
Площадь поверхности куба равняется 294 см 2 . Вычислите длину его ребра.

Решение:
Примем ребро куба за a. Из формулы расчета площади следует:

Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.

Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √ 2 ) 2 = 75 см 2 .

Источник

Что такое куб: определение, свойства, формулы

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:

Свойство 2

Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

• a – ребро куба;
• d – диагональ куба или его грани.

Диагональ

Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.

Диагональ грани

Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

Периметр ребер

Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.

Объем

Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара

Радиус шара, описанного около куба, равняется половине его диагонали.

Радиус вписанного шара

Радиус вписанного в куб шара равен половине длины его ребра.

Источник

Площадь поверхности куба.

Площадь поверхности куба – это суммарная площадь всех поверхностей фигуры. Площадь поверхности куба равна сумме площадей всех его шести граней. Площадь поверхности является числовой характеристикой поверхности. Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.

Определение площади поверхности куба.

Определение площади поверхности куба выполняется по формуле SA = 6а 2 . Куб (правильный гексаэдр) — это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.

Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а 2 . Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять — a 2 , где а – сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а – ребро куба (сторона квадрата).

Чему равна площадь поверхности куба.

Площадь поверхности куба измеряется в квадратных единицах, к примеру, в мм 2 , см 2 , м 2 и так далее. Для дальнейших расчетов Вам необходимо будет измерить ребро куба. Как мы знаем, ребра у куба равны, поэтому Вам будет достаточно измерить только одно (любое) ребро куба. Выполнить такой замер Вы можете при помощи линейки (или рулетки). Обратите внимание на единицы измерения на линейке или рулетке и запишите значение, обозначив его через а.

Полученное значение возведите в квадрат. Таким образом, Вы возведите в квадрат длину ребра куба. Для того чтобы возвести число в квадрат умножьте его на себя. Наша формула будет иметь следующий вид: SA = 6*а 2

Вы вычислили значение площади одной из граней куба.

Полученное значение умножайте на шесть. Не забывайте, что у куба 6 равных граней. Определив площадь одной из граней, умножьте полученное значение на 6, чтобы все грани куба участвовали в расчете.

Вот мы и пришли к конечному действию по вычислению площади поверхности куба.

Источник

Площадь поверхности куба

Онлайн калькулятор

Чему равна площадь поверхности куба, если:

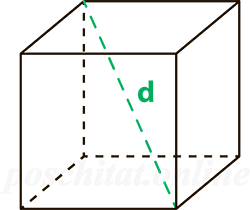Чему равна площадь поверхности куба, если:

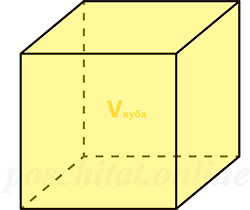Чему равна площадь поверхности куба, если:

Теория

Площадь поверхности куба через ребро

Чему равна площадь поверхности куба S_пов, если длина его ребра a:

Формула

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если он имеет длину рёбер a = 5 см :

Площадь поверхности куба через диагональ

Чему равна площадь поверхности куба S_пов, если длина диагонали этого куба d:

Формула

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если длина диагонали у него d = 3 м:

S_пов = 2 ⋅ 3² = 2 ⋅ 9 = 18 м² = 180 000 см²

Площадь поверхности куба через объем

Чему равна площадь поверхности куба S_пов, если объём куба V_куба:

Формула

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если его объём V_куба = 8 см³:

S_пов = 6 ⋅ 3 √ 8² = 6 ⋅ 3 √ 64 = 6 ⋅ 4 = 24 см²

Источник

Формулы площади поверхности геометрических фигур

Площадь куба

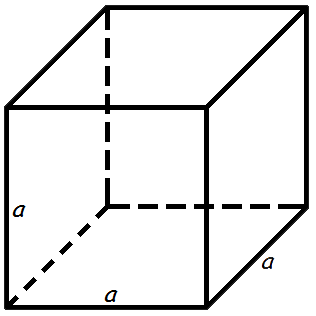
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.

Площадь прямоугольного параллелепипеда

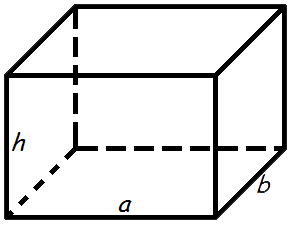
Формула площади поверхности прямоугольного параллелепипеда:

Площадь цилиндра

Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.

Формула для вычисления площади боковой поверхности цилиндра:

Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.

Формула для вычисления площади полной поверхности цилиндра:

Площадь конуса

Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число π .

Формула площади боковой поверхности конуса:

Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.

Формула площади полной поверхности конуса:

Площадь шара

Площадь поверхности шара равна четырем его радиусам в квадрате умноженным на число π .

Площадь поверхности шара равна квадрату его диаметра умноженного на число π .

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.

• Формула вычисления площади куба
  • 1. Через длину ребра
  • 2. Через длину диагонали грани

• Примеры задач

Формула вычисления площади куба

1. Через длину ребра

Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.

S = 6 ⋅ a²

Данная формула получена следующим образом:

• Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
• Площадь каждой грани считается так: S = a ⋅ a = a².
• Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a².

2. Через длину диагонали грани

Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.

Это значит, что вычислить площадь поверхности фигуры можно так:

S = 6 ⋅ (d/√2)²

Примеры задач

Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.

Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см)² = 864 см².

Задание 2
Площадь поверхности куба равняется 294 см². Вычислите длину его ребра.

Решение:
Примем ребро куба за a. Из формулы расчета площади следует:

Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.

Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √2)² = 75 см².

In geometry, the bottom of a three-dimensional object is called a base – if the top of the solid is parallel to the bottom it is also called a base. Since bases occupy a single plane, they have only two dimensions. You can find the area of a base by using the formula for the area of that shape.

Square Bases

Cubes and square pyramids have bases that are square-shaped. The area of a square is equal to the length of one of its sides multiplied by itself, or squared. The formula is A = s². For example, to find the area of a base of a cube with 5-inch sides: A = 5 inches x 5 inches = 25 square inches

Rectangular Bases

Some rectangular solids and pyramids have rectangular bases. The area of a rectangle is equal to its length, l, multiplied by its width, w: A = l x w. Given a pyramid whose base is 10 inches long and 15 inches wide, find area as follows: A = 10 inches x 15 inches = 150 square inches.

Circular Bases

The bases of cylinders and cones are circular. The area of a circle is equal to the circle’s radius, r, squared then multiplied by a constant called pi: A = pi x r². Pi always has the same value, approximately 3.14. While pi technically has an endless number of decimal places, 3.14 is a good enough estimation for simple calculations. For example, given a cylinder with a radius of 2 inches, you can find the base’s area as follows: A = 3.14 x 2 inches x 2 inches = 12.56 square inches.

Triangular Bases

A triangular prism has a triangular base. Finding a triangle’s area requires two known quantities: base, labeled b, and height, labeled h. Base is the length of one of the triangle’s sides, height is the distance from that side to the opposite corner of the triangle. The area of the triangle is equal to half of the base times the height: A = b x h x 1/2 You could find the area of a triangle with base length of 4 inches and height of 3 inches as follows: A = 4 inches x 3 inches x 1/2 = 6 square inches.