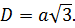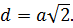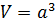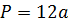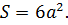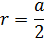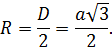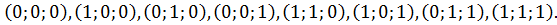Как найти площадь основания куба формула

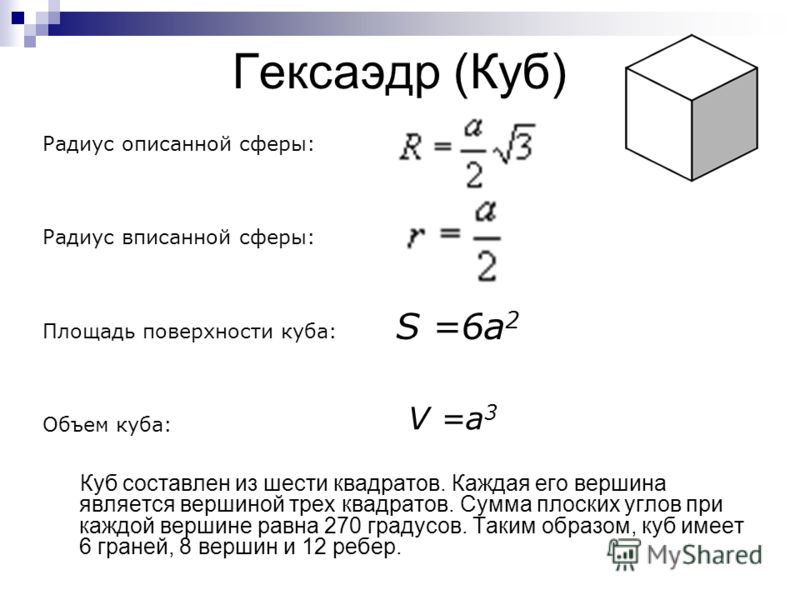
Куб. Формулы, признаки и свойства

Навигация по странице:
Определение куба
Грань куба
Ребро куба
Вершина куба
Центр грани куба
Центр куба
Ось куба
Диагональ куба
Диагональ грани куба
Объём куба
Площадь поверхности куба
Периметр куба
Сфера вписана в куб
Сфера описана вокруг куба
Свойства куба
Координати вершин куба
Единичный куб
Пересечение единичного куба плоскостью

Определение.

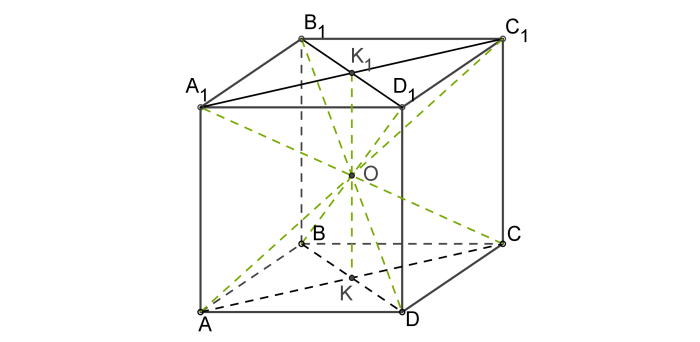
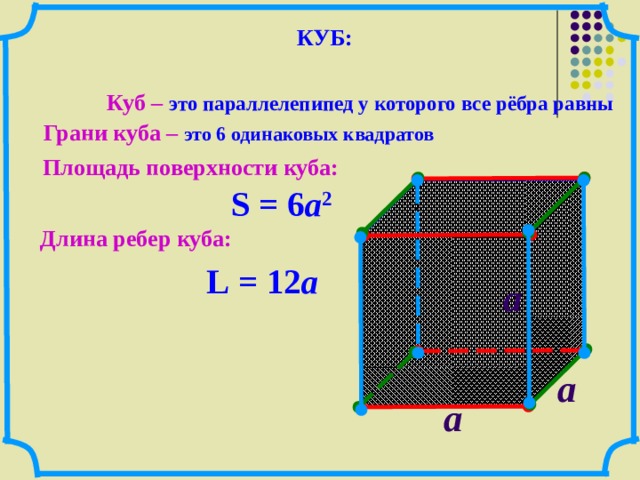
Куб (гексаедр) — это трехмерная фигура, которая состоит из шести динаковых квадратов так, что каждый квадрат полностью соприкасается своими четырьмя сторонами к сторонам остальных четырех квадратов под прямым углом. Куб является правильным многогранником, у которого грани образованы из квадратов. Также кубом можно назвать прямоугольный параллелепипед, у которого все ребра равны.

Определение. Грань куба — это часть плоскости, ограниченная сторонами квадрата.

— куб имеет шесть граней;

— каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани;

— грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.

Определение. Ребро куба — это отрезок, образованный пересечением двух граней куба.

— куб имеет двенадцать ребер;

— каждый конец ребра соединен с двумя соседними ребрами под прямым углом;

— ребра куба имеют одинаковую длину.

Определение. Вершина куба — это самая отдаленная от центра куба точка, которая лежит на пересечения трех граней куба.

— куб имеет восемь вершин;

— каждая вершина образована только тремя гранями и тремя ребрами.

Определение. Центр грани куба (O₁) — это равноудалена точка от всех ребер грани куба.

Определение. Центр куба (O) — это равноудалена точка от всех граней куба.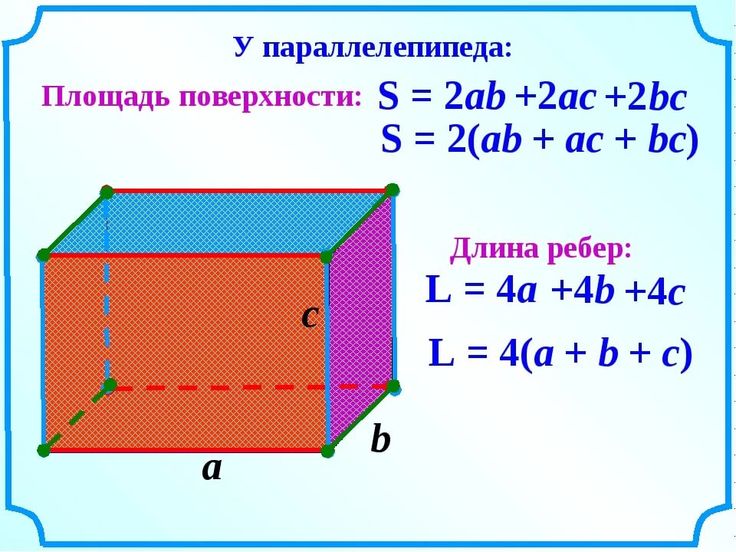

Определение. Ось куба (i) — это прямая, проходящая через центр куба и центры двух параллельных граней куба.

— куб имеет три оси;

— оси куба взаимно перпендикулярны.

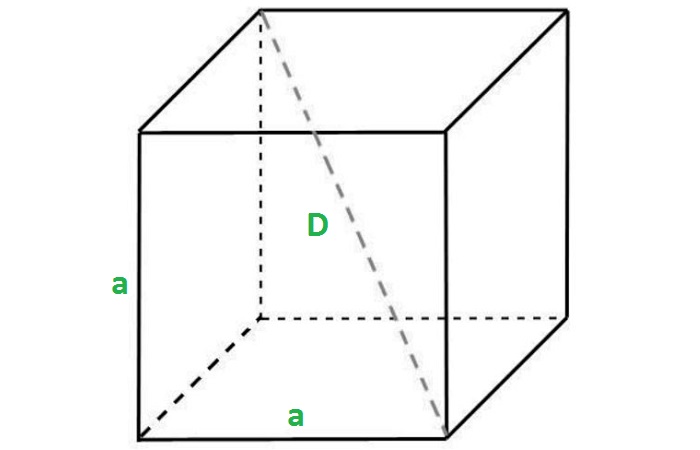
Определение. Диагональ куба (d₁) — отрезок, который соединяет противоположные вершины куба и проходит через центр куба.

— куб имеет четыре диагонали;

— диагонали куба пересекаются и делятся пополам в центре куба;

— диагонали куба имеют одинаковую длину.

Формула. Диагональ куба d₁ через длину ребра a:

d₁ = a√3

Определение. Диагональ грани куба (d₂) -отрезок, который соединяет противоположные углы грани куба и проходит через центр грани куба.

Формула. Диагональ грани d₂ через длину ребра a:

d₂ = a√2

Определение. Объём куба — это совокупность всех точек в пространстве, ограниченные гранями куба.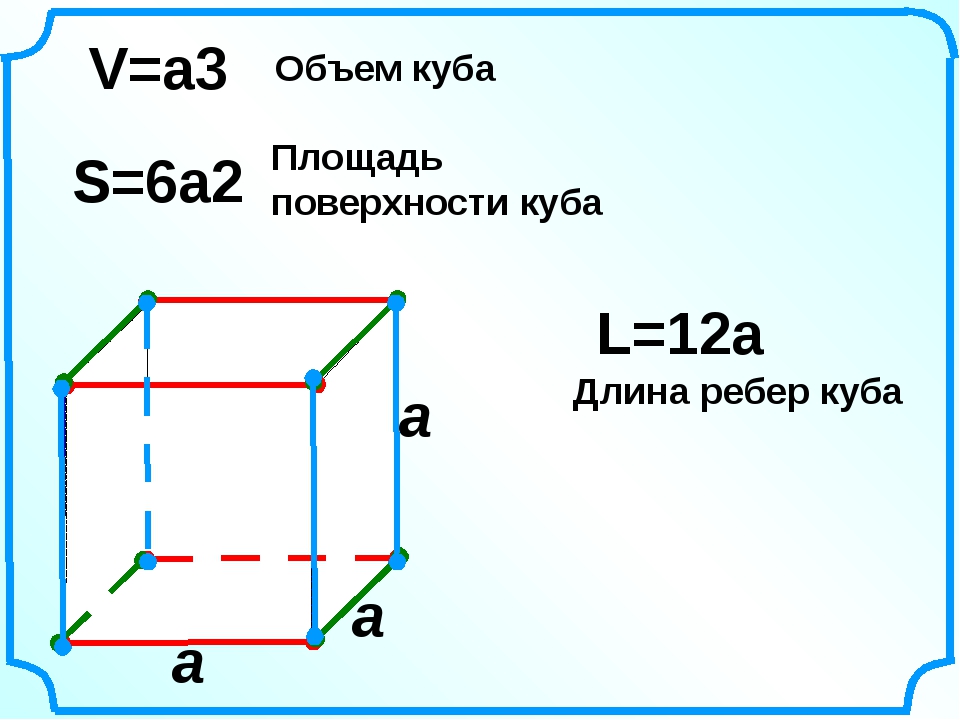

Формула. Объём куба через длину ребра a:

V = a³

Формула. Объём куба через длину диагонали куба d₁:

Определение. Площадь поверхности куба — это совокупность плоскостей всех граней.

Формула. Площадь поверхности куба через длину ребра a:

S = 6a²

Определение. Периметр куба — это совокупность длин всех ребер куба.

Формула. Периметр куба P через длину ребра a:

P = 12a

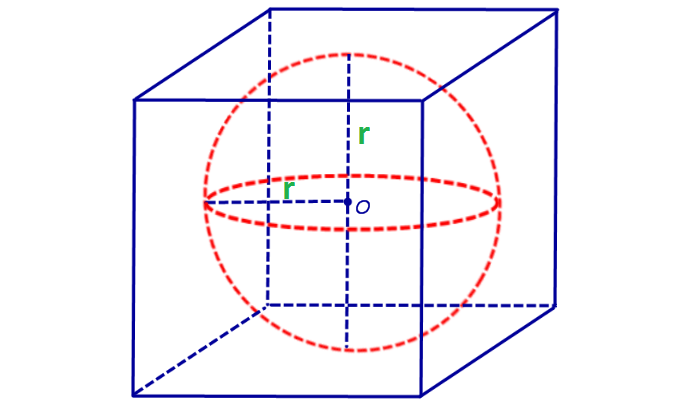
Определение. Сферой вписанной в куб называется сфера, центр которой совпадает с центром куба и которая касается центров граней куба.

— все шесть граней куба являются касательными плоскостями к вписанной сферы;

— радиус вписанной сферы равен половине длины ребра a.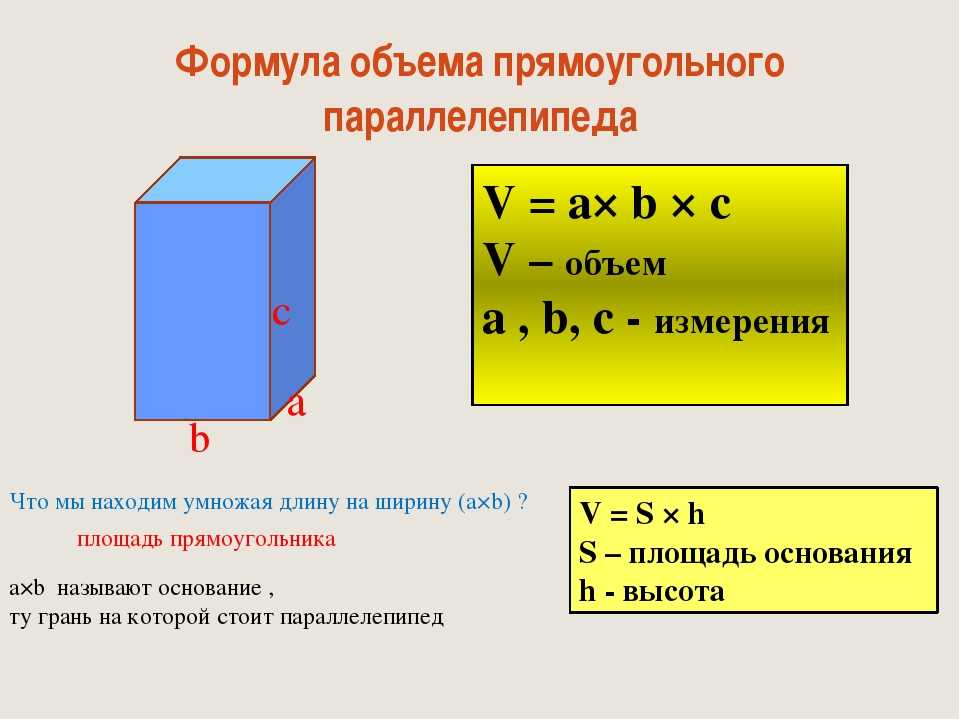

Формула. Радиус вписанной сферы r через длину ребра a:

Формула. Объема вписанной сферы V через длину ребра a:

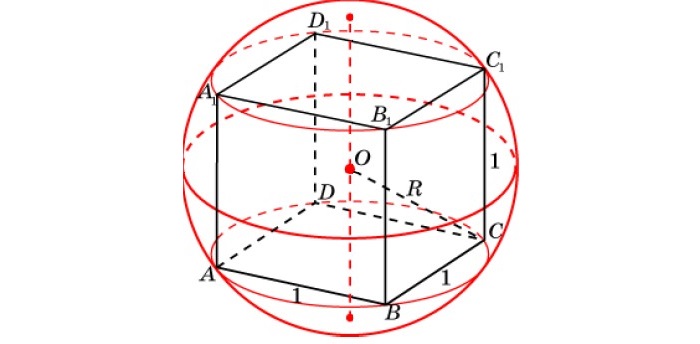
Определение. Сферой описанной вокруг куба называется сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами куба.

— радиус описанной сферы равен половине длины диагонали (d₁) куба.

Формула. Радиус описанной сферы R через длину ребра a:

Формула. Объема сферы описанной вокруг куба V через длину ребра a:

Свойства куба

1. В куб можно вписать тетраэдр так, чтобы все четыре вершины тетраэдра лежали на четырех вершинах куба, а все шесть ребер тетраэдра будут лежать на шести гранях куба и ребра будут равны диагонали грани куба.

2. В куб можно вписать правильный шестиугольник так, что все шесть вершин лежат в центрах граней куба.

Координаты вершин куба

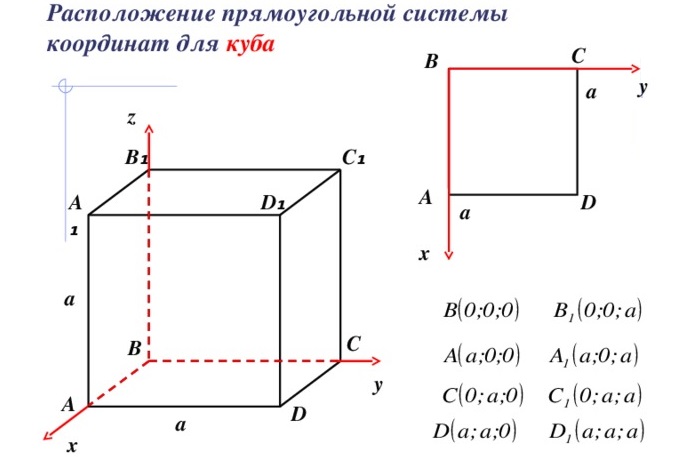
1. Координаты вершин куба со стороной a и вершиной D в начале декартовой системы координат так, что ребра этой вершины лежат на осях координат:

A(a, 0, 0),
B(a, a, 0),
C(0, a, 0),
D(0, 0, 0),
E(a, 0, a),
F(a, a, a),
G(0, a, a),
H(0, 0, a).

2. Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что ребра куба параллельны осям координат:

A(a, -a, -a),
B(a, a, -a),
C(-a, a, -a),
D(-a, -a, -a),
E(a, -a, a),
F(a, a, a),
G(-a, a, a),
H(-a, -a, a).

Определение.

Единичный куб — это куб, у которого длина ребер равна единице.

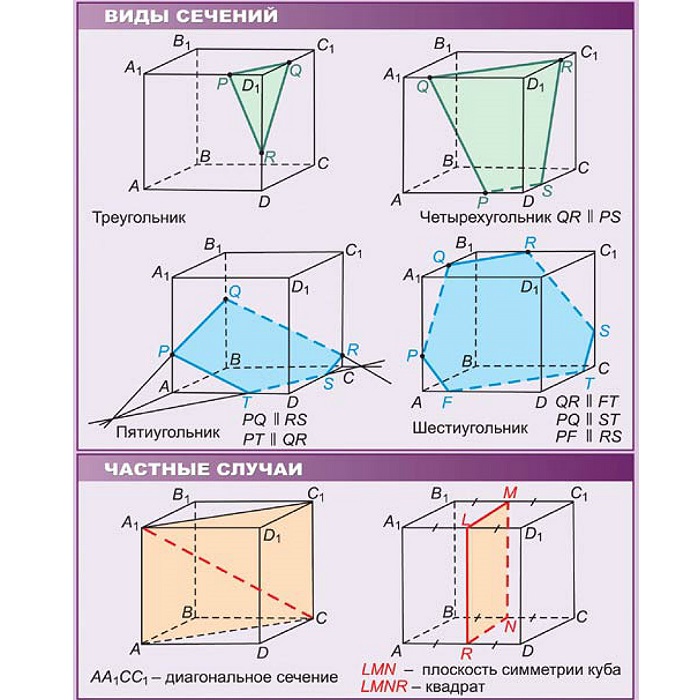
Пересечение куба плоскостью

1. Если пересечь куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то в сечении будет квадрат, длина стороны которого будет равна длине ребра куба. Эта плоскость делит куб два равных прямоугольных параллелепипеда.

2. Если пересечь куб с ребром a плоскостью, проходящей через центр куба и два параллельных ребра, то в сечении будет прямоугольник со сторонами a и a√2, площадью сечения a²√2. Эта плоскость делит куб две равные призмы.

3. Если пересечь куб плоскостью, проходящей через центр и середины шести граней, то в сечении будет правильный шестиугольник со стороной a√2/2, площадью сечения a²(3√3)/4. У куба одна из диагоналей (FC) каждой грани, что пересекаются, перпендикулярна стороне шестиугольника.

4. Если пересечь куб плоскостью, проходящей через три вершины куба, то в сечении будет правильный треугольник со стороной a√2, площадью сечения a²√3/2 и объемом большей части — 5a³/6 и меньшей — a³/6. Одна из диагоналей куба (EC) перпендикулярна к плоскости сечения и проходит через центр треугольника (M) и делится плоскостью в отношении MC:EМ = 2:1.

Все таблицы и формулы

Что такое куб: определение, свойства, формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Что такое куб: определение, свойства, формулы

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

• Определение куба
• Свойства куба
  • Свойство 1
  • Свойство 2
  • Свойство 3
• Формулы для куба
  • Диагональ
  • Диагональ грани
  • Площадь полной поверхности
  • Периметр ребер
  • Объем
  • Радиус описанного вокруг шара
  • Радиус вписанного шара

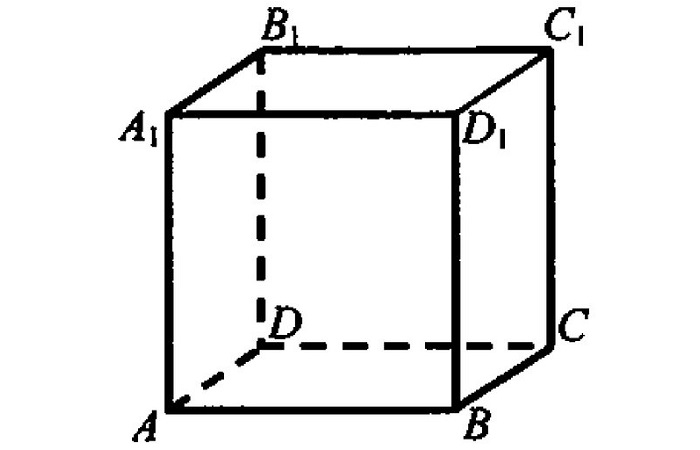
Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

• Вершины куба – это точки, являющиеся вершинами его граней.
  Всего их 8: A, B, C, D, A₁, B₁, C₁ и D₁.
• Ребра куба – это стороны его граней.
  Всего их 12: AB, BC, CD, AD, AA₁, BB₁
  , CC₁, DD₁, A₁B₁, B₁C₁, C₁D₁ и A₁D₁.
• Грани куба – это квадраты, из которого состоит фигура.
  Всего их 6: ABCD, A₁B₁C₁D₁, AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.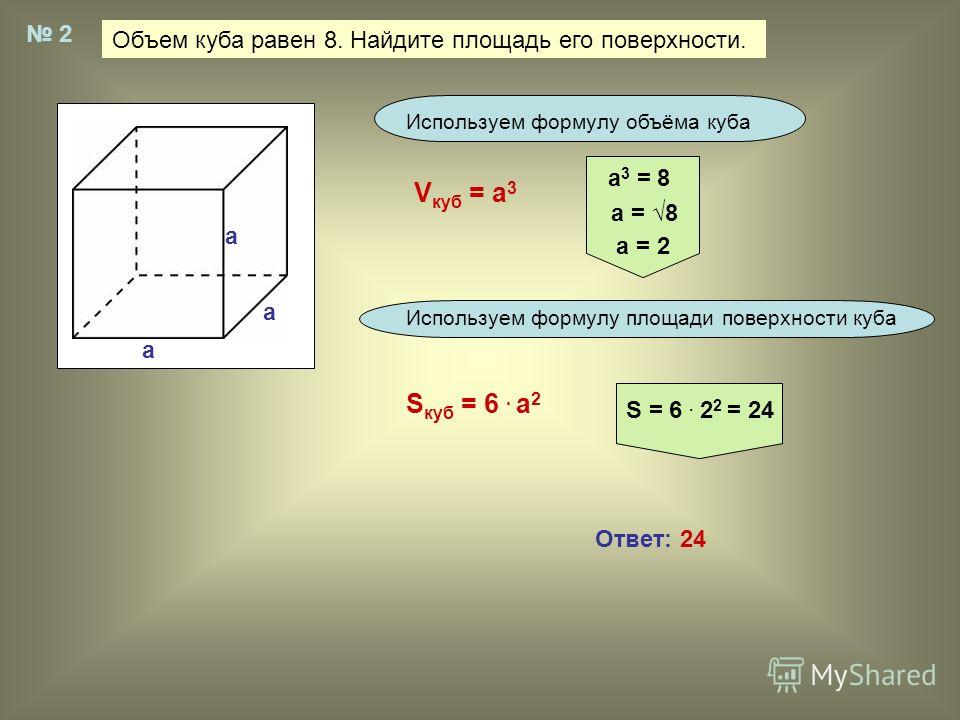 е.:

• ABCD || A₁B₁C₁D₁
• AA₁B₁B || CC₁D₁D
• BB₁C₁C || AA
  ₁D₁D

Свойство 2

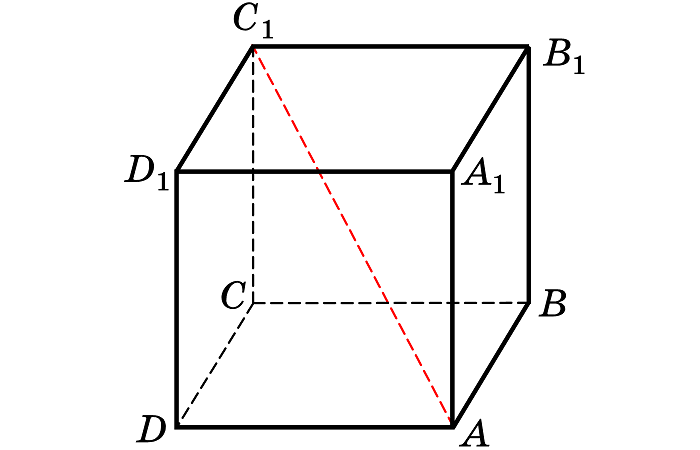
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

• AC₁ = BD₁ = A₁C = B₁D (диагонали куба).
• О – точка пересечения диагоналей:
  AO = OC₁ = BO = OD₁ = A₁O = OC = B₁O = OD.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

• a – ребро куба;
• d – диагональ куба или его грани.

Диагональ

Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.

Диагональ грани

Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

Периметр ребер

Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.

Объем

Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара

Радиус шара, описанного около куба, равняется половине его диагонали.

Радиус вписанного шара

Радиус вписанного в куб шара равен половине длины его ребра.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Куб — свойства, виды и формулы » Kupuk.

net

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

• многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

• прямая призма, все грани которой есть квадраты;

•  прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Элементы куба

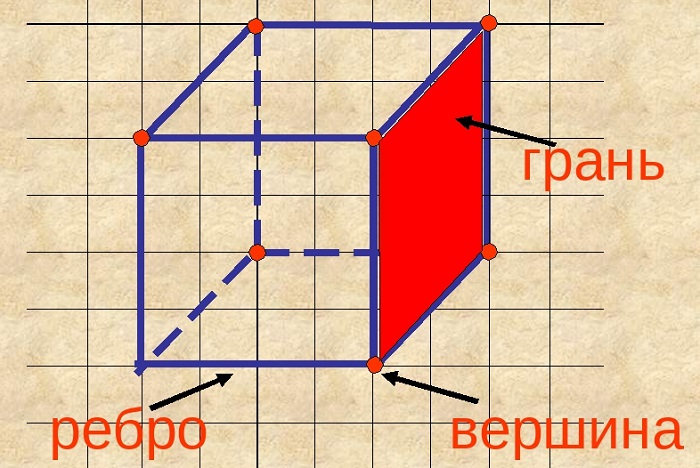
Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю. 

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника. 

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Периметр куба

Сумма длин всех рёбер равна:

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба. 

Радиус равен половине ребра:

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ.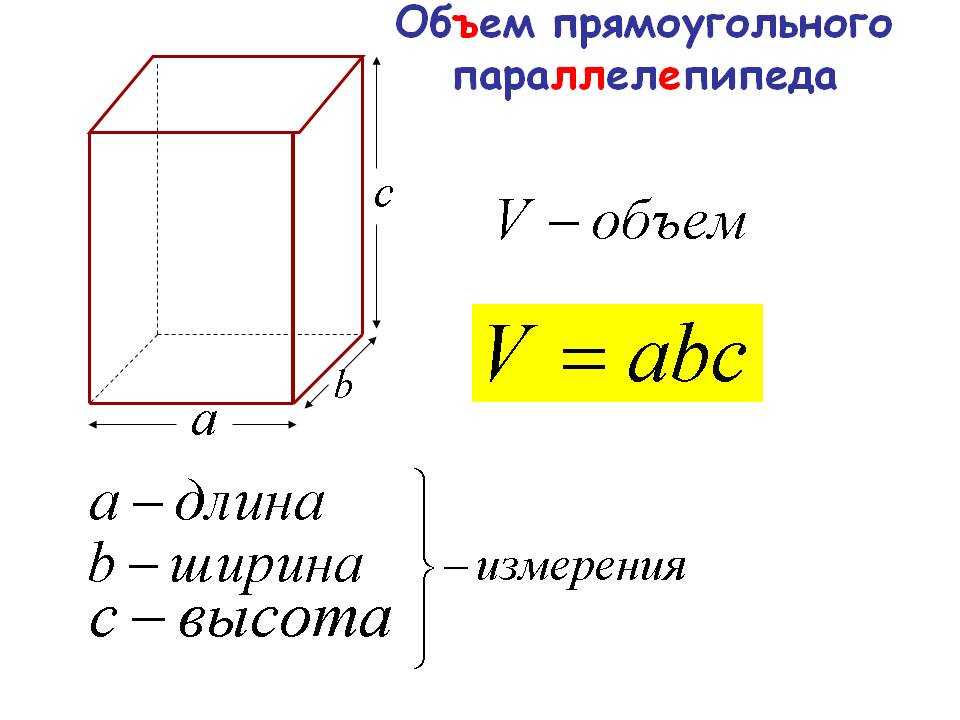 Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

Прочие свойства:

• у куба все грани равны, являются квадратами;

• у куба все рёбра равны;

• один центр и несколько осей симметрии.

Cube Formula — Что такое Cube Formula? Примеры

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.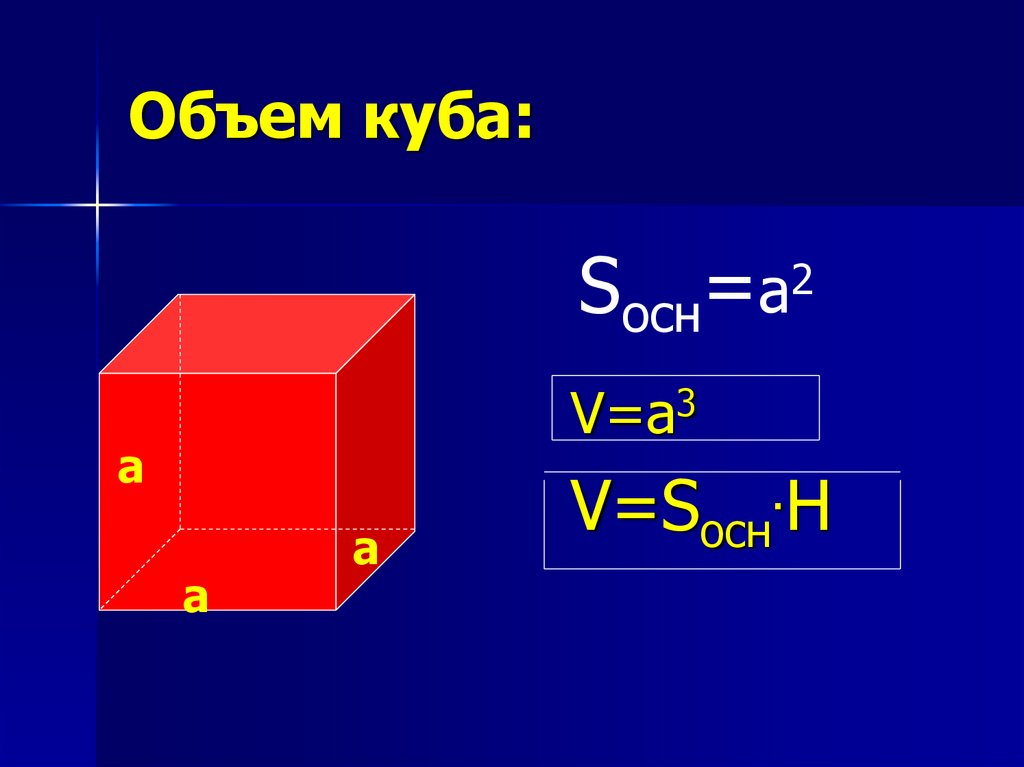 Куб — это трехмерный твердый объект с шестью квадратными гранями, все стороны которого имеют одинаковую длину. Давайте узнаем о формуле куба с несколькими решенными примерами в конце.

Что такое формула куба?

Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.

Формула куба

Объем куба

Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.

• Объем куба (на основе длины стороны) = a ³  кубических дюймов, где a – длина стороны куба
• Объем куба (по диагонали) = (√3×d ³ )/9кубических дюймов, где d — длина диагонали куба

Боковая площадь куба

Боковая площадь куба равна сумме площадей всех боковых граней куба. У куба 4 боковые грани, поэтому сумма площадей всех 4 боковых граней куба равна его боковой поверхности.

LSA куба = 4a ²

, где a — длина стороны.

Общая площадь куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a ²

, где a — длина стороны.

Диагональ куба

Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.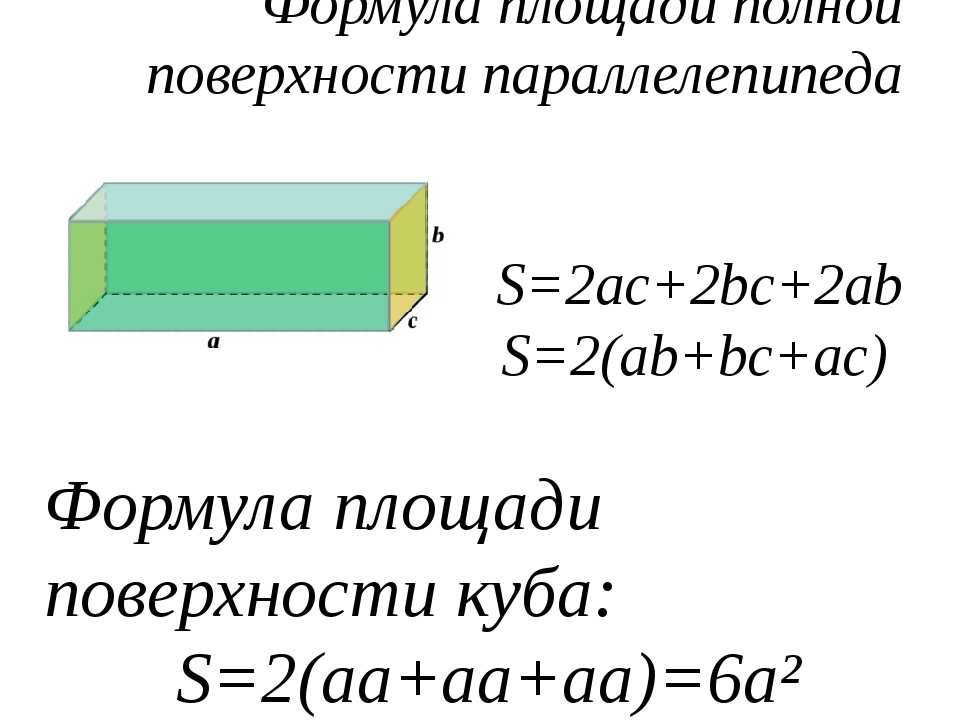

Диагональ куба = a√3

Давайте лучше разберемся с формулами куба на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры с использованием формулы куба

Пример 1: Найдите объем кубика Рубика длиной 4 дюйма.
Решение:

Чтобы найти объем кубика Рубика: кубик Рубика0003

Длина стороны куба = 4 дюйма (дано)

Используя формулу куба,
объем = с × с × с = с ³

Поместите значения,

объем = 4 × 4 × 4 = 4 ³  = 64

Ответ: Объем кубика Рубика составляет 64 кубических дюйма.

Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба.
Решение: 

Чтобы найти диагональ куба:

Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)

Используя формулу куба,

диагональ = a√3 

Поместите значения,

Диагональ = 64√3 = 110,848 дюйма

Ответ: Диагональ куба равна 110,848 дюйма

Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам. . 

Решение:

Длина стороны куба, a = 25 дюймов 

Используя формулу площади куба, а именно: A = 6a ²

Поместите значения,

A = 6 × 25 × 25 = 3750 квадратных дюймов

Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.

Как рассчитать диагональ куба по формуле куба?

Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .

Что такое s в формуле куба?

В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.

Как вывести формулу куба?

Чтобы вычислить объем по формуле куба,

• Шаг 1: Рассмотрим любой квадратный лист бумаги.
• Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s ² ».
• Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».

Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s ²  × s = s ³

Чтобы вывести формулу поверхности куба,

• Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
• Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s ² » (длина, умноженная на ширину).
• Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s ²

Куб – формула, форма, определение, примеры

Куб – это трехмерный объект, имеющий 6 конгруэнтных квадратных граней. Размеры всех 6 квадратных граней куба одинаковы. Куб иногда также называют правильным шестигранником или квадратной призмой. Это одно из 5 платоновых тел. Некоторыми примерами куба из реальной жизни являются кубик льда, кубик Рубика, обычные игральные кости и т. Д. Давайте узнаем о кубе вместе с его формулами, несколькими решенными примерами и практическими вопросами здесь.

1.	Определение куба
2.	Свойства куба
3.	Кубическая сетка
4.	Формула куба
5.	Часто задаваемые вопросы о кубе

Определение куба

Куб — это твердый трехмерный объект с шестью квадратными гранями, все стороны которого имеют одинаковую длину. Он также известен как правильный шестигранник и является одним из пяти платоновых тел. Фигура состоит из шести квадратных граней, восьми вершин и двенадцати ребер. Длина, ширина и высота в кубе имеют одинаковые измерения, поскольку трехмерная фигура представляет собой квадрат, все стороны которого имеют одинаковую длину. В кубе грани имеют общую границу, называемую ребром, которая считается ограничивающей линией ребра. Структура определяется так, что каждая грань соединена с четырьмя вершинами и четырьмя ребрами, вершина связана с тремя ребрами и тремя гранями, а ребра соприкасаются с двумя гранями и двумя вершинами.

Куб Значение

Куб — это объемная объемная фигура, имеющая 6 квадратных граней. Это геометрическая фигура с 6 равными гранями, 8 вершинами и 12 равными ребрами. Некоторые примеры кубиков из реальной жизни — это игра в кости, кубики льда, кубик Рубика и т. д., которые мы видим вокруг себя.

Свойства куба

Куб считается особым видом квадратной призмы, так как все грани имеют форму квадрата и являются платоновыми телами.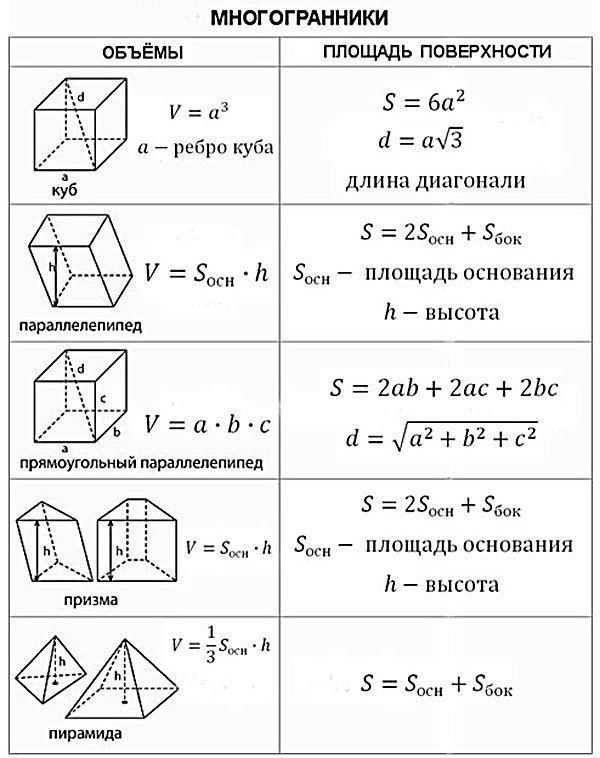 У куба, как и у любой другой трехмерной или двумерной формы, есть множество различных свойств. Свойства:

• Куб имеет 12 ребер, 6 граней и 8 вершин.
• Все грани куба имеют форму квадрата, поэтому длина, ширина и высота одинаковы.
• Углы между любыми двумя гранями или поверхностями равны 90°.
• Противоположные плоскости или грани куба параллельны друг другу.
• Противоположные ребра куба параллельны друг другу.
• Каждая грань куба встречается с остальными четырьмя гранями.
• Каждая вершина куба встречается с тремя гранями и тремя ребрами.

Кубическая сетка

Сетка куба формируется, когда трехмерная фигура с квадратными гранями сглаживается путем разделения по краям, превращая ее в двумерную фигуру. Через сетку куба мы можем ясно видеть шесть граней, то есть шесть квадратных граней, которые соединяются вместе по краям, образуя куб. Вот изображение для справки:

Куб Формула

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Давайте обсудим различные формулы куба.

Площадь поверхности куба

Существует два типа площадей поверхности куба — Площадь боковой поверхности и Общая площадь поверхности

Площадь боковой поверхности куба

Площадь боковой поверхности куба равна сумме площадей всех боковые грани куба. У куба 4 боковые грани, поэтому сумма площадей всех 4 боковых граней куба равна его боковой поверхности. Боковая площадь куба также известна как площадь его боковой поверхности (LSA) и измеряется в квадратных единицах.

LSA куба = 4a ²

, где a — длина стороны. Для получения дополнительной информации вы можете проверить эту интересную статью о боковой площади формулы куба.

Общая площадь поверхности куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз.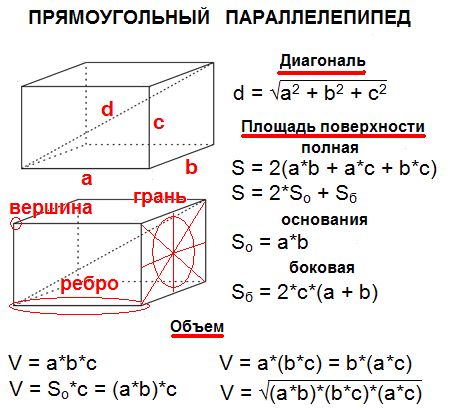 Он измеряется как «количество квадратных единиц» (квадратные сантиметры, квадратные дюймы, квадратные футы и т. д.). Следовательно, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a ²

, где a — длина стороны. Для получения дополнительной информации вы можете ознакомиться с этой интересной статьей о площади поверхности куба.

Объем куба

Объем куба – это пространство, занимаемое кубом. Объем куба можно узнать, найдя куб длины стороны куба. Для определения объема куба существуют разные формулы, основанные на разных параметрах. Его можно рассчитать, используя длину стороны или размер диагонали куба, и он выражается в кубических единицах длины. Следовательно, две разные формулы для нахождения объема куба:

• Объем куба (на основе длины стороны) = a ³ , где a — длина стороны куба
• Объем куба (по диагонали) = (√3×d ³ )/9 , где d — длина диагонали куба

Вы можете узнать больше о формуле объема, прочитав эту интересную статью о объеме куба.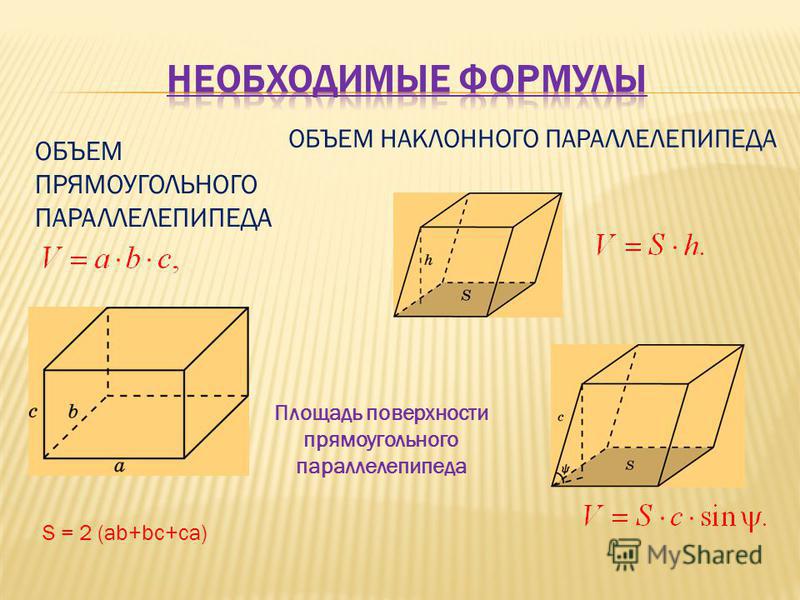

Диагональ куба

Диагональ куба — это отрезок, соединяющий две противоположные вершины куба. Длину диагонали куба можно определить по формуле диагонали куба. Это помогает найти длину диагоналей лица и главных диагоналей. Каждая диагональ грани образует гипотенузу образовавшегося прямоугольного треугольника. Куб имеет шесть граней (квадратной формы). На каждой грани есть две диагонали, соединяющие несмежные вершины. Следовательно, у нас есть двенадцать диагоналей граней и четыре главные диагонали, соединяющие противоположные вершины куба. Формула диагонали куба для расчета длины диагонали грани и диагонали основного тела куба определяется как 9.0003

• Длина диагонали грани куба = √2a единиц , где a = длина каждой стороны куба
• Длина главной диагонали куба = √3a единиц , где a = длина каждой стороны куба

Давайте посмотрим на несколько решенных примеров куба и его свойств для лучшего понимания.

☛Связанные темы

Ниже перечислены некоторые темы, связанные с кубом.

• Куб Формула
• Платоновые тела
• Формы
• Твердые формы
• Плоские фигуры

Примеры кубов

1. Пример 1: Сколько воды хранится в одном кубике льда со стороной 5 дюймов?

   Решение:

   Дано,

   Длина кубика льда = 5 дюймов

   Количество воды в кубике льда = объему кубика

   Следовательно, объем кубика льда = 5 × 5 × 5 в ³

   = 125 в ³

   Ответ: Количество воды во льду равно 125 в

   0 13 900.

2. Пример 2: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.

   Решение:

   Длина стороны куба, a = 25 дюймов формула площади куба: A = 6a ²

   A = 6 × 25 × 25

   A = 3750

   Ответ: Площадь поверхности куба составляет 3750 квадратных дюймов.

3. Пример 3: Найдите объем кубика Рубика длиной 5 дюймов.

   Решение:

   Чтобы найти объем кубика Рубика:

   Длина стороны кубика = 5 дюймов ( дано)

   Используя формулу куба,
   объем = с × с × с = с ³

   Поставьте значения,

   объем = 5 × 5 × 5 = 5 ³ = 125

   Ответ: Объем кубика Рубика равен 125 кубических дюймов.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запись на бесплатный пробный урок

Практические вопросы по Cube

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о Cube

Что такое куб в геометрии?

В геометрии куб представляет собой трехмерную геометрическую фигуру с шестью конгруэнтными квадратными гранями. Идеальным примером куба из реальной жизни является кубик льда. Это одно из пяти платоновых тел, также известное как правильный шестигранник.

Каковы два основных свойства куба?

Куб — это трехмерная фигура со многими геометрическими свойствами. Два основных свойства перечислены ниже.

• Куб имеет 12 ребер, 6 граней и 8 вершин.
• Все грани куба имеют квадратную форму.

Почему куб называют правильным шестигранником?

Правильный шестигранник представляет собой трехмерный объект с 6 конгруэнтными гранями. Таким образом, куб называется правильным шестигранником.

Какая формула площади боковой стороны куба?

Площадь поперечной стороны куба можно вычислить, зная длину его ребра. Площадь боковой стороны куба с длиной ребра ‘x’ равна 4×9.0020 2 кв. шт.

Как найти площадь боковой поверхности куба?

Площадь боковой стороны куба с длиной ребра ‘x’ можно получить, сложив площади 4-х боковых граней. Таким образом, боковая площадь куба = х ² + х ² + х ² + х ² = 4х ² .

В чем разница между площадью поверхности и боковой поверхностью куба?

Площадь поверхности (или) общая площадь поверхности (TSA) куба представляет собой сумму площадей всех граней, тогда как площадь боковой поверхности (LSA) представляет собой только сумму 4 боковых граней куба. Если «x» — длина ребра куба, то

• Общая площадь поверхности (TSA) = 6x ²
• Площадь боковой поверхности (LSA) = 4x ²

Что такое площадь поверхности и площадь?

Обычно термин «площадь» используется для обозначения пространства, ограниченного двухмерным объектом. «Площадь поверхности» используется для представления суммы площадей всех граней трехмерного объекта.

Что такое объем формулы куба?

Объем куба можно рассчитать по длине стороны. Объем куба ³ , где а — длина стороны куба.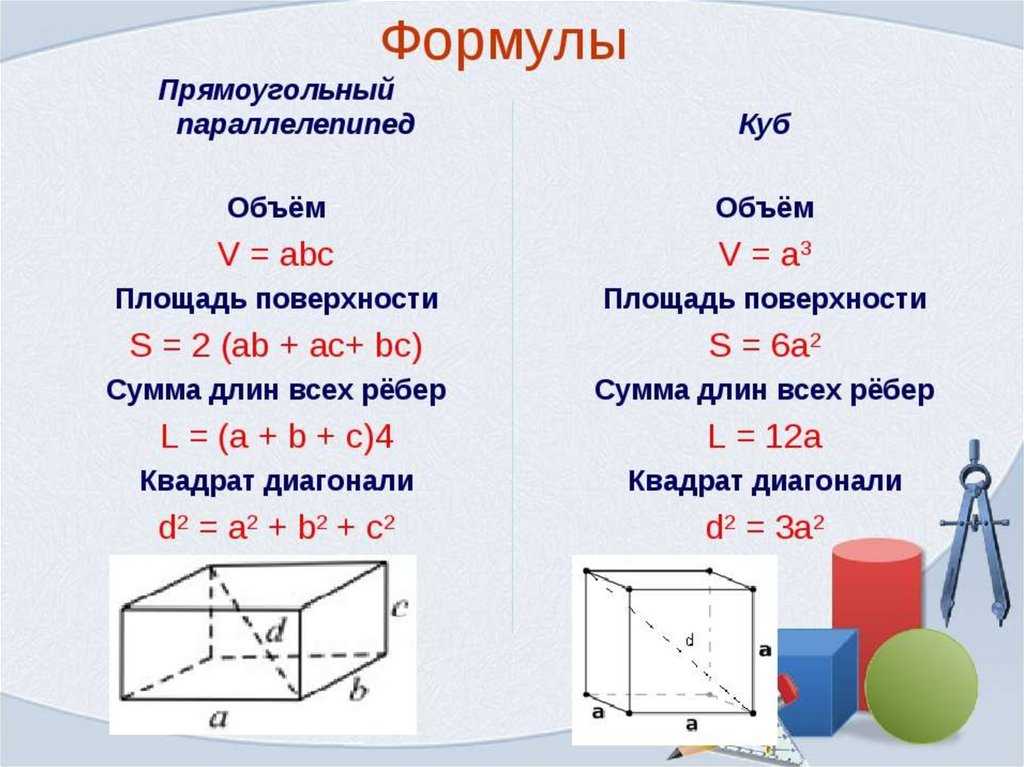

По какой формуле найти площадь основания куба?

Формула для нахождения площади основания куба: ² , где а — длина стороны куба.

Что представляют собой 5 Платоновых тел?

Куб представляет землю, октаэдр представляет воздух, тетраэдр представляет огонь, икосаэдр представляет воду, а додекаэдр представляет вселенную.

Формула куба – объяснение, свойства и примеры решения

Нас окружают разные предметы, которые состоят из разных геометрических форм. Подумайте о детской игре с кубиками, игральными костями или кубиком льда. Что вы замечаете общего среди всего этого? Все они имеют форму куба, не так ли? В этой статье мы изучим, что такое куб? Объем формулы куба, площадь формулы куба, площадь поверхности формулы куба. Некоторыми из распространенных примеров кубика являются кубик льда, игральные кости, кубик Рубика.

Введение. Что такое куб?

Куб — это трехмерная фигура, состоящая из граней квадратной формы одинакового размера. Все углы куба пересекаются в точке 90 ⁰ . У куба 6 равных граней, и все грани квадратной формы. Он имеет 8 вершин и 12 равных ребер.

На приведенном ниже рисунке изображен куб, где l — длина, b — ширина, h — высота, и l = b = h. Длина, ширина и высота представляют ребра куба. И когда три ребра встречаются в точке, это называется вершиной.

(Изображение будет загружено в ближайшее время)

Свойства куба

1.  Все грани куба имеют квадратную форму.

2. Все грани и ребра равны.

3. Углы куба прямые.

4. Каждая из граней встречается с четырьмя соседними гранями.

5. Каждая из вершин встречается с тремя гранями и тремя ребрами.

6. Ребра, противоположные друг другу, параллельны и также равны.

7. Все 12 диагоналей на поверхности имеют площадь одинаковой величины

8. Все 4 внутренние диагонали равны

Площадь поверхности куба Формула площади трехмерный объект. Поскольку трехмерный объект состоит из двухмерных граней, площадь поверхности представляет собой сумму площадей всех граней фигуры. Поэтому, чтобы найти площадь поверхности трехмерного объекта, мы должны сложить площади всех его граней. Мы можем использовать базовую формулу площади для вычисления его граней, поскольку они представляют собой простые 2D-фигуры,

Например, куб имеет шесть граней. Следовательно, площадь его поверхности будет равна сумме площадей всех шести граней. Поскольку все стороны куба являются квадратами, мы можем выразить площадь поверхности куба как 6 x (Площадь квадрата)

В основном площадь поверхности можно классифицировать как:

Площадь изогнутой поверхности объекта – это площадь всех криволинейных поверхностей объекта.

Боковая поверхность предмета – это площадь всех граней предмета, за исключением площади его основания и вершины. Для куба площадь боковой поверхности будет равна сумме площадей четырех сторон, то есть умноженной на 4 стороны.

Площадь боковой поверхности = 4 × (край) 2

902

Куб — это трехмерный объект, поэтому пространство, занимаемое кубом, будет трехмерным.

Куб ограничен шестью квадратными гранями, поэтому площадь поверхности будет вычисляться путем сложения площадей всех шести квадратных граней. Следовательно, площадь поверхности куба по формуле равна 9.0003

Площадь поверхности куба = 6 (сторона) 2

. с точки зрения объема этого объекта. Объем твердого тела является произведением трех измерений, поэтому объем выражается в кубических единицах. Предположим, что объем куба измеряется произведением его длины, ширины и высоты.

Внутренняя часть полого объекта может быть заполнена воздухом или какой-либо жидкостью, которая принимает форму объекта. В таких случаях объем вещества, который может вместить внутренность предмета, называется вместимостью полого предмета. Таким образом, мы можем сказать, что объем объекта — это мера занимаемого им пространства, а вместимость объекта — это объем вещества, которое может вместить его внутренность.

А объем куба — это занимаемое им пространство. Объем формулы куба будет рассчитан как:

Volume = (side) 3

Length of Diagonal of Face of the Cube = √2(edge)

Длина диагонала из куба = √3 (Edge)

3

3

3

9000 9028

3 9000

Периметр = 12 (ребро)

 

Решаемые примеры

Пример 1. Найдите площадь поверхности куба, длина стороны которого равна 7 см.

Решение:

Указанная длина = края = 7 см

Ум.

        = 6 × 49

        =  294 см ²

Пример 2: Сторона кубического ящика равна 9 м. Найдите объем кубического ящика.

Решение:

DED, сторона = A = 9m

по формуле объема A Cube, мы знаем, что

V = A ³ 11963

9

v = ³ 1113

9

v = ³ 1113

9

v = ³ 1113

V = ³ 111996469

v = ³ 11996469

v = ³ 113

V = ^{3 x 9 x 9}

V = 729 кв. м или 729 м ²

Время викторины

1. Каков объем куба 11,5 см?

2. Если объем куба равен 343 см ³ , то какова мера ребра куба?

Значение кубов в математике

Кубы — это трехмерные квадраты, которые многие считают символом геометрического совершенства. С какой стороны на него ни посмотри, он выглядит одинаково. Это часть геометрии в математике и чрезвычайно важна как глава. Понимание этого является ключом к пониманию других связанных концепций. Учащиеся должны быть внимательны при изучении кубиков, так как из этой главы возникнет много вопросов. Они могут перейти к формуле куба — объяснение, свойства и примеры решений и подробно разобраться в этом. На этой странице Веданту каждая концепция упрощена для понимания учеником.