Как найти площадь основания куба?
На этой странице вы найдете ответ на вопрос Как найти площадь основания куба?. Вопрос
соответствует категории Математика и уровню подготовки учащихся 1 – 4 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
Опубликовано 3 года назад по предмету
Математика
от Valeria163
Как найти площадь основания куба?
-
Ответ
Ответ дан
IlyaGordienkoа*а = а²
Длину умножить на ширину.-
Ответ
Ответ дан
Valeria163А что делать,если ребро куба равно 7 дм?
-
Ответ
Ответ дан
IlyaGordienko7 дм * 7 дм = 49 дм (квадратных).
-
Ответ
Ответ дан
Valeria163Спасибо большое,я уже поняла :3
-
Ответ
Ответ дан
IlyaGordienkoНе за что.
-
Самые новые вопросы
![]()
Другие предметы – 2 года назад
Сочинение-рассуждение. прочитайте текст. есть у меня внучка. однажды она говорит: — у веры в субботу день рождения. она
![]()
Другие предметы – 2 года назад
Л.н. толстой. как боролся русский богатырь как сказал иван о своей силе? найдите ответ в тексте. запишите.
![]()
История – 2 года назад
Кто такой мильтиад и какова его роль в победе над персами?
![]()
История – 2 года назад
Какие примеры н. м. карамзин использует для разъяснения пользы новой системы престолонаследия? согласны ли вы с позицией
![]()
География – 2 года назад
Дополните схему. она поможет вам лучше усвоить содержание §1.: 1 что изучает география 2 с помощью чего 3 зачем изучают
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади куба
- 1. Через длину ребра
-
2. Через длину диагонали грани
- Примеры задач
Формула вычисления площади куба
1. Через длину ребра
Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.
S = 6 ⋅ a2

Данная формула получена следующим образом:
- Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
- Площадь каждой грани считается так: S = a ⋅ a = a2.
- Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a2.
2. Через длину диагонали грани
Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.

Это значит, что вычислить площадь поверхности фигуры можно так:
S = 6 ⋅ (d/√2)2
Примеры задач
Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.
Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см)2 = 864 см2.
Задание 2
Площадь поверхности куба равняется 294 см2. Вычислите длину его ребра.
Решение:
Примем ребро куба за a. Из формулы расчета площади следует:![]()
Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.
Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √2)2 = 75 см2.
Площадь поверхности куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности куба
Чтобы посчитать площадь поверхности куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чему равна площадь поверхности куба, если:
длина ребра a =
Sпов =
0
Округление ответа:
Чему равна площадь поверхности куба, если:
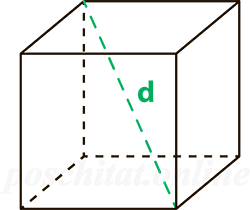
длина диагонали d =
Sпов =
0
Округление ответа:
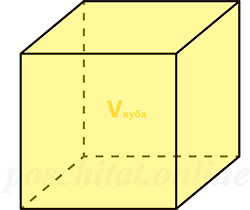
Чему равна площадь поверхности куба, если:
объём Vкуба =
Sпов =
0
Округление ответа:
Теория
Площадь поверхности куба через ребро
Чему равна площадь поверхности куба Sпов, если длина его ребра a:
Формула
Sпов = 6 ⋅ a²
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если он имеет длину рёбер a = 5 см :
Sпов = 6 ⋅ 5² = 6 ⋅ 25 = 150 см²
Площадь поверхности куба через диагональ
Чему равна площадь поверхности куба Sпов, если длина диагонали этого куба d:
Формула
Sпов = 2 ⋅ d²
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если длина диагонали у него d = 3 м:
Sпов = 2 ⋅ 3² = 2 ⋅ 9 = 18 м² = 180 000 см²
Площадь поверхности куба через объем
Чему равна площадь поверхности куба Sпов, если объём куба Vкуба:
Формула
Sпов = 6 ⋅ ³√Vкуба²
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если его объём Vкуба = 8 см³:
Sпов = 6 ⋅ 3√8² = 6 ⋅3√64 = 6 ⋅ 4 = 24 см²
См. также
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
Онлайн-калькулятор площади поверхности куба
У куба есть двенадцать ребер, то есть, отрезков, которые являются сторонами квадратов.
Также он имеет восемь вершин и шесть граней.
У куба есть диагональ, соединяющая противоположные вершины.
Формула площади поверхности куба
Площадь поверхности куба – это сумма площадей всех его граней:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Площадь каждой грани одинакова, то есть:
S1=S2=S3=S4=S5=S6=S′S_1=S_2=S_3=S_4=S_5=S_6=S’
S′S’ — площадь любой грани куба.
Тогда полная площадь поверхности куба запишется как:
S=6⋅S′S=6cdot S’
Рассмотрим на примерах разные способы вычисления полной площади поверхности куба.
Формула площади поверхности куба по длине ребра куба
Площадь каждой грани куба вычисляется как площадь квадрата, со стороной ребра куба по формуле:
S′=a⋅a=a2S’=acdot a=a^2
aa — сторона куба.
Отсюда, окончательно площадь поверхности куба:
S=6⋅a2S=6cdot a^2
aa — длина стороны куба.
Найти площадь поверхности куба, если длина его ребра равна 12 (см.).
Решение
a=12a=12
S=6⋅a2=6⋅122=6⋅144=864S=6cdot a^2=6cdot 12^2=6cdot 144=864 (см. кв.)
Ответ: 864 см. кв.
Формула площади поверхности куба по диагонали куба
По теореме Пифагора, диагональ куба связанна с длиной его ребра по формуле:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
d=3⋅ad=sqrt{3}cdot a
Отсюда:
a=d3a=frac{d}{sqrt{3}}
Подставим в формулу для площади:
S=6⋅a2=6⋅(d3)2=2⋅d2S=6cdot a^2=6cdotBig(frac{d}{sqrt{3}}Big)^2=2cdot d^2
S=2⋅d2S=2cdot d^2
dd — диагональ куба.
Одна четвертая часть диагонали куба равна 2 (см.). Найти площадь поверхности куба.
Решение
14⋅d=2frac{1}{4}cdot d=2
Найдем диагональ:
d=4⋅2=8d=4cdot 2=8
Площадь:
S=2⋅d2=2⋅82=2⋅64=128S=2cdot d^2=2cdot 8^2=2cdot 64=128 (см. кв.)
Ответ: 128 см. кв.
Формула площади поверхности куба по длине диагонали квадрата (грани куба)
По теореме Пифагора, диагональ квадрата ll связанна с его стороной aa:
l2=a2+a2l^2=a^2+a^2
l2=2⋅a2l^2=2cdot a^2
l=2⋅al=sqrt{2}cdot a
Тогда сторона квадрата:
a=l2a=frac{l}{sqrt{2}}
Подставляем в формулу для площади и получаем:
S=6⋅a2=3⋅l2S=6cdot a^2=3cdot l^2
S=3⋅l2S=3cdot l^2
ll — диагональ квадрата (грани куба).
Одна четвертая часть диагонали квадрата равна 1 (см). Найти площадь поверхности куба, образованного данным четырехугольником.
Решение
14⋅l=1frac{1}{4}cdot l=1
Найдем диагональ квадрата:
l=4⋅1=4l=4cdot 1=4
Тогда площадь:
S=3⋅l2=3⋅42=48S=3cdot l^2=3cdot 4^2=48 (см. кв.)
Ответ: 48 см. кв.
Разберем более сложные примеры.
Формула площади поверхности куба по площади вписанного в куб шара
В куб вписан шар площади SшарS_{text{шар}}. Тогда радиус RR этого шара равен половине длины стороны куба aa:
R=a2R=frac{a}{2}
Площадь шара дается формулой:
Sшар=4⋅π⋅R2S_{text{шар}}=4cdotpicdot R^2
Отсюда найдем радиус шара:
R=Sшар4⋅πR=sqrt{frac{S_{text{шар}}}{4cdotpi}}
Сторона грани куба:
a=2⋅R=2⋅Sшар4⋅πa=2cdot R=2cdotsqrt{frac{S_{text{шар}}}{4cdotpi}}
Наконец площадь поверхности куба:
S=6⋅a2=6⋅SшарπS=6cdot a^2=frac{6cdot S_{text{шар}}}{pi}
S=6⋅SшарπS=frac{6cdot S_{text{шар}}}{pi}
SшарS_{text{шар}} — площадь шара, вписанного в куб.
В куб вписан шар, площадь которого равна 64 “пи” (см. кв.). Найти полную площадь поверхности куба.
Решение
Sшар=64πS_{text{шар}}=64pi
По формуле:
S=6⋅Sшарπ=6⋅64⋅ππ=384S=frac{6cdot S_{text{шар}}}{pi}=frac{6cdot 64cdotpi}{pi}=384 (см. кв.)
Ответ: 384 см. кв.
Не знаете, кто сможет решить контрольную работу на заказ для вас? Наши эксперты с удовольствием окажут вам помощь!
